. Darlene is collecting prize tickets. The equation y = 2x + 1 describes the relationship betweenthe number of days (x) since she began collecting and the number of prize tickets (y) she hascollected. Which statement correctly describes a solution of the equation?A. Darlene has collected 2 prize tickets at the end of 1 day.B. Darlene has collected 4 prize tickets at the end of 9 days.C. Darlene has collected 22 prize tickets at the end of 10 days.D. Darlene has collected 25 prize tickets at the end of 12 days.
Answers
SOLUTION:
Darlene is collecting prize tickets.
The equation y = 2x + 1 describes the relationship between the number of days (x) since she began collecting and the number of prize tickets (y) she has
collected.
Which statement correctly describes a solution of the equation?
Darlene has collected 25 prize tickets at the end of 12 days - OPTION D
\(\begin{gathered} Given\text{ that y = 2 x + 1} \\ where\text{ x = the number of days} \\ \text{and y = the number of prize tickets} \end{gathered}\)\(undefined\)Related Questions
16
Find the exact value of x
X =
30
Do the side lengths form a Pythagorean triple?
O Yes
O No
Answers
The exact value of x is √1156 and it follows the Pythagorean triple
Finding the exact value of xFrom the question, we have the following parameters that can be used in our computation:
Legs of the right triangle = 16 and 30
Using the pythagoras theorem, we have
Hypotenuse^2 = the sum of the squares of the other lengths
So, we have
x^2 = 16^2 + 30^2
When evaluated, we have
x^2 = 1156
This gives
x = √1156
Hence, the exact value is √1156
Read more about pythagoras theorem at
https://brainly.com/question/231802
#SPJ1
Given f(x) = -* -
- 5, solve for x when f(x) = -3.

Answers
Answer:
x = -2
Step-by-step explanation:
Step 1: Define
f(x) = -x - 5
f(x) = -3
Step 2: Substitute and Evaluate
-3 = -x - 5
2 = -x
x = -2
e
3. If y varies inversely as the square of x and x = 6 when y = -18
find y when x = 8
Answers
The calculated value of y when x = 8 is 10.125
Finding the value of y when x = 8From the question, we have the following parameters that can be used in our computation:
y varies inversely as the square of x
Mathematically, this can be expressed as
y = k/x²
So, we have
k = x²y
Given that x = 6 when y = -18, we have
k = 6² * -18
So, we have
k = -648
When x = 8, we have
y = -648/8²
Evaluate
y = -10.125
Hence, the value of y is 10.125
Read more about variation at
https://brainly.com/question/6499629
#SPJ1
When a new machine is functioning properly, only 3% of the items produced are defective.
Assume that we will randomly select two parts produced on the machine and that we are
interested in the number of defective parts found.
a. Describe the conditions under which this situation would be a binomial experiment.
b. Draw a tree diagram similar to Figure 5.3 showing this problem as a two-trial experiment.
c. How many experimental outcomes result in exactly one defect being found?
d. Compute the probabilities associated with finding no defects, exactly one defect, and
two defects.
Answers
a. This situation would be a binomial experiment if the following conditions are met:
The trials are independent: The selection of one part does not affect the selection of the other.
Each trial has two possible outcomes: In this case, defective or non-defective.
The probability of success (finding a defective part) remains constant for each trial: In this case, the probability is 3% or 0.03.
The number of trials is fixed: We are selecting two parts, so the number of trials is predetermined.
b. Here is a tree diagram representing the two-trial experiment:
D ND
/ \ / \
D ND D ND
The branches represent the two trials, with D representing a defective part and ND representing a non-defective part.
c. To find the number of experimental outcomes resulting in exactly one defect, we can observe that there are two outcomes that meet this criterion: D-ND and ND-D. Both represent one defective part and one non-defective part.
d. The probabilities associated with finding no defects, exactly one defect, and two defects can be calculated as follows:
Probability of finding no defects: (1 - probability of finding a defective part) * (1 - probability of finding a defective part) = (1 - 0.03) * (1 - 0.03) = 0.97 * 0.97 = 0.9409.
Probability of finding exactly one defect: (probability of finding a defective part) * (probability of finding a non-defective part) + (probability of finding a non-defective part) * (probability of finding a defective part) = 0.03 * 0.97 + 0.97 * 0.03 = 0.0582.
Probability of finding two defects: (probability of finding a defective part) * (probability of finding a defective part) = 0.03 * 0.03 = 0.0009.
Therefore, the probabilities associated with finding no defects, exactly one defect, and two defects are approximately 0.9409, 0.0582, and 0.0009, respectively.
for more such questions on binomial experiment
https://brainly.com/question/28941825
#SPJ8
Could I please get help on this word problem answer 13
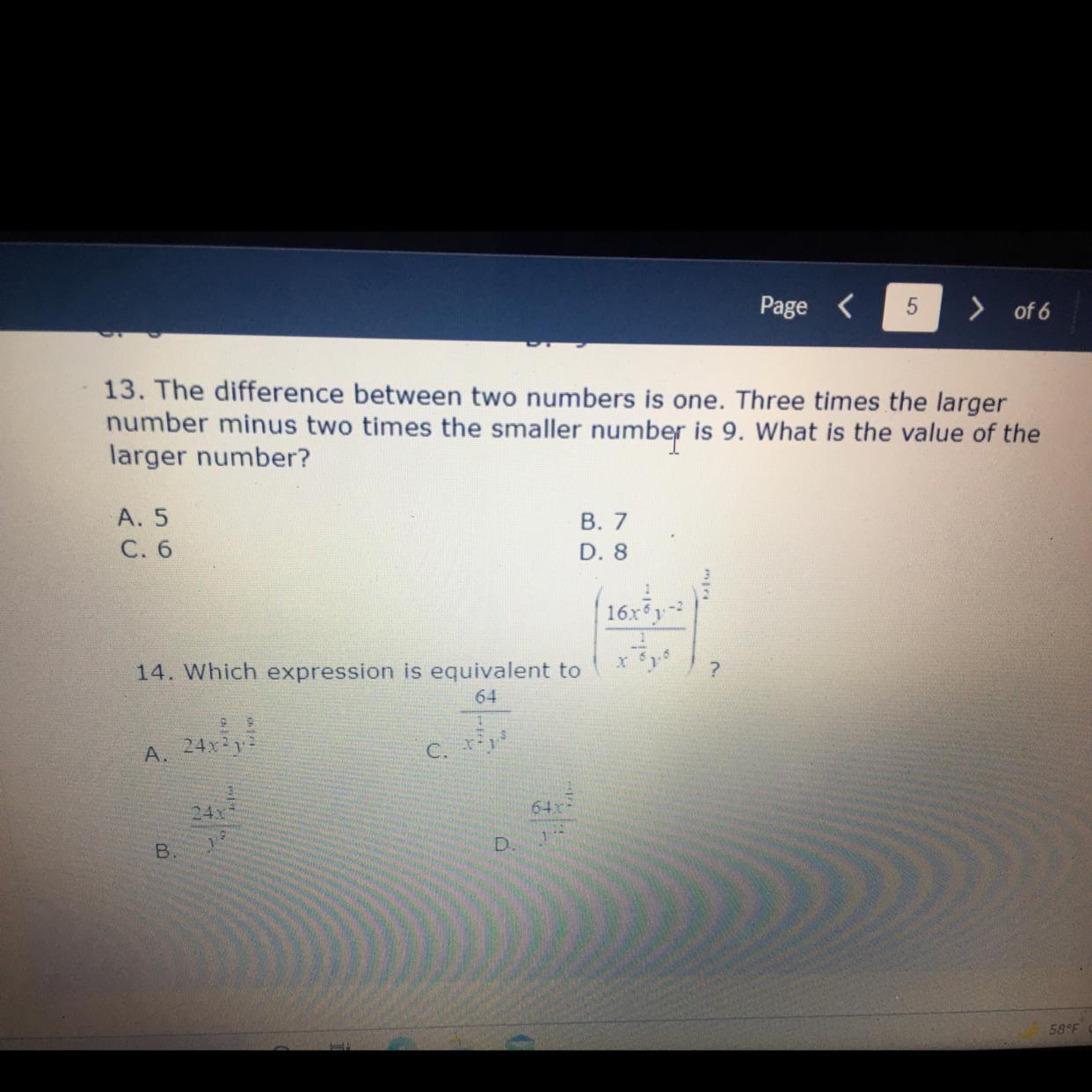
Answers
Let y = the larger number; and x = the smaler number.
Step 1.
Set up a system of equations:
y - x = 1 eq. 1
3y - 2x = 9 eq 2.
Step 2.
Solve the system by elimination:
1. Multiply eq. 1. by -3:
-3y + 3x = - 3 eq 3.
2. Subtract eq. 2. from eq. 3.:
-3y + 3x = - 3
3y - 2x = 9
_____________
x = 6
3. Substituting x = 6 on eq. 1:
y - x = 1
y - 6 = 1
y = 7
Answer: The larger number is 7.
Cindy is designing a rectangular fountain in the middle of a courtyard. The rest of the courtyard will be covered in stone.The part of the courtyard that will be covered in stone has an area of 246 square feet. What fraction of the area of the courtyard will be occupied by the fouantain.
Answers
The fountain will occupy a fraction of 50/173 of the Total area of the courtyard.
Let A be the area of the courtyard and F be the area of the fountain.
We know that the area of the stone-covered part of the courtyard is 246 square feet.
So, the area of the whole courtyard is A = 246 + F square feet.
The fraction of the area of the courtyard occupied by the fountain is given by:
F / A = F / (246 + F)
We can simplify this expression by multiplying the numerator and denominator by the reciprocal of the denominator:
F / A = F / (246 + F) * (1 / (246 + F))
F / A = F / (246 * (246 + F))
F / A = 1 / (246 / F + 1)
We don't know F yet, but we can use the fact that the fountain is rectangular to set up an equation relating the length and width of the fountain:
F = L * W
where L is the length of the fountain and W is the width of the fountain.
We also know that the perimeter of the fountain is 50 feet:
2L + 2W = 50
Simplifying this equation, we get:
L + W = 25
Solving for one variable in terms of the other, we get:
L = 25 - W
Substituting this expression for L into the equation for F, we get:
F = (25 - W) * W
Expanding this expression, we get:
F = 25W - W^2
We also know that the cost of the fountain is $600, which includes installation. So, we can set up another equation relating the cost of the fountain to its dimensions:
1.5LW = 600
Substituting 25 - W for L, we get:
1.5(25 - W)W = 600
Expanding and simplifying this equation, we get:
W^2 - 25W + 400 = 0
Solving this quadratic equation, we get:
W = 20 or W = 5
We reject the solution W = 5 because it implies a negative length for the fountain, which is not physically possible. Therefore, the width of the fountain is W = 20 feet and its length is L = 25 - W = 5 feet.
The area of the fountain is therefore:
F = L * W = 5 * 20 = 100 square feet
The fraction of the area of the courtyard occupied by the fountain is
F / A = 100 / (246 + 100) = 100 / 346 = 50 / 173
So, the fountain will occupy a fraction of 50/173 of the total area of the courtyard.
To know more about Total area.
https://brainly.com/question/884576
#SPJ11
Based on Milton Friedman's observations, it is likely that he would agree that socialism provides the best government for which a free market can exist.
Please select the best answer from the choices provided
T
F
Answers
Answer:
False
Step-by-step explanation:
I did the E2020 assignment
5 times 100 times 105
Answers
Answer:
52500
Step-by-step explanation:
first do 5*105 to get 525 then mutiply by 100 to get 52500
Which is the equation of a line that has a slope of 1 and passes through point (5, 3)?
y = -2
y = x + 2
y = x + 3
y=x-5
Answers
Answer:
y = x - 2
Step-by-step explanation:
y = x + b
3 = 5 + b
y = x - 2
We can use the slope intercept form of a line.
y = mx+b where m is the slope and b is the y intercept
y = 1x +b
Substitute the point into the equation
3 = 1*5+b
3 = 5+b
Subtract 5 from each side
3-5 = 5+b-5
-2 =b
y = x-2
If 12Kg of chicken feed cost 20 how much would 5kg cost?
and what is the unit rate? ( price per 1 kg)
Answers
Step-by-step explanation:
if you 12kg cost 20 what about 5kg that will be 5kg×20÷12kg= 8.33 when you round of to the nearest hundredth this is the price of 5kg
sorry but i dont think i know how to answer the other question i have done what i only know thankyou
What is the sin B?
/21
B
5
2
sin (B) =
[?]
![What is the sin B?/21B52sin (B) =[?]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/bJqEBQdNtkeNzRPqszdQkxPqXUYlMPak.png)
Answers
Answer:
Step-by-step explanation:
sin (B) = \(\frac{2}{5}\)
Find f. (Use C for the constant of the first antiderivative and D for the constant of the second antiderivative.)
f ''(x) = 2x + 4ex
Answers
After integration, the required function f is (2x³ - sin (x) + Cx + D).
What is the integration of 'xⁿ' and 'sin (x)'?
\(\int {x^{n} } \, dx = \frac{x^{n+1} }{n+1} + C\\\\\\\int {sinx} \, dx = -cosx + C\)
Given, f''(x) = 12x + sin x
Therefore,
\(\int {f''(x)} \, dx \\\\=\int {f'(x)} \, dx \\\\\\= \int{12x + sin x} \, dx + C\\\\= 6x^{2} - cosx + C\\\)
Again, f'(x) = 6x - cos (x) + C
Therefore,
\(\int {f'(x)} \, dx\\ \\=\int {f(x)} \, dx \\\\= \int {6x^{2} - cosx + C } \, dx \\\\= 2x^{3} - sinx + Cx + D\)
Therefore, the required function is (2x³ - sin (x) + Cx + D).
Learn more about integration at:
brainly.com/question/17072971
#SPJ4
Angle α lies in quadrant II, and tanα=−12/5. Angle β lies in quadrant IV, and cosβ=35.
What is the exact value of cos(α+β)?
Enter your answer in the box.

Answers
Answer:
Step-by-step explanation:
[-5/13] 3/5 +12+13 [-4/5 = - 63/65
Help ASAP PLSSS!! I’d really appreciate it! Thank youuu!

Answers
C = 180 - (80 + 45)
C = 180 - 125
C = 55
I teach geometry :)
Identify the property demonstrated.
4(3+5) = 4.3 +4.5
-associative property of
multiplication
-commutative property of multiplication
-distributive property
-identity property of multiplication
Answers
Answer:
Distributive property
Step-by-step explanation:
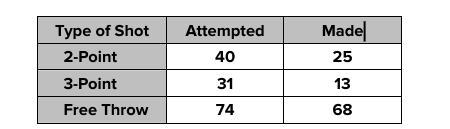
Evan is looking at his shot chart and is curious whether he will reach 200 points during the regular season. There are only three regular season games left. Based on his shot chart, will he statistically be able to hit this milestone if he attempts five of each type of shot per game? How many points is he likely to have at the end of the season based on his shot chart. (Free throws are worth 1 point each.)
Answers
Evan is likely to have 247 points at the end of the regular season. He will surpass the 200-point milestone.
To determine if Evan will reach 200 points during the regular season, we need to calculate the number of points he can potentially score in the remaining three games.
Given his shot chart:
2-Point attempts: 40
2-Point made: 25
3-Point attempts: 31
3-Point made: 13
Free throw attempts: 74
The free throw made: 68
First, let's calculate the total points Evan has scored so far:
2-Point made: 25 * 2 = 50 points
3-Point made: 13 * 3 = 39 points
The free throw made: 68 * 1 = 68 points
Total points scored so far: 50 + 39 + 68 = 157 points
Now, let's calculate the maximum number of points Evan can potentially score in the remaining three games:
2-Point attempts:
3 games * 5 attempts/game * 2 points/attempt = 30 points
3-Point attempts:
3 games * 5 attempts/game * 3 points/attempt = 45 points
Free throw attempts:
3 games * 5 attempts/game * 1 point/attempt = 15 points
Total potential points in the remaining three games:
30 + 45 + 15 = 90 points
Finally, let's calculate the projected total points for the season:
Total points scored so far: 157 points
Total potential points in the remaining three games: 90 points
Projected total points for the season: 157 + 90 = 247 points
Based on his shot chart and the given attempts per game, Evan is likely to have 247 points at the end of the regular season. He will surpass the 200-point milestone.
Learn more about Free Throw:
https://brainly.com/question/30804832
#SPJ1
Please Help! Multiple Choice


Answers
Using the z-distribution, the z-statistic would be given as follows:
c) z = -2.63.
What are the hypothesis tested?At the null hypothesis we test if the means are equal, hence:
\(H_0: \mu_D - \mu_C = 0\)
At the alternative hypothesis, it is tested if they are different, hence:
\(H_1: \mu_D - \mu_C \neq 0\)
What are the mean and the standard error for the distribution of differences?For each sample, they are given as follows:
\(\mu_D = 12, s_D = \frac{5.2}{\sqrt{73}} = 0.6086\)\(\mu_C = 14, s_C = \frac{4.1}{\sqrt{81}} = 0.4556\)Hence, for the distribution of differences, they are given by:
\(\overline{x} = 12 - 14 = -2\).\(s = \sqrt{0.6086^2 + 0.4556^2} = 0.76\)What is the test statistic?The test statistic is given by:
\(z = \frac{\overline{x} - \mu}{s}\)
In which \(\mu = 0\) is the value tested at the null hypothesis.
Hence:
\(z = \frac{\overline{x} - \mu}{s}\)
\(z = \frac{-2 - 0}{0.76}\)
z = -2.63.
Hence option B is correct.
More can be learned about the z-distribution at brainly.com/question/13873630
#SPJ1
Which technique for sampling 20 tosses of a coin would most likely introduce a sampling error?
Choosing the first 10 events for the sample
Putting all the events into two groups of heads and tails and randomly selecting 5 events from each group
Numbering all the events and using a random number generator to select 10 events
Taking every other event until 10 events are selected
Answers
The sampling that would most likely introduce a sampling error is (a) Choosing the first 10 events for the sample
Selecting the sampling that would most likely introduce a sampling error?
From the question, we have the following parameters that can be used in our computation:
The list of options
Also, we have
Tosses = 20
From the list of options, we have
(a) Choosing the first 10 events for the sample
This techique will introduce a sampling error because the selection done by the sampling is not a random selection
Read more about sampling technique at
https://brainly.com/question/11765786
#SPJ1
Can someone answer theese 3 questions
Answers
Answer:
Which three questions?
Step-by-step explanation:
I've answered this first question, I guess I need two more...
which of the following is most likely the next step in the series

Answers
Answer:
A.
Step-by-step explanation:
Let's think of this as a clock. We can see that the 2 lines start in the same place, around 3 o'clock. Next, one of the line segments shifts down to around 6 o'clock. Next, it shifts to about 9 o'clock. Logically, the next step (in a clock) would be 12 o'clock, making A the correct choice.
We can also just use a regular circle, with one of the line segments moving 90 degrees each time.
Hope this helps! :)
PV = $250,000 / (1+0.065)^1 + $37,500 / (1+0.065)^2 + $180,000 / (1+0.065)^3 + $300,000 / (1+0.065)^4 + $750,000 / (1+0.065)^5 + $725,000 / (1+0.065)^6
Answers
The given expression represents the present value of a series of future cash flows discounted at a rate of 6.5% per year.
Each term in the expression represents a cash flow at a specific time in the future, and the denominator in each term represents the discount factor, which reflects the time value of money.
The first term, $250,000 / (1+0.065)^1, represents a cash flow of $250,000 that will be received in one year.
To determine its present value, we divide it by the discount factor (1+0.065)^1, which reflects the fact that the money will be received one year from now and is, therefore, less valuable than money received today.
Similarly, the second term, $37,500 / (1+0.065)², represents a cash flow of $37,500 that will be received in two years.
To determine its present value, we divide it by the discount factor (1+0.065)²,
which reflects the fact that the money will be received two years from now and is, therefore, less valuable than money received today.
This process is repeated for each term in the expression, representing cash flows that will be received in three, four, five, and six years, respectively.
The sum of these present values represents the total present value of the cash flows or the amount that they are worth today if they are discounted at a rate of 6.5% per year.
Learn more about Simplification here:
https://brainly.com/question/28996879
#SPJ1
shawn deposits $100 every year into a savings account that pays interest at a rate of 3.5% per year, compounded annually. How much money will there be in his account at the end of 2 years
A-214.25
B-210.62
C-207
D-270
Answers
There will be $210.62 in Shawn's savings account at the end of 2 years, hence, option B is correct.
Using the compound interest formula,
A = P(1 + r)ⁿ where amount of money is A in the account after n years, principal (initial deposit) is P, interest rate per year (as a decimal) is r, and number of years is n. In this case, P = $100, r = 0.035, and n = 2. Plugging these values into the formula, we get,
A = $100(1 + 0.035)²
A = $100(1.072225)
A = $107.22
Therefore, Shawn will have $107.22 in his account at the end of 2 years, which is closest to option B-210.62 (if we assume the deposit is made at the end of each year).
To know more about compound interest, visit,
https://brainly.com/question/28020457
#SPJ1
Jason works for a car dealer and his commission for selling a car is 2% of the selling price. Jason sold two cars last month for $70,000 and $60,000. how much commission in total did Jason receive?
Answers
Answer:
$2600
Step-by-step explanation:
2/100×70000=1400
2/100×60000=1200
1400+1200=2600
A giant tortoise moves at a slow but steady pace. It takes
the giant tortoise 3 seconds to travel 10.5 inches.
How many inches will the tortoise travel in 1 second?
Answers
Select the correct answer.
What is the solution to this equation?
g^x-1=2
A. -1/2
B. 1/2
C. 2
D. 1
Answers
9514 1404 393
Answer:
B. 1/2
Step-by-step explanation:
Maybe you want the solution to ...
\(9^x-1=2\)
You can use logarithms, or your knowledge of powers of 3 to solve this.
\(9^x=3\qquad\text{add 1}\\\\3^{2x}=3^1\qquad\text{express as powers of 3}\\\\2x=1\qquad\text{equate exponents of the same base}\\\\\boxed{x=\dfrac{1}{2}}\qquad\text{divide by 2}\)
Using logarithms, the solution looks like ...
\(x\cdot\log{9}=\log{3}\\\\x=\dfrac{\log{3}}{\log{9}}=\dfrac{1}{2}\)
P=130t+17800 gives the total population, P, of a small city t years after 1951. Use the equation to determine when (what year) the population reached a population of 19880 people.
The population reached a total of 19880 people in what year?
Answers
Answer:
The population reached a total of 19880 people in 1967.
Step-by-step explanation:
The population in t years after 1951 is given by:
\(P(t) = 130t + 17800\)
Which year the population reached a population of 19880 people.
This is t years after 1951
t is found when \(P(t) = 19880\)
So
\(P(t) = 130t + 17800\)
\(19880 = 130t + 17800\)
\(130t = 2080\)
\(t = \frac{2080}{130}\)
\(t = 16\)
1951 + 16 = 1967
The population reached a total of 19880 people in 1967.
If 1 lb = 2 cups what does 1/2 cups equal?
PLEASE HELP
Answers
Answer:
16 ounces equals one pound or two cups. Another way to look at the equivalent is that one cup weighs eight ounces and therefore two cups equal 16 ounces and this is the same weight of one pound--16 ounces.
Step-by-step explanation:
Iron-deficiency anemia is an important nutritional health problem in the United States. A dietary assessment was performed on 51 boys 9 to 11 years of age whose families were below the poverty level. The mean daily iron intake among these boys was found to be 12.50 mg with standard deviation 4.75 mg. Suppose the mean daily iron intake among a large population of 9- to 11-year-old boys from all income strata is 14.44 mg. We want to test whether the mean iron intake among the low-income group is lower than that of the general population.
(a) State the hypotheses that we can use to consider this question.
(b) Carry out the hypothesis test in (a) using the critical-value method with a significance level of .05, and summarize your findings.
(c) What is the p-value for the test conducted in (b)?
(d) The standard deviation of daily iron intake in the larger population of 9- to 11-year-old boys was 5.56 mg. We want to test whether the standard deviation from the low-income group is lower than that of the general population. State the hypotheses that we can use to answer this question.
(e) Carry out the test in (d) and report the p-value with an α level of .05, and summarize your findings.
Answers
Answer:
The null hypothesis is that the mean daily iron intake of the low-income group is equal to or greater than the general population, and the alternative hypothesis is that the mean daily iron intake of the low-income group is less than that of the general population.
H0: μ >= 14.44
Ha: μ < 14.44
(b) We can use a one-tailed t-test to test this hypothesis. With a sample size of 51, degrees of freedom of 50, a sample mean of 12.50, a population mean of 14.44, and a standard deviation of 4.75, we can calculate the t-statistic as follows:
t = (12.50 - 14.44) / (4.75 / sqrt(51)) = -3.16
Using a t-distribution table with 50 degrees of freedom and a significance level of .05, the critical value is -1.677. Since the calculated t-statistic is less than the critical value, we reject the null hypothesis.
Therefore, we can conclude that the mean daily iron intake among the low-income group is significantly lower than that of the general population at a significance level of .05.
(c) The p-value for this test is the probability of obtaining a t-value of -3.16 or more extreme assuming the null hypothesis is true. Using a t-distribution table with 50 degrees of freedom, we find the p-value to be less than .005.
(d) The null hypothesis is that the standard deviation of the low-income group is equal to or greater than that of the general population, and the alternative hypothesis is that the standard deviation of the low-income group is less than that of the general population.
H0: σ >= 5.56
Ha: σ < 5.56
(e) We can use a chi-square test to test this hypothesis. With a sample size of 51, degrees of freedom of 50, and a sample standard deviation of 4.75, we can calculate the chi-square statistic as follows:
chi-square = (n - 1) * s^2 / σ^2 = 50 * 4.75^2 / 5.56^2 = 39.70
Using a chi-square distribution table with 50 degrees of freedom and a significance level of .05, the critical value is 68.67. Since the calculated chi-square statistic is less than the critical value, we fail to reject the null hypothesis.
Therefore, we do not have sufficient evidence to conclude that the standard deviation of daily iron intake among the low-income group is significantly lower than that of the general population at a significance level of .05.
For the payoff matrix shown, find the optimal row and column strategy and the expected value of the game. P = 3 -1
-5 2
Answers
The optimal row strategy = (7/11, 8/11)
the optimal column strategy = \(\begin{bmatrix}\frac{3}{11} \\\\\frac{5}{11}\end{bmatrix}\)
and the expected value of the game = 1/11
Let the row player be R and the column player be C.
We know that the expected value of R’s payoff is given by,
\(\begin{bmatrix}p & 1-p\end{bmatrix} \begin{bmatrix}3 & -1 \\-5 & 2 \end{bmatrix} \begin{bmatrix}q\\1-q\end{bmatrix}\\\\=\begin{bmatrix}3p-5+5p & -p+2-2p\end{bmatrix}\begin{bmatrix}q\\1-q\end{bmatrix}\\\\=\begin{bmatrix}8p-5 & -3p+2\end{bmatrix}\begin{bmatrix}q\\1-q\end{bmatrix}\)
= (8p - 5)q + (-3p + 2)(1 - q)
= 8pq - 5q - 3p + 2 + 3pq - 2q
= 2 + 11pq - 3p - 7q
= 1/11 + 11 (p - 7/11)(q - 3/11)
If R sets p equal to 7/11, then R is guaranteed an expected payoff of 1/11.
If R chooses any other value of p, C can choose a value of q that will make the expression 11 (p - 7/11)(q - 3/11) negative giving a payoff
for R which is less than 1/11.
If R sets p < 7/11 then the expression 11 (p - 7/11)(q - 3/11) is negative as long as q > 3/11.
If p > 7/11 then the expression 11 (p - 7/11)(q - 3/11) is negative as long as q < 3/11.
An expected payoff of 1/11 is the best that R can do if C uses an optimal counterstrategy.
Thus, R’s optimal mixed strategy is (7/11, 8/11)
Similarly C’s best counterstrategy is to set q equal to 3/11 since otherwise R can choose a value of p making the expression 11 (p - 7/11)(q - 3/11) positive to give an expected payoff for R that is greater than 1/11 (thus a payoff for C which is less than -1/11).
Thus C’s optimal strategy is given by \(\begin{bmatrix}\frac{3}{11} \\\\\frac{5}{11}\end{bmatrix}\)
Since the expected pay-off is given by 1/11 + 11 (p - 7/11)(q - 3/11), the value of the game is given by ν = 1/11
Learn more about the matrix here:
https://brainly.com/question/30389982
#SPJ4
Triangle ABC has vertices at A(−3, 3), B(0, 7), and C(−3, 0). Determine the coordinates of the vertices for the image if the preimage is translated 3 units up.
A′(−3, 0), B′(0, 4), C′(−3, −3)
A′(−3, 6), B′(0, 10), C′(−3, 3)
A′(−6, 3), B′(−3, 7), C′(0, 0)
A′(0, 3), B′(3, 5), C′(0, 0)
Answers
Answer:
To translate triangle ABC 3 units up, we need to add 3 to the y-coordinate of each vertex:
A' = (-3, 3 + 3) = (-3, 6)
B' = (0, 7 + 3) = (0, 10)
C' = (-3, 0 + 3) = (-3, 3)
Therefore, the coordinates of the vertices for the image triangle A'B'C' are A'(-3, 6), B'(0, 10), and C'(-3, 3).
So the correct answer is: A′(−3, 6), B′(0, 10), C′(−3, 3).