D) 7 Q 15. What is the limit of: f(x) = 3x3 + 2x2 as x approaches 5? (B) lim f(x) = 452 - 5 5 (A) lim f(x) = 425 (C) lim f(x) = 542 (D) lim f(x) = 245 5 X-5 Q 16. Evaluate the limit: lim, f() where f(x) = {-x2 1, x < 0 + 4x - 3, x>0 - x+ (A) 1 (B) 0 (C) -3 (D) Does not exist
Answers
The left-hand limit and right-hand limit are not equal, the limit of f(x) as x approaches 0 does not exist. So the correct answer is (D).
To find the limit of f(x) = 3x^3 + 2x^2 as x approaches 5, we can simply plug in 5 for x and evaluate the expression:
f(5) = 3(5)^3 + 2(5)^2 = 375 + 50 = 425
Therefore, the limit of f(x) as x approaches 5 is 425. So the correct answer is (A).
To evaluate the limit of f(x) where f(x) = {-x^2 + 1, x < 0; + 4x - 3, x > 0; -x, x = 0}, we need to find the left-hand limit and right-hand limit separately and then check if they are equal.
Left-hand limit:
lim x→0- {-x^2 + 1} = -0^2 + 1 = 1
Right-hand limit:
lim x→0+ {4x - 3} = 4(0) - 3 = -3
Since the left-hand limit and right-hand limit are not equal, the limit of f(x) as x approaches 0 does not exist. So the correct answer is (D).
To learn more about right-hand limit visit:https://brainly.com/question/30886116
#SPJ11
Related Questions
DUE SOON PLEASE HELP :((((
If the pattern below continues, in which column would the number 100 be? The number 500?
A | B | C | D | E |
1 | 2 | 3 | 4 | 5 |
9 | 8 | 7 | 6 | ? |
10| 11| 12| 13 | 14|
18| 17| 16| 15| ? |
Answers
Answer:
100: Column A, 500: Column E
Step-by-step explanation:
Each of the columns increases by 9, but just in different ways.
"A" increases by 8, then by 1. 8+1=9
"B" increases by 6, then by 3. 6+3=9
"C" increases by 4, then by 5. 4+5=9
"D" increases by 2, then by 7. 2+7=9
Since all the other numbers in the rows across go up or down by one, it's safe to assume the missing numbers are 5 and 14, which means that the column "E" stays the same, then increases by 9.
100: Knowing that 11×9 is 99, and the pattern of Column A adds 1 after every addition of 8, the next number in the sequence is 100.
500: The closest that the 9 times table gets to 500 are numbers 495 (55×9) and 504 (56×9). And although column "E" increase by 0 and 9, it starts with 5. And 495+5=500, which answers the second question.
Please help me with this

Answers
Answer:
h,c
Step-by-step explanation:
2 × 4^5 + 10 ( 5 × 2 ) - 10 ÷ 2 =
Answers
Answer:
2143
Step-by-step explanation:
2 × 4^5 + 10 (5 × 2) -10 ÷ 2
= 2 × 4^5 + 10 × 10 (-10) ÷ 2
= 2 × 4^5 + 10 × 10 - 10 ÷ 2
= 2 × 4^5 + 10 × 10 - 5
= 2048 + 100 - 5
= 2148 - 5
= 2143
Answer:
Your answer is 2143
Step-by-step explanation:
2 × 4^5 + 10 × 10 - 10 ÷ 2
*How i got the -5 is becuase 10/2 = 5
= 2 × 4^5 + 10 × 10 - 5
* How i go the 100 is becuase 10 *10 = 100
2048 + 100 - 5
How i go 2148 is becuase 2048+100 = 2148
2148 - 5
Answer = 2143
An automatic machine in a manufacturing process is operating groperly if the iengths of an important subcomponent are normally distributed with a mean of izal cri and a otandard deviation of 5.6 cm. A. Find the probability that one selected subcomponent is longer than 122 cm, Probability = B3. Find the probability that if 3 subcomponents are randomly selected, their mean length exceeds 122 cm. Probability win C. Find the probabilify that if 3 are randomly selected, ail 3 have lengths that exceed 122 cm. Probability =
Answers
A. The probability that one selected subcomponent is longer than 122 cm can be found by calculating the area under the normal distribution curve to the right of 122 cm. We can use the z-score formula to standardize the value and then look up the corresponding probability in the standard normal distribution table.
z = (122 - μ) / σ = (122 - 100) / 5.6 = 3.93 (approx.)
Looking up the corresponding probability for a z-score of 3.93 in the standard normal distribution table, we find that it is approximately 0.9999. Therefore, the probability that one selected subcomponent is longer than 122 cm is approximately 0.9999 or 99.99%.
B. To find the probability that the mean length of three randomly selected subcomponents exceeds 122 cm, we need to consider the distribution of the sample mean. Since the sample size is 3 and the subcomponent lengths are normally distributed, the distribution of the sample mean will also be normal.
The mean of the sample mean will still be the same as the population mean, which is 100 cm. However, the standard deviation of the sample mean (also known as the standard error) will be the population standard deviation divided by the square root of the sample size.
Standard error = σ / √n = 5.6 / √3 ≈ 3.24 cm
Now we can calculate the z-score for a mean length of 122 cm:
z = (122 - μ) / standard error = (122 - 100) / 3.24 ≈ 6.79 (approx.)
Again, looking up the corresponding probability for a z-score of 6.79 in the standard normal distribution table, we find that it is extremely close to 1. Therefore, the probability that the mean length of three randomly selected subcomponents exceeds 122 cm is very close to 1 or 100%.
C. If we want to find the probability that all three randomly selected subcomponents have lengths exceeding 122 cm, we can use the probability from Part A and raise it to the power of the sample size since we need all three subcomponents to satisfy the condition.
Probability = (0.9999)^3 ≈ 0.9997
Therefore, the probability that if three subcomponents are randomly selected, all three of them have lengths that exceed 122 cm is approximately 0.9997 or 99.97%.
Based on the given information about the normal distribution of subcomponent lengths, we calculated the probabilities for different scenarios. We found that the probability of selecting a subcomponent longer than 122 cm is very high at 99.99%. Similarly, the probability of the mean length of three subcomponents exceeding 122 cm is also very high at 100%. Finally, the probability that all three randomly selected subcomponents have lengths exceeding 122 cm is approximately 99.97%. These probabilities provide insights into the performance of the automatic machine in terms of producing longer subcomponents.
To know more about probability follow the link:
https://brainly.com/question/251701
#SPJ11
How can I tell if something is a linear expression or a non-linear expression?
Answers
Answer:
An expression is linear if it forms a straight line when you graph it.
A non-linear expression doesn't form a straight line when you graph it.
Step-by-step explanation:
suppose that we flip a fair coin until either it comes up tails twice or it is flipped it six times. what is the expected number of times we flip the coin? (enter the value of probability in decimals. round the answer to two decimal places.)
Answers
The value of the probability is 3.75.
What is a probability?It is a branch of mathematics. The possibility of the outcome of any random event is termed as probability. The range of the probability must be between o to 1. Here o indicates impossibility of an event and 1 indicates certainty. Probability can be expressed in proportions. Probability deals in finding the occurrence of an event. It is based on the possible chances of something that happen. Probability is of 3 types. They are:
1.Theoretical probability
2.Experimental probability
3.Axiomatic probability
P(N=2)=P(TT)=14
P(N=3)=P(HTT,THT)=28
P(N=4)=P(HHTT;HTHT;THHT)=316
P(N=5)=432
P(N=6)=1−14−28−316−432=316
E(N)=2(14)+3(28)+4(316)+5(432)+6(316)=154=3.75
The value of the probability up to 2 decimal places is 3.75
To know more about probability, visit:
brainly.com/question/11234923
#SPJ4
Help I need to find the area????!!!?!?!?
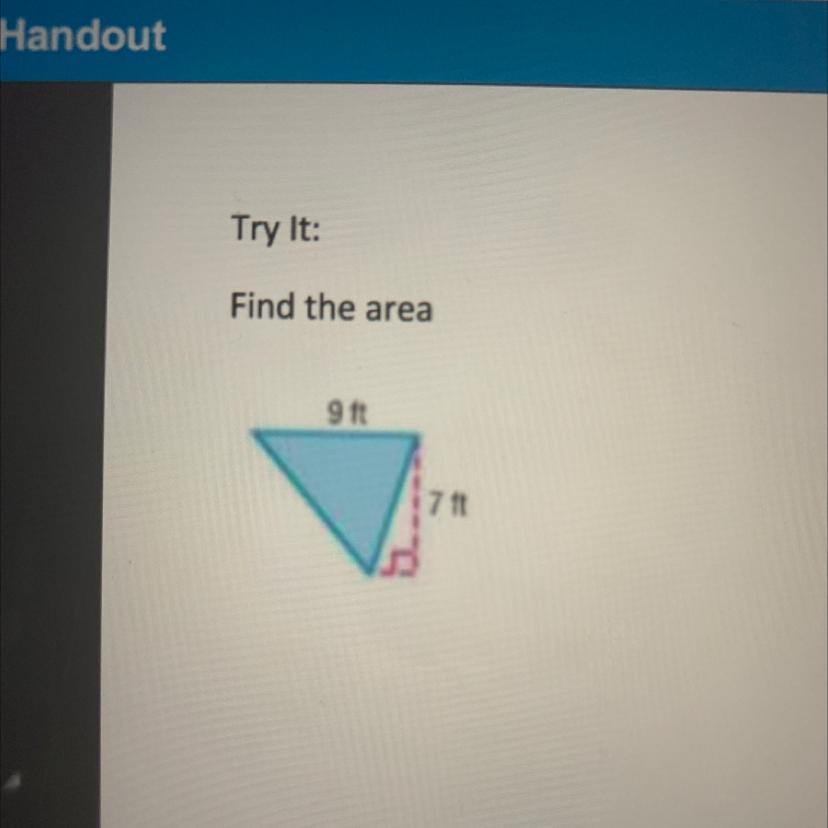
Answers
What is the slope of the line that passes through the points (−8,−1) and (−6,−2)? Write your answer in simplest form.
Answers
Answer:
m = -1/2
Step-by-step explanation:
Recall that slope = (change in y) / (change in x).
Going from (−8,−1) to (−6,−2), x increases by 2 (because -6 - (-8) = 2), and
y decreases by 1. Thus, the slope here is
m = (change in y) / (change in x) = (-1) / 2 = -1 / 2
m = -1/2
The r in the simple interest formula stands for rate which best describes how to use rate in formula

Answers
Convert it to a decimal and multiply is the best way to describe rate in simple interest formula.
Define rate.The real yearly cost of funds over the course of a loan is the annual rate that is charged for borrowing (or made by investing), expressed as a single percentage number. An interest rate indicates how expensive borrowing is or how lucrative saving is. Therefore, if you are a borrower, the interest rate is the sum you pay for borrowing money and is expressed as a percentage of the overall loan amount.
Given
The r in the simple interest formula stands for rate.
Convert it to a decimal and multiply is the best way to describe rate in formula.
To learn more about rate, visit:
https://brainly.com/question/199664
#SPJ1
what are the x-intercepts, y-intercepts, and horizontal and vertical asymptotes? (if an answer does not exist, enter dne. enter your asymptotes as a comma-separated list.) g(x)
Answers
Using the graphs and the curves shown in the graph we can identify many characteristics from it. The intercepts are intersections with the axes and asymptotes are line running to infinity close to axes.
What is a graph?In mathematics, "graph" can refer to (at least) two different things. In elementary mathematics, the term "graph" designates a plot or a function graph. A graph is, in the language of mathematicians, a set of points and the connections between some subset of those points (which may be empty).
What are intercepts and asymptotes?The points on a graph where the graph crosses the two axes are known as the intercepts (x-axis and y-axis). The x-coordinate is the location where the graph crosses the x-axis, and the y-coordinate is the location where the graph crosses the y-axis.
A line that keeps moving in the direction of a particular curve but never actually touches it.
x-intercept = point where the curve of the function crosses x-axis.
y-intercept = point where the curve of the function crosses y-axis.
Horizontal asymptotes = curve which moves towards infinity along the x-axis but doesn't crosses the x-axis.
Vertical asymptotes = curve which moves towards infinity along the y-axis but doesn't crosses the y-axis.
To learn more about graphs visit:
https://brainly.com/question/17267403
#SPJ4
Which diagram shows the X method being used correctly to factor the trinomial 2x² – 3x + 1?

Answers
The diagram that shows the X method being used correctly to factor the trinomial is (c)
How to determine the diagram of the X methodFrom the question, we have the following parameters that can be used in our computation:
2x² – 3x + 1
Next, we expand the expression
This gives
2x² – 2x - x + 1
Factorize the expression
2x(x - 1) -1(x - 1)
Factor out x - 1
(2x - 1)(x - 1)
The structure of the X method diagram is
Product of factors
Coefficient of term 1 Coefficient of term 2
Sum of factors
In 2x² – 2x - x + 1, we have
Coefficient of term 1 = -2 i.e. the -2 in -2xCoefficient of term 2 = -1 i.e. the -1 in -xMultiply the terms
Product = -2 * -1 = 2
Add the terms
Sum = -2 - 1 = -3
So, we have
2
-2 -1
-3
Hence, the diagram is (c)
Read more about trinomial at
https://brainly.com/question/26501010
#SPJ1
Answer: The correct option is c
Step-by-step explanation:
I jus took the test on edge
The coordinates of the vertices of △MER are M(3,2), E(3,−3), and R(9,−3). Find the side lengths to the nearest hundredth and the angle measures to the nearest degree. Answers;
A) ME = 5; ER = 6, MR ≈ 7.81 m∠E = 90°, m∠M ≈ 50°, m∠R ≈ 40°
B) ME = 6; ER = 5, MR ≈ 7.81 m∠E = 90°, m∠M ≈ 51°, m∠R ≈ 39°
C) ME = 6; ER = 5, MR = 11 m∠E = 90°, m∠M ≈ 50°, m∠R ≈ 40°
D) ME = 5; ER = 6, MR ≈ 7.81 m∠E = 90°, m∠M ≈ 40°, m∠R ≈ 50°
Please give a full explanation I would really appreciate it :)
Answers
Using the Pythagorean theorem and the law of sines, the correct lengths to the nearest hundredth and the angle measures to the nearest degree are: A) ME = 5; ER = 6, MR ≈ 7.81 m∠E = 90°, m∠M ≈ 50°, m∠R ≈ 40°
What is the Pythagorean Theorem?The theorem states that the square of the longest side of a right triangle equals the sum of the squares of the lengths of the other two smaller sides of the right triangle.
The points, M(3,2), E(3,−3), and R(9,−3) has been plotted on the graph which shows that angle E is a right triangle, therefore:
m∠E = 90 degrees.
Find ME and ER:
ME = 5 units
ER = 6 units.
Using the Pythagorean theorem, find MR:
MR = √(ME² + ER²)
MR = √(5² + 6²)
MR = √(25 + 36)
MR = 7.81 units
Using the law of sines, find m∠M:
sin M/ER = sin E/MR
sin M/6 = sin 90/7.81
sin M = (sin 90 × 6)/7.81
sin M = 0.7682
M = sin^(-1)(0.7682)
m∠M ≈ 50°
m∠R = 180 - 50 - 90
m∠R = 40°
Thus, the correct lengths to the nearest hundredth and the angle measures to the nearest degree are:
A) ME = 5; ER = 6, MR ≈ 7.81 m∠E = 90°, m∠M ≈ 50°, m∠R ≈ 40°
Learn more about the Pythagorean theorem on:
https://brainly.com/question/343682
#SPJ1

A) √2 is that rational or irrational
Answers
Answer:
Irrational
Step-by-step explanation:
\(\sqrt{2}\) produces 1.41421356237, so it is irrational.
What is the value of -2 to the power of 4
Answers
We can find the value if we write the complete expression:
\((-2)^4=(-2)\cdot(-2)\cdot(-2)\cdot(-2)\)Considering only two factors at a time, and knowing that - * - = +, we have:
\((-2)\cdot(-2)\cdot(-2)\cdot(-2)=4\cdot4=16\)Therefore, (-2)^4 = 16
Answer:
-16!!
-2x-2x-2x-2= -16.
Help me pleaseeeee I need this :( I’ll give your brainliest

Answers
Answer:
ABC & ADE You get these because of the line that separates the two triangles.
A fence was installed around the edge of a rectangular garden. The length, 1, of the fence was 5 feet less than 3 times its width, w. The amount of fencing used was 90 feet. Write a system of equations or write an equation using one variable that models this situation. Determine algebraically the dimensions, in feet, of the garden.
Answers
The dimensions of the garden are 12.5 feet by 30.5 feet.
To model this situation, we can use two equations. Let the width of the rectangular garden be w feet and the length be l feet.
Then:We know that the perimeter of the garden is 90 feet because the amount of fencing used was 90 feet.Perimeter = sum of all sides2(l + w) = 90Divide both sides by 22(l + w)/2 = 45l + w = 45Now,
we also know that the length of the fence, 1, was 5 feet less than 3 times the width,
w.l = 3w - 5Substitute this equation for l in the first equation:3w - 5 + w = 45Simplify:4w - 5 = 45
Add 5 to both sides :4w = 50Divide both sides by 4:w = 12.5
Now that we know the width of the garden is 12.5 feet, we can use the equation for l to find the length:l = 3w - 5l = 3(12.5) - 5l = 30.5
To learn more about : dimensions
https://brainly.com/question/28107004
#SPJ8
find the general solution of the given differential equation. y' + 7x^6y = x^6
Answers
The general solution of the given differential equation is:
y = (1/7) + C * \(exp(-x^7)\)
The exponential of the integral of the coefficient of y, in this case 7x6, provides the integrating factor. The integrating factor is given by the exponential of the integral of the coefficient of y, which in this case is 7x⁶.
The integrating factor is therefore exp(∫ 7x⁶ dx), which can be calculated as exp(x⁷/7).
Multiplying both sides of the differential equation by the integrating factor, we have:
exp(x⁷/7) * y' + 7x⁶ * exp(x⁷/7) * y = x⁶ * exp(x⁷/7)
Using the product rule on the left side, we can rewrite the equation as:
d/dx (exp(x⁷/7) * y) = x⁶ * exp(x⁷/7)
Integrating both sides with respect to x, we get:
exp(x⁷/7) * y = ∫ x⁶ * exp(x⁷/7) dx
The integral on the right side can be solved using integration by parts. Let's denote u = x⁶ and dv = exp(x⁷/7) dx. Then, du = 6x⁵ dx and v = 7/7 * exp(x⁷/7) = exp(x⁷/7).
Using the formula for integration by parts:
∫ u dv = uv - ∫ v du
We have:
∫ x⁶ * exp(x⁷/7) dx = x⁶ * exp(x⁷/7) - ∫ exp(x⁷/7) * 6x⁵ dx
Simplifying the integral on the right side, we obtain:
∫ exp(x⁷/7) * 6x⁵ dx = 6 * ∫ x⁵ * exp(x⁷/7) dx
We can apply integration by parts again to this integral, with u = x⁵ and dv = exp(x⁷/7) dx.
Continuing this process, we will eventually reach an integral of the form ∫ exp(x⁷/7) dx, which can be expressed in terms of special functions called exponential integrals.
Once we have the value of this integral, we can substitute it back into the expression for the integral of x⁶ * exp(x⁷/7) dx.
Finally, we divide both sides of the equation by exp(x⁷/7) and solve for y:
y = (1/exp(x⁷/7)) * (∫ x⁶ * exp(x⁷/7) dx)
The resulting expression will give the general solution to the given differential equation.
To solve this linear first-order ordinary differential equation, we can use an integrating factor. The integral of the coefficient of y's exponential integral, in this case 7x⁶, provides the integrating factor.
The integrating factor is therefore exp(∫ 7x⁶ dx), which can be calculated as exp((7/7) * x⁷) = exp(x⁷).
Multiplying both sides of the differential equation by the integrating factor, we have:
exp(x⁷) * y' + 7x⁶ * exp(x⁷) * y = x⁶ * exp(x⁷)
We can rewrite this equation as follows:
d/dx (exp(x⁷) * y) = x⁶ * exp(x⁷)
Integrating both sides with respect to x, we get:
exp(x⁷) * y = ∫ x⁶ * exp(x⁷) dx
To evaluate this integral, we can make a substitution. Let's substitute u = x⁷, then du = 7x⁶ dx.
The integral becomes:
(1/7) ∫ exp(u) du = (1/7) * exp(u) + C = (1/7) * exp(x⁷) + C
Now, dividing both sides of the equation by exp(x⁷), we have:
y = (1/7) + C * exp(-x⁷)
Therefore, the general solution of the given differential equation is:
y = (1/7) + C * exp(-x⁷)
where C is an arbitrary constant.
To know more about integration follow the given link:
https://brainly.com/question/30094386
#SPJ4
Provide the missing reasons in the proof.
Choices for the above proof:
Angle Addition Postulate
ASA Congruence Postulate
Given
Definition of right triangle
∆ is a right triangle
51° + 39° = ∠;
90° = ∠;
∠ is a right angle
Definition of right angle
Angle Congruence Postulate

Answers
The angle ∠DEF is equal to 90 degrees. Then the triangle ΔDEF will be a right-angle triangle.
What is a right-angle triangle?It's a form of a triangle with one 90-degree angle that follows Pythagoras' theorem and can be solved using the trigonometry function. The Pythagoras theorem states that the sum of two squares equals the squared of the longest side.
The angle ∠DEG = 51° and angle ∠GEF = 39°.
Then prove that the triangle ΔDEF will be a right-angle triangle. Then we have
We know that if one angle of the triangle is 90 degrees then the triangle will be named a right-angle triangle.
The sum of the angle ∠DEG and ∠GEF will be
∠DEF = ∠DEG + ∠GEF
∠DEF = 51° + 39°
∠DEF = 90°
Then the triangle ΔDEF will be a right-angle triangle.
More about the right-angle triangle link is given below.
https://brainly.com/question/3770177
#SPJ1
Factor the difference of two cubes
8v^3-27
i’ll give brainliest
Answers
27 - 8v3.........................
Answer:
\(8v^{3} +27=(2v)^{3} +3^{3}=(2v+3)(4v^{2} -6v+9)\\\)
Step-by-step explanation:
from formula a³ – b³ = (a – b) (a² + ab + b² )
Please help me with the math

Answers
20, 8
0.5, 4.1
hope this helps!!
Apply De Morgan's law repeatedly to each Boolean expression until the complement operations in the expression only operate on a single variable. For example, there should be no xy¯ or x+y¯ in the expression. Then apply the double complement law to any variable where the complement operation is applied twice. That is, replace x¯¯ with x.
a. 1/ x + yz + u b. 1/x(y + 2)u c. 1/(x + y)(uv + x y) d. 1/xy + yz + xz
Answers
The simplified expression using De Morgan's law are a)x'y'z'u b)x'y'u c): x'y'u and d)x'y'z'+xy'z'+xyz.
The main idea is to simplify each Boolean expression by repeatedly applying De Morgan's law until each complement operation operates on a single variable.
Then, apply the double complement law to simplify the expression further. In the end, the simplified expression should contain only AND and OR operations without any complement operators acting on multiple variables.
a. 1/ x + yz + u can be simplified using De Morgan's law to: (x'y'z')u'. Then, applying the double complement law, we get the simplified expression as: x'y'z'u.
b. 1/x(y + 2)u can be simplified using De Morgan's law to: x'(y'+2')u'. Then, applying the double complement law, we get the simplified expression as: x'y'u.
c. 1/(x + y)(uv + xy) can be simplified using De Morgan's law to: (x'y')(u' + x'y'). Then, applying the double complement law, we get the simplified expression as: x'y'u.
d. 1/xy + yz + xz can be simplified using De Morgan's law to: (x'+y')(y'+z')(x'+z'). Then, applying the double complement law, we get the simplified expression as: x'y'z'+xy'z'+xyz.
In summary, to simplify Boolean expressions, we can apply De Morgan's law repeatedly and then use the double complement law to remove complement operators acting on a single variable twice.
For more questions like De Morgan's law click the link below:
https://brainly.com/question/29073742
#SPJ11
a rectangle has a perimeter of 128 inches. the length is four less than twice the width. what is the length of the rectangle?
Answers
The length of the rectangle is approximately 41.34 inches.
Let's assume the width of the rectangle is represented by the variable w. According to the given information, the length of the rectangle is four less than twice the width, which can be expressed as 2w - 4.
The perimeter of a rectangle is calculated by adding the lengths of all four sides. In this case, the perimeter is given as 128 inches. Since a rectangle has two pairs of equal sides, we can set up the equation:
2w + 2(2w - 4) = 128.
Simplifying the equation, we get:
2w + 4w - 8 = 128,
6w - 8 = 128,
6w = 136,
w = 22.67.
So, the width of the rectangle is approximately 22.67 inches. To find the length, we can substitute this value back into the expression 2w - 4:
2(22.67) - 4 = 41.34.
Therefore, the length of the rectangle is approximately 41.34 inches.
In summary, the length of the rectangle is approximately 41.34 inches. This is determined by setting up a system of equations based on the given information: the perimeter of the rectangle being 128 inches and the length being four less than twice the width.
By solving the system of equations, we find that the width is approximately 22.67 inches, and substituting this value back, we obtain the length of approximately 41.34 inches.
To know more about length refer here:
https://brainly.com/question/2497593
#SPJ11
Give in the speeds of each Runner determine who runs the fastest Emily runs 15 ft per second no one runs 358 ft and 36 seconds Liz runs 1 mi in 405 seconds Zack runs 768 feet in 1 minute
Answers
Emily runs at the fastest speed of 15 ft per second, Liz runs at 13.03 ft per second, and Zack runs at 12.8 ft per second.
What is speed?Speed is defined as the ratio of the time distance travelled by the body to the time taken by the body to cover the distance. Speed is the ratio of the distance travelled by time. The unit of speed in miles per hour.
Given that Emily runs 15 ft per second no one runs 358 ft and 36 seconds Liz runs 1 mi in 405 seconds Zack runs 768 feet in 1 minute.
Emily's speed = 15 ft/sec
Liz's speed = 1 mile per 405 sec = 5280/405 = 13.03 ft /sec
Zack's speed = 768 / 60 = 12.8 ft /sec
Therefore, Emily runs at the fastest speed of 15 ft per second, Liz runs at 13.03 ft per second, and Zack runs at 12.8 ft per second.
To know more about Speed follow
brainly.com/question/6504879
#SPJ2
At the beginning of the year, Alyssa had $100 in savings and saved an additional $7
each week thereafter. Colton started the year with $55 and saved $10 every week. Let
A represent the amount of money Alyssa has saved t weeks after the beginning of the year and let C represent the amount of money Colton has saved t weeks after the
beginning of the year. Write an equation for each situation, in terms of t, and determine the amount of money Alyssa and Colton have saved in the week that they
have the same amount of money saved.
Answers
Answer:the answer is 4.55
Step-by-step explanation:
using chebyshev's theorem, solve these problems for a distribution with a mean of 57 and a standard deviation of 25 . round to at least 2 decimal places and final answers to at least one decimal place if needed.
Answers
The proportion of the data that lies within 2 standard deviations of the mean for a distribution with a mean of 57 and a standard deviation of 25 is at least 0.75.
Formally known as Chebyshev's inequality, this theorem states that for any distribution, the proportion of the data that lies within k standard deviations of the mean is at least 1 - (1/k²). For this problem, k = 2 since the question is asking to find the proportion of the data that is within 2 standard deviations of the mean.
Thus, the portion of the data that lies within 2 standard deviations of the mean is at least 1 - (1/2²) = 1 - (1/4) = 0.75.
Therefore, the proportion of the data that lies within 2 standard deviations of the mean for a distribution with a mean of 57 and a standard deviation of 25 is at least 0.75.
Learn more about the standard deviation visit:
brainly.com/question/13905583.
#SPJ4
let x be normally distributed with mean μ = 2,500 and standard deviation σ = 800
a. Find x such that P(X ≤ x) = 0.9382. (Round "z" value to 2 decimal places, and final answer to the nearest whole number.)x
b. Find x such that P(X > x) = 0.025. (Round "z" value to 2 decimal places, and final answer to the nearest whole number.) x
c. Find x such that P(2500 ≤ X ≤ x) = 0.1217. (Round "z" value to 2 decimal places, and final answer to the nearest whole number.)
d. Find x such that P(X ≤ x) = 0.4840. (Round "z" value to 2 decimal places, and final answer to the nearest whole number.) x
Answers
Rounding to the nearest whole number, we get x = 2524.
a. Using the standard normal distribution table, we can find the corresponding z-score for the given probability:
P(X ≤ x) = P((X-μ)/σ ≤ (x-μ)/σ) = P(Z ≤ (x-μ)/σ) = 0.9382
From the standard normal distribution table, the closest probability to 0.9382 is 0.9382, which corresponds to a z-score of 1.56. Therefore:
(x - μ) / σ = 1.56
Substituting in the given values for μ and σ, we get:
(x - 2500) / 800 = 1.56
Solving for x, we get:
x = 2500 + 1.56 * 800 = 2728
Rounding to the nearest whole number, we get x = 2728.
b. Again, using the standard normal distribution table, we can find the corresponding z-score for the given probability:
P(X > x) = P((X-μ)/σ > (x-μ)/σ) = P(Z > (x-μ)/σ) = 0.025
From the standard normal distribution table, the closest probability to 0.025 is 0.0249979, which corresponds to a z-score of -1.96. Therefore:
(x - μ) / σ = -1.96
Substituting in the given values for μ and σ, we get:
(x - 2500) / 800 = -1.96
Solving for x, we get:
x = 2500 - 1.96 * 800 = 1144
Rounding to the nearest whole number, we get x = 1144.
c. We can use the same approach as in part (a), but this time we need to find the z-score for the probability between two values:
P(2500 ≤ X ≤ x) = P((X-μ)/σ ≤ (x-μ)/σ) - P((X-μ)/σ ≤ (2500-μ)/σ) = P(Z ≤ (x-μ)/σ) - P(Z ≤ -0.63) = 0.1217
From the standard normal distribution table, the closest probability to 0.1217 is 0.1217, which corresponds to a z-score of 1.17. Therefore:
(x - μ) / σ = 1.17
Substituting in the given values for μ and σ, we get:
(x - 2500) / 800 = 1.17
Solving for x, we get:
x = 2500 + 1.17 * 800 = 3056
Rounding to the nearest whole number, we get x = 3056.
d. We can use the same approach as in part (a):
P(X ≤ x) = P((X-μ)/σ ≤ (x-μ)/σ) = P(Z ≤ (x-μ)/σ) = 0.4840
From the standard normal distribution table, the closest probability to 0.4840 is 0.4838, which corresponds to a z-score of 0.03. Therefore:
(x - μ) / σ = 0.03
Substituting in the given values for μ and σ, we get:
(x - 2500) / 800 = 0.03
Solving for x, we get:
x = 2500 + 0.03 * 800 = 2524
Rounding to the nearest whole number, we get x = 2524.
To learn more about whole number visit: https://brainly.com/question/29766862
#SPJ11
A bag contains 8 apples and 6 oranges. You randomly draw a piece of fruit from the bag, eat it, and then randomly draw another. What is the probability you draw and eat an apple then draw an orange
Answers
Answer:
probability of choosing apple first = 8/14
probability of choosing orange second = 6/13
probability of choosing apple and orange = 8/14 x 6/13 = 24/91
Step-by-step explanation:
△TRG is a right triangle. RG = 17; GT= 22 which is closest to the length of RT?
Answers
The length of RT that is closest to the given information is 27.
In a right triangle, the side opposite the right angle is called the hypotenuse. Let's assume that RT is the hypotenuse of the triangle △TRG.
According to the Pythagorean theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides. In this case, we have:
RT² = RG² + GT²
Substituting the given values, we have:
RT² = 17² + 22²
= 289 + 484
= 773
To find the length of RT, we need to take the square root of both sides:
RT = √773
Calculating this, we find that RT is approximately 27.
Therefore, the length of RT that is closest to the given information is 27.
Visit here to learn more about Pythagorean theorem:
brainly.com/question/14930619
#SPJ11
Find the total surface area of this prism where the cross section is an isosceles triangle 5cm, 13cm, 24cm, 10cm
Answers
Answer: 620 cm2
Step-by-step explanation:
The base of the prism is a rectangle with 24 cm x 10 cm, so the base area is: B = 24 * 10 = 240 cm2
The cross section is a triangle with base = 24 cm and height = 5 cm, so its area is: C = 24 * 5 / 2 = 60 cm2
The sides are rectangles with 10 cm x 13 cm, so their area is: D = 10 * 13 = 130 cm2
The total surface area is: S = B + 2C + 2D = 240 + 2*60 + 2*130 = 620 cm2
there are 16 marbles in a bag 12 of them are blue and 4 are yellow. what is the probability of picking a blue marble then a yellow marble without replacing the first one
11/20
3/7
1/5
Answers
Answer:
1/5
Step-by-step explanation:
the prob that you will pick a blue marble would be 12/16, easy.
then the prob of picking a yellow marble after that would be 4/15 since one marble is already missing. multiply the numerator and denominator of each fraction. so 12 x 4 and 16 x 15 to get 48/240. then divide each by 48 to get 1/5.
the answer is 1/5
hope that solve your problem for whoever gets this question