Answers
Answer:
Option C.
Step-by-step explanation:
\(\sf\:x^{2}-3x+7=0 \)
Use the biquadratic formula.
\(\sf\:\x=\frac{-\left(-3\right)(+/-)\sqrt{\left(-3\right)^{2}-4\times 7}}{2} \)
\(\sf\:x=\frac{-\left(-3\right)(+/-)\sqrt{9-4\times 7}}{2} \)
\(\sf\:x=\frac{-\left(-3\right)(+/-)\sqrt{9-28}}{2} \)
\(\sf\:x=\frac{-\left(-3\right)(+/-)\sqrt{-19}}{2} \)
\(\sf\:x=\frac{3(+/-)\sqrt{19}}{2} \)
Positive sign:
\(\boxed{\sf\:x=\frac{3+\sqrt{19}}{2}} \)
Negative sign:
\(\boxed{\sf\:x=\frac{3-\sqrt{19}}{2}} \)
Hope it helps ⚜
Related Questions
If the sum of an infinite geometric series is \( \frac{15625}{24} \) and the common ratio is \( \frac{1}{25} \), determine the first term. Select one: a. 625 b. 3125 c. 25 d. 125
Answers
The first term of the infinite geometric series is 625.Let's dive deeper into the explanation.
We are given that the sum of the infinite geometric series is \(\( \frac{15625}{24} \)\)and the common ratio is\(\( \frac{1}{25} \).\)The formula for the sum of an infinite geometric series is \(\( S = \frac{a}{1 - r} \)\), where \( a \) is the first term and \( r \) is the common ratio.
Substituting the given values into the formula, we have \(\( \frac{15625}{24} = \frac{a}{1 - \frac{1}{25}} \).\)To find the value of \( a \), we need to isolate it on one side of the equation.
To do this, we can simplify the denominator on the right-hand side.\(\( 1 - \frac{1}{25} = \frac{25}{25} - \frac{1}{25} = \frac{24}{25} \).\)
Now, we have \(\( \frac{15625}{24} = \frac{a}{\frac{24}{25}} \).\) To divide by a fraction, we multiply by its reciprocal. So, we can rewrite the equation as \( \frac{15625}{24} \times\(\frac{25}{24} = a \).\)
Simplifying the right-hand side of the equation, we get \(\( \frac{625}{1} = a \).\)Therefore, the first term of the infinite geometric series is 625.
In conclusion, the first term of the given infinite geometric series is 625, which corresponds to option (a).
learn more about geometric series here here
https://brainly.com/question/30264021
#SPJ11
For a project in his Geometry class, Tyler uses a mirror on the ground to measure the height of his school building. He walks a distance of 14.65 meters from his school, then places a mirror on flat on the ground, marked with an X at the center. He then steps 0.8 meters to the other side of the mirror, until he can see the top of the school clearly marked in the X. His partner measures the distance from his eyes to the ground to be 1.15 meters. How tall is the school? Round your answer to the nearest hundredth of a meter.

Answers
Answer:
The height of the school building is approximately 21.06 meters
Step-by-step explanation:
The method of Geometry Tyler is using to determine the height of his school building is through the property that similar triangles have a common ratio of corresponding their sides
The given parameters for the triangle formed by Tyler and the mirror are;
The distance from Tyler's eyes to the ground = 1.15 meters
The horizontal distance between Tyler and the mirror at X = 0.8 m
The parameters of the triangle formed by the height, h, of the school building and the mirror at X are;
The horizontal distance between the school building and the mirror = 14.65 m
The height of the school building = h
Therefore, we have;
\(\dfrac{The \ distance \ from \ Tyler's \ eyes \ to \ the \ ground}{The \ height \ of the \ school \ building} =\dfrac{Tyler's \ horizontal \ distance \ from \ mirror }{The \ building \ to \ mirror \ horizontal \ distance }\)Therefore;
\(\dfrac{1.15 \, m}{h} = \dfrac{0.8 \ m}{14.65 \ m}\)
\(h = \dfrac{1.15 \, m \times 14.65 \, m }{0.8 \, m} = 21.059375 \ m\)
The height of the school building h to the nearest hundredth meter ≈ 21.06 m.
Here is a rectangle with length 5 units and width 2 units.
1. What is the area of the rectangle?
2. Dilate rectangle ABCD from point A by a scale factor of 2. Calculate the area of the image.
3. Dilate rectangle ABCD from point A by a scale factor of 3. Calculate the area of the image.

Answers
This refers to the ratio between the scale of a given original object and a new object. It is its representation but of a different size (bigger or smaller). For example, if we have a rectangle of sides 2 cm and 4 cm, we can enlarge it by multiplying each side by a number, say 2.
Solving for the area and scale factor we have:
L= 5 units
W = 2 units
The area of the rectangle =L * WA = (5 x 2)
A = 10 square units.
If the rectangle is dilated from point A by a scale factor of 2, the area of the image:A= (Scale factor of L * W)* L * W
= (2 x 2 x 5 x 2)
A = 40 square units.
If the rectangle is dilated from point A by a scale factor of 3, the area of the image is:A= (Scale factor of L * W)* L * W
= (3 x 3 x 5 x 2)
A= 90 square units
Learn more about area on
https://brainly.com/question/29082330
#SPJ1
The sum of 9 and y is less than or equal to 16.
Answers
Answer:
\(9+y\) ≤ \(16\)
Step-by-step explanation:
The sum of \(9\) and \(y\) which is \(9+y\) is less than or equal to 16, which is ≤ \(16\)
Hope this is helpful.
Solve for x in the equation x squared + 10 x + 12 = 36. x = –12 or x = 2 x = –11 or x = 1 x = –2 or x = 12 x = –1 or x = 11
Answers
Answer
x = 2 and x = -12
Step-by-step explanation:
Answer:
^^^^its a
theyre right
Step-by-step explanation:
50 POINTS IF ANSWERED PLS!!!!
Which angle is the biggest based on the sides of the triangles below? Explain your reasoning.

Answers
Answer:
angle c
Step-by-step explanation:
since the largest angle will be across from the longest side, angle c is the right answer because it is across from the longest side which measures 35 cm.
hope this helps
implement f using a single 4-to-1 multiplexer and two inverters. (5 points)
Answers
The function f can be implemented using a single 4-to-1 multiplexer and two inverters.
A 4-to-1 multiplexer is a digital logic component that selects one of four input signals based on the select lines. It has four data inputs (D0, D1, D2, D3), two select lines (S0, S1), and one output (Y). By properly connecting the inputs and select lines, we can realize the desired function f.
To implement the function f using a single 4-to-1 multiplexer and two inverters, we need to carefully assign the input signals and select lines to achieve the desired behavior. The truth table of the function f will guide us in determining the appropriate connections.
First, we can use the inverters to complement the required inputs if needed. Then, we can connect the complemented and uncomplemented inputs to the select lines of the multiplexer. The output of the multiplexer will be the result of the function f.
By carefully selecting the input assignments and connections, we can effectively implement the function f using a single 4-to-1 multiplexer and two inverters. This approach offers a compact and efficient solution for realizing the desired logic function.
Learn more about lines here: https://brainly.com/question/31454782
#SPJ11
I need the set up and I'm solving for x, please help.

Answers
Answer:
100 + 40 + 2x = 180
combine like terms
140 +2x = 180
-140 -140
2x = 40
/2 /2
x = 20
5x-7-2x=10 what is x equaled to
HELP ASAP!!!!
Answers
Answer:
x=-1
Step-by-step explanation:
5x-2x-7=-10
3x-7=-10
3x-7+7=-10+7
3x=-3
x=-1
\(\text{Hey \: there!}\)
\(\text{5x - 7 - 2x = 10}\)
First you'll have to COMBINE all of your like terms\(\bf{(5x - 2x) \: which \: gives \: us \: 3x}\)
New equation becomes: \(\bf{3x - 7 = 10}\)Add by 7 on your sides\(\text{3x - 7 + 7 = 10 + 7}\)
Cancel out\(\bf{ - 7 + 7 \: because \: it \: gives \: you \: 0}\)
\(\bf{10 + 7 = 17}\)
New equation: \(\bf{3x = 17}\)Divide by 3 on both sides\( \frac{3x}{3} = \frac{17}{3} \)
Cancel out \( \frac{3x}{3} \: \bf{because \: it \: gives \: you \: 1 \: and \: not \: x \: }\)\(\text{we \: cant \: divide \: 17 \: from \: 3 \: because \: itll \: give \: us \: a \: decimal}\)
\(\boxed{\bf{thus \: your \: answer \: is \: \bf{ \frac{17}{3} }}}\)
Good luck on your assignment and enjoy your day!~
\(\frak{loveyourselffirst:)}\)
Determine the Cartesian equation of the plane which contains the point A (3,-1,1) and the straight line defined by the equations
x+1/2=y-1/-3=z-2/3
Answers
To determine the Cartesian equation of the plane that contains the point A (3, -1, 1) and the straight line defined by the equations:
x + 1/2 = (y - 1)/(-3) = (z - 2)/3
First, we need to find the direction vector of the line. From the given equations, we can see that the coefficients of x, y, and z in the line equation represent the direction ratios. Therefore, the direction vector of the line is given by:
v = <1, -1/3, 1/3>
Now, let's find the normal vector of the plane. Since the plane contains the line, the normal vector of the plane should be perpendicular to the direction vector of the line. Thus, the normal vector of the plane is parallel to the vector <1, -1/3, 1/3>.
Next, we can use the point A (3, -1, 1) and the normal vector of the plane to write the equation of the plane in Cartesian form using the formula: Ax + By + Cz = D
where (A, B, C) is the normal vector of the plane, and D is the constant term.
Substituting the values, we have: 1 * (x - 3) - (1/3) * (y + 1) + (1/3) * (z - 1) = 0
Multiplying through by 3 to eliminate fractions, we get: 3(x - 3) - (y + 1) + (z - 1) = 0
Simplifying further:
3x - 9 - y - 1 + z - 1 = 0
3x - y + z - 11 = 0
Therefore, the Cartesian equation of the plane that contains the point A (3, -1, 1) and the given line is 3x - y + z - 11 = 0.
To know more about Cartesian equation visit:
https://brainly.com/question/32622552
#SPJ11
Find a general solution to the differential equation. y ′′
−6y ′
+9y=t −5
e 3t
The general solution is y(t)=c 1
e 3t
+c 2
te 3t
+ 12
1
t −3
e 3t
Answers
The general solution to the given differential equation is
\(y(t) = c1 e^(3t) + c2 t e^(3t) - (1/2)t - (1/6)e^(3t) + 12\)
Finding general solution to differential equationFind the associated homogeneous equation by setting the right-hand side to zero:
y'' - 6y' + 9y = 0
The characteristic equation is
\(r^2 - 6r + 9 = 0,\)
r = 3.
Therefore, the general solution to the homogeneous equation is:
\(y_h(t) = (c1 + c2t) e^(3t)\)
\(y_p(t) = At + Be^(3t)\)
where A and B are constants to be determined. We take the first and second derivatives of y_p(t):
\(y_p'(t) = A + 3Be^(3t) \\
y_p''(t) = 9Be^(3t)\)
Substitute these expressions into the differential equation
\(9Be^(3t) - 6(A + 3Be^(3t)) + 9(At + Be^(3t)) \\ = t - 5e^(3t)\)
By simplifying
\((9A - 6B)t + (9B - 6A + 9B)e^(3t) = t - 5e^(3t)\)
Equating the coefficients of t and e^(3t), we get the following system of equations:
9A - 6B = 1
-6A + 18B = -5
Solving for A and B, we get A = -3/2 and B = -1/6. Therefore, the particular solution is:
\(y_p(t) = (-3/2)t - (1/6)e^(3t)\)
The general solution to the non-homogeneous equation is the sum of the homogeneous and particular solutions:
\(y(t) = y_h(t) + y_p(t) = (c1 + c2t) e^(3t) - (3/2)t - (1/6)e^(3t)\)
Simplifying, we get:
\(y(t) = c1 e^(3t) + c2 t e^(3t) - (1/2)t - (1/6)e^(3t) + 12\)
Hence, the general solution to the differential equation is
\(y(t) = c1 e^(3t) + c2 t e^(3t) - (1/2)t - (1/6)e^(3t) + 12\)
where c1 and c2 are arbitrary constants.
Learn more on differential equation on https://brainly.com/question/28099315
#SPJ4
The general solution is y(t) = y_h(t) + y_p(t)y(t)
= (c₁ + c₂t)e^(3t) + (t/9)e^(3t) - 1 + 12/t^3 e^(3t)
Given differential equation is y'' - 6y' + 9y = te^(3t) - 5.
The characteristic equation of the differential equation is obtained by putting
t = 0.y'' - 6y' + 9y
= 0
Using auxiliary equation, we getr² - 6r + 9 = 0On factorizing, we get(r - 3)² = 0 r = 3 (repeated roots)So, the homogeneous solution is
y_h(t) = (c₁ + c₂t)e^(3t)
For particular solution, let's assume
y_p(t) = Ate^(3t) + B
Substitute it in the differential equation.
y'' - 6y' + 9y = te^(3t) - 5
Differentiate the assumed solution
\(y'_p(t) = Ae^(3t) + 3Ate^(3t) + B3Ate^(3t) + 3Ae^(3t) = 3Ate^(3t) + 3Ae^(3t) = 3A(e^(3t))(t + 1)Similarly, y''_p(t) = 9Ae^(3t) + 6Ate^(3t) + 3Ae^(3t) = 3A(e^(3t))(2t + 1)\)
Substitute all these in the given differential equation.
\(3A(e^(3t))(2t + 1) - 6[3A(e^(3t))(t + 1) + B] + 9[Ate^(3t) + B] = te^(3t) - 5\)
Group the like terms.
6A(e^(3t))t - 6B + 9B = te^(3t) - 5 + 3A(e^(3t))2t
Simplify the equation.
3A(e^(3t))2t + 6A(e^(3t))t + 3B = te^(3t) - 5
Equating the coefficients of like terms,A = 1/9 and B = -1So, the particular solution is
y_p(t) = (t/9)e^(3t) - 1
learn more about general from
https://brainly.com/question/23819325
#SPJ11
-3x-y=9
y=-3x+9
(select the correct answer for the solution to the following system of equations)
A: (1,6)
B: (0,-9)
C: infinite solutions
D: no solution
Answers
Answer:
D: no solution
...because none of the answers work for both of the equations when you plug in the x and y values
A 300-liter tank initially contains 175 liters Of Fuel. A pump empties the tank at a rate of 7.5 Liters per minute. which of these represents a function that models the number of liters of fuel in the tank after X minutes

Answers
Answer:
Option (D)
Step-by-step explanation:
Rate of emptying the fuel tank = 7.5 liters per minute
Fuel emptied in x minute = 7.5x liters
Volume of the fuel in the fuel tank initially = 175 liters
Therefore, amount of fuel left in the tank after x minutes = (175 - 7.5x) liters
Function representing the emptying of the fuel tank will be,
f(x) = 175 - 7.5x
Option (D) will be the answer.
plz solve this question urgent

Answers
9514 1404 393
Answer:
2/15
Step-by-step explanation:
The given expression for θ can be rewritten to ...
5sin(θ + arctan(-3/4)) = 0
This will have solutions ...
θ +arctan(-3/4) = nπ
θ = nπ - arctan(-3/4) = nπ + arctan(3/4)
__
The corresponding values of sine and cosine will be ...
sin(arctan(3/4)) = 3/5
cos(arctan(3/4) = 4/5
or both values may be negative. Either sign will give the same result in the expression we're to find.
(2sin(θ) -cos(θ))/(sin(θ) +3cos(θ)) = (2(3/5) -(4/5))/(3/5 +3(4/5))
= ((6 -4)/5)/((3+12)/5) = 2/15
\(\boxed{\dfrac{2\sin\theta-\cos\theta}{\sin\theta+3\cos\theta}=\dfrac{2}{15}}\)
The sum of two numbers is 72. The greater number is 8 more than the smaller number. Which equation can be used to
solve for the smaller number?
O x-(X + 8) = 72
O x + (x + 8) = 72
O X(X + 8) = 72
O x(x - 8) = 72
Answers
to avoid a possible collision with a manned airplane, you estimate that your small ua climbed to an altitude greater than 600 feet agl. to whom must you report the deviation?
Answers
If you operate a small unmanned aircraft (UA) and deviate from your approved flight plan greater than 600 feet agl to avoid a possible collision with a manned airplane, you may need to report the deviation to;
the Federal Aviation Administration (FAA).
The FAA requires all small UAs to comply with certain regulations and guidelines, including the requirement to maintain an altitude of no more than 400 feet above ground level (AGL) unless otherwise authorized.
If you deviate from your approved flight plan, such as by climbing to an altitude greater than 600 feet AGL to avoid a possible collision with a manned airplane, you may need to report the deviation to the FAA.
It is important to follow all FAA regulations and guidelines for small UAs to ensure the safety of other aircraft and people on the ground. If you are unsure about how to report a deviation or what regulations apply to your specific UA, you can contact the FAA for guidance.
Learn more about Federal Aviation Administration (FAA) at: brainly.com/question/30319685
#SPJ4
Suppose we want to choose 5 letters, without replacement, from 16 distinct letters.

Answers
Answer:
a)you can do this two ways
b)you have only one way you can do it
what is 5 3/4 subtracted by 5/8
Answers
Answer:
\(5\frac{1}{8}\)
Step-by-step explanation:
5 3/4 = 23/4
(23/4)2 = 46/8
46/8 - 5/8 = 41/8 = 5 1/8
Endpoint: (7,1), Midpoint: (-8,-9)
Answers
Answer:
Step-by-step explanation:
(x+7)/2= -8
x + 7 = -16
x = -9
(y + 1)/2 = -9
y + 1 = -18
y = -19
(-9, -19)
Hey there, I need help! Which line is perpendicular to the line shown in the graph?
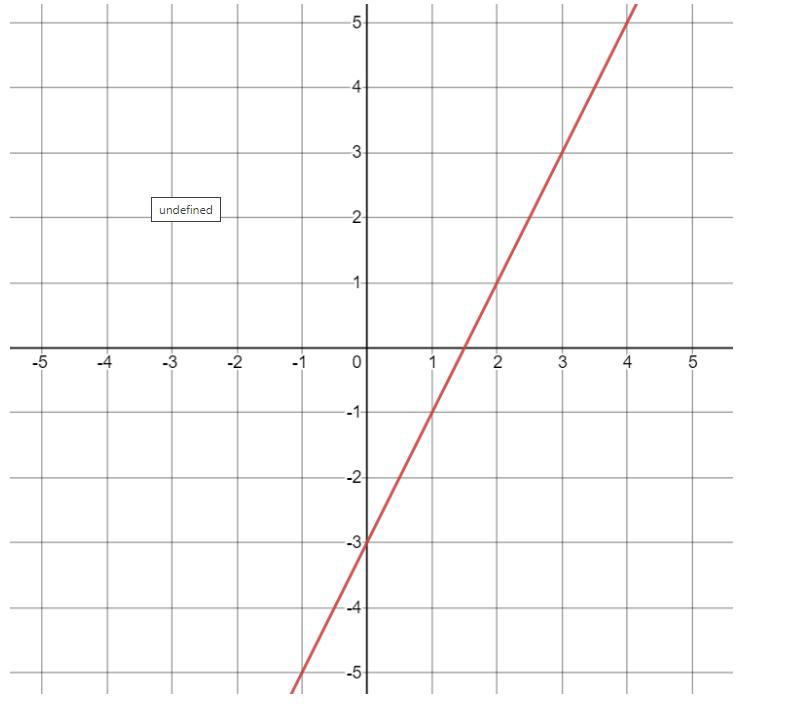

Answers
Answer:
y = - \(\frac{1}{2}\) x + 1
Step-by-step explanation:
calculate the slope m of the given line using the slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (0, - 3) and (x₂, y₂ ) = (2, 1) ← 2 points on the line
m = \(\frac{1-(-3)}{2-0}\) = \(\frac{1+3}{2}\) = \(\frac{4}{2}\) = 2
given a line with slope m then the slope of a line perpendicular to it is
\(m_{perpendicular}\) = - \(\frac{1}{m}\) = - \(\frac{1}{2}\)
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
the only line with m = - \(\frac{1}{2}\) , is
y = - \(\frac{1}{2}\) x + 1 ← perpendicular line
Which equation has the same solution as
x2+4x-13=-7
Answers
Answer:
6x - 3 + 4x = 13
10x - 3 = 13
10x = 16
x = 1.6
Any equation whose solution is x=1.6 has the same solution as this one has.
Step-by-step explanation:
Test the exactness of ODE, if not, use an integrating factor to make exact and then find general solution: (2xy-2y^2 e^3x)dx + (x^2 - 2 ye^2x)dy = 0.
Answers
It is requred to test the exactness of the given ODE and then find its general solution. Then, if the given ODE is not exact, an integrating factor must be used to make it exact.
This given ODE is:(2xy - 2y²e^(3x))dx + (x² - 2ye^(2x))dy = 0.To verify the exactness of the given ODE, we determine whether or not ∂Q/∂x = ∂P/∂y, where P and Q are the coefficients of dx and dy respectively, as follows: P = 2xy - 2y²e^(3x) and Q = x² - 2ye^(2x).Then, we have ∂P/∂y = 2x - 4ye^(3x) and ∂Q/∂x = 2x - 4ye^(2x).Thus, since ∂Q/∂x = ∂P/∂y, the given ODE is exact.To solve the given ODE, we have to find a function F(x,y) that satisfies the equation Mdx + Ndy = 0, where M and N are the coefficients of dx and dy respectively. This is accomplished by integrating both P and Q with respect to their respective variables. We have:∫Pdx = ∫(2xy - 2y²e^(3x))dx = x²y - y²e^(3x) + g(y), where g(y) is a function of y. We differentiate both sides of this equation with respect to y, set it equal to Q, and then solve for g(y). We have:(d/dy)(x²y - y²e^(3x) + g(y)) = x² - 2ye^(2x)Thus, g'(y) = 0 and g(y) = C, where C is a constant.Substituting the value of g(y) in the equation above, we get:x²y - y²e^(3x) + C = 0, as the general solution.The given ODE is exact, so we can solve it by finding a function that satisfies the equation Mdx + Ndy = 0. After integrating both P and Q with respect to their respective variables, we find that the general solution of the given ODE is x²y - y²e^(3x) + C = 0.
To know more about integrating factor visit:
brainly.com/question/32554742
#SPJ11
what is 655 divided by 27
Answers
Answer:
24.26
Step-by-step explanation:
it is messy
Answer:
24.2592593
Step-by-step explanation:
If a class has a total of 3400 points I can earn how many points would I need to get in total to get at least a 90?
Answers
Answer:
are you asking how many points are needed to get 90% in
a class that has a total of 3400 points ?
id so that is : 3060
Step-by-step explanation:
The odds against an event are 5 to 13. Find the probability that the event will occur.
Answers
It is given that the odd against an event are 5 to 13.
The probability that the event will occur is
\(P=\frac{13}{13+5}=\frac{13}{18}\)Suppose a parole board has to decide whether a prisoner, a convicted murderer, is to be released. The null hypothesis would state that the prisoner has not been rehabilitated. Which one of the following decisions and outcomes represents a Type I error? The prisoner is released and kills a family of five in cold blood within 48 hours. The prisoner is released and becomes a model citizen, The prisoner is denied release when in fact he has been totally rehabilitated The prisoner is denied release and continues to get into trouble within the prison and to spend time in solitary confinement
Answers
The decision and outcome that represents a Type I error in this scenario is if the prisoner is released and kills a family of five in cold blood within 48 hours. A Type I error occurs when the null hypothesis is rejected even though it is actually true. In this case, if the parole board releases the prisoner based on the hypothesis that they have been rehabilitated but in reality, they have not been rehabilitated, it would result in a Type I error. The prisoner's release would lead to a tragic outcome, which could have been avoided if the null hypothesis had not been rejected.
Learn more about Type I error here:
https://brainly.com/question/24320889
#SPJ11
What is the sum of 1/5 and 0.375 as a fraction please help

Answers
So... 0.5+0.375=0.875
0.875 into a fraction is 7/8
To check the answer you simply just type 7divided by 8
In a recent survey, 2\3 of the students
said they rode the bus to school.
There were 24 students who took
the survey. How many said that they
rode the bus to school?
Answers
Answer:
16
Step-by-step explanation:
2/3 of 24 students
2/3 * 24 = 16
what is the area of a triangle that is 24 feet by 36 feet? a) 756 square feet b) 864 square feet c) 1,512 square feet d) 432 square feet
Answers
The area of a triangle is 432 square feet.
What is an area of a triangle?
The total area that is bounded by a triangle's three sides is referred to as the triangle's area. The area of the triangle is the region enclosed by its perimeter or the three sides of the triangle. In essence, it is equal to 1/2 of the height times the base, or A = 1/2 b h.
Here, we have
Given: the area of a triangle that is 24 feet by 36 feet.
base = 24feet
height = 36 feet
We know the area of triangle = (h×b)/2
A = (24 × 36)/2
A = 432 square feet
Hence, the area of a triangle is 432 square feet.
To learn more about the area of a triangle from the given link
https://brainly.com/question/3134284
#SPJ1
For a group of high school students, the correlation between math sat score and total sat score is about r = 0.9935. what can be said about r2? note: r2 = 0.987.
Answers
Math SAT scores explain about 98.7% of the variation in the total SAT scores.
What is a correlation?In statistics, correlation or dependence exists as any statistical relationship, whether causal or not, between two random variables or bivariate data.
A correlation exists as a statistical measure (expressed as a number) that defines the size and direction of a relationship between two or more variables. A correlation between variables, however, does not automatically mean that the change in one variable exists as the cause of the change in the values of the other variable.
Since r² exists = (0.9935)² = 0.9870, we interpret r² as 98.7% of the variation in the y variable exists explained by the x variable.
In context, math SAT score explains about 98.7% of the variation in total SAT score.
To learn more about correlation refer to:
https://brainly.com/question/4219149
#SPJ4
