cos² y– sin²y=1–2sin² y
simplify pls, urgent
Answers
Answer:
Step-by-step explanation:
Cos²y + Sin² y = 1
Therefore, Cos² y = 1 - Sin² y
LHS = Cos² y - Sin² y
= 1 - Sin² y - Sin² y {Combine like terms}
= 1 - 2sin² y = RHS
cos²y - sin²y = 1 - 2sin²y
or, cos²y - sin²y + 2sin²y = 1
or, cos²y + sin²y = 1 [It's a formula]
(Is that what you mean by simplify?)
Related Questions
Is an isosceles triangle always right?
Answers
No, an isosceles triangle is not always a right triangle.
Is an isosceles triangle always right?An isosceles triangle is a triangle that has two sides of equal length and two angles of equal measure. The two equal sides are known as the legs, and the angle opposite the base is known as the vertex angle.
A right triangle, on the other hand, is a triangle that has one right angle (an angle measuring 90 degrees). In a right triangle, the side opposite the right angle is the longest side and is called the hypotenuse.
While it is possible for an isosceles triangle to be a right triangle, it is not a requirement. In an isosceles triangle, the vertex angle can be acute (less than 90 degrees) or obtuse (greater than 90 degrees). Only if the vertex angle of an isosceles triangle measures 90 degrees, then it becomes a right isosceles triangle.
Learn more about isosceles triangles at:
https://brainly.com/question/1475130
#SPJ4
What does the 14th Amendment mean ?.
Answers
Can someone pls help meeeeeee!!!

Answers
Answer:
For question 2, Ethan needs 3 cups of milk to make the batter for 3 times as many cakes.
For question 3, Isabella needs 5/4 of a gallon of the food to make 5 gallons of the mixture.
The International Air Transport Association surveys business travelers to develop quality ratings for transatlantic gateway airports. The maximum possible rating is 10. Suppose a simple random sample of 50 business travelers is selected and each traveler is asked to provide a rating for the Miami International Airport. The ratings obtained from the sample of 50 business travelers follow.
1 5 6 7 8 8 8 9 9 9 9 10 3 4 5 5 7 6 8 9 10 5 4 6 5 7 3 1 9 8 8 9 9 10 7 6 4 8 10 2 5 1 8 6 9 6 8 8 10 10
Develop a 95% confidence interval estimating of the population mean rating for Miami.
Answers
CI = 6.76 ± 1.96 × (2.67/√50)
CI = 6.76 ± 0.96
Therefore, the 95% confidence interval for the population means rating for Miami is: (5.80, 7.72)
We can be 95% confident that the true mean rating for Miami International Airport falls within this interval.
To develop a 95% confidence interval for the population means rating for Miami International Airport, we need to follow these steps:
1. Calculate the sample mean (x) by adding up all the ratings and dividing by the sample size (n=50).
2. Calculate the sample standard deviation (s).
3. Use a t-distribution to find the t-score for a 95% confidence interval with (n-1) degrees of freedom.
4. Calculate the margin of error (ME) using the t-score, standard deviation, and sample size.
5. Add and subtract the margin of error from the sample mean to find the lower and upper limits of the confidence interval.
To calculate the 95% confidence interval, we need to use the formula:
CI = x ± Z' (s/√n)
Where:
x = sample mean
Z' = z-score for the desired confidence level (in this case, 95%, so
Z' = 1.96)
s = sample standard deviation
n = sample size
Step 1: Calculate the sample mean (x)
Sum of ratings = 346
Sample size (n) = 50
x = 346/50 = 6.92
Step 2: Calculate the sample standard deviation (s)
Variance = [(Sum of (rating - x)^2) / (n-1)] = 88.48
Standard deviation (s) = √(88.48) = 9.41
Step 3: Find the t-score
For a 95% confidence interval with 49 (n-1) degrees of freedom, the t-score is approximately 2.01.
Step 4: Calculate the margin of error (ME)
ME = t-score × (s / √n) = 2.01 × (9.41 / √50) = 2.01 × 1.33 = 2.67
Step 5: Find the confidence interval
Lower limit: x - ME = 6.92 - 2.67 = 5.80
Upper limit: x + ME = 6.92 + 2.67 = 7.72
Thus, the 95% confidence interval for the population mean rating for Miami International Airport is approximately
(5.80, 7.72)
Learn more about confidence intervals:
brainly.com/question/24131141
#SPJ11
Express the formula d=rt in terms of the time,t. Use your formula to find the time when the distance is 40 and the rate is 8.
Answers
The expression for d=rt in terms of the time is t = d/r; t = 5.
What is time? Time can be defined as a continuous and ongoing sequence of events that occur consecutively from the past to the present to the future. Time is used to measure, measure or compare the duration of events or the intervals between them, and even the sequence of events. Time is a useful concept that we use in our daily life. We have to watch when we cook, play, study, go to school, meet someone, etc. So knowing the right time is very important. Time is usually the answer to when an event happens or happened. The concept of time determines when a certain event occurs, has occurred or will occur. Time is a measurable quantity and is also infinite. The time is calculated in seconds, minutes, hours, days, months and years.Therefore,
In the equation d=rt
t = d/r
when distance is 40 and the rate is 8
t = d/r
Replace d with 40 and rate with 8
t = 40/8
t = 5
To learn more about time, refer;
https://brainly.com/question/28050940
#SPJ1
why solids are important?
Answers
Answer:
Solids can hold their shape because their molecules are tightly packed together. ... Atoms and molecules in liquids and gases are bouncing and floating around, free to move where they want. The molecules in a solid are stuck in a specific structure or arrangement of atoms.
I hope you find this helpful.
URGENT PLEASE HELP
x/240 = 82/100 what is X?
Answers
x/240 = 82/100
240 : 100 = 2.4
so 240 is divided with 2,4 giving 100, this will work with 82 too. So, 82 × 2.4 = 196,8
Answer : x = 196,8
prove :
196,8/240 = 82/100 = 41/50
see the picture

t-1/4=3/4 please help super confusing
Answers
Answer:
T=1 i think
Step-by-step explanation:
25 points plus brainliest
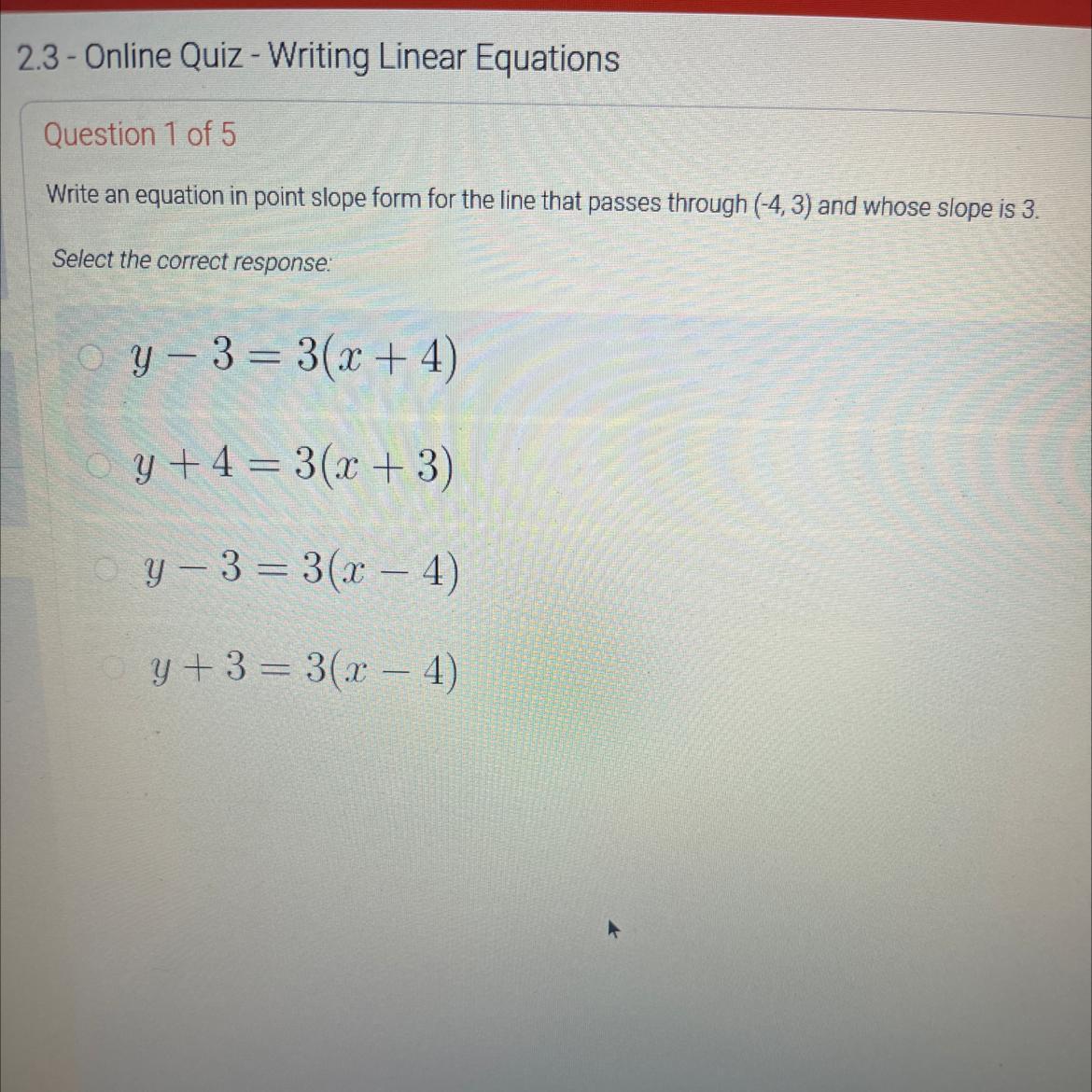
Answers
Answer: y-3 = 3(x+4)
Step-by-step explanation:
See attached

patients scheduled to see their primary care physician at a particular hospital wait, on average, an additional ten minutes after their appointment is scheduled to start. assume the time that patients wait is exponentially distributed. what is the probability a randomly selected patient will see the doctor within fourteen minutes of the scheduled time?
Answers
Therefore , the solution of the given problem of probability comes out to be 59.3% chance that an arbitrarily chosen patient will see the doctor within 14 minutes of the appointment time.
What precisely is probability?The determination of the likelihood that an assertion is accurate or that a particular event will occur is the main objective of the systems within the process known as criteria. Chance can be represented by any number between 0 and 1, where 0 is frequently used to indicate that it's possible and 1 is frequently used to signify a degree of confidence. A probability diagram shows the likelihood that a particular occurrence will occur.
Here,
With a mean of 10 minutes and an exponential distribution, X has the following probability density function:
=> For x >= 0, f(x) = (1/10) * e(-x/10).
The likelihood that an arbitrarily chosen patient will see the doctor within 14 minutes of the appointment time is what we are trying to determine. This can be stated as follows:
=> P(X <= 14)
Integrate the density function from 0 to 14 to discover this probability:
=> P(X = 14) = e(-x/10) * [0,14] (1/10)
=> P(X = 14) = 0 1.4 e (-u) du
The integral's evaluation yields:
=> P(X <= 14) = [\(-e^{-u}\)] between 0 and 1.4
=> P(X <= 14) = -e⁻¹⁴ + 1
=> P(X <= 14) ≈ 0.593
This means that there is a 59.3% chance that an arbitrarily chosen patient will see the doctor within 14 minutes of the appointment time.
To know more about probability visit:
https://brainly.com/question/11234923
#SPJ1
1. Two adjacent angles
2. Two acute vertical angles
3. Two obtuse vertical angles

Answers
Answer: D e acute
Step-by-step explanation:
Prove the identity of each of the following Boolean equations, using algebraicmanipulation:Manipulation: (a) ABC + BCD + BC + CD = B + CD (b) WY + WYZ + WXZ + WXY = WY + WXZ + XYZ + XYZ (c) AD + AB + CD + BC = (A + B + C + D)(A + B + C + D)
Answers
a) The simplified left-hand side of the equation as B + CD + BD. Therefore, the equation is true. b) The simplified left-hand side of the equation as 2WY + WXZ + WYZ. Therefore, the equation is true. c) The left-hand side of the equation is also AD + AB + CD + BC, the equation is true.
(a) Using algebraic manipulation, we can simplify the left-hand side of the equation as follows:
ABC + BCD + BC + CD = BC(A + D) + CD(A + B)
= BC + CD (A + B + D)
Since B + CD = B(1 + D) + CD = B + CD + BD, we can rewrite the simplified left-hand side of the equation as B + CD + BD. Therefore, the equation is true.
(b) Similarly, we can simplify the left-hand side of the equation as follows:
WY + WYZ + WXZ + WXY = WY(1 + Z) + WX(Z + Y)
= WY + WXZ + WYZ + XYZ
Since WY + WXZ + XYZ = WY + WXZ + WY(1 + Z) = WY + WXZ + WY + WYZ = 2WY + WXZ + WYZ, we can rewrite the simplified left-hand side of the equation as 2WY + WXZ + WYZ. Therefore, the equation is true.
(c) Using algebraic manipulation, we can expand the right-hand side of the equation as follows:
(A + B + C + D)(A + B + C + D) = A2 + B2 + C2 + D2 + AB + AC + AD + BC + BD + CD
= AD + AB + CD + BC + A2 + B2 + C2 + D2 + AB + AC + BD
= AD + AB + CD + BC (A + B + C + D + A + B + C + D)
Since the left-hand side of the equation is also AD + AB + CD + BC, the equation is true.
Learn more about algebraic manipulation here:
https://brainly.com/question/12602543
#SPJ11
Need help for one question for geometry !

Answers
2x+3y = 1 and 7x+2y = -22 by elimination
Answers
The solution to the given system of linear equations 2x + 3y = 1 and 7x + 2y = -22 by elimination is (-4, 3). That is, x = -4 and y = 3.
Solving system of linear equations by elimination methodFrom the question, we are to solve the given system of linear equation by the elimination method.
To solve the system of equations 2x + 3y = 1 and 7x + 2y = -22 by elimination, we can multiply the first equation by 2 and the second equation by -3 to eliminate the x variable:
(2)(2x + 3y = 1) ⇒ 4x + 6y = 2
(-3)(7x + 2y = -22) ⇒ -21x - 6y = 66
Adding the two resulting equations gives:
-17x = 68
Dividing both sides by -17 gives:
x = -4
Now we can substitute this value of x into one of the original equations to solve for y. Let's use the first equation:
2x + 3y = 1
2(-4) + 3y = 1
-8 + 3y = 1
3y = 9
y = 3
Hence, the solution is x = -4 and y = 3
Learn more on Solving system of linear equations here: https://brainly.com/question/28405823
#SPJ1
4 quick algebra 1 questions for 50 points!
Only answer if you know the answer, shout-out to subtomex0, tysm for the help!




Answers
\(c(g) = 7g + 52 \\ c(0) = 52\)
Option CQuestion 2\(g(x) = x {}^{2} - 7x + 12 \\ g(x) = 0 \\ x = 3 \: \: \: \: \: \: \: \: x = 4\)
Option DQuestion 1Option CLet's see
#1
y=2x²+3x-2y=2x²+4x-x-2y=(x+2)(2x-1)So
x intercepts
(-2,0) and (1/2,0)True
#2
y=7g+52y=7(0)=52y=52Option C
#3
x²-7x+12=0x²-4x-3x+12=0x(x-4)-3(x-4)=0(x-3)(x-4)=0x={3,4}Option D
#4
I solved it in your another question , Can't add that answer here due to copyright restrictions
Answer the following questions. "Proof by Venn diagram" is not an acceptable approach. Remember that mathematics is a language, and it is necessary to use correct grammar and notation. 1. If A and B are ANY two sets, determine the truth-values of the following statements. If a statement is false, give specific examples of sets A and B that serve as a counter- example (3 pts each). a. (A\B) CA b. Ac (AUB)
Answers
In this question, we are asked to determine the truth-values of two statements involving sets A and B. For each statement, we need to determine if it is true or false. If it is false, we need to provide specific counterexamples by choosing appropriate sets A and B.
a. (A\B) ⊆ A
The statement (A\B) ⊆ A is true for any sets A and B. This is because the set difference (A\B) contains elements that are in A but not in B. Therefore, by definition, every element in (A\B) is also an element of A. There are no counterexamples to this statement.
b. A^c ⊆ (AUB)
The statement\(A^c\) ⊆ (AUB) is true for any sets A and B. This is because the complement of A, denoted as \(A^c\), contains all elements that are not in A.
On the other hand, the union of A and B, denoted as (AUB), contains all elements that are in A or in B or in both.
Since the complement of A contains all elements not in A, it includes all elements in B that are not in A as well.
Therefore, \(A^c\) ⊆ (AUB) holds true for any sets A and B. There are no counterexamples to this statement.
In conclusion, both statements are true for any sets A and B, and there are no counterexamples.
To learn more about sets visit:
brainly.com/question/30705181
#SPJ11
personnel tests are designed to test a job applicant's cognitive and/or physical abilities. a particular dexterity test is administered nationwide by a private testing service. it is known that for all tests administered last year, the distribution of scores was approximately normal with mean and standard deviation . a. a particular employer requires job candidates to score at least on the dexterity test. approximately what percentage of the test scores during the past year exceeded ? b. the testing service reported to a particular employer that one of its job candidate's scores fell at the th percentile of the distribution (i.e., approximately % of the scores were lower than the candidate's, and only % were higher). what was the candidate's score?
Answers
a. percentage of the test scores during the past year exceeded 83 is approximately 26.11%.
b. the candidate's score is approximately 90.32
a. To determine the percentage of test scores that exceeded 83, we need to calculate the area under the normal distribution curve above the score of 83.
First, we need to standardize the score by calculating the z-score. The formula for the z-score is:
z = (x - μ) / σ
where x is the raw score, μ is the mean, and σ is the standard deviation.
In this case, x = 83, μ = 78, and σ = 7.8.
z = (83 - 78) / 7.8
z = 0.64
Using a standard normal distribution table or calculator, we can find the percentage of scores above a z-score of 0.64. The table or calculator will provide the area under the curve to the left of the z-score, so we subtract that from 1 to get the area to the right (above) of the z-score.
Approximately 1 - 0.7389 = 0.2611
Therefore, approximately 26.11% of the test scores during the past year exceeded 83.
b. The 95th percentile indicates that the candidate's score is higher than 95% of the scores in the distribution. To find the candidate's score, we need to find the z-score corresponding to the 95th percentile.
Using a standard normal distribution table or calculator, we can find the z-score that corresponds to a cumulative area of 0.95. In other words, we need to find the z-score such that 95% of the area under the curve is to the left of it.
The z-score corresponding to a cumulative area of 0.95 is approximately 1.645.
Now, we can use the z-score formula to find the candidate's score:
z = (x - μ) / σ
Rearranging the formula:
x = μ + (z * σ)
x = 78 + (1.645 * 7.8)
x ≈ 90.32
Therefore, the candidate's score is approximately 90.32.
Know more about the percentage here:
https://brainly.com/question/24877689
#SPJ8
The question is incomplete. Find the full content below:
Personnel tests are designed to test a job applicant's cognitive and/or physical abilities. A particular dexterity test is administered nationwide by a private testing service. It is known that for all tests administered last year, the distribution of scores was approx. normal with a mean of 78 and a standard deviation7.8.
a. A particular employer requires job candidates to score at least 83 on the dexterity test. Approximately what percentage of the test scores during the past year exceeded 83?
b. The testing service reported to a particular employer that one of its job candidate's scores fell at the 95h percentile of the distribution. (approx 95% of the scores were lower than the candidate's, and only 5% were higher) What is the candidate's score?
answerrrrrr plssss ill giveee brainliesttttt

Answers
\(m\angle E=\sin \dfrac{\sqrt{10}}{2\sqrt5}=\sin \dfrac{\sqrt2}{2}=45^{\circ}\)
it is believed that 5% of all people requesting travel brochures for transatlantic cruises actually take the cruise within 1 year of the request. an experienced travel agent believes this is wrong. of 100 people requesting one of these brochures, only 3 have taken the cruise within 1 year. we want to test the travel agent's theory with a hypothesis test. if you used a significance level of 0.05, what is your decision?
Answers
Based on the given information, we can set up the following hypotheses for the hypothesis test:
Null Hypothesis (H0): The actual proportion of people taking the cruise within 1 year is equal to the believed proportion of 5%.
Alternative Hypothesis (H1): The actual proportion of people taking the cruise within 1 year is not equal to the believed proportion of 5%.
Let p be the proportion of people taking the cruise within 1 year. We can use the sample proportion, denoted as p-hat, which is calculated as the ratio of the number of people who took the cruise within 1 year (3 in this case) to the total number of people who requested the brochures (100 in this case).
Given that the significance level is 0.05, we can use a z-test to compare the sample proportion with the believed proportion of 5%. The z-test statistic is calculated as:
z = (p-hat - p) / sqrt(p * (1 - p) / n)
where n is the sample size, which is 100 in this case.
Now we can calculate the z-test statistic and compare it with the critical value for a two-tailed test at a significance level of 0.05. If the calculated z-test statistic falls outside the critical value, we would reject the null hypothesis; otherwise, we would fail to reject the null hypothesis.
Since the sample proportion p-hat is 3/100 = 0.03, and the believed proportion p is 0.05, we can substitute these values into the z-test formula:
z = (0.03 - 0.05) / sqrt(0.05 * (1 - 0.05) / 100)
Calculating the above expression, we get the value of z. We can then compare this value with the critical value for a two-tailed test at a significance level of 0.05 from a standard normal distribution table or using a statistical calculator.
If the calculated z-test statistic falls outside the critical value, we would reject the null hypothesis and conclude that the actual proportion of people taking the cruise within 1 year is different from the believed proportion of 5%. If the calculated z-test statistic falls within the critical value, we would fail to reject the null hypothesis and not conclude that the actual proportion is different from the believed proportion.
Without the actual values of the calculated z-test statistic and the critical value, we cannot provide a specific decision for this hypothesis test. Please note that hypothesis testing requires careful consideration of the sample size, significance level, and other relevant factors, and should be conducted with caution and in consultation with a qualified statistician or expert in statistical analysis.
i need help with this question parts c d and e


Answers
SOLUTION
(c) The values of x for which f(x) = -1
Looking from the graph, this does not exist.
Hence the answer is "None"
(d) The values of x for which f(x) = -3
Looking form the graph, this is between 0 and 1
So we have this as
\(0\leq x<1\)So in interval notation, the answer is
\([0,1)\)(e) The x-intercept is where the graph cuts the x-axis
The graph cuts the x-axis at -1
Hence the answer is (-1, 0)
What is the answer to this question?

Answers
Answer:
≈ 3.9 miles
Step-by-step explanation:
The third angle in the triangle is
180° - (53 + 78)° = 180° - 131° = 49°
Using the Sine rule in the triangle with distance from 2 being x, then
\(\frac{3}{sin49}\) = \(\frac{x}{sin78}\) ( cross- multiply )
x × sin49° = 3 × sin78° ( divide both sides by sin49° )
x = \(\frac{3sin78}{sin49}\) ≈ 3.9 ( to the nearest tenth )
How much water in mL) is needed to prepare a 0.64 M KCl solution from 83 mL of a 2.23M KCl solution? Write answer in decimal form to one decimal places. no units
Answers
The amount of water in mL required to prepare a 0.64 M KCl solution from 83 mL of a 2.23M KCl solution is 206.2 mL.
To prepare a 0.64 M KCl solution from 83 mL of a 2.23 M KCl solution, you will need to use the dilution formula:
M1V1 = M2V2,
where M1 is the initial concentration, V1 is the initial volume, M2 is the final concentration, and V2 is the final volume.
1. Rearrange the formula to find V2: V2 = M1V1 / M2
2. Substitute the given values into the formula: V2 = (2.23 M * 83 mL) / 0.64 M
3. Perform the calculations: V2 = (185.09 mL) / 0.64 M
4. Calculate the final volume: V2 = 289.2 mL
Now, we need to find how much water should be added to reach this final volume. Subtract the initial volume from the final volume: 289.2 mL - 83 mL = 206.2 mL.
Therefore, 206.2 mL of water is needed to prepare a 0.64 M KCl solution from 83 mL of a 2.23 M KCl solution.
Learn more about KCl:
https://brainly.com/question/29014138
#SPJ11
What is the value of (2/3−1/9)×4 cubed −5/9?
Answers
Answer:
14/9
Step-by-step explanation:
Answer:
The answer is 35!
Step-by-step explanation:
I got it wrong and it gave me the answer.
Josiah plants vegetable seeds in rows. Each row has the same number of seeds in it. He plants more than one row of seeds. What could be the total number of seeds he plants?
Answers
The total number of seeds that Josiah would plant would be = nR×S
How to determine the total number of seeds that Josiah will plant?To determine the total number of seeds that Josiah will plant will be to add the seeds in the total number of rooms he planted.
Let each row be represented as = nR
Where n represents the number of rows planted by him.
Let the seed be represented as = S
The total number of seeds he planted = nR×S
Therefore, the total number of seeds that was planted Josiah would be = nR×S.
Learn more about multiplication here:
https://brainly.com/question/30340107
#SPJ1
el producto de dos números es 324. si cada uno de esos números se multiplica por 3¿cuál es el nuevo producto?
Answers
Answer:
672 cre o rectifica porfa
Answer:
108 y 3
Step-by-step explanation:
si multiplicamos 108×3 nos da
=324
y 108 y 3 son divisibles o multiplicados por 3
please help i need y intercept and slope

Answers
Answer:
slope: 1 /8
y-intercept: ( 0 , − 1 /4 )

If you vertically compress the absolute value parent function, f(x) =|x|, by a factor of 5, what is the equation of the new function?
Answers
Answer:
g(x) = 1/5 |x|
Step-by-step explanation:
Answer:
g(x) = (1/5)|x|
Step-by-step explanation:
Vertical stretch/compression is achieved by multiplying the function by a certain constant:
In particular, if the function is vertically stretched by a factor k, otherwise, if , the function is vertically compressed by a factor k.
So, in your case, you want to multiply the function by 1/5:
|x|->(1/5)|x|
A school bought 32 new desks. Each desk cost $24. Estimate how much the school spent on the new desks
Answers
Answer:
768 dollars
Step-by-step explanation:
у
Which function is represented by the graph?
A- f(x)= -2|x| + 1
B- f(x)= - 1/2|x| + 1
C- f(x)= -2|x + 1|
D- f(x)= - 1/2|x + 1|

Answers
For which function defined by a polynomial, are the zeros of the polynomial -2 and -7?
Answers
Answer:
Step-by-step explanation:
f(x)=a(x+2)(x+7)=a(x²+2x+7x+14)
or f(x)=a(x²+9x+14)
it has zeros as -2 and -7.