consider the expression 3 * 2 ^ 2 < 16 5 andalso 100 / 10 * 2 > 15 - 3. which operation is performed first?
Answers
In the given expression, the multiplication and division operations are performed first, followed by any addition and subtraction operations.
To evaluate the given expression, we need to break it down into individual operations and then apply the order of operations. Let's analyze each operation step by step:
Parentheses: In this expression, there are no parentheses, so we can skip this step.
Exponents: The exponentiation operation is denoted by the "^" symbol. However, in this expression, there are no exponents.
Multiplication and Division: The multiplication and division operations are performed from left to right. In the given expression, we have two multiplication operations: "\(3 * 2 ^ 2\)" and "100 / 10 * 2." According to the order of operations, we need to evaluate these multiplications before moving on to other operations.
First, let's consider "\(3 * 2^2\)" In this case, the exponentiation operation (^) takes precedence over multiplication. Therefore, we need to evaluate "\(2^2\)" first. Since 2 raised to the power of 2 is 4, the expression becomes "3 * 4."
Next, we have "100 / 10 * 2." As there are no other operations to perform before division, we can proceed with evaluating this expression. The division of 100 by 10 results in 10, and then multiplying by 2 gives us 20.
Addition and Subtraction: The addition and subtraction operations are also performed from left to right. In the given expression, we have "16 5" and "15 - 3" as the remaining operations.
Let's consider "16 5" first. The expression "16 5" is ambiguous because there is no operator between the numbers. It is essential to have a proper operator like ">" or "<" to determine the relationship between the two numbers. Without it, the expression is invalid.
Finally, we have "15 - 3." Subtracting 3 from 15 gives us 12.
Now that we have evaluated each operation, we can rewrite the expression as "3 * 4 < 12 and also 20 > 12."
To summarize, the operations are performed in the following order:
Exponents (if any)
Multiplication and Division (from left to right)
Addition and Subtraction (from left to right)
To know more about expression here
https://brainly.com/question/14083225
#SPJ4
Related Questions
Triangle ABC can be plotted at A (-14, 14), B (-8, 11) & C (-14, 5). Reflect Triangle ABC acro the y-axi. Next, rotate 180 degree counterclockwie about the origin. What i the ordered pair of C'' after the equence of tranformation?
Answers
The ordered pair of C'' after the sequence of transformation is (-14, -5)
Here we have know that ABC can be plotted at A (-14, 14), B (-8, 11) & C (-14, 5).
Here we all know that the y-axis reflection rule is written as,
=> (x, y) → (-x, y)
And the value of x coordinate flips in sign from positive to negative, or vice versa. Then the value of y coordinate stays the same.
Then the point is look like C(-14,5) will then reflect based on the following rule,
=> (x, y) → (x, y)
The transformed coordinates are look like,
=> (-14,5) ((-14),5)
=> (-14,5)→ (14,5)
Therefore, here we have point C' located at (14,5) after applying the y-axis reflection rule on point C.
Now, the next operation to do is is the 180 degree rotation.
And this can be clockwise or counterclockwise.
Then the rotation rule is written as
=> (x, y) → (-x,y)
Now, for this time both coordinates flip in sign.
Here we have know that this rule only works if the center of rotation is the origin.
Now, let us apply that rotation rule to C' to find where C" is located.
Then the rule can be written as, (x, y) → (-x,y)
=> (14,5)→ (-14, -5)
To know more about Coordinates here.
https://brainly.com/question/27749090
#SPJ4

What is the formula for sin and cos?
Answers
The formula for sin and cos are opposite side/hypotenuse and adjacent side/hypotenuse respectively.
Sin and Cos formulae are based on the sides of the right-angled triangle. Along with the tan function, the fundamental trigonometric functions in trigonometry are sin and cos. In contrast to the cosine of an angle, which corresponds to the ratio of the adjacent side to the hypotenuse, the sine of an angle is the ratio of the opposing side to the hypotenuse.
Sine of an angle θ = opposite side/hypotenuse
Cosine of an angle θ = adjacent side/hypotenuse
The figure given in the attachment is a right angled triangle which shows opposite side, adjacent side and hypotenuse side with an angle θ which is specified.
To know more about angles:
https://brainly.com/question/84236
#SPJ4

Is the following number rational or irrational?
13
12
Choose 1 answer:
А
Rational
B
Irrational

Answers
Answer: Rational
This is because the number is in the form P/Q where P and Q are integers
We have P = -13 and Q = 12.
You can think of "rational" as in "ratio" which is very closely tied to fractions. Any rational number is a fraction of two integers. The denominator can never be zero.
Answer:
Rational
Step-by-step explanation:
A rational number is any integer, fraction, terminating decimal, or repeating decimal.
Decimal form: − 1.08 3
3 repeats itself, so it's rational.
Connor is a 400m runner His median time is
Answers
Answer: 57.8
Step-by-step explanation:48.7 seconds + 49.3 seconds.= 57.8
what is the probability that a randomly selected cereal box weighs at most 19.4 ounces?
Answers
Answer:
Step-by-step explanation:

3. Kerry goes to a gym and pays a $200
membership fee each year. She also
pays $40 for each class she enrolls in. If
she has spent $480. how many classes
has Kerry enrolled in?
how would i do this ?
Answers
Answer: 7 classes enrolled in
Step-by-step explanation:
200+40n=480
40n = 280
n = 7
Find the percent of the octagon that is shaded in

Answers
Explanation:
We have 5 slices shaded out of 8 total. Therefore, we have 5/8 = 0.625 = 62.5% of this figure is shaded.
Answer:
62.5%
Step-by-step explanation:
Help me! I'm lost!
The wall in in the shape of a rectangle. The wall is 3m wide and 2.5m high. .The tiles are rectangles 20cm wide and 25cm high. The tiles are sold in boxes. There are 20 tiles in each box. Each box of tiles costs £8.50.
Work out the total cost of the boxes of tiles Andy needs to buy.
You must show all your working.
Answers
Answer:
£68
Step-by-step explanation:
Width of wall = 3m = 300 cmHeight of wall = 2.5m = 250 cm
Width of one tile = 20cm
Calculate how many tiles you need to fit the width of the wall:
width of wall ÷ width of tile = 300 ÷ 20 = 15 tiles wide
Height of one tile = 25cm
Calculate how many tiles you need to fit the height of the wall:
height of wall ÷ height of tile = 250 ÷ 25 = 10 tiles high
Therefore, total tiles needed = 15 x 10 = 150 tiles
If there are 20 tiles in each box,
total tiles ÷ 20 = 150 ÷ 20 = 7.5 boxes
So we need to round this UP to 8 boxes (else we won't have enough tiles)
Therefore, 8 boxes of tiles at £8.50 per box:
Total cost = 8 x 8.50 = £68
How do you dilate a triangle with a scale factor of 2 3?
Answers
The basic formula to find the scale factor of a dilated figure is: Scale factor = Dimension of the new shape ÷ Dimension of the original shape.The dilation o a triangle with a scale factor of 2 3 represents a contraction.
How to Dilate a triangle with a scale factor ?
The scale factor is defined as the proportion of the new image's size to that of the previous image. A fixed location in the plane serves as the centre of dilatation. The scale factor and the centre of dilation are used to determine the dilation transformation.
The image stretches if the scaling factor is greater than 1.The image contracts if the scale factor is between 0 and 1.The original image and the resulting image are consistent if the scale factor is 1.Finding the dilation's centre point is the first step in determining the scale factor. Next, we measure the distances between the centre point and various points on the preimage and the image. According to Math Bits Notebook, the scale factor is equal to the ratio of these distances.
Since each angle is congruent, every segment is proportional, the slope of every segment is preserved, and the perimeter of the preimage and image have the same scale factor, we may use dilation scale factors to compress or enlarge a figure to the size we desire.
Dilate a triangle with a scale factor
Assume that the coordinate plane's centre of dilation is at (0, 0) at the origin. Every coordinate point of the original triangle is multiplied by the scale factor 2/3 if the scale factor is 2/3. multiplying by half after a scale factor of two.
To know more about How to Dilate a triangle with a scale factor, Refer to:
https://brainly.com/question/29793517
#SPJ4
pls pls pls helpjust need the answer

Answers
Answer:
k = - 8
Step-by-step explanation:
given that (x - a) is a factor of f(x) , then f(a) = 0
given
(x - 1) is a factor of f(x) then f(1) = 0 , that is
3(1)³ + 5(1) + k = 0
3(1) + 5 + k = 0
3 + 5 + k = 0
8 + k = 0 ( subtract 8 from both sides )
k = - 8
For the following right triangle, find the side length A15 B20
Answers
Answer:
Step-by-step explanation:
you first take A15 and square it. Then you take B20 and square it also. Then you add them together and that is your answer. the hypotenuse of a triangle.
Answer: Side length C will be 25
Step-by-step explanation:
C^2 = A^2+B^2
15^2+20^2=C^2
225+400=625
Take square root of 625 to get side C
A soccer player has a large cylindrical water cooler that measures 2.5 feet in diameter and is 5 feet tall. If there are approximately 7.48 gallons of water in a cubic foot, how many gallons of water are in the water cooler when it is completely full? Use π = 3.14 and round to the nearest hundredth.
98.13 gallons
733.98 gallons
24.53 gallons
183.49 gallons
Answers
The volume in gallons of the water cooler is 183.49 gallons
How many gallons of water are in the water cooler when it is completely full?We know that the volume of a cylinder of radius R and height H is.
V = pi*R²*H
Where pi = 3.14
Here we know that the diameter is 2.5 ft, then the radius is:
R = 2.5ft/2 = 1.25ft
And the height is 5ft
So the volume is:
V = 3.14*(1.25ft)²*5ft = 24.53125 ft³
And we know that
1ft³ = 7.48 gallons
Then we can do a change of units to get:
24.53125*7.48 gal = 183.49 gal
That is the correct option.
Learn more about volume at:
https://brainly.com/question/1972490
#SPJ1
Show the family of conics with the same focus
x^2/a^2+C + y^2/b^2+C = 1
is its own orthogonal family of curves.
Answers
The original equation and the orthogonal equation are the same, we can conclude that the family of conics with the same focus x^2/a^2+C + y^2/b^2+C = 1 is its own orthogonal family of curves.
To show that the family of conics with the same focus x^2/a^2+C + y^2/b^2+C = 1 is its own orthogonal family of curves, we need to take the derivative of the equation and set it equal to -1/b^2, the slope of the orthogonal line.
First, we take the derivative of the equation with respect to x:
2x/a^2 = -2y/b^2 * dy/dx
Simplifying, we get:
dy/dx = -b^2*x/a^2*y
Now, we set this equal to -1/b^2:
-b^2*x/a^2*y = -1/b^2
Cross-multiplying and simplifying, we get:
x/a^2*y = 1/b^2
Finally, we can rearrange this equation to get:
y = b^2*x/a^2
This equation represents the orthogonal family of curves to the original family of conics. Since the original equation and the orthogonal equation are the same, we can conclude that the family of conics with the same focus x^2/a^2+C + y^2/b^2+C = 1 is its own orthogonal family of curves.
Learn about Conics
brainly.com/question/29767685
#SPJ11
Lotteries In a New York State daily lottery game, a sequence of two digits (not necessarily different) in the range 0-9 are selected at random. Find the probability that both are different.
Answers
The probability that both digits in a New York State daily lottery game are different is 0.9, or 9 out of 10.
To find the probability that both digits in a New York State daily lottery game are different, we need to first calculate the total number of possible outcomes. Since there are 10 digits (0-9) that can be selected for each of the two digits in the sequence, there are a total of 10 x 10 = 100 possible outcomes.
Now, we need to determine the number of outcomes where both digits are different. There are 10 possible choices for the first digit and only 9 possible choices for the second digit, since we cannot choose the same digit as the first. Therefore, there are a total of 10 x 9 = 90 outcomes where both digits are different.
The probability of both digits being different is equal to the number of outcomes where both digits are different divided by the total number of possible outcomes. Thus, the probability is 90/100, which simplifies to 9/10, or 0.9.
In summary, the probability that both digits in a New York State daily lottery game are different is 0.9, or 9 out of 10. This means that there is a high likelihood that both digits selected will be different.
To know more about probability, refer to the link below:
https://brainly.com/question/13941450#
#SPJ11
Click an item in the list or group of pictures at the bottom of the problem and, holding the button down, drag it into the correct position in the answer box. Release your mouse button when the item is place. If you change your mind, drag the item to the trashcan. Click the trashcan to clear all your answers.
Complete the following proof.
Given: RS tangent to circle A and circle B
at points R and S
Prove: AR parallel to BS


Answers
Step-by-step explanation:
Statements
1.RS tangent to circle A and circle B at point R and point S
2.AR is perpendicular to RS, BS is perpendicular to RS
3.AR is parallel to BS
Reasons
1.Given
2.Radius are perpendicular to tangent
3. 2 lines perpendicular to the same line are parallel to each other
Formalize the following in terms of atomic propositions r, b, and w, first making clear how they correspond to the
English text. (a) Berries are ripe along the path, but rabbits have not been seen in the area.
(b) Rabbits have not been seen in the area, and walking on the path is safe, but berries are ripe along the path.
(c) If berries are ripe along the path, then walking is safe if and only if rabbits have not been seen in the area.
(d) It is not safe to walk along the path, but rabbits have not been seen in the area and the berries along the path are ripe.
e) For walking on the path to be safe, it is necessary but not sufficient that berries not be ripe along the path and for rabbits not to
pave been seen in the area.
Walking is not safe on the path whenever rabbits have been seen in the area and berries are ripe along the path.
Answers
Walking is not safe on the path whenever rabbits have been seen in the area, and berries are ripe along the path. This is formalized by using the →(if-then) and ∧(logical and) operators.
Given information and corresponding atomic propositions:
We need to formalize the given statements in terms of atomic propositions r, b, and w, which are defined as follows:
r: Rabbits have been seen in the area.
b: Berries are ripe along the path.
w: Walking on the path is safe.
Now, let us formalize each of the given statements in terms of these atomic propositions:
a) Berries are ripe along the path, but rabbits have not been seen in the area.
b: Rabbits have not been seen in the area, and walking on the path is safe, but berries are ripe along the path.
c: If berries are ripe along the path, then walking is safe if and only if rabbits have not been seen in the area.
d: It is not safe to walk along the path, but rabbits have not been seen in the area, and the berries along the path are ripe.
e) For walking on the path to be safe, it is necessary but not sufficient that berries not be ripe along the path and for rabbits not to have been seen in the area.
Walking is not safe on the path whenever rabbits have been seen in the area, and berries are ripe along the path.
The formalizations in terms of atomic propositions are:
a) b ∧ ¬r.b) ¬r ∧ w ∧
b.c) (b → w) ∧ (¬r → w).
d) ¬w ∧ ¬r ∧
b.e) (¬r ∧ ¬b) → w.b ∧
Berries are ripe along the path, but rabbits have not been seen in the area.
This is formalized by using the ∧(logical and) operator.
(¬r ∧ ¬b) → w: It means For walking on the path to be safe, it is necessary but not sufficient that berries not be ripe along the path and for rabbits not to have been seen in the area.
For more related questions on area:
https://brainly.com/question/1631786
#SPJ8
Carla has a rectangular garden in her backyard. The width of the garden is 9 meters. The area of the garden is 360 square meters. What is the length of the garden? Show your work.
Answers
Answer:
l = 40 m
Step-by-step explanation:
The formula for area of a rectangle is
A = lw, where
A is the area in square units,l is the length,and w is the widthStep 1: Since we're given the area and width, we plug in these two values for A and w and to solve for l (length):
360 = 9l
Step 2: Divide both sides by 9 to solve for l
(360 = 9l) / 9
40 m = l
Optional Step 3: We can check our answers by checking that the product of 40 and 9 is 360
40 * 9 = 360
360 = 360
When a number is increased by 5.5%, the result is 60. What is the original number to the nearest tenth?
Answers
Answer: 56.9
Step-by-step explanation:
Let the original number be denoted by x.
We are informed that when the number is increased by 5.5%, the result is 60. This can be represented by:
x + (5.5% of x) = 60
x + (0.055 × x) = 60
x + 0.055x = 60
1.055x = 60
x = 60/1.055
x = 56.9
The original number is 56.9
Find the mean for the data set. 6, 14, 7, 4, 12, 8, 13, 4, 18, 14
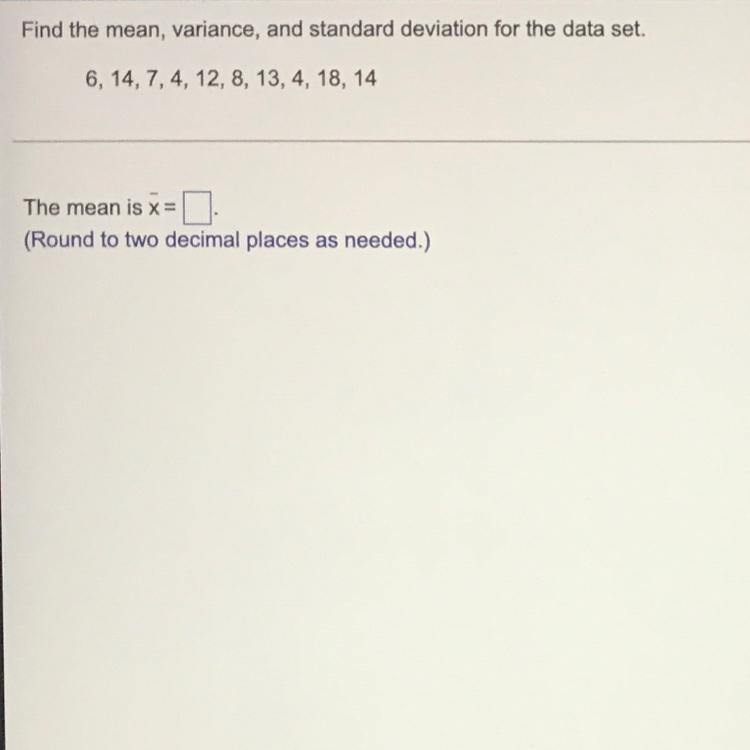

Answers
Answer:
Concept:
Mean is just another name for average. To find the mean of a data set, add all the values together and divide by the number of values in the set. The result is your mean!
The values are given below as
\(6,14,7,4,12,8,13,4,18,14\)The image below shows how to calculate the mean
By substituting values, we will have
\(\begin{gathered} \bar{x}=\frac{\sum ^{}_{n\mathop=0}x}{n} \\ n=10 \end{gathered}\)\(\begin{gathered} \bar{x}=\frac{6+14+7+4+12+8+13+4+18+14}{10} \\ \bar{x}=\frac{100}{10} \\ \bar{x}=10 \end{gathered}\)Hence,
The mean = 10
To calculate the variance, we will use the formula below
\(^{}\sigma^2=\frac{\sum ^{\infty}_{n\mathop=0}(x-\bar{x})^2}{n}\)\(\begin{gathered} \sigma^2=\frac{\sum ^{\infty}_{n\mathop{=}0}(x-\bar{x})^2}{n} \\ (x-\bar{x})^2=(6-10)^2+(14-10)^2+(7-10)^2+(4-10)^2+(12-10)^2+(8-10)^2+(13-10)^2+(4-10)^2+(18-10)^2+(14-10)^2 \\ (x-\bar{x})^2=16+16+9+36+4+4+9+36+64+16 \\ (x-\bar{x})^2=210 \end{gathered}\)\(\begin{gathered} \sigma^2=\frac{\sum ^{\infty}_{n\mathop{=}0}(x-\bar{x})^2}{n} \\ \sigma^2=\frac{210}{10} \\ \sigma^2=\frac{210}{10} \\ \sigma^2=21 \end{gathered}\)Hence
The variance = 21
To calculate the standard deviation,
\(\begin{gathered} \sigma=\sqrt[]{variance} \\ \sigma=\sqrt[]{21} \\ \sigma=4.58 \end{gathered}\)Hence,
The standard deviation is = 4.58

If f1 is 3.8 i 6.3 j and f2 is 9.3 i 3.0 j, what is the magnitude of the projection of f1 onto the line of action of f2?
Answers
The magnitude of the projection of f1 onto the line of action of f2 is 5.55.
The magnitude of the projection of f1 onto the line of action of f2 can be calculated using the dot product of the two vectors. The dot product is given by the formula:
f1 • f2 = |f1| |f2| cos θ
Where f1 • f2 is the dot product of f1 and f2, |f1| and |f2| are the magnitudes of f1 and f2 respectively, and θ is the angle between the two vectors.
To find the magnitude of the projection, we need to find the dot product of f1 and f2 and divide it by the magnitude of f2. The magnitude of the projection is given by:
Magnitude of the projection = (f1 • f2) / |f2|
Let's calculate it step by step:
Step 1: Calculate the dot product of f1 and f2:
f1 • f2 = (3.8 * 9.3) + (6.3 * 3.0) = 35.34 + 18.9 = 54.24
Step 2: Calculate the magnitude of f2:
|f2| = √(9.3^2 + 3.0^2) = √(86.49 + 9) = √95.49 = 9.772
Step 3: Calculate the magnitude of the projection:
Magnitude of the projection = (f1 • f2) / |f2| = 54.24 / 9.772 = 5.55
Therefore, the magnitude of the projection of f1 onto the line of action of f2 is 5.55.
To know more about projection refer here:
https://brainly.com/question/32619127
#SPJ11
HELP!!!
The question is in the image below!!!!

Answers
No, this is not a function because it does not have any equal values.
Based on the graph, how many calories will Colin burn if he walks 3 mi.?
A. 300 calories
B. 550 calories
C. 750 calories
D. 900 calories

Answers
7. The base of a solid is the region bounded by the graphs of y = 3x, y = 6, and x = 0. The cross-sections perpendicular to the x-axis are a. rectangles of height 10. b. rectangles of perimeter 20.
Answers
The cross-sections perpendicular to the x-axis in this particular case are rectangles of height 10. The base of this solid is the region that is bounded by the graphs of y = 3x, y = 6 and x = 0. The graphs of these three lines will form a triangle with base equal to 2, height equal to 6, and area of 6 square units.
The cross-sections perpendicular to the x-axis in this particular case are rectangles of height 10. The base of this solid is the region that is bounded by the graphs of y = 3x, y = 6 and x = 0. The graphs of these three lines will form a triangle with base equal to 2, height equal to 6, and area of 6 square units. The height of the solid in this case will be 10 as that's what the rectangle of height 10 represents. The cross-sections of the solid are perpendicular to the x-axis, which means that they are perpendicular to the base of the solid as well. This means that the cross-sectional area will be the product of the height and the width of the cross-section. The width of the cross-section in this case is equal to 2x, and since the cross-section is a rectangle, the perimeter of the rectangle is equal to 2(width + height) = 2(2x + 10) = 4x + 20. Since the question asks about the cross-sectional perimeter, we can conclude that the answer to the question is b. rectangles of perimeter 20.
To know more about perimeter visit: https://brainly.com/question/7486523
#SPJ11
The volumes of solids in the question can be calculated by using integrals with the base area and the height or width of the rectangular cross-sections. For rectangles of constant height, we find the width from the difference between the two functions and multiply it by the height. For cross-sections of a constant perimeter, the calculation is a bit more complex.
Explanation:The subject of this question is the calculation of the volume of a solid. This solid is defined by the bounded region by the graphs of \(y = 3x, y = 6\), and x = 0, meaning its base is a triangle. The cross-sections perpendicular to the x-axis are rectangles of either height 10 or perimeter 20. To calculate the volume, we need to find the area of each cross-section and integrate over the range from x=0 to where y=6 intersects with y=3x (which is at x=2).
For rectangles with constant height, the width varies thus we use the equations of the boundary lines. The width of the rectangle is the difference between the two functions at a specific x, or 6 - 3x. Multiply this by the height of 10 to get the cross-sectional area. Then, we integrate the area over the x-range of the base, which is [0,2]. As for rectangles of constant perimeter, this requires more steps and could rather be achieved by setting up and solving a system of equations using x and y.
Learn more about Volume of Solids here:https://brainly.com/question/34466655
#SPJ12
y is inversely proportional to the square of x. y=1 when x=10. find y when x=5
Answers
\(\qquad \qquad \textit{inverse proportional variation} \\\\ \textit{\underline{y} varies inversely with \underline{x}} ~\hspace{6em} \stackrel{\textit{constant of variation}}{y=\cfrac{\stackrel{\downarrow }{k}}{x}~\hfill } \\\\ \textit{\underline{x} varies inversely with }\underline{z^5} ~\hspace{5.5em} \stackrel{\textit{constant of variation}}{x=\cfrac{\stackrel{\downarrow }{k}}{z^5}~\hfill } \\\\[-0.35em] ~\dotfill\)
\(\stackrel{\textit{"y" varies inversely with }x^2}{y = \cfrac{k}{x^2}}\hspace{5em}\textit{we also know that} \begin{cases} x=10\\ y=1 \end{cases} \\\\\\ 1=\cfrac{k}{10}\implies 10 = k\hspace{9em}\boxed{y=\cfrac{10}{x^2}} \\\\\\ \textit{when x = 5, what's "y"?}\qquad y=\cfrac{10}{5^2}\implies y=\cfrac{10}{25}\implies y=\cfrac{2}{5}\)
(Grad point )What is m

Answers
Answer:
Either b or c
Step-by-step explanation:
answers and work for them please

Answers
Answer:
no solution
no solution
Step-by-step explanation:
To solve radical equations, you need to isolate the square root and square both sides. Then at the end, you must check solutions for extraneous solutions.
10.
\( \sqrt{5x - 10} + 6 = 4 \)
\( \sqrt{5x - 10} = -2 \)
A square root is always a non-negative number. Since the square root on the left equals -2, there is no real solution.
11.
\( \sqrt{2x^2 + 8x - 4} + 6 = 5 \)
\( \sqrt{2x^2 + 8x - 4} = -1 \)
A square root is always a non-negative number. Since the square root on the left equals -2, there is no real solution.
a random sample of 150 people was taken. 98 of the people in the sample favored candidate a. we are interested in determining whether or not the proportion of the population in favor of candidate a is significantly more than 57%. [r] refer to exhibit 9-6a. at the 0.1 level of significance, what conclusion do you draw? group of answer choices
Answers
At the 0.1 level of significance, the conclusion we come up with is to reject the null hypothesis.
we are given that a random sample of 150 people was taken. 98 of the people in the sample favored the candidate, were it to determine whether or not the proportion of the population in favor of candidate a is significantly more than 57%.So we need to find the test statistic, which is 1.98 determined from the z score, here the rejection region is the number more than 1.28, and 1.98 is greater than 1.28, so it is better to simply reject the null hypothesis.
to know more about the null hypothesis refers to the link https://brainly.com/question/28920252?referrer=searchResults.
#SPJ4
(8p2 −5p4 −2p3)+(4p3 +2p2 −2p4)
Answers
Answer: −
7p^4 + 2p^3 + 10p^2
Step-by-step explanation:
I need help please help me

Answers
Answer:
did you use google.if not use it it is good to use.
Need answers quickly need it step by step
(−5)2 −2×(−9)+6=
(−9)−(−8)+2×42=
8÷(−4)×(−6)2 +7=
10×5−(−6)2 +(−8)=
(10 ÷ (−5) − (−2)) × (−3)3=
3×10+8−42=
(−3)3 −2+8÷(−8)=
4×(−8)+6−(−2)3=
(−5)2 ×3÷5+9=
4 × (−6) ÷ 8 + 33=
Thanks
Answers
Answer:
Step-by-step explanation:
1. -10+18+6=8+6=14
2. -1+84=83
3. -2×(−6)2 +7=12×2+7=24+7=31
4. 50-(−6)2 +(−8)=50+12-8=62-8=54
5. (-2+2)× (−3)3=0× (−3)3=0
6. 30+8-42=38-42=-4
7. -9-2-1=-12
8. -32+6+6=-20
9. -10×3÷5+9=-30÷5+9=-6+9=3
10. -24÷ 8 + 33=-3+33=30