Complete each statement by circling the correct answer based on the figure
below
M
a. One small triangle is what portion of the figure?
1 fourth
1 half
1 third
n
b. One square is what portion of the figure?
1 fourth
1 half
1 whole
ИИ
One rectangle that is not a square is what portion of the figure?
1 half
1 fourth 1 whole

Answers
Answer:
a. 1 fourth
b. 1 half
c. 1 whole
Related Questions
Hree people play a game in which one person loses and two people win each round. The loser must pay each winner the amount that the winner already has. The players agree to play three rounds. At the end of the three rounds, each player has lost one round and has $8. How much money did each player have at the start
Answers
Answer:
$7 ; $4 ; $3
Step-by-step explanation:
Given that:
1 player loses and 2 wins
Loser pays each winner amount each winner already has
3 rounds was played
At the end, each player has lost 1 round each and has $8.00
Since each player lost 1 round each, then each player won twice.
Given that the players are A, B and C
Starting from the last round :
Recall; they all have $8 after the last round.
If A lost the last round and pays B and C the amount they already have.
B and C finally have $8, Hence amount A paid B and C = 8/2 = $4 each
Hence, at the end of 2nd round / before last round :
A has ($8 paid + $8 final) = $16
B and C each have $4
End of first round before 2nd round of game:
If B lost, and pays A and C the amount they already have ;
A finally has 16 hence, amount B pays A = 16/2 = $8
Amount B pays C = 4/2 = $2
A = $8
B = $4 + $(8 + 2) = $14
C = $2
Ist round
C will lose :
Amount C pays B = $14 / 2 = $7
Amount C pays A = $8 /2 = $4
Hence, amount C has before round 1:
$7 + $4 + $2 = $13
Hence; Before the game ;
Either of the three players have ;
$7 ; $4 and $13
Please answer correctly !!!!! Will mark brainliest answer !!!!!!!!!!

Answers
Answer:
same
Step-by-step explanation:
The maximum of f(x) is 8 because it's written in vertex notation. From the graph, g(x)'s maximum is 8 so the answer is that they have the same maximum.
Given and f'(-1)=2 and f(-1) = 2 Find f'(x) = and find f(1) = f"(z) = 5x + 1
Answers
f'(x) = 2x + C (where C is the constant of integration)
f(1) = 2 + C (where C is the constant of integration)
f"(z) = 5
To find the derivative function, f'(x), we need to integrate the given derivative, f'(-1) = 2.
Integrating f'(-1) with respect to x will give us the original function, f(x), up to a constant of integration. Thus, integrating 2 with respect to x gives us 2x + C, where C is the constant of integration.
Hence, f'(x) = 2x + C.
To find f(1), we can substitute x = 1 into the function f(x) = 2x + C. This gives us f(1) = 2(1) + C = 2 + C.
As for f"(z), we can differentiate the given expression for f'(x) = 5x + 1 to find the second derivative. The derivative of 5x + 1 with respect to x is 5.
Therefore, f"(z) = 5.
Know more about derivative here:
https://brainly.com/question/29020856
#SPJ11
Which relationship is described by the equation y=5x
Answers
Answer:
Direct Variation / Proportinal
Step-by-step explanation:
A general form for a direct variation equation is:
\(y=kx\)
'k' is the constant of proportionality.
We can see that the equation given is in that general form, where 5 is the constant or proportionality, or the slope.
Hope this helps.
A shipping crate is packed with unit cubes. The length of the crate is 4
units, the width is 2 units, and the height is 4 units. Find the volume
of the shipping crate.
Answers
Answer:
The volume of shipping crate is 32 unit cubes.
Step-by-step explanation:
Given that:
Length of the crate = 4 units
Width of the crate = 2 units
Height of the crate = 4 units
Volume of shipping crate = Length * Width * Height
Volume of the crate = 4 * 2 * 4
Volume of crate = 32 unit cubes.
Hence,
The volume of shipping crate is 32 unit cubes.
Answer:
32 units
Step-by-step explanation:
#15
Hi there,
I would really appreciate it if someone could help me solve
these . PLEASE SHOW YOUR WORK, so I can understand much
better.
thank you, advance
Find the volume of the figure, where x = 30 cm and h = 27 cm. Give the exact answer and an approximation to the nearest hundredth. cm³ cm3 X Right regular triangular pyramid ≈
Answers
The radius of a circle with an area of 289 cm² can be found by taking the square root of the area divided by π.
The area of a circle is given by the formula A = πr², where A represents the area and r represents the radius of the circle. In this case, the area is given as 289 cm². To find the radius, we rearrange the formula to solve for r.
We start by dividing both sides of the equation by π, which gives us A/π = r². Substituting the given area of 289 cm², we have 289/π = r².
To find the radius, we take the square root of both sides of the equation, which gives us √(289/π) = r.
Calculating the square root of 289 gives us 17, and the square root of π is an irrational number, approximately 1.7725. Thus, the radius of the circle is approximately 17/1.7725 = 9.59 cm.
Therefore, the radius of the circle with an area of 289 cm² is approximately 9.59 cm.
Learn more about square root here:
https://brainly.com/question/29286039
#SPJ11
Find the radius of a circle that has an area of 289 cm². 10 x cm
A farmer set out 600 tomato plants. The numþer
of plants in each row/ was 10 less than twice the
number of rows. How many plants were there in
each row?
Answers
Answer:
Step-by-step explanation:
Let's call the number of rows "x". The number of plants in each row would be 2x - 10. We know that the total number of plants is 600, so we can set up an equation:
x * (2x - 10) = 600
Expanding the left side:
x^2 + 10x - 600 = 0
We can solve for x using the quadratic formula:
x = (-10 ± √(10^2 - 4 * 1 * -600)) / 2 * 1
x = (-10 ± √(100 + 2400)) / 2
x = (-10 ± 50) / 2
x = 20 or -5 (but x cannot be negative, as the number of rows must be a positive integer)
So, there are 20 rows with 10 plants in each row. The number of plants in each row is 2x - 10 = 2 * 20 - 10 = 30.
what is the value of (-5)^4?
Answers
Answer:
625
Step-by-step explanation:
(-5)×(-5)×(-5)×(-5) = 625
Answer:
625
Step-by-step explanation:
-5x-5x-5x-5=625
use a venn diagram to illustrate the relationship a ⊆ b and b ⊆ c.
Answers
Here is a Venn diagram illustrating the relationship between the sets a, b, and c, where a is a subset of b and b is a subset of c:
_______________
| c |
| |
| _________
| | |
| | b |
| | |
| |______ |
| | |
| a |__|
|_______________|
In this diagram, the set c is represented by the outer rectangle, the set b is the area inside the rectangle but outside the inner circle, and the set a is the area inside both the rectangle and the inner circle.
Since a is a subset of b, every element in a is also in b, and therefore the inner circle is entirely contained within the area representing b.
Similarly, since b is a subset of c, every element in b is also in c, and therefore the area representing b is entirely contained within the outer rectangle representing c.
This diagram shows that if a is a subset of b and b is a subset of c, then a is also a subset of c.
To know more about Venn diagram refer here:
https://brainly.com/question/20795347#
#SPJ11
Rohen decided to collect data to determine if the size of a student's home and the student's age are correlated. He determined the data to have a correlation coefficient of 0. 2. What does this r value indicate? No correlation A strong, positive correlation A weak, positive correlation A negative correlation.
Answers
To solve the problem we must know about the correlation coefficients.
What is the correlation coefficient?The correlation coefficient helps us to know how strong is the relation between two variables. Its value is always between +1 to -1, where, the numerical value shows how strong is the relation between them and, the '+' or '-' sign shows whether the relationship is positive or negative.
1 indicates a strong positive relationship.-1 indicates a strong negative relationship.A result of zero indicates no relationship at all, therefore, independent variable.The correlation coefficient 0.2 denotes, "There is a weak positive relationship between the size of a student's home and the student's age".
Given to us
The correlation coefficient for the data is 0.2.As we can see that the value of the correlation coefficient is 0.2, therefore, it is far from1 meaning the relationship is weak, while the '+' symbol denotes that the relationship is positive.
Hence, the correlation coefficient 0.2 denotes, "There is a weak positive relationship between the size of a student's home and the student's age".
Learn more about Correlation Coefficients:
https://brainly.com/question/15353989
What is the total pressure of a mixture of two gases?
The total pressure of a mixture of gases can be defined as the sum of the pressures of each individual gas: Ptotal=P1+P2+… +Pn. + P n . The partial pressure of an individual gas is equal to the total pressure multiplied by the mole fraction of that gas.
Answers
The total pressure of a mixture of two gases is the finalized value of the summation of the total pressure of each of the gases.
The total pressure of a mixture of two gases can be expressed in the form of an equation, as below,
Total Pressure = Pressure of Gas 1 + Pressure of Gas 2
It is noteworthy to be mentioned that the partial pressure of an individual gas is completely in contrast to that of the individual pressure of a gas. It can be expressed in the form of an equation, as below,
Partial Pressure = Total Pressure of Gas x Mole Fraction of Gas
Learn more about the total pressure here:
https://brainly.com/question/24054667
#SPJ4
Ariana has a points card for a movie theater.
She receives 25 rewards points just for signing up.
She earns 8.5 points for each visit to the movie theater.
She needs 76 points for a free movie ticket.
Write and solve an equation which can be used to determine vv, the number of visits Ariana must make to earn a free movie ticket.
Answers
Answer:
6
Step-by-step explanation:
In the first step I simply took 25 away from 76, as she already has 25 tickets meaning she needs 51 more.
than I divided 51 by 8, which would tell us the number of visits she needs to make

Help asap please!!
Find the missing length. The triangles in each pair are similar

Answers
Two triangles are said to be similar if their corresponding angles are congruent and the corresponding sides are in proportion. the missing lengths of HF is 4 and missing length PR =84.
What are Similar Triangles?
Two triangles are said to be similar if their corresponding angles are congruent and the corresponding sides are in proportion .
Triangle QRS is similar to triangle FGH.
Let us find the length of unknown side.
By comparing the sides.
SR/QR=HF/HG
8/14 = x/7
Apply cross multiplication
14x = 56
Divide both sides by 14
x = 56/14
x = 4
HF = 4
8)
By properties of triangle we have
QP/BP=PR/PC
56/24= x/36
Apply cross multiplication
24x = 2016
Divide both sides by 24
x = 2016/24
x = 84
PR = 84
Hence the missing lengths of HF is 4 and missing length PR =84.
To learn more on similar triangles click:
brainly.com/question/25882965
#SPJ1
Help me pls pls PLSS i will mark u as brainest

Answers
Answer:
∠C = 122° and ∠D = 80°
Step-by-step explanation:
This is a cyclic quadrilateral.
Definition: A cyclic quadrilateral is a quadrilateral (a four-sided two-dimensional shape) drawn inside a circle. Every vertex of the quadrilateral must touch the circumference of the circle.
The opposite angles in a cyclic quadrilateral add up to 180°.
Therefore, ∠A + ∠C = 180° and ∠B + ∠D = 180°
To find the value of ∠C:
∠A + ∠C = 180
∠C = 180 - ∠A
∠C = 180 - 58
∠C = 122°
To find the value of ∠D, first find the value of y:
∠B + ∠D = 180
(3y + 4) + (2y + 16) = 180
5y + 20 = 180
5y = 180 - 20 = 160
y = 160 ÷ 5 = 32
Therefore, y = 32
To find ∠D, substitute found value of y into the expression for ∠D:
∠D = 2y + 16
∠D = 2 x 32 + 16
∠D = 80°
f(x) = 14 - 8x
g(x) includes points in the table shown.
Find the difference when the y-intercept of f(x) is subtracted from the y-intercept of g(x).
х
3
Ja
6
9
12
15
HA
12
17
22

Answers
Answer:
go to desmos it a online graphing calculator that helps with the intercepts
Step-by-step explanation:
A manufacturing machine has a 9% defect rate. (in other words, 9% of the items manufactured have a
defect.)
if 4 items are chosen at random, what is the probability that at least one of them will have a defect?
=
plat least one has a defect)
point, if necessary.)
(round your answer to 4 places after the decimal
Answers
The probability that at least one of them will have a defect is 0.3143
What is the probability that at least one of them will have a defect?If, defect items = 9%
Then, non- defect items = 91%
Applying the binomial formula,
Here ,
x denotes the number of successes desired.
n denotes the number of trials.
p denotes the number of successes in a trial.
q denotes the number of failures in a trial.
Substituting, x = 4
n = 4
p = 0.91 and
q = 0.09
The probability that all the chosen items are not defective is:
P(4 not defective) is given by,
As a result, the likelihood that any one of the 4 chosen items will be flawed is determined by subtracting the likelihood that none of the 4 items are flawed from 1.
P(at least one defective) is given by,
P(at least one defective) = 1- P(4 not defective)
= 1 - 0.6857
= 0.3143
To learn more about probability, refer:
brainly.com/question/24756209
#SPJ4
Here is Triangle A. Lin created a scaled copy of Triangle A with an area of 72 square units. C. What is the length of bottom side of the scaled copy?

Answers
Answer:
The length of bottom side of the scaled copy is 12 u
Step-by-step explanation:
To solve this problem we have to know that to calculate the area of a triangle we use the following formula
a = area
b = base
h = height
a = b * h
In the triangle A the base and the height are equal to 3
b = h
Now that we know that b & h we can calculate the base of the scaled copy
72 u² = b * b
72 u² = (b)²
√(72 u²) = b
12 u = b
The length of bottom side of the scaled copy is 12 u
a matrix consisting entirely of zeros is called a
Answers
A matrix consisting entirely of zeros is called a zero matrix, or an all-zero matrix.
It is denoted with the symbol O and can be written in a matrix form, such as O = [0 0 0 0] where the number of columns and rows depends on the size of the matrix. A zero matrix is a matrix which has all its elements equal to zero. It has a number of special properties that make it useful in linear algebra. For instance, the sum of any two zero matrices is a zero matrix, and any scalar multiple of a zero matrix is a zero matrix. Additionally, the product of two zero matrices is a zero matrix, and the product of a zero matrix and an identity matrix is a zero matrix. These properties make it useful in solving systems of linear equations where all the coefficients are zero. Finally, the inverse of a zero matrix does not exist since its determinant is zero.
Learn more about zero matrix here:
https://brainly.com/question/4470545
#SPJ4
what is 2 divided by 7
Answers
Answer:
3.5 stay safe
Step-by-step explanation:
Answer:
2 divided by 7 is 3 with a remainder of 1.
Step-by-step explanation:
2,4,6. 6+1=7 1 times 2 is 2. 2 times 2 is four. 2 times 3 is six. six plus one is seven. When you divide, you are kinda multipling. 2 divided by 7 equals three with a remainder of one. 2 times what is seven or closest to seven? 2 times 3 is six, therefore closest to seven. What's six plus one? seven. one is your remainder.
use the diagram below to solve for x

Answers
Answer:
see the attachment!
#CarryOnLearning

show that the point (7,1) lies on the perpendicular bisector of the line joining (2,4) and (4,6)
Answers
Answer: True
Step-by-step explanation:
Let the point (7, 1) be Point A
Let the perpendicular bisector of the line joining (2,4) and (4,6) be Line PQ; P(2, 4) and Q(4, 6)
If A (7,1) lies on perpendicular bisector of P(2,4) and Q (4, – 6), then AP=AQ
\(\begin{aligned}\therefore \quad A P &=\sqrt{\left(2-7\right)^2+\left(4-1\right)^2}\:\\&=\sqrt{5^2+3^2}\\&=\sqrt{25+9}=\sqrt{34} \\\mathrm{and} \ \ \ A &=\sqrt{\left(4-7\right)^2+\left(6-1\right)^2}\: \\&=\sqrt{3^2+5^2} \\&=\sqrt{9+25}=\sqrt{34}\end{aligned}\)
Therefore, (7, 1) does lie on the perpendicular bisector of the line joining (2,4) and (4,6)
simplify the numerical expression.
12 +6 ÷ 2
Answers
Answer:
12+3
Step-by-step explanation:
12+6÷2
6÷2=3
12+3
pemdas
Answer:
15
Step-by-step explanation:
Start by dividing 6÷2 which is 3
Then add 3 by 12 which gives you 15
The sum of deviations of the individual observations from their sample mean isO sometimes greater than and sometimes less than zero, depending on the observations O always less than zero O always greater than zero O We do not have enough info to answer this questionO always equal to zero
Answers
The sum of deviations of the individual observations from their sample mean is always equal to zero.
The sum of deviations of the individual observations from their sample mean is always equal to zero. This is because the sum of all the deviations is the sum of a positive and a negative value. When we add the negative value to the positive value, the net result is always zero.To illustrate this, let's take an example. Suppose we have a sample of 5 observations: 2, 4, 6, 8, 10. The mean of the sample is 6. The deviations of the individual observations from the sample mean can be calculated as follows:
2-6=-4
4-6=-2
6-6= 0
8-6= 2
10-6=4
When we add the deviations, we get: -4+(-2)+0+2+4=0. The sum of all the deviations is always equal to zero.
Learn more about deviations here:
https://brainly.com/question/20553308
#SPJ4
$ 72 game; 20% discount
Answers
Answer:
14.4
Step-by-step explanation:
20 percent of 72 is 14.4
For the data in the table, tell whether y varies directly with x. If it does, write an equation for the direct variation. x y 3 5.4 7 12.6 12 21.6
Answers
The required expression of the proportionality is given as y = 1.8x.
Given,
The data
x = 3, 7, 12
y = 5.4, 12.6, 21.6
We have to write an equation for the direct variation.
What is proportionality?
The relationship between two or more sets of values—whether they are directly proportional or inversely proportional to one another—is referred to as proportionality.
Here,
If y is proportional to x,
y ∝ x
y = k x
k = y/x
Then,
k = 5.4/3 = 12.6/7 = 21.6/12 = 1.8
So put k in the proportionality equation,
y = 1.8k
Thus, the required expression of the proportionality is given as y = 1.8x.
Learn more about proportionality here;
https://brainly.com/question/29211747
#SPJ1
2t/t-5 + 1/t-3 = 3 Help..
Answers
Step-by-step explanation:
Given equation is 2t/(t-5) + 1/(t-3) = 3
=> [2t(t-3)+1(t-5)]/(t-5)(t-3) = 3
=> (2t²-6t+t-5)/(t²-5t-3t+15) = 3
=> (2t²-5t-5)/(t²-8t+15) = 3
=> 2t²-5t-5 = 3(t²-8t+15)
=> 2t²-5t-5 = 3t²-24t+45
=>3t²-24t+45-2t²+5t+5 = 0
=> t²-19t+50 = 0
The standard form is t²-19t+50 = 0
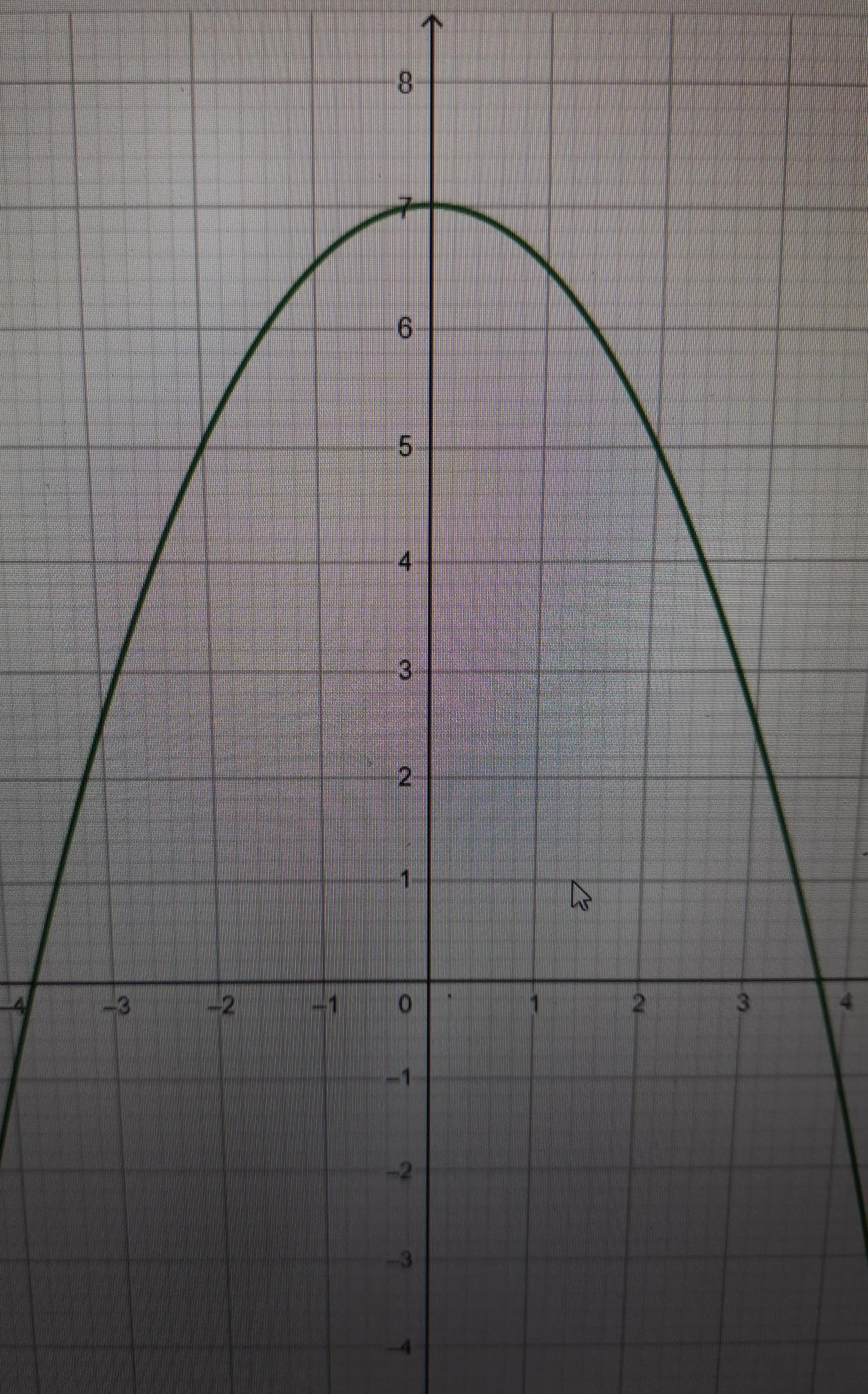
Use the parabola tool to graph the quadratic function
f(x)= -1/2x^2 + 7
Graph the parabola by first plotting its vertex and then plotting a second point on the parabola.

Answers
Answer:
That's the graph for the function f(x)= -1/2 x^2 + 7
The vertex is f(0) = 7
Total pieces of food eaten 57 153 90 food percentage* % % % simulated number of birds in flock for 2nd generation** * divide each flock's total pieces of food by 300, the total number of pieces of food eaten. ** multiply the food percentage for each flock by the total number of birds (30).
Answers
The food percentage would be 19%, 51% and 30%.
Given that we've done it
Number of meals consumed by X = 57
Food consumed by Y = 153.
Number of meals consumed by Z = 90
Total amount of meals consumed = 57 + 153 +90 = 300
Food proportion of flock X thus Equals 57 / 300 * 100 = 19 %
flock food percentage Y =153/300 * 100 = 51 %
flock food percentage Z = 90/300 * 100 = 30 %
This means that the percentages are 19%, 51%, and 30%.
Based on the given information, we have:
Flock X ate 57 pieces of food.
Flock Y ate 153 pieces of food.
Flock Z ate 90 pieces of food.
The total number of pieces of food eaten is 300 (sum of the individual flock's food).
The food percentage for Flock X is 57/300 ≈ 0.19 or 19%.
The food percentage for Flock Y is 153/300 ≈ 0.51 or 51%.
The food percentage for Flock Z is 90/300 = 0.3 or 30%.
The total number of birds for the second generation is 30 (given).
To find the simulated number of birds in each flock for the second generation, we multiply the food percentage for each flock by the total number of birds (30).
For Flock X: 0.19 × 30 = 5.7 (rounded to the nearest whole number: 6 birds)
For Flock Y: 0.51 × 30 = 15.3 (rounded to the nearest whole number: 15 birds)
For Flock Z: 0.3 × 30 = 9 (rounded to the nearest whole number: 9 birds)
Therefore, the simulated number of birds in Flock X, Flock Y, and Flock Z for the second generation are 6, 15, and 9 birds, respectively.
Learn more about whole number here :
brainly.com/question/29766862
#SPJ4
Complete Question
Flock X Flock Y Flock z Total Pieces of Food Eaten 57 153 90 Food Percentage* % 1% % Simulated Number of Birds in Flock for 2nd Generation ** * Divide each flock's total pieces of food by 300, the total number of pieces of food eaten. ** Multiply the food percentage for each flock by the total number of birds (30). DONE
Answer:
19 51 30
6 15 9
second part Is Y then X
Step-by-step explanation:
When the area corresponding to the critical value is in the lower tail of the sampling distribution, the p-value is the area under the curve
a. less than or equal to the critical value.
b. less than or equal to the test statistic.
c. greater than or equal to the critical value.
d. greater than or equal to the test statistic.
Answers
When the area corresponding to the critical value is in the lower tail of the sampling distribution, the p-value is the area under the curve less than or equal to the critical value. Therefore, the correct answer is a. less than or equal to the critical value.
The critical value is the point on the sampling distribution that separates the rejection region from the non-rejection region. If the test statistic falls in the rejection region, we reject the null hypothesis. The p-value is the probability of obtaining a test statistic as extreme or more extreme than the one observed, given that the null hypothesis is true. If the p-value is less than or equal to the critical value, we reject the null hypothesis.
In the case of a lower-tailed test, the critical value is in the lower tail of the sampling distribution, and the p-value is the area under the curve to the left of the test statistic. If the p-value is less than or equal to the critical value, it means that the test statistic falls in the rejection region and we reject the null hypothesis.
Learn more about area
brainly.com/question/27683633
#SPJ11
Simplify (6^4)^3
A. b^9
B. b^3
C. b^12
D. b