Answers
82000 < 460000
Related Questions
need help with What is F(x)=a*b^x please explain the steps

Answers
9514 1404 393
Answer:
33(1,6)2f(x) = 3·2^xStep-by-step explanation:
The blanks you're to fill in explain the steps.
The y-intercept is the value of the function when x=0. It is where the graph crosses the y-axis.
f(0) = a·b^0 = a·1 = a
Reading the y-intercept from the graph, we see ...
The y-intercept is 3. The a-value of the function is 3.
__
The point when x=1 is ...
f(1) = a·b^1 = 3b
Reading the value from the graph, we find the point to be (1, 6). This means ...
3b = 6
b = 2 . . . . . . . divide both sides by 3
The point when x=1 is (1, 6). The b-value of the function is 2.
The equation of the function is f(x) = 3·2^x.
A social psychologist records the age (in years) that a sample of eight participants first
experienced peer pressure. The recorded ages for the participants are 14, 20, 17, 16, 12, 16, 15, and
16. Compute the SS, the variance, and the standard deviation for this sample using the computational formula.
Answers
Using the computational formula for the sample, the SS is 37.50, the variance is 5.36, and the standard deviation is 2.31.
How do we compute the standard deviation using the computational formula?The computational formula is given as follows:
SS = Sum of Squares = ΣX^2 - ((ΣX)^2 / n) ………………………. (1)
X = each value
n = number of values = 8
Therefore, we have:
ΣX^2 = 14^2 + 20^2 + 17^2 + 16^2 + 12^2 + 16^2 + 15^2 + 16^2 = 2,022
(ΣX)^2 = (14 + 20 + 17 + 16 + 12 + 16 + 15 + 16)^2 = 15,876
Substituting all the values into equation (1), we have:
SS = 2,022 - (15,876 / 8) = 37.50
Variance = S^2 = SS / (n – 1) = 37.50 / (8 – 1) = 5.35714285714286, or 5.36
Standard deviation = S = Variance^0.5 = 5.35714285714286^0.5 = 2.31
Learn more about standard deviation here: https://brainly.com/question/12402189.
#SPJ1
a student claimed that the function shown in the table is exponential. do you agree or disagree? explain

Answers
The correct statement that F: "I agree. The ratios of consecutive x-values are constant, and the y-values are increasing at a constant rate."
To determine whether the function shown in the table is exponential, we need to analyze the relationship between the x-values and y-values.
The table shows x-values that are increasing by a power of 2 (1, 2, 4, 8, 16, 32, 64) and y-values that are increasing by a constant rate of 1 (0, 1, 2, 3, 4, 5, 6).
The constant ratio between consecutive x-values indicates exponential growth or decay.
In this case, the function is growing exponentially because the y-values are increasing at a constant rate.
Based on this information, we can conclude that the function is exponential.
Therefore, we agree with statement F: "I agree. The ratios of consecutive x-values are constant, and the y-values are increasing at a constant rate."
The other statements are incorrect because they do not accurately describe the relationship between the x-values and y-values in an exponential function.
Learn more about exponential function here:
brainly.com/question/11487261
#SPJ1

A simple random sample of size nequals15 is drawn from a population that is normally distributed. The sample mean is found to be x overbarequals18.3 and the sample standard deviation is found to be sequals6.3. Determine if the population mean is different from 24 at the alpha equals 0.01 level of significance. Complete parts (a) through (d) below.
(a) Determine the null and alternative hypotheses. Upper H 0: ▼ p sigma mu ▼ less than not equals equals greater than 24 Upper H 1: ▼ sigma mu p ▼ greater than not equals equals less than 24
(b) Calculate the P-value.P-valueequals nothing (Round to three decimal places as needed.)
(c) State the conclusion for the test.
A. Do not reject Upper H 0 because the P-value is less than the alphaequals0.01 level of significance.
B. Do not reject Upper H 0 because the P-value is greater than the alphaequals0.01 level of significance.
C. Reject Upper H 0 because the P-value is less than the alphaequals0.01 level of significance.
D. Reject Upper H 0 because the P-value is greater than the alphaequals0.01 level of significance.
(d) State the conclusion in context of the problem. There ▼ is not is sufficient evidence at the alpha equals 0.01 level of significance to conclude that the population mean is different from 24.
Answers
Answer:
(a) Null Hypothesis, \(H_0\) : \(\mu\) = 24
Alternate Hypothesis, \(H_A\) : \(\mu\neq\) 24
(b) The P-value is 0.004.
(c) Reject Upper H 0 because the P-value is less than the alpha = 0.01 level of significance.
(d) There is sufficient evidence at the alpha equals 0.01 level of significance to conclude that the population mean is different from 24.
Step-by-step explanation:
We are given that a simple random sample of size n = 15 is drawn from a population that is normally distributed. The sample mean is found to be x overbar = 18.3 and the sample standard deviation is found to be s = 6.3.
Let \(\mu\) = population mean
(a) Null Hypothesis, \(H_0\) : \(\mu\) = 24 {means that the population mean is 24}
Alternate Hypothesis, \(H_A\) : \(\mu\neq\) 24 {means that the population mean is different from 24}
The test statistics that will be used here is One-sample t-test statistics because we don't know about population standard deviation;
T.S. = \(\frac{\bar X-\mu}{\frac{s}{\sqrt{n} } }\) ~ \(t_n_-_1\)
where, \(\bar X\) = sample mean = 18.3
s = sample standard deviation = 6.3
n = sample size = 15
So, the test statistics = \(\frac{18.3-24}{\frac{6.3}{\sqrt{15} } }\) ~ \(t_1_4\)
= -3.504
The value of t-test statistics is -3.504.
(b) Now, the P-value of the test statistics is given by;
P-value = P( \(t_1_4\) < -3.504) = 0.002 or 0.2%
For the two-tailed test, the P-value is calculated as = \(2 \times 0.002\) = 0.004 or 0.4%.
(c) Since the p-value of the test statistics is less than the level of significance as 0.002 < 0.01, so we will reject our null hypothesis.
(d) This means that we have sufficient evidence at the alpha equals 0.01 level of significance to conclude that the population mean is different from 24.
(-37)+(-2) please tell quickly
Answers
Answer:-39
Step-by-step explanation:
The first thing is to open the bracket.
By doing that, the question becomes -37-2.
note that plus×minus=minus.
Hence,-39 as the final answer
In the given Fig. PQR is a triangle, right angled at Q. If XY || QR, PQ = 6 cm, PY = 4 cm and PX : XQ = 1 : 2. Calculate the lengths of PR and QR.
Answers
Basic Proportionality Theorem (BPT): If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points then the other two sides are divided in the same ratio. This is also known as Thales theorem.
Given:
\(\angle Q= 90^\circ , XY \ || \ QR, PQ = 6 \ \text{cm}, PY = 4 \ \text{cm} \ \text{and} \ PX : XQ = 1 : 2\)
Since, \(XY \ || \ QR\),
\(PX/XQ = PY/YR\)
[ By Thales theorem (BPT)]
\(\dfrac{1}{2} = PY/YR\) \([PX : XQ = 1 : 2]\)
\(\dfrac{1}{2} = 4 /(PR - PY)\)
\([YR= PR - PY]\)
\(\dfrac{1}{2} = 4 /(PR - 4)\)
\(PR - 4 = 2 \times 4\)
\(PR - 4 = 8\)
\(PR = 8 +4\)
\(PR = 12 \ \text{cm}\)
In right \(\Delta PQR\),
\(PR^2 = PQ^2 + QR^2\)
[ By Pythagoras theorem]
\(12^2 = 6^2 + QR^2\) \([\text{Given} : PQ= 6 \ \text{cm}]\)
\(144 = 36 + QR^2\)
\(144 - 36 + QR^2\)
\(108= QR^2\)
\(QR =\sqrt{108} =\sqrt{3\times36} = 6\sqrt{3} \ \text{cm}\)
Hence, the lengths of PR and QR is 12 cm and \(6\sqrt{3}\) cm.
What is 2(a +8) pls help me I want to pass
Answers
2(a+8)
2xa=2a
2x8=16
Answer=
2a+16
Answer:
2a+16
Step-by-step explanation:
Your first distribute 2(a+8) and get 2a+16.
Whenever a number is in front of a group of numbers in parenthesis, then it is always multiplying. You have to multiply both numbers, and that's how I got 2a+16. Hopefully this helps!
Graph of polygon ABCDE with vertices at negative 1 comma negative 4, negative 1 comma negative 1, 3 comma negative 1, 3 comma negative 4, 1 comma negative 6. A second polygon A prime B prime C prime D prime E prime with vertices at 13 comma negative 4, 13 comma negative 1, 9 comma negative 1, 9 comma negative 4, 11 comma negative 6.
Determine the line of reflection.
Reflection across the x-axis
Reflection across x = 6
Reflection across y = −3
Reflection across the y-axis
Answers
The reflection line that maps polygon ABCDE to polygon A' B' C' D' E' is the y-axis.
What do you mean by reflective line?The image is reflected through a line known as a reflection line. A pattern is said to mirror another pattern, and then every point in the pattern is equidistant from every corresponding point in the other pattern. The reflected image must be the same shape and size, but the image is in the opposite direction.
In order to determine the line of reflection that maps polygon ABCDE to polygon A' B' C' D' E', we must find a symmetrical line equidistant from each corresponding pair of points. If you project the image across the x-axis, vertex A (-1, -4) is mapped to A' (13, -4) and vertex E (1, -6) is mapped to E'. (11, 6). Therefore, the reflection line must be the x-axis.
If we map the image to the cross x=6, vertex A (-1, -4) would correspond to A' (13, -4) and vertex E (1, -6) would correspond to E' (3, 6). ). Therefore, the reflection line cannot be x=6.
If we project the pattern perpendicular to y=-3, the point A (-1, -4) is opposite to the point A' (-7, -4) and the vertex E (1, -6) to the point E . (7, 6). Therefore, the reflection line cannot be y=-3.
If you project the image across the y-axis, point A (-1, -4) is mapped to point A' (-13, -4) and vertex E (1, -6) is mapped to E. (-11 , 6). Therefore, the reflection line must be the y-axis.
Therefore, the reflection line that maps polygon ABCDE to polygon A' B' C' D' E' is the y-axis.
Learn more about Reflection line here
https://brainly.com/question/29248743
#SPJ1
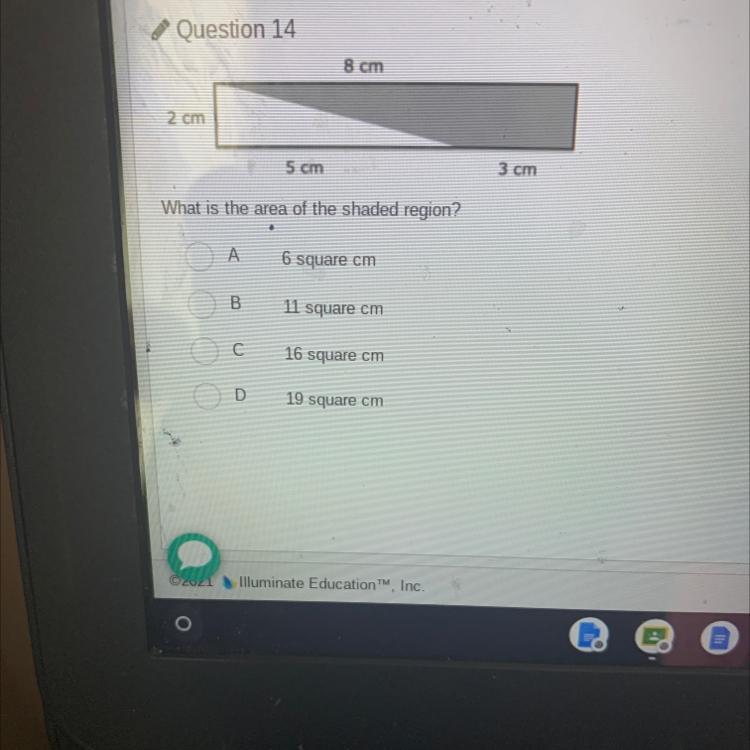
Find the area of each sector. Round your answers to the nearest tenth.

Answers
Answer:
Area of the given sector = 130.9 cm²
Step-by-step explanation:
Area of a sector is given by the formula,
Area of the sector = \(\frac{\theta}{2\pi }\times (\pi r^{2})\)
Area of the sector of the circle given in the picture = \(\frac{\frac{5\pi }{6} }{2\pi }[\pi (10)^{2}]\)
= \(\frac{5}{12}(100\pi )\)
= 130.8996
≈ 130.9 cm²
HELP WITH C
5mph buffer what is the new function and graph?

Answers
The function for fine at every speed should be doubled in construction zones is f(n)= -8.75n+637.5.
What is the function?Functions are the fundamental part of the calculus in mathematics. The functions are the special types of relations. A function in math is visualized as a rule, which gives a unique output for every input x.
The coordinate points from the graph are (10, 550) and (30, 200).
Here, slope = (200-550)(30-10)
= -350/20
= -35/2
= -17.5
Substitute m= -17.5 and (x, y)=(10, 550) in y=mx+c, we get
550=-17.5(10)+c
c=550+175
c=725
So, the equation is y= -17.5x+725
Thus, f(n)= -17.5n+725
a) The fine at every speed should go up by $10.
So, the coordinates are (10, 560) and (30, 210)
New slope (m)= (210-560)(30-10)
= -350/20
= -35/2
= -17.5
Substitute m= -17.5 and (x, y)=(10, 560) in y=mx+c, we get
560=-17.5(10)+c
c=550+175
c=735
So, the equation is y= -17.5x+735
Thus, f(n)= -17.5n+735
b) The fine at every speed should be doubled in construction zones.
So, the coordinates are (20, 550) and (60, 200)
New slope (m)= (200-550)(60-20)
= -350/40
= -8.75
Substitute m= -8.75 and (x, y)=(20, 550) in y=mx+c, we get
550=-8.75(10)+c
c=550+87.5
c=637.5
So, the equation is y= -8.75x+637.5
Thus, f(n)= -8.75n+637.5
Therefore, the function for fine at every speed should be doubled in construction zones is f(n)= -8.75n+637.5.
To learn more about the function visit:
https://brainly.com/question/28303908.
#SPJ1

16 Triangle ABC is translated to triangle A'B'C' by
the following motion rule.
(x, y)(x+2y-5)
-8 -6
G
A. (4,-4)
B. (2,-5)
C. (0.6)
D. (-2.5)
N
8
6
B
-2
S
-6
-8
2
What will be the coordinates of A'?
6 8

Answers
Answer:
To find the coordinates of A' after the translation, we need to apply the motion rule to the coordinates of A:
(x, y) → (x + 2y - 5, y - 6)
Substituting the coordinates of point A, which is (4, -4), into this motion rule, we get:
A' = (4 + 2(-4) - 5, -4 - 6) = (-3, -10)
Therefore, the coordinates of A' after the translation are (-3, -10).
Use cos to solve for a(please no links and show work)

Answers
Who goes to Edgewood Middle School in Ninety Six SC
Answers
Answer:
nope
Step-by-step explanation:
but it's probably better than where i am
i will be doing EASY questions so you guys can get the points
turn 1/2 to a precent
Answers
Answer:
50%
Step-by-step explanation:
if 2/2 is a whole you see its 100% but when its one half its 50%
1/2 can be 5/10 which is 50%
I added a chart for you to look at and remember! <3
—————
Thank you so much! -Doodle
—————

Find the equation of an ellipse satisfying the given conditions. Vertices: (2, -5) and (2,7) Endpoints of minor axis: (-2, 1) and (6, 1)
Answers
Answer:
\(\frac{(x-2)^2}{16}+\frac{(y-1)^2}{36}=1\)
Step-by-step explanation:
Notice how the vertices are on the same x-coordinate and the endpoints of the minor axis are on the same y-coordinate. This indicates that the ellipse is vertical (meaning the ellipse has a vertical major axis of length \(2a\)).
The equation for a vertical ellipse is \(\frac{(x-h)^2}{b^2}+\frac{(y-k)^2}{a^2}=1\) where \((h,k)\) is the center of the ellipse, \((h,k\pm a)\) represents the coordinates of the vertices, and \((h\pm b,k)\) represents the coordinates of the endpoints of the minor axis (also called co-vertices).
The value of \(h\) is listed out for us as \(h=2\).
The value of \(k\) can be determined from taking the midpoint of the vertices. Because \(k=\frac{-5+7}{2}=1\), then \(1-a=-5\) and \(1+a=7\) give us \(a=6\).
Lastly, to figure out \(b\), we solve the equations \(2+b=-2\) and \(2-b=6\) which both give \(b=-4\) as the solution.
Now, plugging in all our values gives us \(\frac{(x-2)^2}{(-4)^2}+\frac{(y-1)^2}{6^2}=1\) which translates to \(\frac{(x-2)^2}{16}+\frac{(y-1)^2}{36}=1\).
Therefore, the final equation of the ellipse that satisfies the given conditions is \(\frac{(x-2)^2}{16}+\frac{(y-1)^2}{36}=1\).
I've attached a graph of the ellipse with labels to help you visualize it.

AA similarity theorem ASA similarity theorem AAS similarity theorem SAS similarity theorem
Answers
Use the histogram to answer the following questions.
Frequency
The frequency of the class 90-93 is
The frequency of the class 94-97 is
This means that a total of
5.5
5
4.5
Your answers should be exact numerical values.
The frequency of the class 86-89 is
86
94
90
Duration of Dormancy (minutes)
dormancy periods were recorded.
Answers
The parameters that are needed to calculate a probability are listed as follows:
Number of desired outcomes in the context of a problem or experiment.Number of total outcomes in the context of a problem or experiment.Then the probability is calculated as the division of the number of desired outcomes by the number of total outcomes, hence it is the same as a relative frequency.
The total number of periods is given as follows:
5 + 6 + 4 = 15.
The frequency of each class is given as follows:
86 - 89: 5/15 = 1/3.90 - 93: 6/15 = 2/5.94 - 97: 4/15.Learn more about the concept of probability at https://brainly.com/question/24756209
#SPJ1

A diagnostic test for a disease is such that it (correctly) detects the disease in 90% of the individuals who actually have the disease. Also, if a person does not have the disease, the test will report that he or she does not have it with probability 0.9. Only 1% of the population has the disease in question. If a person is chosen at random from the population and the diagnostic test indicates that she has the disease, what is the conditional probability that she does, in fact, have the disease
Answers
Answer:
8.33% probability that she does, in fact, have the disease
Step-by-step explanation:
Conditional Probability
We use the conditional probability formula to solve this question. It is
\(P(B|A) = \frac{P(A \cap B)}{P(A)}\)
In which
P(B|A) is the probability of event B happening, given that A happened.
\(P(A \cap B)\) is the probability of both A and B happening.
P(A) is the probability of A happening.
In this question:
Event A: Positive test
Event B: Has the disease
Probability of a positive test:
10% of 100-1 = 99%
90% of 1%
So
\(P(A) = 0.1*0.99 + 0.9*0.01 = 0.108\)
Positive test and having the disease:
90% of 1%
\(P(A \cap B) = 0.9*0.01 = 0.009\)
What is the conditional probability that she does, in fact, have the disease
\(P(B|A) = \frac{P(A \cap B)}{P(A)} = \frac{0.009}{0.108} = 0.0833\)
8.33% probability that she does, in fact, have the disease
List all pairs of alternate exterior,interior,same side interior and corresponding angles.Which pairs above are congruent?

Answers
we have that
alternate exterior angles
< 1 and <5
<2 and <6
alternate interior angles
<3 and <7
<4 and <8
same side interior angles
<3 and <4
<7 and <8
corresponding angles
<1 and <7
<8 and <6
<2 and <4
<3 and <5
Pairs that are congruent------> all pairs are congruent except same side interior angles)
< 1 and <5
<2 and <6
<3 and <7
<4 and <8
<1 and <7
<8 and <6
<2 and <4
<3 and <5
pairs that are supplementary (same side interior angles)
<3 and <4
<7 and <8
9. C(x) = 800 + 20x (a) 10 (b) 50 (c) 200
Answers
Given:
\(c(x)=800+20x\)(a)
Value of function then x is 10.
so:
\(\begin{gathered} c(x)=800+20x \\ x=10 \end{gathered}\)\(\begin{gathered} c(10)=800+20(10) \\ c(10)=800+200 \\ c(10)=1000 \end{gathered}\)(b)
Function at x = 50 then:
\(\begin{gathered} c(x)=800+20x \\ x=50 \\ c(50)=800+20(50) \\ c(50)=800+1000 \\ c(50)=1800 \end{gathered}\)(c)
At x = 200.
\(\begin{gathered} c(x)=800+20x \\ x=200 \\ c(200)=800+20(200) \\ c(200)=800+4000 \\ c(200)=4800 \end{gathered}\)XYZ company is situated in Ghana. They have been commissioned your organisation to design a database for them. The database is expected to keep data on employees, customers, suppliers, and products. Important records on employees such as employee's ID, date of birth, and dependants are expected to be captured in the database. Products information such as product's ID, name of product, manufacturing and expiring data, and name of supplier are expected to be captured. The company receives suppliers from different organisations, hence, it would like the database to capture relevant details of these suppliers. Each supplier supplies only one type of product for the company. Every customer is assigned one sales representative, yet sales representatives maybe assigned up to ten customers. Customers can order an unlimited number of good. Properly represent all entities, relationships, constraints, and appropriate keys in an E-R diagram that can readily be used in a database.
Answers
By answering the presented question, we may conclude that Sales Rep: expression This entity maintains information about sales reps such as SalesRepID and SalesRepName.
what is expression ?An expression in mathematics is a collection of representations, numbers, and conglomerates that mimic a statistical correlation or regularity. A real number, a mutable, or a mix of the two can be used as an expression. Mathematical operators include addition, subtraction, fast spread, division, and exponentiation. Expressions are often used in arithmetic, mathematic, and form. They are used in the representation of mathematical formulas, the solution of equations, and the simplification of mathematical relationships.
The ER diagram above depicts the database entities and their connections. Here's a quick rundown of each entity and its characteristics:
Employee: This object contains information on employees such as EmployeeID, Name, DateOfBirth, and Dependents.
ProductID, ProductName, ManufacturingDate, ExpiryDate, and SupplierID are all stored in this object.
Supplier: This entity holds supplier-specific information such as SupplierID, SupplierName, ContactPerson, and ContactNumber.
CustomerID, CustomerName, ContactPerson, and ContactNumber are all stored in the Customer entity.
Sales Rep: This entity maintains information about sales reps such as SalesRepID and SalesRepName.
To know more about expression visit :-
https://brainly.com/question/14083225
#SPJ1
Correct answer please

Answers
Answer:
50.75
Step-by-step explanation:
We have:
\(E[g(x)] = \int\limits^{\infty}_{-\infty} {g(x)f(x)} \, dx \\\\= \int\limits^{1}_{-\infty} {g(x)(0)} \, dx+\int\limits^{6}_{1} {g(x)\frac{2}{x} } \, dx+\int\limits^{\infty}_{6} {g(x)(0)} \, dx\\\\= \int\limits^{6}_{1} {g(x)\frac{2}{x} } \, dx\\\\=\int\limits^{6}_{1} {(4x+3)\frac{2}{x} } \, dx\\\\=\int\limits^{6}_{1} {(4x)\frac{2}{x} } \, dx + \int\limits^{6}_{1} {(3)\frac{2}{x} } \, dx\\\\=\int\limits^{6}_{1} {8} \, dx + \int\limits^{6}_{1} {\frac{6}{x} } \, dx\\\\\)
\(=8\int\limits^{6}_{1} \, dx + 6\int\limits^{6}_{1} {\frac{1}{x} } \, dx\\\\= 8[x]^{^6}_{_1} + 6 [ln(x)]^{^6}_{_1}\\\\= 8[6-1] + 6[ln(6) - ln(1)]\\\\= 8(5) + 6(ln(6))\\\\= 40 + 10.75\\\\= 50.74\)
(x1,y1) is (-4,-2) and (x2,y2) is (2,4)
Find the equation of the line in slope intercept form
Answers
Answer:
y = x+2
Step-by-step explanation:
(x1,y1) is (-4,-2) and (x2,y2) is (2,4)
Slope intercept form is y = mx+b
m = slope
b = add on
Slope = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Substitute numbers
Slope = \(\frac{4-(-2)}{2-(-4)}\)
Two negatives = one positive
Simplify
\(Slope = \frac{4+2}{2+4}=\frac{6}{6}=1\)
The slope is 1
We can substitute y, x, and the slope
4 = 2*1 + b
4 = 2+b
b = 2
Slope intercept form is y = mx+b
Answer is y = x+2
Hope this helps :)
can someone help me?
(if you can show your work that would be nice).

Answers
Answer:
1. x1=15.75.
2. 24/48=0.5
3. 24/25=0.96
Step-by-step explanation:
1. 15.75/18=0.875
2. you multiply 48 times 0.5 to find 24.
3. multiply 0.96 with 25 to get 24.
Mackenzie has some red, yellow and blue marbles. She has 3200 more red marbles than yellow marbles. She has 3840 more blue than yellow. She gives 1490 blue marbles away. How many more red marbles than blue marbles does she have left?
Answers
Answer:
850
Step-by-step explanation:
Mackenzie has 3200 more red marbles than yellow,
(y + 3200 = r)
And she also has 3840 more blue marbles than the yellow marbles,
(y + 3840 = b)
Then let's assume that Mackenzie has 1 yellow marble.
1 + 3200 = 3201 red marbles
1 +3840 = 3841 blue marbles
If she gives away 1490 blue marbles away, then she is left with 2351 blue marbles.
(3841 - 1490 = 2351)
Now she's left with 2351 blue marbles, and 3201 red marbles.
r - b =?
3201 - 2351 = 850
Mackenzie has 850 more red marbles than blue marbles.
(If you want, you can change the number of yellow marbles, but it will be the same answer.)
What is the y-intercept of the graph shown? Will give the brainiest answer

Answers
Answer:
(0, 4)
Step-by-step explanation:
The y-intercept is defined as the point where the line intersects the y-axis. All we need to do is find where the line intersects the y-axis.
(0, 4) is the answer.
Help PLZZ NO FILES NO FILES
Answers
Answer:
A.) you multiply the 3 and 2
The answer is A lol
2. AB, with A(-3, 4) and B(3,-2), is reflected across the line x=1. Find the coordinates of the
endpoints of the image after this transformation.
Answers
The endpoints of the image of AB after the reflection are A'=(2, -2) and B'=(0, -4).
What are the endpoints?
First, we need to find the equation of the line x=1, which is a vertical line passing through x=1. Since all the points on this line have an x-coordinate of 1, we can say that the equation of this line is x = 1.
Next, we need to reflect the line segment AB across the line x=1. To do this, we can use the following steps:
1. Find the midpoint of the line segment AB.
The midpoint of AB ²can be found by averaging the x-coordinates of A and B, and averaging the y-coordinates of A and B. Therefore, the midpoint is:
(((-3) + 3)/2, (4 + (-2))/2) = (0, 1)
2. Find the equation of the line that passes through the midpoint of AB and is perpendicular to x=1.
Since x=1 is a vertical line, any line perpendicular to it will be a horizontal line. The equation of a horizontal line passing through the point (0,1) is y = 1.
3. Find the intersection point of x=1 and the line found in step 2.
The intersection point of x=1 and y=1 is (1,1).
4. Find the distance between the midpoint of AB and the intersection point found in step 3.
The distance between the midpoint of AB and (1,1) is the same as the distance between the midpoint and the image of the midpoint after reflection across x=1. This distance can be found using the distance formula:
d = √((1 - 0)² + (1 - 1)²) = 1
5. Find the image points of A and B.
The image of A is the same distance from (1,1) as A is from the midpoint of AB. Therefore, the image of A is:
(1 + (1-0), 1 + (1-4)) = (2, -2)
The image of B can be found in the same way:
(1 + (1-3), 1 + (-2-1)) = (0, -4)
Therefore, the endpoints of the image of AB after the reflection are A'=(2, -2) and B'=(0, -4).
To know more about endpoints, visit:
https://brainly.com/question/29164764
#SPJ1
Complete question is: AB, with A(-3, 4) and B(3,-2), is reflected across the line x=1. the coordinates of the endpoints of the image after this transformation are A'=(2, -2) and B'=(0, -4).
Calcular los 3/5 de los 2/3 de las 3/4 de 560
Answers
For the fractions, the calculation of 3/5 of 2/3 of 3/4 of 560 is equal to 168.
How to solve fractions?To calculate 3/5 of 2/3 of 3/4 of 560, break it down step by step:
Step 1: Calculate 3/4 of 560:
3/4 × 560 = (3 × 560) / 4 = 1680 / 4 = 420
Step 2: Calculate 2/3 of the result from Step 1:
2/3 × 420 = (2 × 420) / 3 = 840 / 3 = 280
Step 3: Calculate 3/5 of the result from Step 2:
3/5 × 280 = (3 × 280) / 5 = 840 / 5 = 168
Therefore, 3/5 of 2/3 of 3/4 of 560 is equal to 168.
Find out more on fractions here: https://brainly.com/question/78672
#SPJ1
Scores of students: 30 35 40 45 50 6
No of students: 8 12 15 6 5 4.
find the median scores
and the modal score
Answers
Answer:
Scores of students:
Mean: 34.3
Mode: no mode
No. of students:
Mean: 8.3
Mode: no mode
Step-by-step explanation:
(for scores of students)
6, 30, 35, 40, 45, 50
Mean: 6 + 30 + 35 + 40 + 45 + 50 = 206/6 = 34.3
Mode: there are no mode in the set of data.
(for No. of students)
4, 5, 6, 8, 12, 15
Mean: 4 + 5 + 6 + 8 + 12 + 15 = 50/6 = 8.3
Mode: no mode
