community gym charges a 60$ membership fee and a 70$ monthly fee. workout gym charges a 190$ membership fee and a 60$ monthly fee
Answers
For 13 months the membership is done using the equivalent of two given monthly fees for community and workout gym.
Why do you use the word equivalent?Algebraic equations with equivalent solutions or roots are called equivalent equations. An analogous equation is one that is created by adding or removing the identical quantity or expression from both sides of a given equation. An equation is equivalent if both sides are multiplied or divided by the same non-zero value. By dividing both numbers by the same number, one can convert a division problem into an analogous problem while keeping the ratio between the two numbers constant. The equivalent is defined as something that is almost identical to or equal to another object. Two numbers that are equivalent are (2+2) and 4. These two things are equivalent since 2+2=4. equal to make equivalent.
Let x be the months
then community month= workout month
60+70x=190+60x
⇒70x-60x=190-60
⇒10x=130
⇒x=13 be the months be the working.
To know more about equivalent equations, click here:
https://brainly.com/question/17357101
#SPJ4
Related Questions
Assume you know that a hot-air balloon is currently inflated with a certain amount of air and that the amount is a percent of the total amount required to inflate the balloon. Explain how you would determine the total amount of air required to inflate the balloon.
Answers
Answer:
Percent air is calculated as:
Percent air = Current amount/Total amount *100Solve for total amount of air:
Total amount = Current amount / Percent air * 100Substitute the values in hand to get the answer
what is equivalent to 4 - z - z - z - z
Answers
Answer: 4-4z
Step-by-step explanation: Coming the like terms in order to simplify the equation. There are four z's and they combine as they are like terms. Since we don't know the value of z, thats the most simplified form.
Can you please help me in this question.
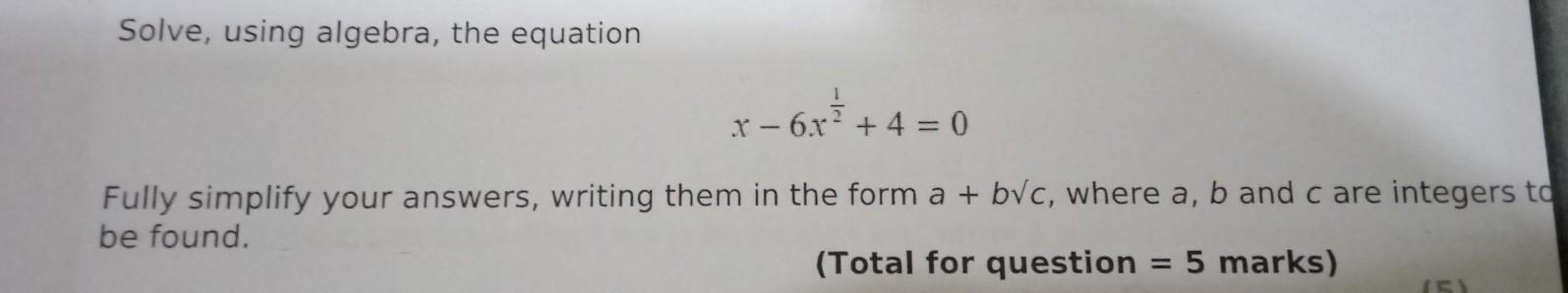
Answers
Answer:
Don't know if i did it right but i think it is:
a=14
b=6
c=5
Suppose that the average cost, in dollars, of producing a shipment of a certain product is C = 5,000x + 20,000/x, x > 0 where x is the number of machines used in the production process. (a) Find the critical values of this function. (Assume 0 < x < [infinity]. Enter your answers as a comma-separated list.) x = Incorrect: Your answer is incorrect. (b) Over what interval does the average cost decrease? (Enter your answer using interval notation.) (c) Over what interval does the average cost increase? (Enter your answer using interval notation.)
Answers
The average cost function is C(x) = 5000x + 20,000/x, where x is the number of machines used in the production. The critical value is C(x) = 20,000 and it happens when x = 2.
If we have a function f(x), the critical point happens when its first derivative is equal to zero.
f '(x) = 0
In the given problem, the function is:
C(x) = 5000x + 20,000/x
Take the derivative:
C '(x) = 5000 - 20,000/x² = 0
5000 x² = 20,000
x² = 4
x = ±2
Since x is within the interval: 0<x<∞, the solution is x = 2
Substitute x = 2 into the function:
C(2) = 5000 (2) + 20000/2
C(2) = 10000 + 10000 = 20,000
Hence, the critical value is C(x) = 20,000 and it happens when x = 2.
Learn more about cost function here:
https://brainly.com/question/2292799
#SPJ4
solution for 3/4x - 12 = -18?
Answers
Answer:
x = -8
Step-by-step explanation:
Add 12 on both sides
You get 3/4x = -6
Multiply 4/3 on both sides
You get x = -24/3
Simplify and you get -8.
Answer:
x=-8
Step-by-step explanation:
The reason why x is -8 is because
The first step is to isolate the x
To isolate the x you got to add 12 to both sides
\(\frac{3}{4}\)x-12+12=-18+12
the -12 gets canceled out by the positive twelve so all thats left now is
\(\frac{3}{4}\)x=-18+12,-18+12 is -6 so its \(\frac{3}{4}\)x=-6
The second step is to divide
now you have to divide by \(\frac{3}{4}\) on both sides
\(\frac{\frac{3}{4} x}{\frac{3}4} } =\frac{-6}{\frac{3}{4} }\)
which \(\frac{3}{4}\) is taken out on the left side because its divided by itself so all thats left is a one,while on the right side -6 divided by three-fourths is -8
PLEASE HELP AND PLEASE MAKE YOUR EXPLANATION DETAILED!!!
Find the direct variation.
if y=28 when x= 168, find y when x =108.
Answers
Answer:
18
Step-by-step explanation:
168 : 28 : : 108 : y
168 / 28 = 108 / y
6 = 108 / y
6 * y = 108
y = 108 / 6
y = 18
Answer:
y = 18
Step-by-step explanation:
Given y varies directly as x then the equation relating them is
y = kx ← k is the constant of variation
To find k use the condition y = 28 when x = 168
28 = 168k ( divide both sides by 168 )
\(\frac{28}{168}\) = k , that is
k = \(\frac{1}{6}\)
y = \(\frac{1}{6}\) x ← equation of variation
When x = 108 , then
y = \(\frac{1}{6}\) × 108 = 18
Which expression or expressions have the same value as 12^2?
Answers
Answer: 6*4 or 8*3
Step-by-step explanation:
12^2=24
12 = 2²*3
you can multiply those factors however you want before raising them to power and you'll always end up with the same result
(2² * 3)² = 12² = 144
(3*2)² * 2² = 6² * 4 = 144
(2²)² * 3² = 16 * 9 = 144
find the volume of a cylinder with a height of 10 and a radius of 2.
125.6in(3) 502.4in(3)
Answers
Answer:
125.6 cubic inches
Step-by-step explanation:
The formula for volume of a cylinder is:
\(V = \pi r^2h\)
---------------------------------------------------------------------------------------------------------------
So:
\(\pi\) × 4 × 10 = 125.6
---------------------------------------------------------------------------------------------------------------
Have a good day :)
A simply supported reinforced concrete beam has a span of 4 m. The beam is subjected to a uniformly distributed dead load (including its own weight) 9.8kN/m and a live load of 3.2kN/m. The beam section is 250mm by 350mm and reinforced with 3-20mm diameter reinforcing bars with a cover of 60mm. The beam is reinforced for tension only with f’c = 27MPa and fy= 375MPa. Determine whether the beam can safely carry the load. Discuss briefly the result.
Answers
The simply supported reinforced concrete beam with the given specifications can safely carry the applied load. The beam section, size, and reinforcement details are sufficient to withstand the imposed loads without exceeding the allowable stress limits.
To determine the beam's safety, we need to calculate the maximum bending moment (M) and the required area of steel reinforcement (As). The maximum bending moment occurs at the center of the span and can be calculated using the formula M = (wL²)/8, where w is the total distributed load and L is the span length.
Substituting the given values, we find
M = (9.8kN/m + 3.2kN/m) × (4m)² / 8
M = 22.4kNm.
To calculate the required area of steel reinforcement, we use the formula As = (M × \(10^6\)) / (0.87 × fy × d), where fy is the yield strength of the steel, d is the effective depth of the beam, and 0.87 is a factor accounting for the partial safety of the material. The effective depth can be calculated as d = h - c - φ/2, where h is the total depth of the beam, c is the cover, and φ is the diameter of the reinforcing bars.
Substituting the given values, we have
d = 350mm - 60mm - 20mm/2
d = 320mm. Plugging these values into the reinforcement formula, we get As = (22.4kNm × \(10^6\)) / (0.87 × 375MPa × 320mm)
As ≈ 0.2357m².
Comparing the required area of steel reinforcement (0.2357m²) to the provided area of steel reinforcement (3 bars with a diameter of 20mm each, which corresponds to an area of 0.0942m²), we can see that the provided reinforcement is greater than the required reinforcement. Therefore, the beam is adequately reinforced and can safely carry the applied loads.
In summary, the given reinforced concrete beam with a span of 4m, subjected to a dead load of 9.8kN/m and a live load of 3.2kN/m, is safely able to carry the applied loads. The beam's section and reinforcement details meet the necessary requirements to withstand the imposed loads without exceeding the allowable stress limits. The calculations indicate that the provided steel reinforcement is greater than the required reinforcement, ensuring the beam's stability and strength.
To learn more about stress refer:
https://brainly.com/question/29488474
#SPJ11
A mountain is in the shape of a cone whose height is about 3.8 kilometers and whose base radius is about 3 kilometers. Approximate the volume of the mountain in cubic kilometers.
The volume of the mountain is approximately cubic kilometers.
(Round to the nearest whole number as needed.)
Answers
Rounding to the nearest whole number, the approximate volume of the mountain is 36 cubic kilometers.
What is volume?Volume is a measure of the amount of space that a three-dimensional object occupies or contains. It is typically measured in cubic units, such as cubic meters, cubic centimeters, or cubic feet.
In the given question,
The volume of a cone can be calculated using the formula V = (1/3)πr²h, where r is the radius of the base, h is the height, and π is approximately 3.14.
Substituting the given values, we get:
V = (1/3) × 3.14 × 3² × 3.8
V ≈ 35.63
Rounding to the nearest whole number, the approximate volume of the mountain is 36 cubic kilometers.
To know more about volume, visit:https://brainly.com/question/30984370
#SPJ1
what is the result of 2.130 x 10³ - 6.6 x 10² =
Answers
Answer:
The answer you're looking for is 1470.
Step-by-step explanation:
The method I used was PEMDAS
Since there was no parenthesis, I simplified the exponents.
2.130 x 10³ - 6.6 x 10² = ?
2.130 x 1000 - 6.6 x 100 = ?
After that, I multiplied all terms next to each other.
2.130 x 1000 - 6.6 x 100 = ?
2130 - 660 = ?
The final step I did was to subtract the two final terms and ended up with 1470 as my final answer.
1470 = ?
I hope this was helpful!
what is the probability of having every bin filled with at least one ball if n balls are distributed randomly in to m bins
Answers
The probability of having every bin filled with at least one ball if n balls are distributed randomly into m bins is given by the formula 1 - (m-1/m)^n.
Let's break it down step-by-step:
Step 1: Probability of a ball being put into a specific Bin Since there are m bins, the probability of a ball being put into a specific bin is 1/m. Therefore, the probability of a ball not being put into that bin is (m-1)/m.
Step 2: Probability of a ball not being put into a specific Bin Since there are m bins, the probability of a ball not being put into a specific bin is (m-1)/m. Therefore, the probability of a ball being put into that bin is 1/m.
Step 3: Probability of every bin being filled with at least one ball Using the above two probabilities, the probability of a specific bin not being filled with a ball is (m-1)/m. Therefore, the probability of all m bins not being filled with a ball is (m-1/m)^n. Finally, the probability of every bin being filled with at least one ball is 1 - (m-1/m)^n.
Therefore, the probability of having every bin filled with at least one ball if n balls are distributed randomly in to m bins is given by the formula 1 - (m-1/m)^n.
To know more about probability, refer here:
https://brainly.com/question/30034780
#SPJ11
Find the slope of each line. Tell whether the slop is Positive, Negative, Undefined or Zero

Answers
Because the line crosses at the y axis and you would have to find another line that’s right on the corner of a square, so you divide 1 and 1 and it’s 1
The expression 0. 15c-0. 072 factored is
Answers
By factoring out this common factor, we obtain the simplified expression 0.006(25c - 12).
We can start by determining the common factor between the two terms in order to factor the phrase 0.15c - 0.072. The common factor in this situation is 0.006, which we may factor out to obtain:
0.15c - 0.072 = 0.006(25c - 12) (25c - 12)
As a result, factoring the expression 0.15c - 0.072 gives 0.006 (25c - 12).
It is possible to utilise this factored form to further simplify calculations or to resolve equations that contain this statement. If we needed to find c in the equation 0.15c - 0.072 = 0, for instance, we could use the factored form to obtain:
0.006(25c - 12) = 0
25c - 12 = 0
c = 12/25
In conclusion, factoring the expression 0.15c - 0.072 involves finding the common factor between the two terms, which is 0.006. By factoring out this common factor, we obtain the simplified expression 0.006(25c - 12).
Learn more about expression here:
https://brainly.com/question/14083225
#SPJ4
please help me with this one

Answers
Answer:
50.24
Step-by-step explanation:
a=(pi)r²
A =(pi)4²
A = 50.27
but I used the actual pi if you use 3.14 I think you'll get 50.24 but that's the closest answer.
Hope you get it right
I really need help with this question please and thank you

Answers
Answer:
8.5
Step-by-step explanation:
this is a right triangle so we could use the formula, which is Pythagorean theorem
so it is \(13.5^{2} -10.5^{2} =72\\\sqrt{72} =8.5\)
If+you+invest+$100+at+an+interest+rate+of+15%,+how+much+will+you+have+at+the+end+of+eight+years?
Answers
Answer:
$305.9022863 or $305.90 (rounded to 2 decimal places)
Step-by-step explanation:
It is a compound interest, meaning an interest accumulates on an initial amount every period. The formula
A= P(1+R)^n
A= the total amount P=Initial amount R= rate n=time period
P=$100 R=15% or 0.15(decimal) n=8 (years)
A= 100 (1.15)^8
A= 100(3.059022863)
A=305.9022863
The amount you will have after 8 years is $220
Calculating simple interestThe formula for calculating simple interest is expressed as:
SI =PRT
P is the principal = $100
T is the time = 8 years
R is the rate. = 15%
SI = 100 * 8 * 0.15
SI = $120
Amount after 8years = $100 + $120
Amount after 8years = $220
Hence the amount you will have after 8 years is $220
Learn more on interest here: https://brainly.com/question/2151013
#SPJ12
76. 6 25. 5 10. 87 =
What wa Sela' etimate and what i the actual um of the number?
Answers
The estimate for the sum of the numbers is 230, and the actual sum of the numbers is 209.
To estimate the sum of the numbers, we can round each number to the nearest ten and then add them together. When rounding off to the nearest tens, we look at the number at the tenth position. If it is five and above, we round it off to the next nearest tens number and if it is below five, we round it off to the previous nearest tens number.
76 rounds to 80 since 6 is above 5
6 rounds to 10 since 6 is above 5
25 rounds to 30 since 5 is located at 5 and above interval
5 rounds to 10 since 5 is located at 5 and above interval
10 rounds to 10 since 0 is below 5
87 rounds to 90 since 7 is above 5
So, the estimate for the sum of the numbers is: 80 + 10 + 30 + 10 + 10 + 90 = 230
To find the actual sum of the numbers, we simply add them together without rounding:
76 + 6 + 25 + 5 + 10 + 87 = 209
The complete question is: 76. 6 25. 5 10. 87 =
What was Sela's estimate and what is the actual sum of the number?
More such examples on estimation of numbers can be found here: https://brainly.com/question/30545404
#SPJ11
a cylinder has a diameter of 10 cm. what might its volume be? give the radius, area of base, and height for 4 possible volumes. give me a step-by-step explanation so I know how to do it.
Answers
Step-by-step explanation: i dont have an explenation but i think its 2
please answer brailyest

Answers
Answer:
The correct answer is the "≥" sign.
Step-by-step explanation:
We know that the team must score at least 8 goals. This means, that they can earn 8 goals or more. The greater than or equal to sign means that the team can win either exactly 8 goals, or more than 8 goals.
Hope this helps! :D
5/8 multiplied by 3/4 + 1/2
Answers
Answer:
31/32 or 0.96875
Step-by-step explanation:
first you muliply 5/8 by 3/4 then the answer add it to 1/2
Write an equation of the line in point-slope form passing through the point and parallel to the given line.3-X + 52(1,-1) y = 2
Answers
Answer:
Explanation:
The slope of the given line is 3/2
A line parallel to this has the same line but different y-intercept.
IIn point-slope form, it is:
\(y-y_1=m(x-x_1)_{}\)Where
\(\begin{gathered} x_1=1 \\ y_1=-1 \\ m=\frac{3}{2} \end{gathered}\)Using these, we have:
\(\begin{gathered} y-(-1)=\frac{3}{2}(x-1) \\ \\ y+1=\frac{3}{2}(x-1) \end{gathered}\)Let f: R→ R' be a ring homomorphism of commutative rings R and R'. Show that if the ideal P is a prime ideal of R' and f−¹(P) ‡ R, then the ideal f−¹(P) is a prime ideal of R. [Note: ƒ−¹(P) = {a ≤ R| ƒ(a) = P}]
Answers
we are given a ring homomorphism f: R → R' between commutative rings R and R'. We need to show that if P is a prime ideal of R' and f^(-1)(P) ≠ R, then the ideal f^(-1)(P) is a prime ideal of R.
To prove this, we first note that f^(-1)(P) is an ideal of R since it is the preimage of an ideal under a ring homomorphism. We need to show two properties of this ideal: (1) it is non-empty, and (2) it is closed under multiplication.
Since f^(-1)(P) ≠ R, there exists an element a in R such that f(a) is not in P. This means that a is in f^(-1)(P), satisfying the non-empty property.
Now, let x and y be elements in R such that their product xy is in f^(-1)(P). We want to show that at least one of x or y is in f^(-1)(P). Since xy is in f^(-1)(P), we have f(xy) = f(x)f(y) in P. Since P is a prime ideal, this implies that either f(x) or f(y) is in P.
Without loss of generality, assume f(x) is in P. Then, x is in f^(-1)(P), satisfying the closure under multiplication property.
Hence, we have shown that f^(-1)(P) is a prime ideal of R, as desired.
Visit here to learn more about element:
brainly.com/question/25916838
#SPJ11
which is perpendicular to the line x-2y=2
Answers
Answer:
y=-2x+5
Step-by-step explanation:
x-2y=2
2y=x-2
y=(x-2)/2
so the slope is 1/2
for lines to be perpendicular m1m2=-1 so the line must have a slope satisfying the condition
(1/2)m=-1
m=-2
the only line with a slope of -2
If is wrong i'm sorry
Need help quick!!!!! Ada and Steve spend a certain amount of money from their accounts each week at a pet shelter.
The table shows the relationship between the amount of money (y) remaining in Ada's account and the number of weeks (x):
Function 1:
Number of Weeks
(x) Amount Remaining (dollars)
(y)
1 40
2 36
3 32
4 28
The equation shows the relationship between the amount of money, y, remaining in Steve's account and the number of weeks, x:
Function 2:
y = −5x + 40
Which statement explains which function shows a greater rate of change? (1 point)
Function 1, because Ada spends $4 each week and Steve spends −$5 each week
Function 1, because Ada spends $12 each week and Steve spends $35 each week
Function 2, because Steve spends $5 each week and Ada spends $4 each week
Function 2, because Steve spends $40 each week and Ada spends $12 each week
Answers
Answer:
Function 2, because Steve spends $5 each week and Ada spends $4 each week
Step-by-step explanation:
Function 1 shows a rate of change of using two points
(x1, y1) = (40,1)
(x2,y2) = (36,2)
m = (y2-y1)/(x2-x1) = (36-40)/(2-1) = -4
The rate of change is decreasing or spending at $4 per week
Function 2 shows an equation y=mx+b; where m is the slope or the rate of change
m=-5
The rate of change is decreasing or spending at $5 per week
Answer: its C
Function 2, because Steve spends $5 each week and Ada spends $4 each week
:
solve for x 1/4(4x-1)=-1/7-5/7
Answers
Answer:
\(x=-\frac{17}{28}\)
Step-by-step explanation:
\(\frac{1}{4}(4x-1)=-\frac{1}{7}-\frac{5}{7}\)
\(x-\frac{1}{4}=-\frac{6}{7}\)
\(x = -\frac{6}{7} + \frac{1}{4}\)
\(x = -\frac{17}{28}\)
plug \(x\) in the equation to make sure of your answer:
\(\frac{1}{4}(4x-1)=-\frac{1}{7}-\frac{5}{7}\\\frac{1}{4}(4(-\frac{17}{28}) -1)=-\frac{1}{7}-\frac{5}{7}\\-\frac{17}{28} -\frac{1}{4}=-\frac{6}{7}\\-\frac{6}{7}=-\frac{6}{7}\)
Applying L'Hospital's rule is not allowed

Answers
Answer:
-1/2
Step-by-step explanation:
lim x-> π/2 cos x /(2x-π) =
lim (x-π/2)->0 sin (π/2 - x) /2(x-π/2) =
lim (x-π/2)->0 - sin (x - π/2)/2(x-π/2) = -1/2
Please could you simplify 9/30 but keep it as a fraction.
Answers
Answer:
3/10
To simplify a fraction, you need to find the GCF (greatest common factor) between both numbers. The GCF between 9 and 30 is 3
9/10 divide by 3/3 is 3/10
Step-by-step explanation:
Hope this helps!! Mark me brainliest!!
Answer:
\(\frac{3}{10}\)
Hope this helps :)
Step-by-step explanation:
To simplify any fraction, you must first find the GCF of the numerator and denominator
9: 1, 3, 9
30: 1, 2, 3, 5, 6, 10, 15, 30
Both of them are divisible by three so we just have to divide the numerator by three and the denominator by three and we'll find our answer:
9/3 = 3
30/3 = 10
The new fraction is:
\(\frac{3}{10}\)
Find the distance between the spheres x2 + y2 + z2 = 4 and x2 + y2 + 22 = 8x + 8y + 8z - 47. X
Answers
The distance between the two spheres is 6 - √5 units.
To find the distance between the spheres x² + y² + z² = 4 and x² + y² + z² = 8x + 8y + 8z - 47, first rewrite the second equation:
x² - 8x + y² - 8y + z² - 8z = -43
Now, complete the squares for x, y, and z terms:
(x - 4)² - 16 + (y - 4)² - 16 + (z - 4)² - 16 = -43
Combine the constants:
(x - 4)² + (y - 4)² + (z - 4)² = 5
Now, we have two spheres with centers (0, 0, 0) and (4, 4, 4) and radii 2 (from √4) and √5 (from √5), respectively. To find the distance between the spheres, subtract their radii from the distance between their centers:
Distance = √[(4 - 0)² + (4 - 0)² + (4 - 0)²] - 2 - √5
Distance = √(64) - 2 - √5
Distance = 8 - 2 - √5
So, the distance between the two spheres is 6 - √5 units.
To learn more about spheres here:
brainly.com/question/22849345#
#SPJ11
5/6 divided by 10/11
Answers
Answer:
11/12
Step-by-step explanation: