Combine the like terms in the expression to create an equivalent expression. p + 0.2p
Answers
Given expression:
\(=\text{ p + 0.2p}\)We can add the two terms since they have a common term p
Hence, the equivalent expression:
\(\begin{gathered} =\text{ (1 + 0.2)p} \\ =\text{ 1.2p} \end{gathered}\)Answer: 1.2p
Related Questions
Senior executives at an oil company are trying to decide whether to drill for oil in a particular field. It costs the company $750,000 to drill. The company estimates that if oil is found the estimated value will be $3,650,000. At present, the company believes that there is a 48% chance that the field actually contains oil. from a decision tree EMV is =$1002000 Consider the previous problem. Before drilling, the company can hire an expert at a cost of $75,000 to perform tests to make a prediction of whether oil is present. Based on a similar test, the probability that the test will predict oil on the field is 0.55. The probability of actually finding oil when oil was predicted is 0.85. The probability of actually finding oil when no oil was predicted is 0.2. What is the EMV if the company hires the expert?
Answers
If the company hires an expert at a cost of $75,000 to perform tests to predict the presence of oil in the field, the Expected Monetary Value (EMV) is $1,002,500.
To calculate the EMV if the company hires the expert, we need to consider the different scenarios and their probabilities.
Scenario 1: The test predicts oil on the field (with a probability of 0.55).
In this case, the probability of actually finding oil is 0.85.
The value if oil is found is $3,650,000.
Scenario 2: The test does not predict oil on the field (with a probability of 0.45).
In this case, the probability of actually finding oil is 0.2.
The value if oil is found is $3,650,000.
Using these probabilities and values, we can calculate the EMV:
EMV = (Probability of Scenario 1 * Value of Scenario 1) + (Probability of Scenario 2 * Value of Scenario 2) - Cost of Expert
EMV = (0.55 * 0.85 * $3,650,000) + (0.45 * 0.2 * $3,650,000) - $75,000
EMV = $1,002,500
Therefore, if the company hires the expert at a cost of $75,000, the EMV is $1,002,500. This indicates that hiring the expert is a favorable decision based on the expected monetary value.
Learn more about expected monetary value here:
https://brainly.com/question/14909520
#SPJ11
drag step's into the order to correctly solve the equation 4×=112

Answers
you divide 112 by 4 to get 28
The base of a triangle is 6 inches more than 3 times the height. If the area of the triangle is 120 square inches.
find the base and height.
Answers
Answer:
2160
Step-by-step explanation:
6X3=18 so 120X18=2160
Consider the function f(x,y)=2x2−4x+y2−2xy subject to the constraints x+y≥1xy≤3x,y≥0 (a) Write down the Kuhn-Tucker conditions for the minimal value of f. (b) Show that the minimal point does not have x=0.
Answers
The minimal point does not have x = 0.
(a) Kuhn-Tucker conditions for the minimal value of fThe Kuhn-Tucker conditions are a set of necessary conditions for a point x* to be a minimum of a constrained optimization problem subject to inequality constraints. These conditions provide a way to find the optimal values of x1, x2, ..., xn that maximize or minimize a function f subject to a set of constraints. Let's first write down the Lagrangian: L(x, y, λ1, λ2, λ3) = f(x, y) - λ1(x+y-1) - λ2(xy-3) - λ3x - λ4y Where λ1, λ2, λ3, and λ4 are the Kuhn-Tucker multipliers associated with the constraints. Taking partial derivatives of L with respect to x, y, λ1, λ2, λ3, and λ4 and setting them equal to 0, we get the following set of equations: 4x - 2y - λ1 - λ2y - λ3 = 0 2y - 2x - λ1 - λ2x - λ4 = 0 x + y - 1 ≤ 0 xy - 3 ≤ 0 λ1 ≥ 0 λ2 ≥ 0 λ3 ≥ 0 λ4 ≥ 0 λ1(x + y - 1) = 0 λ2(xy - 3) = 0 From the complementary slackness condition, λ1(x + y - 1) = 0 and λ2(xy - 3) = 0. This implies that either λ1 = 0 or x + y - 1 = 0, and either λ2 = 0 or xy - 3 = 0. If λ1 > 0 and λ2 > 0, then x + y - 1 = 0 and xy - 3 = 0. If λ1 > 0 and λ2 = 0, then x + y - 1 = 0. If λ1 = 0 and λ2 > 0, then xy - 3 = 0. We now consider each case separately. Case 1: λ1 > 0 and λ2 > 0From λ1(x + y - 1) = 0 and λ2(xy - 3) = 0, we have the following possibilities: x + y - 1 = 0, xy - 3 ≤ 0 (i.e., xy = 3), λ1 > 0, λ2 > 0 x + y - 1 ≤ 0, xy - 3 = 0 (i.e., x = 3/y), λ1 > 0, λ2 > 0 x + y - 1 = 0, xy - 3 = 0 (i.e., x = y = √3), λ1 > 0, λ2 > 0 We can exclude the second case because it violates the constraint x, y ≥ 0. The first and third cases satisfy all the Kuhn-Tucker conditions, and we can check that they correspond to local minima of f subject to the constraints. For the first case, we have x = y = √3/2 and f(x, y) = -1/2. For the third case, we have x = y = √3 and f(x, y) = -2. Case 2: λ1 > 0 and λ2 = 0From λ1(x + y - 1) = 0, we have x + y - 1 = 0 (because λ1 > 0). From the first Kuhn-Tucker condition, we have 4x - 2y - λ1 = λ1y. Since λ1 > 0, we can solve for y to get y = (4x - λ1)/(2 + λ1). Substituting this into the constraint x + y - 1 = 0, we get x + (4x - λ1)/(2 + λ1) - 1 = 0. Solving for x, we get x = (1 + λ1 + √(λ1^2 + 10λ1 + 1))/4. We can check that this satisfies all the Kuhn-Tucker conditions for λ1 > 0, and we can also check that it corresponds to a local minimum of f subject to the constraints. For this value of x, we have y = (4x - λ1)/(2 + λ1), and we can compute f(x, y) = -3/4 + (5λ1^2 + 4λ1 + 1)/(2(2 + λ1)^2). Case 3: λ1 = 0 and λ2 > 0From λ2(xy - 3) = 0, we have xy - 3 = 0 (because λ2 > 0). Substituting this into the constraint x + y - 1 ≥ 0, we get x + (3/x) - 1 ≥ 0. This implies that x^2 + (3 - x) - x ≥ 0, or equivalently, x^2 - x + 3 ≥ 0. The discriminant of this quadratic is negative, so it has no real roots. Therefore, there are no feasible solutions in this case. Case 4: λ1 = 0 and λ2 = 0From λ1(x + y - 1) = 0 and λ2(xy - 3) = 0, we have x + y - 1 ≤ 0 and xy - 3 ≤ 0. This implies that x, y > 0, and we can use the first and second Kuhn-Tucker conditions to get 4x - 2y = 0 2y - 2x = 0 x + y - 1 = 0 xy - 3 = 0 Solving these equations, we get x = y = √3 and f(x, y) = -2. (b) Show that the minimal point does not have x=0.To show that the minimal point does not have x=0, we need to find the optimal value of x that minimizes f subject to the constraints and show that x > 0. From the Kuhn-Tucker conditions, we know that the optimal value of x satisfies one of the following conditions: x = y = √3/2 (λ1 > 0, λ2 > 0) x = √3 (λ1 > 0, λ2 > 0) x = (1 + λ1 + √(λ1^2 + 10λ1 + 1))/4 (λ1 > 0, λ2 = 0) If x = y = √3/2, then x > 0. If x = √3, then x > 0. If x = (1 + λ1 + √(λ1^2 + 10λ1 + 1))/4, then x > 0 because λ1 ≥ 0.
To know more about constraints, visit:
https://brainly.com/question/17156848
#SPJ11
A quarterback throws an incomplete pass. The height of the football at time t is modeled by the equation h(t) = –16t2 + 40t + 7. Rounded to the nearest tenth, the solutions to the equation when h(t) = 0 feet are –0.2 s and 2.7 s. Which solution can be eliminated and why?
Answers
A quarterback throws an incomplete pass. The height of the football at time t is modeled by the equation h(t) = –16t² + 40t + 7. Rounded to the nearest tenth, the solutions to the equation when h(t) = 0 feet are –0.2 s and 2.7 s.
the solution to be eliminated is -0.2s this is because time do not have negative values
What is a quadratic equation?ax² + bx + c = 0 is a quadratic equation, which is a second-order polynomial equation in a single variable. a.
It has at least one solution because it is a second-order polynomial equation, which is guaranteed by the algebraic fundamental theorem. The answer could be real or complex.
Considering the given function, the answer is both real one is negative the other is positive.
The solution in this case represents time, and time of negative value do not apply in real life
Learn more about quadratic equation at:
https://brainly.com/question/1214333
#SPJ1
Se tiene una pirámide regular cuadrangular cuyas caras laterales forman con la base un angulo que mide 53º y el area de la superficie lateral es 60 ¿cuanto mide la altura?
Answers
Answer:
La altura de la pirámide es de 8.14 unidades.
Step-by-step explanation:
Hay una pirámide cuadrangular regular cuyas caras laterales forman un ángulo que mide 53º con la base y el área de la superficie lateral es 60. ¿Qué altura tiene?
Dado que el área de superficie lateral = 60
Tenemos
Área del triángulo equilátero = (√3 / 4) × a²
(√3 / 4) × a² = 60
a² = 60 / (√3 / 4) = 80 · √3
a = √ (80 · √3) = 11.77 unidades
La altura inclinada = Altura de la superficie inclinada = a × sin (60) = 11.77 × sin (60)
La altura inclinada = 11.77 × sin (60) = 10.194 unidades
La altura de la pirámide = Altura inclinada × sin (ángulo de caras laterales con la base)
La altura de la pirámide = 10.194 × sin (53) = 8.14 unidades.
La altura de la pirámide = 8.14 unidades.
The perimeter of a square that has been enlarged by the same number of inches on each side is represented by the expression (X +
6) + (x + 6) + (x + 6) + (x + 6).
Which expression is equivalent to (x + 6) + (x + 6) + (x + 6) + (x + 6)?
A)
4 + (x + 6)
B)
4(x + 6)
c
4x + 6
D)
X - 24
Answers
quiz 10 147 cars were sold during the month of april. 81 had air conditioning and 82 had automatic transmission. 54 had air conditioning only, 55 had automatic transmission only, and 11 had neither of these extras. what is the probability that a randomly selected car had automatic transmission or air conditioning or both?
Answers
The probability that a randomly selected car had automatic transmission or air conditioning or both is 0.92517.
Total number of cars sold, n = 147
Let A denotes the car is air conditioning.
And B denotes the car is automatic message transmission.
A = 81
B = 82
Number of cars that neither of these extras = 11
Only A = 54
Only B = 55
Now,
P(A ∩ B') = A/n
P(A ∩ B') = 81/147
P(A ∩ B') = 0.551
P(A' ∩ B') = 11/147
P(A' ∩ B') = 0.07483
The probability that a randomly selected car had automatic transmission or air conditioning or both is:
P(A ∪ B) = 1 - P(A' ∩ B')
P(A ∪ B) = 1 - 0.07483
P(A ∪ B) = 0.92517
The likelihood that an automobile chosen at random has either an automatic gearbox, air conditioning, or both is 0.92517.
To learn more about probability link is here
brainly.com/question/11034287
#SPJ4
find the average rate of hange for the function f(x)=2 cos(x^2) on the interval [1,3]
Answers
The average rate of change for the function is (2cos(9) - 2cos(1)) / 2.
To find the average rate of change for the function f(x) = 2cos(x^2) on the interval [1, 3], we can use the formula:
Average rate of change = (f(b) - f(a)) / (b - a)
Here, a = 1 and b = 3. First, we need to evaluate f(a) and f(b):
f(1) = 2cos(1^2) = 2cos(1)
f(3) = 2cos(3^2) = 2cos(9)
Now, plug these values into the formula:
Average rate of change = (2cos(9) - 2cos(1)) / (3 - 1)
Average rate of change = (2cos(9) - 2cos(1)) / 2
This is the average rate of change for the function f(x) = 2cos(x^2) on the interval [1, 3].
To learn more about function, refer below:
https://brainly.com/question/12431044
#SPJ11
as part of video game, the point (5,2) is rotated counterclockwise about the origin through an angle of 5 degrees. find the new coordinates of this point
Answers
The new coordinates of the point (5, 2) after rotating counterclockwise about the origin through an angle of 5 degrees are approximately (4.993, 2.048).
To find the new coordinates of the point (5, 2) after rotating counterclockwise about the origin through an angle of 5 degrees, we can use the rotation formula:
x' = x * cos(theta) - y * sin(theta)
y' = x * sin(theta) + y * cos(theta)
Where (x, y) are the original coordinates, (x', y') are the new coordinates after rotation, and theta is the angle of rotation in radians.
Converting the angle of rotation from degrees to radians:
theta = 5 degrees * (pi/180) ≈ 0.08727 radians
Plugging in the values into the rotation formula:
x' = 5 * cos(0.08727) - 2 * sin(0.08727)
y' = 5 * sin(0.08727) + 2 * cos(0.08727)
Evaluating the trigonometric functions and simplifying:
x' ≈ 4.993
y' ≈ 2.048
KLnow more about coordinates here;
https://brainly.com/question/32836021
#SPJ11
If angle 2 is 5x plus 5 degrees and angle 6 is 30 degrees then what is x
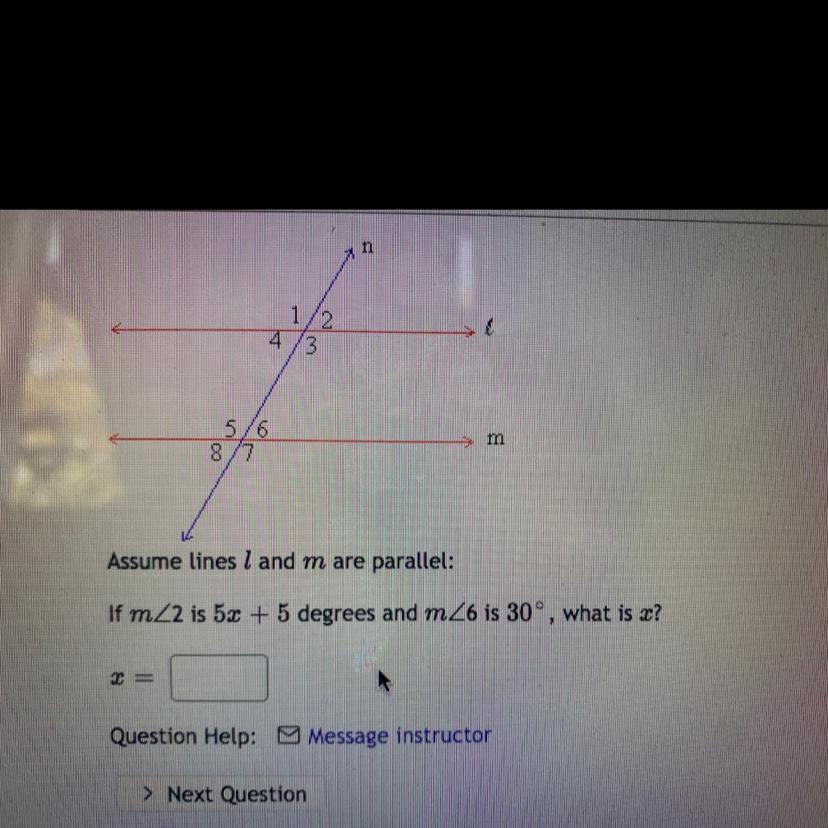
Answers
The value of x is 5.
What is Adjacent angle?Two angles that have the same vertex and a side in common.
Here, m∠2 = m∠6
5x + 5 = 30
5x = 25
x = 25/5
x = 5
Thus, The value of x is 5.
Learn more about Adjacent angle from:
https://brainly.com/question/12838185
#SPJ1
What is the general equation of a tilted ellipses not centered at the origin?
i can't find any information about it for some reason but i need help asap, thank you!
Answers
The general equation of an ellipse in which case it is not centered at the origin and it is tilted is; (x-h)²/a² + (y-k)²/b² = 1.
What is the general equation of a tilted ellipses not centered at the origin?It follows from the task content that the plane shape in discuss is an ellipse which is described by the characteristics that it is tilted and not centered at the origin.
It follows from convention that the general equation of such an ellipse is;
(x-h)²/a² + (y-k)²/b² = 1.
In which case, such an ellipse has center given as point; (h, k).
Read more on ellipse;
https://brainly.com/question/16904744
#SPJ1
I don’t know how to solve these graphs. Can you please help me?

Answers
The equation of the line with slope m and y-intercept b is given by:
\(y=mx+b\)In this case the slope is 5 and the y-intercept is -2; then we have that the equation of the line is:
\(y=5x-2\)Now that we have the equation of the line we can use it to find points on the line, we do that by given values to x (whichever values we want) and use the equation to determine its corresponding y value.
If x=0, then we have:
\(\begin{gathered} y=5(0)-2 \\ y=-2 \end{gathered}\)Hence, the line passes through the point (0,-2).
If x=1, then we have:
\(\begin{gathered} y=5(1)-2 \\ y=5-2 \\ y=3 \end{gathered}\)Hence, the line passes through the point (1,3).
Now that we have two points on the line we graph them on the plane:
Finally, we join the points with a straight line. Therefore, the graph of the line is:


2.39 x 4.37 =
Please solve for me
Answers
Answer:
10.4443
I hope this helps :D have a good day!
Please help explanation if possible

Answers
Answer:
y = 1/7x + 0
Step-by-step explanation:
3x + 21y = 21
21y = -3x + 21
y = -3/21x
y = 1/7x
The chess club decided to raise money with a car wash. They spent $27 on supplies
and charged $5 for each car they washed. Which graph models the chess club's profit
based on the number of cars washed?

Answers
Answer: Thanks!
Step-by-step explanation:
Answer:
Thx!!!
Step-by-step explanation:
I got it right!
What is an equation of the line that passes through the point (6,-2)(6,−2) and is parallel to the line 5x+3y=6
Answers
Answer: y = -(5/3)x + 8
I assume (6,-2)(6,−2) is actually just (6,−2).
Step-by-step explanation:
A parallel line will have the same slope as the reference line. Rewite the reference line equation into y=mx+b format:
5x+3y=6
3y = -5x+6
y = -(5/3)x + 6
The parallel line we want will have the same slope, -(5/3):
y = -(5/3)x + b
b will be different since we want this new, parallel, line to go through point (6,-2), so it must be moved to accomodate this point. Find the value of b we need by entering the point into the new equation and solving for b.
y = -(5/3)x + b for point (6,-2)
-2 = -(5/3)(6) + b
-2 = -10 + b
b = 8
y = -(5/3)x + 8

1/5 divied by 2 as a fraction
Answers
The simplified form of the expression 1/5 divied by 2 as a fraction is 1/10.
What is 1/5 divied by 2 ?Given the expression in the question;
1/5 divied by 2
1/5 ÷ 2
To simplify, multiply 1/2 by the reciprocal of 2
1/5 ÷ 2
1/5 × 1/2
Simplify
( 1 × 1 ) / ( 5 × 2 )
( 1 ) / ( 5 × 2 )
Multiply 5 and 2
( 1 ) / ( 10 )
1/10
Therefore, the simplified form is 1/10.
Learn more about fractions heres; https://brainly.com/question/10354322
#SPJ1
In a recent study, volunteers who had 8 hours of sleep were three times more likely to answer questions correctly on a math test than were sleep-deprived participants.
Answers
Answer:
Step-by-step explanation:
Sleep Deprivation
In a recent study, volunteers who had 8 hours of sleep were three times more likely to answer correctly on a math test than were sleep-deprived participants.
(a) Identify the sample used in the study.
(b) What is the sample's population?
(c) Which part of the study represents the descriptive branch of statitics?
(d) Make an inference based on the results of the study?
Solution
A. The samples used is the hours of sleep and math test scores of the volunteers
B. The samples population is hours of sleep and math test scores of people in general
C. The part of the study that represent the descriptive branch of statistics is "three times more likely"
D.Inference: To perform well in a math test, a person should get at least 8 hours of sleep the night before.
find the value of y if ac = 3y + 5, cb = 4y -1, ab = 9y - 12, and point c lies between a and b
Answers
Given that point c lies between a and b, the numerical value of y is 8.
What is the numerical value of y?Given the data in the question;
Point c lies between a and bSegment ab = 9y - 12Segment ac = 3y + 5Segment cb = 4y - 1Value of y = ?Since point c lines between point a and b on segment ab, segment ab is the addition of segment ac and cb.
Hence,
ab = ac + cb
9y - 12 = (3y + 5) + (4y - 1)
Solve for y by collecting like terms and simplify.
9y - 12 = 3y + 5 + 4y - 1
9y - 12 = 3y + 4y - 1 + 5
9y - 12 = 7y + 4
9y - 7y = 4 + 12
9y - 7y = 4 + 12
2y = 16
y = 16/2
y = 8
Given that point c lies between a and b, the numerical value of y is 8.
Learn more about equations here: brainly.com/question/14686792
#SPJ1
Which values represent the independent variable? (–2, 4), (3, –2), (1, 0), (5, 5) A. {–2, 3, 1, 5} B. {4, –2, 0, 5} C. {–2, 4, 3, –2} D. {–2, –1, 0, 5} Please select the best answer from the choices provided A B C D
Answers
Answer:
The independent variable is the variable that is manipulated or changed during an experiment. In this case, the independent variable is represented by the x-values of the given points.
So, the answer would be option A: {-2, 3, 1, 5}
Step-by-step explanation:
brainliest Plsssss
can you apply the properties of rational exponents to an example?
Answers
We can simplify \((16x^4)^(-1/2) to 1/(4x^2)\) using the properties of rational exponents.
Certainly! Here's an example:
Simplify the expression: \((16x^4)^(-1/2)\)
We can apply the property of rational exponents which states that \((a^m)^n = a^(m*n)\). Using this property, we get:
\((16x^4)^(-1/2) = 16^(-1/2) * (x^4)^(-1/2)\)
Next, we can simplify \(16^(-1/2)\) using the rule that \(a^(-n) = 1/a^n\):
\(16^(-1/2) = 1/16^(1/2) = 1/4\)
Similarly, we can simplify \((x^4)^(-1/2)\) using the rule that \((a^m)^n = a^(m*n)\):
\((x^4)^(-1/2) = x^(4*(-1/2)) = x^(-2)\)
Substituting these simplifications back into the original expression, we get:
\((16x^4)^(-1/2) = 1/4 * x^(-2) = 1/(4x^2)\)
Therefore, the simplified expression is \(1/(4x^2).\)
Learn more on rational exponents here
brainly.com/question/20726608
#SPJ1
please view the image and answer the questions.
This is College Algebra.

Answers
Step-by-step explanation:
x² - 9
1. There is no common factor other than 1.
2. √x² = x; √9 = 3
3. a = x; b = 3
4. x² - 9 = (x - 3)(x + 3)
Alyssa sold half of her comic books and then bought 8 more. She now has
12. How many did she begin with ?
Answers
Answer:
8 Books
Step-by-step explanation:
First find how many she had before buying 8 more-
12 - 8 = 4
Then multiply that by 2
4 x 2 = 8
The had 8 books to begin with
The circumference of a circle is 70 ft. What is the area, in square feet? Express your
answer in terms of 7r.
PLEASE HELP FASSTT

Answers
Answer:
78.54 feet squared
Step-by-step explanation:
Answer:
so formula of finding radius is circumfrence / 2r
so radius = 14
if radius is 14 then area is 615
Step-by-step explanation:
A bag of coins contains only quarters and dimes. The number of dimes in the bag can be represented by x. The number of quarters is 6 more than twice the number of dimes. There are a total of 276 coins in the bag. What is x, the number of dimes in the bag?
Answers
Answer:
There are 90 coins in the bag.
Step-by-step explanation:
Let \(x\), \(y\) the number of dimes and quarters. Now we proceed to translate each relevant sentence into mathematical expressions:
(i) The number of quarters is 6 more than twice the number of dimes:
\(y = 2\cdot x + 6\) (1)
(ii) There are a total of 276 coins in the bag:
\(x + y = 276\) (2)
By applying (1) in (2), we find that the number of dimes is:
\(x+2\cdot x + 6 = 276\)
\(3\cdot x = 270\)
\(x = 90\)
There are 90 coins in the bag.
A car show is making a model of 1980 Ford truck. The model is 10 inches long. If the model truck has a scale of 3 in: 2ft, how tall is the actual truck?
Answers
Answer:
Step-by-step explanation:
3 inches is 2 feet
10 inches is 6.66 feet (no this isn't a joke)
What is the slope of the line with equation y-3- - } (x-2)?
-2
Answers
We can rewrite the linear equation as:
y = -x + 3
There we can see that the slope is -1.
What is the slope of the linear equation?A linear equation written in the slope-intercept form is:
y = a*x + b
Where a is the slope.
Here the linear equation is written kinda weird, I guess that the line is:
y - 3 = -(x - 2) - 2
Let's isolate y and simpify the equation, we will get:
y - 3 = -(x - 2) - 2
y = -(x - 2) - 2 + 3
y = -(x - 2) + 1
Now we can apply the rule of signs in the right side:
y = -x + 2 + 1
y = -x + 3
y = -1*x + 3
So the slope of the linear equation is -1.
Learn more about linear equations:
https://brainly.com/question/1884491
#SPJ1
I need help on how to find a surface area! I will send the full photo!

Answers
we are asked to determine the surface area of the figure. To do that we need to find the areas of each face and add them together. The front face is a trapezoid, and its area is:
\(A_{tz}=\frac{b+B}{2}h\)Where "b" is the upper base, "B" is the lower base and "h" is the height. Replacing the values:
\(A_{tz}=\frac{9ft+4ft}{2}\times4.3ft\)Solving the operations:
\(A_{tz}=28ft^2\)the upper face is a rectangle, its area is the product of its side:
\(A_{uf}=(10ft)(9ft)=90ft^2\)The area of the lower face is also a rectangle, therefore its area is:
\(A_{lf}=(4ft)(10ft)=40ft^2\)The side face is also a rectangle, and its area is:
\(A_{sf}=(5ft)(10ft)=50ft^2\)Now we add the areas having into account that the front and side faces repeat themselves. the total surface area is:
\(A=2A_{tz}+A_{uf}+A_{lf}+2A_{sf}\)replacing the values:
\(A=2(28ft^2)+(90ft^2)+(40ft^2)+2(50ft^2)\)Solving the operations:
\(A=286ft^2\)Therefore, the surface area is 286 square feet.
Am I doing this right?
I have a quiz tomorrow and this is the only thing I don’t get bc fractions confuse me :(
