choose the best decimal equivalent to 14/25.
Answers
Answer:
0.56
Step-by-step explanation:
To find the decimal equivalent, we can divide the numerator and denominator together.
14 ÷ 25 = 0.56
Best of Luck!
Related Questions
what is the solution to the equation 30.16 = 17.56 + 5x
Answers
Answer:
x=1.2
Step-by-step explanation:
First, you have to subtract 17.56 from both sides
then you get 12.6=5x
then you have to divide both sides by five
if you do that you get x=1.2
Answer:
2.52
Step-by-step explanation:
John is saving to buy a new car that will cost him $24,000. John started his savings at the beginning of the school year and has been able to accumulate $1000 after the first month. John plans to continue his savings at a rate proportional to the amount he still needs to save. Determine John's savings amount as function of time Hint: A variable y is said to be proportional to a variable x if y=cx for some constant c.
Answers
John's savings amount as a function of time is S(t) = $24,000 / 25. Initially, he needs to save $24,000 for a new car. After the first month, he has saved $1,000. The savings amount is directly proportional to the time elapsed. The constant of proportionality is 1/24. Thus, John's savings amount can be determined based on the remaining amount he needs to save.
John's savings amount can be represented as a function of time and is proportional to the amount he still needs to save. Let's denote the amount John needs to save as N(t) at time t, and his savings amount as S(t) at time t. Initially, John needs to save $24,000, so we have N(0) = $24,000.
We know that John has saved $1,000 after the first month, which means S(1) = $1,000. Since his savings amount is proportional to the amount he still needs to save, we can write the proportionality as:
S(t) = k * N(t)
where k is a constant of proportionality.
We need to find the value of k to determine John's savings amount at any given time.
Using the initial values, we can substitute t = 0 and t = 1 into the equation above:
S(0) = k * N(0) => $1,000 = k * $24,000 => k = 1/24
Now we have the value of k, and we can write John's savings amount as a function of time:
S(t) = (1/24) * N(t)
Since John's savings amount is proportional to the amount he still needs to save, we can express the amount he still needs to save at time t as:
N(t) = $24,000 - S(t)
Substituting the expression for N(t) into the equation for S(t), we get:
S(t) = (1/24) * ($24,000 - S(t))
Simplifying the equation, we have:
24S(t) = $24,000 - S(t)
25S(t) = $24,000
S(t) = $24,000 / 25
Therefore, John's savings amount at any given time t is S(t) = $24,000 / 25.
To know more about proportional savings, refer here:
https://brainly.com/question/29251832#
#SPJ11
Use the picture of the circle below to find the area of the circle. Use 3.14 for π and show your work.
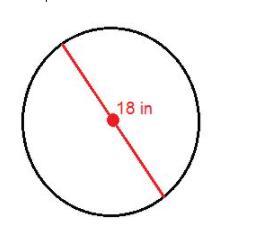
Answers
Answer:
254.34 in^2
Step-by-step explanation:
To calculate the Area of Circle is πr^2
r is the radius of the circle
In this problem, the diameter is given which is 18 in. To find the radius you have to divide the diameter by 2.
18/2 = 9 in is our radius
Area of Circle = π9^2
= 3.14*81
= 254.34 in^2
If f and g are differentiable functions for all real values of x such that f(2) = 5, g(2) = 3, f '(2) = 1, g '(2) = -2, then find h '(2) if h(x) = f(x) g(x).
Answers
Answer:
\(h'(2)=-7\)
Step-by-step explanation:
So we have:
\(h(x)=f(x)g(x)\)
Differentiate. Use the product rule:
\(h'(x)=f'(x)g(x)+f(x)g'(x)\)
Substitute 2 for x:
\(h'(2)=f'(2)g(2)+f(2)g'(2)\)
We know that f'(2) is 1, f(2) is 5, g(2) is 3, and g'(2) is -2. Make the appropriate substitutions:
\(h'(2)=(1)(3)+(5)(-2)\)
Simplify:
\(h'(2)=3-10\)
Subtract:
\(h'(2)=-7\)
15. Describe the three general steps
for producing a recombinant DNA (rDNA) vector, state how rDNA can
be introduced into cells, and discuss the clinical applications of
rDNA.
Answers
Producing rDNA involves isolating and cleaving DNA, inserting fragments into a vector, and transforming host cells. rDNA can be introduced via transformation, transfection, or viral vectors. Clinical applications include protein production, gene therapy, vaccines, and diagnostics.
Producing a recombinant DNA (rDNA) vector involves several general steps. Here are the three main steps involved in the process:
Isolation and Cleavage of DNA:
The first step is to isolate the desired DNA fragments from the source organism. This can be done using various techniques such as PCR (Polymerase Chain Reaction) or restriction enzyme digestion. Restriction enzymes are enzymes that cut DNA at specific recognition sites. By using the appropriate restriction enzymes, the desired DNA fragment and a vector DNA can be cut at specific sites. The vector is usually a plasmid, which is a small circular DNA molecule.
Insertion of DNA Fragments into the Vector:
Once the DNA fragments and vector have been cut, they are mixed together and joined through a process called ligation. DNA ligase is used to catalyze the formation of covalent bonds between the ends of the DNA fragments and the vector. This creates a recombinant DNA molecule containing the desired DNA fragment within the vector. The recombinant DNA molecule is then introduced into host cells for replication.
Transformation of Host Cells:
The recombinant DNA molecules need to be introduced into host cells to produce multiple copies of the recombinant DNA. This is typically done using a process called transformation. Host cells, such as bacteria or yeast, are treated in a way that makes them more receptive to taking up the recombinant DNA. Methods for transformation include heat shock, electroporation, or using chemical agents. Once the host cells have taken up the recombinant DNA, they can be grown in culture to produce large quantities of the desired DNA fragment.
Introduction of rDNA into Cells:
Recombinant DNA can be introduced into cells using various methods, depending on the type of cells being targeted. Some common techniques include:
Transformation: As mentioned earlier, host cells, such as bacteria or yeast, can be treated to make them receptive to taking up the recombinant DNA. This can be achieved by exposing the cells to heat shock, electroporation, or using chemical agents.
Transfection: This method is used for introducing rDNA into eukaryotic cells, including animal cells. It involves the use of techniques such as calcium phosphate precipitation, liposome-mediated transfection, or electroporation.
Viral Vectors: Certain viruses, such as retroviruses, adenoviruses, or lentiviruses, can be modified to carry the recombinant DNA. These viral vectors can then infect target cells and deliver the rDNA into the host genome.
Clinical Applications of rDNA:
Recombinant DNA technology has revolutionized biomedical research and has led to numerous clinical applications. Some important applications include:
Production of Therapeutic Proteins: rDNA technology allows for the production of large quantities of therapeutic proteins, such as insulin, growth factors, clotting factors, and monoclonal antibodies. These proteins can be used to treat various diseases, including diabetes, cancer, and genetic disorders.
Gene Therapy: rDNA vectors can be used to deliver functional copies of genes into target cells to correct genetic defects. This holds promise for the treatment of inherited diseases caused by single gene mutations, such as cystic fibrosis and muscular dystrophy.
Vaccine Development: Recombinant DNA technology has been instrumental in the development of vaccines. By expressing specific antigens from pathogens, recombinant vaccines can be created to stimulate an immune response without causing disease.
Diagnostic Tools: Recombinant DNA techniques are used to produce specific DNA or RNA probes for diagnostic purposes. These probes can detect the presence of specific genes or mutations associated with diseases, aiding in early detection and personalized medicine.
for such more question on isolating
https://brainly.com/question/27746495
#SPJ8
x
This graph shows the amount of charge left on my
computer, c, after I have been awake for h hours.
How many hours will I have been awake when my
computer has no charge left?
Use the sketch tool if it helps you with your thinking.
Submit and Explain

Answers
Answer: It's 4.5 hope it's right, bye
Answer:
Step-by-step explanation:
According to the College Board website, the scores on the math part of the SAT (SAT-M) in a recent year had a mean of 507 and standard deviation of 111. Assume that SAT-M scores follow a normal distribution. One of the criteria for admission to a certain engineering school is an SAT-M score in the 98th percentile. This means the score is in the top 2% of scores.
How does this translate to an actual SAT-M score? Show your work. Note: you may need to find the z-score for the the 98th percentile (or, equivalently, the top 2%). To do this, use the Inverse Normal Distribution Calculator (at the top of this page).
Answers
An SAT-M score in the 98th percentile is approximately 734.55 or higher.
According to the College Board website,
The scores on the math part of the SAT (SAT-M) in a recent year had a mean of 507 and a standard deviation of 111. Assume that SAT-M scores follow a normal distribution. To gain admission to a particular engineering school, a requirement is to obtain an SAT-M score in the 98th percentile, indicating that the score is among the top 2% of scores.
For getting the actual SAT-M score, we need to find the corresponding z-score for the 98th percentile.
Using the Inverse Normal Distribution Calculator, we get a z-score of 2.05 for the 98th percentile.
So, the formula for finding an actual SAT-M score is:
x = μ + zσ
Where x is the actual SAT-M score,
μ is the mean = 507,
z is the z-score = 2.05,
σ is the standard deviation = 111
x = 507 + (2.05)(111)
x = 507 + 227.55
x = 734.55
The actual SAT-M score for the 98th percentile is approximately 734.55 (rounded to the nearest hundredth).
Therefore, an SAT-M score of 734.55 or higher is required for admission to the engineering school.
To know more about the "z-score ": https://brainly.com/question/25638875
#SPJ11
Find the magnitude of
the vector <5, - 3>.
A. 6.1
B. 5.2
C. 4
D. 5.8
Answers
Answer:
5.8
Step-by-step explanation:
\( \sqrt{ {5}^{2} } + \sqrt( { - 3}^{2} )\)
\( \sqrt{25 + 9} \)
\( \sqrt{34} \)
5?8
Find asked slope
(See image for problem)

Answers
Answer:
D has the positive slope because it's the only line that goes upwards from left to right.
Step-by-step explanation:
An advertisement indicated that a new computer priced at $600.00 could be purchased by putting $102.00
down. What percent of the price is the down payment?
Answers
Answer:
17%
Step-by-step explanation:
brainliest pls
can someone please answer this math question

Answers
Answer:
The answer is in the picture
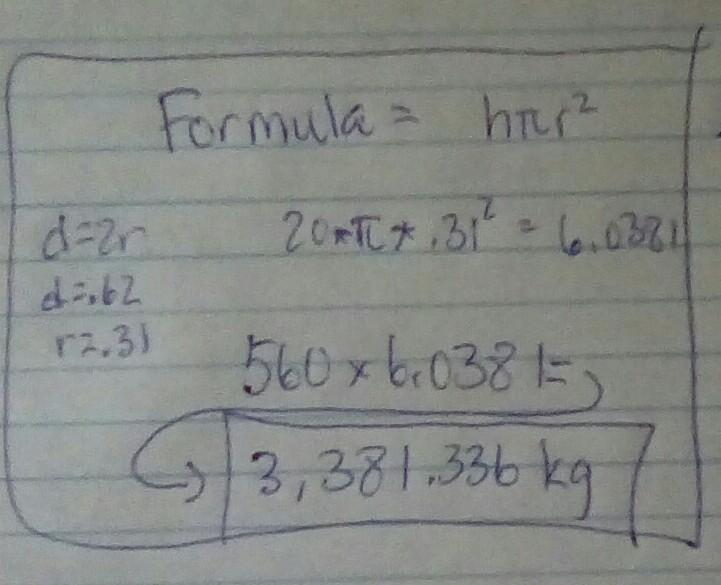
What is the approximate area

Answers
Answer:
2827.43in²
Step-by-step explanation:
formula for area of a circle is r²π with r being the radius (30 in this case)
we can plug in 30 for r to solve for the area
30²π
900π
2827.43
that is the answer
- kan academy advance
6 1/2+2/3+3/4 calcution with distribution
Answers
By the distribution property 6(1/2 + 2/3+3/4) = 23/2
Distribution Property:According to the distributive property, multiplying the difference or aum of numbers will be equivalent to multiplying the individual parts of the difference or sum.
The expression that can explain the above rule is A ( B+ C) = AB + AC
Here we have
6(1/2 + 2/3+3/4)
By distribution property
=> 6(1/2 + 2/3+3/4)
= 6(1/2) + 6(2/3)+ 6(3/4)
= 3 + 2(2) + 3(3/2)
= 3 + 4 + 9/2
= 7 + 9/2
= (14+9)/2 [ add 7 and 9/2 by taking 2 as LCM ]
= 23/2
Therefore,
By the distribution property 6(1/2 + 2/3+3/4) = 23/2
Learn more about Distribution Property at
https://brainly.com/question/6276874
#SPJ1
Complete Question:
1. Find the value of this fraction computation: 6(1/2 + 2/3+3/4)
A car owner pays for new brakes that cost $756.25, with a credit card that has an annual rate of 24.5%. Determine the total amount paid, if the car owner pays $100 a month, until the balance is paid off. A spreadsheet was used to calculate the correct answer. Your answer may vary slightly depending on the technology used. $830.52 $73.76 $892.64 $185.28
Answers
The total amount paid for a credit card purchase of $756.25 at an annual rate of 24.5% and monthly repayment of $100, until the balance is paid off, is $829.79.
How is the total amount determined?The total amount paid by the car owner can be determined using an online finance calculator, setting the following parameters.
The total amount paid includes the principal and the interest for the credit.
The payment period will last for 8 months and some days.
I/Y (Interest per year) = 24.5%
PV (Present Value) = $756.25
PMT (Periodic Payment) $-100
Results:
N = 8.298
Sum of all periodic payments = $829.79
Total Interest = $73.54
Learn more about credit card payments at https://brainly.com/question/2808739
#SPJ1
Two cars travel at the same speed to different destinations. Car A reaches its destination in 12 minutes. Car B reaches its destination in 18 minutes. Car B travels 4 miles farther than Car A. How fast do the cars travel? Write your answer as a fraction in simplest form.
Answers
Answer:
chatGPT
Step-by-step explanation:
Let's denote the speed of each car as v, and the distance that Car A travels as d. Then we can set up two equations based on the information given:
d = v * (12/60) (since Car A reaches its destination in 12 minutes)
d + 4 = v * (18/60) (since Car B travels 4 miles farther than Car A and reaches its destination in 18 minutes)
Simplifying the equations by multiplying both sides by 60 (to convert the minutes to hours) and canceling out v, we get:
12v = 60d
18v = 60d + 240
Subtracting the first equation from the second, we get:
6v = 240
Therefore:
v = 240/6 = 40
So the cars travel at a speed of 40 miles per hour.
\(\left \{ {{x=3} \atop {y+1=0}} \right.\) solve graphically this linear system of equations
Answers
Answer:
The solution is the point (3, -1)
Step-by-step explanation:
We have the system of equations:
x = 3
y + 1 = 0
To solve this graphically, we need to graph these two lines and see in which point the lines intersect.
To graph the line x = 3, we need to draw a vertical line that passes through x = 3.
To graph y + 1 = 0
First we should isolate y.
y = -1
This is graphed as a horizontal line that passes through y = -1
The graph of these two lines can be seen in the image below.
Where the green line is x = 3, and the blue line is y = -1
Now, looking at the graph we can see that the lines do intersect in the point (3, -1)
Then the solution of the system is the point (3, -1)
![[tex]\left \{ {{x=3} \atop {y+1=0}} \right.[/tex] solve graphically this linear system of equations](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/AEr9r0IZ5mjNAIt4LjQW1oPlkO6mn8Jv.png)
Factor the quadratic by checking factor pairs. \(8x^{2} +6x + 1\)
Answers
Answer:
=(2x+1)(4x+1)
Kevin played a trivia game. Each correct answer is worth 2 / points, and each incorrect answer is worth ⎯/ point. What was Kevin’s score?
Answers
Step-by-step explanation:
so if he answer correct he get 2 points but incorrect answer he get 0 so his points are 0 because he did not play a game
1 Use the guidelines opposite to rewrite these expressions.
a) - 2a + 5c
Answers
The opposite expression of "-2a + 5c" is "5c - 2a".
To rewrite the expression "-2a + 5c" using the guidelines opposite, we will reverse the steps taken to simplify the expression.
Reverse the order of the terms: 5c - 2a
Reverse the sign of each term: 5c + (-2a)
After following these guidelines, the expression "-2a + 5c" is rewritten as "5c + (-2a)".
Let's break down the steps:
Reverse the order of the terms
We simply switch the positions of the terms -2a and 5c to get 5c - 2a.
Reverse the sign of each term
We change the sign of each term to its opposite.
The opposite of -2a is +2a, and the opposite of 5c is -5c.
Therefore, we obtain 5c + (-2a).
It is important to note that the expression "5c + (-2a)" is equivalent to "-2a + 5c".
Both expressions represent the same mathematical relationship, but the rewritten form follows the guidelines opposite by reversing the order of terms and changing the sign of each term.
For similar question on opposite expression.
https://brainly.com/question/3426818
#SPJ8
Solve for the value of the variables below

Answers
Answer:
x = 80
Step-by-step explanation:
degrees in pentagon = 540
120 + 100 + (180-40) + (180-80) + x = 540
120 + 100 + 140 + 100 + x = 540
x = 80
Answer:
80°
Step-by-step explanation:
First, find the total interior angle by using the formula (n - 2) × 180
In this formula, n = the number of sides.
Find all the missing interior angles.
Add all the interior angles.
Subtract the that value from the total interior angle.
I need help and I’ll mark you as a brainliest

Answers
Answer:
the top one is 30 the second one is 60.22 the third one is 66.7 the forth one is 59.8
Which describes the graph of the inequality g(x)>2√3x+2?
A. Shading above a solid line
B. Shading above a dotted line
C. Shading below a dotted line
D. Shading below a solid line
Answers
Answer:
A. Shading above a solid line.
Step-by-step explanation:
Let \(f(x) = 2\sqrt{3}\cdot x + 2\), whose domain is all real numbers, since it is a first order polynomial (linear function) and meaning that for all element of \(x\) exists one and only one value for \(f(x)\), meaning a solid line. If \(g(x) > f(x)\), then the range of all possible results is a shade area above the solid line.
Hence, the correct answer is A.
10 POINTTSSS answer fast The formula a = m − n represents the actual cost, a, of an item with original price m after a coupon for n dollars off is applied. Solve the formula for the amount of the coupon. Group of answer choices n=m−a n = a − m n = −m − a n=a+m
Answers
Answer:
n = m - a
Step-by-step explanation:
Given:
a = m − n
Where,
Actual cost of the item = a
Original price of the item = m
Amount of Coupon = n
Solve the formula for the amount of the coupon
Making n the subject
a = m − n
Subtract m from both sides
a - m = m - n - m
a - m = - n
Divide both sides by -1
(a - m) / -1 = -n / -1
- a + m = n
Can also be written as
n = m - a
A student sketched some art on an 8.5 inch x 11 inch piece of paper. She wants to resize it to fit an 8 inch x 10 inch frame (as shown below)
What percent of the original sketch was still able to be included in the frame?
A. 75.2%
B. 85.6%
C. 93.8%
D. 96.6%
Answers
Answer:
B. 85.6%
Step-by-step explanation:
Since we want to find the percentage, which is essentially a fraction, we will divide the area of the smaller frame by the area of the larger paper.
The paper and frame are both rectangles, so the area of a rectangle is denoted by A = lw, where l is the length and w is the width.
For the paper, the length is l = 8.5 and the width is w = 11. So:
A = lw
A = 8.5 * 11 = 93.5 inches squared
For the frame, the length is l = 8 and the width is w = 10. So:
A = lw
A = 8 * 10 = 80 inches squared
The percentage of the original sketch included in the frame would be:
(80 / 93.5) * 100 ≈ 85.6%
The answer is thus B.
~ an aesthetics lover
Answer:
The answer should be B. 85.6% hopefully this helped you!
Step-by-step explanation:
Solve the equation p + 5 = −12 for p.
Answers
Answer: 17
Explanation
P-5=12
Transpose 5 to the other side
It will become +5 after transposing becuase it was -5 before transposing
P=12+5
P=17
PLSSS MARK AS BRAINLIEST
So, what is easy to do is count 5 up from 12. Which would be 17. But because it’s negative, you’d have to say:
-17 + 5 = -12!
?????????????????????????

Answers
Answer:
The answer is D
Step-by-step explanation:
x√{5^2+8^2}=√89
Answer:
\(\boxed{\tt x=\sqrt{89} }\)
Step-by-step explanation:
We'll use the Pythagorean Theorem
Equation: \(\tt a^2+b^2=c^2\)
where a and b are the lengths of the two legs of triangle, and c is the hypotenuse.
\(\tt a=5\)\(\tt b=8\)\(\tt c=x\)*A and b can be switched because they are legs*
\(\tt a^2+b^2=c^2\)
Plug in the side lengths:
\(\tt 5^2+8^2=x^2\)
Evaluate 5^2 and 8^2:
\(\tt 25+64=x^2\)
Add 25 and 64 = 89
\(\tt 89=x^2\)
Now, take the square root of each side:
\(\tt x=\sqrt{89} \)
_____________________________
A circular tabletop has a diameter of 2.1 m.
a) What is the area?
b) The table is to be painted. One tin of paint can cover an area of 1.75 m² and cost 5.50 dollars.
ii)How any tins of paint must be bought?
iii) How much will it cost for materials and labour is 2/3 the cost of materials?
Answers
Answer:
Step-by-step explanation:
Area of Circle:a) Diameter = 2.1 m
r = 2.1 ÷ 2 = 1.05 m
Area = πr²
= 3.14 * 1.05 * 1.05
= 3.46 = 3.5 m²
b) To find the number of paint tins, divide the area of table top by 1.75 m²
Number of tins = 3.5 ÷ 1.75
= 2 tins
c) Cost of 1 tin = $ 5.50
Cost of 2 tin = 2 *5.50
= $ 11
\(\sf d) Cost\ of \ labour = \dfrac{2}{3} * 11\)
= $ 7.30
Answer:
a=3.46 (2dp) b(ii)=2
Step-by-step explanation:
a)
πr²=area
2.1/2 = 1.05 as the radius
1.05² x π= 3.46 (2dp)
b)
3.46/1.75= 1.98
1.98 can be changed into two
∴ 2 tins will be needed
Determine the quotient: 5 3/5 ÷ 7 1/3 I need the answer Plus showing work
Answers
The quotient of the fractions is 42/55
How to determine the quotient of fractions?
The quotient of a fraction is the value that is obtained when you simplify the fraction
Given: 5 3/5 ÷ 7 1/3
5 3/5 = 28/3 and 7 1/3 = 22/3
5 3/5 ÷ 7 1/3 = 28/5 ÷ 22/3
= 28/5 × 3/22
= 84/110
= 42/55
Thus, the quotient is 42/55
Learn more about fractions on:
brainly.com/question/11562149
#SPJ1
14) The freezing point of a solution of 100.0mg of Eicosene (a molecular compound and a nonelectrolyte) in 1.00 g of benzene was lower by 1.87∘C than the freezing point of pure benzene. Determine the molar mass of Eicosene. Note: K f(benzene) =4.90∘C/m.
Answers
Therefore, the molar mass of Eicosene is approximately 0.339 g/mol.
To determine the molar mass of Eicosene, we can use the freezing point depression equation:
ΔT = Kf * m * i
where:
ΔT = freezing point depression
Kf = freezing point depression constant for the solvent (benzene)
m = molality of the solute
i = van't Hoff factor (for molecular compounds, i = 1)
Given:
ΔT = -1.87 °C
Kf (benzene) = 4.90 °C/m
m = molality of Eicosene in benzene
molar mass of benzene = 78.11 g/mol
mass of Eicosene = 100.0 mg = 0.1000 g
mass of benzene = 1.00 g
First, we need to calculate the molality (m) of Eicosene in benzene. Molality is defined as the number of moles of solute per kilogram of solvent.
molality (m) = moles of solute / mass of solvent (in kg)
To calculate the moles of Eicosene, we need to convert the mass of Eicosene to moles using its molar mass. Let's assume the molar mass of Eicosene is M g/mol.
moles of Eicosene = mass of Eicosene / molar mass of Eicosene
moles of Eicosene = 0.1000 g / M g/mol
Now, we can calculate the molality (m) using the moles of Eicosene and the mass of benzene.
m = moles of Eicosene / mass of benzene (in kg)
m = (0.1000 g / M g/mol) / (1.00 kg / 78.11 g/mol)
Simplifying, we get:
m = 0.1000 / (M * 78.11)
Now, we can substitute the values into the freezing point depression equation and solve for the molar mass (M).
ΔT = Kf * m * i
-1.87 = 4.90 * (0.1000 / (M * 78.11)) * 1
Simplifying, we get:
-1.87 = 0.049 / (M * 78.11)
To solve for M, rearrange the equation:
M = 0.049 / (-1.87 * 78.11)
M ≈ 0.000339 mol/g
Finally, convert the molar mass to grams per mole:
M ≈ 0.339 g/mol
To know more about molar mass,
https://brainly.com/question/33301497
#SPJ11
Write an equation of the line passing through the points (3,4) and (-2, -16)
Answers
Answer:
y=4x-8
Step-by-step explanation:
Slope= y1-y2/x1-x2
Slope = 4- (-16)/3-(-2)=4+16/3+2=20/5=4
Equation: y=4x+b
Let y=4 and x=3
4=12+b
b= -12+4
b=-8
Therefore: y=4x-8