Carlos and his family left for the amsuement park at 8:35
a.M. The trip took 1 hour and 55 minutes. What time did they arrive
Answers
Related Questions
5 times the difference of a number and 7
Answers
Answer:
5(n-7)
Step-by-step explanation:
a card is drawn randomly from a standard 52-card deck. find the probability of the given event. (a) the card drawn is 3 the probability is : (b) the card drawn is a face card (jack, queen, or king) the probability is : (c) the card drawn is not a face card. the probability is :
Answers
A card is drawn randomly from a standard 52-card deck. then the probabilities are a) 1/13 b) 3/13 and c) 10/13
There are four 3's in the deck. This means that, from 52 possible cards to drawn, we have 4 chances of drawing a 3. This means that the probability will be:
p = 4/52
p= 1/13
b.
For every suit, there are three face cards, J, Q and K. There are 4 suits, so, the total number of face cards its:
4*3 =12
The total possible cards are, still, 52, so, the probability will be
p= 12/52
p=3/13
c.
We know that the card drawn must be a face card, o not being a face card. There is no third choice here. So, the probability of drawing a face card OR not drawing a face card its:
p=52/52
p=1
so
p( the card is a face card ) + p( the card is not a face card) =1
but, we know that
p( the card is a face card ) =3/13
so
p( the card is not a face card) =1- 3/13
= 10/13
learn more about of probability here
https://brainly.com/question/13293035
#SPJ4
A runner sprinted for 189 yards (yd). How many feet (ft) is this?
First fill in the blank on the left side of the equation using one of the ratios. Then write your answer on the right side of the equation.
Ratios:
3 ft
1 yd
189 yd
1
1 yd
3 ft
1760 yd
1 mi
Al mi
1760 yd
1 ft
12 in
12 in
1 ft
ft yd
8
X
in
5
mi

Answers
Answer:
567 ft
Step-by-step explanation:
1 yd = 3 ft
1 yd is to 3 ft as 189 yd is to x ft
1/3 = 189/x
1 × x = 3 × 189
x = 567
567 ft
5. What is "Data Triangulation" in general? Give 2 real-world examples.
Answers
Data triangulation is a research method that involves using multiple data sources or methods to gather and analyze information, enhancing the validity and comprehensiveness of findings.
Data triangulation is a research method that involves using multiple sources or methods to gather and analyze data on a particular topic or research question. By combining different data sources, researchers aim to enhance the validity, reliability, and comprehensiveness of their findings.
Two real-world examples of data triangulation are:
Qualitative-Quantitative Triangulation in Market Research: In market research, qualitative methods like focus groups or interviews can be combined with quantitative methods like surveys or sales data analysis. By triangulating these data sources, researchers can gain a deeper understanding of consumer preferences, behaviors, and market trends, combining the richness of qualitative insights with the statistical power of quantitative data.Methodological Triangulation in Educational Research: In educational research, methodological triangulation can be employed by using multiple research methods to investigate a learning phenomenon. For example, a researcher may use classroom observations, interviews with teachers, and student performance data to gain a comprehensive understanding of a teaching strategy's effectiveness. By triangulating these data sources, the researcher can capture a more complete picture of the learning environment and draw robust conclusions.Learn more about Data Triangulation at
https://brainly.com/question/30027711
#SPJ4
let f = x3i y3j z3k. evaluate the surface integral of f over the unit sphere.
Answers
The surface integral of f over the unit sphere is (4π/15) (3 k), where k is the unit vector in the z-direction. The answer is independent of the specific parameterization of the sphere and only depends on the surface itself.
To evaluate the surface integral of f over the unit sphere, we need to use the formula:
∫∫S f · dS = ∫∫R f(φ,θ) · ||r(φ,θ)|| sin(φ) dφdθ
Where S is the surface of the unit sphere, R is the region in the parameter domain (φ,θ) that corresponds to S, ||r(φ,θ)|| is the magnitude of the partial derivative of the position vector r(φ,θ), and sin(φ) is the Jacobian factor.
For the unit sphere, we have:
x = sin(φ) cos(θ)
y = sin(φ) sin(θ)
z = cos(φ)
So, we can find the partial derivatives:
r_φ = cos(φ) cos(θ) i + cos(φ) sin(θ) j - sin(φ) k
r_θ = -sin(φ) sin(θ) i + sin(φ) cos(θ) j
Then, we can compute the magnitude:
||r_φ x r_θ|| = ||sin(φ) cos(φ) cos(θ) j + sin(φ) cos(φ) sin(θ) (-i) + sin^2(φ) k|| = sin(φ)
Now, we can substitute into the formula and evaluate the integral:
∫∫S f · dS = ∫0^π ∫0^2π (sin^3(φ) cos^3(θ) i + sin^3(φ) sin^3(θ) j + sin^3(φ) cos^3(φ) k) · sin(φ) dφdθ
= ∫0^π ∫0^2π sin^4(φ) (cos^3(θ) i + sin^3(θ) j + cos^3(φ) k) dφdθ
To integrate over θ, we can use the fact that cos^3(θ) and sin^3(θ) are odd functions, so their integral over a full period is zero. Thus, we get:
∫∫S f · dS = ∫0^π (1/5) sin^5(φ) (3 cos^3(φ) k + 2 sin^3(φ) i + 2 cos^3(φ) j) dφ
= (4π/15) (3 k)
Therefore, the surface integral of f over the unit sphere is (4π/15) (3 k), where k is the unit vector in the z-direction. The answer is independent of the specific parameterization of the sphere and only depends on the surface itself.
Learn more on surface integral here:
https://brainly.com/question/15177673
#SPJ11
State whether the data described below are discrete or continuous, and explain why.
- The exact heights of different elephants. Choose the correct answer below.
A. The data are continuous because the data can take on any value in an interval.
B. The data are discrete because the data can only take on specific values.
C. The data are continuous because the data can only take on specific values.
D. The data are discrete because the data can take on any value in an interval.
Answers
Answer:
The correct answer:
The data are continuous because the data can take on any value in an interval. (A)
Step-by-step explanation:
There are two categories of data:
Discrete data: These are data that have specific values that they can take on. There are limits to what values can be assigned to such categories. for example, The number of countries in a continent, there can either be 15 countries, 50 countries 30 countries, etc. There is not a possibility of having 40.56 countries on this kind of list. hence it is a discrete dataset.
Continuous data are data that can take on any value within an interval or on a particular scale of measurement. In this example, the height of the elephant in meters can be 1.5m, 2m, 1.06m, etc. There is no limit to the possibility of the height of an elephant on a meter scale.
What is the Y intercept of the linear equation X -1/2 Y equals -6
Answers
Answer:
y=12
Step-by-step explanation:

6. Yu is considering two different banks for his $3,000 savings account: OPTION A 4% FOR 20 YEARS SIMPLE INTEREST OPTION B 2% FOR 10 YEARS COMPOUND INTEREST 8 What is the interest earned on option A? O What is the total value on option A? What is the interest earned on option B? O What is the total value on option B? 10 Which is the better option?
Answers
The interest earned on Option A is $2400 and Option B is $666.18. Option A is the better option as Option A has a higher total value of $5400 compared to Option B's total value of $3666.18.
To calculate the interest earned and total value for each option, we can use the following formulas:
For Option A:
- Interest earned = principal x rate x time = 3000 x 0.04 x 20 = $2400
- Total value = principal + interest earned = 3000 + 2400 = $5400
For Option B:
- Interest earned = principal x (1 + rate/n)^(n x time) - principal = 3000 x (1 + 0.02/1)^(1 x 10) - 3000 = $666.18
- Total value = principal + interest earned = 3000 + 666.18 = $3666.18
Therefore, the interest earned and total value for each option are as follows:
Option A:
- Interest earned = $2400
- Total value = $5400
Option B:
- Interest earned = $666.18
- Total value = $3666.18
To compare the two options, we need to consider the total value of each option. Option A has a higher total value of $5400 compared to Option B's total value of $3666.18. Therefore, Option A is the better option.
To know more about total value, visit:
https://brainly.com/question/30910643#
#SPJ11
Which functions are a specific type of piecewise-defined functions?Quadratic functionsAbsolute value functionsCubic functionsLinear functions
Answers
Solution
The answer is
Absolute Value Function
now say you sample 10 independent customers. what is the probability that less than or equal to 5 (five) of them will take more than 3 minutes to check out their groceries? round to the nearest hundredths/second decimal place,
Answers
The probability that less than or equal to 5 of the 10 independent customers will take more than 3 minutes to check out their groceries is approximately 0.9245.
To calculate this probability, we can use the binomial probability formula. Let's denote X as the number of customers taking more than 3 minutes to check out. We want to find P(X ≤ 5) when n = 10 (number of trials) and p (probability of success) is not given explicitly.
Step 1: Determine the probability of success (p).
Since the probability of each customer taking more than 3 minutes is not provided, we need to make an assumption or use historical data. Let's assume that the probability of a customer taking more than 3 minutes is 0.2.
Step 2: Calculate the probability of X ≤ 5.
Using the binomial probability formula, we can calculate the cumulative probability:
P(X ≤ 5) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5)
P(X ≤ 5) = C(10, 0) * p^0 * (1 - p)^(10 - 0) + C(10, 1) * p^1 * (1 - p)^(10 - 1) + C(10, 2) * p^2 * (1 - p)^(10 - 2) + C(10, 3) * p^3 * (1 - p)^(10 - 3) + C(10, 4) * p^4 * (1 - p)^(10 - 4) + C(10, 5) * p^5 * (1 - p)^(10 - 5)
Substituting p = 0.2 into the formula and performing the calculations:
P(X ≤ 5) ≈ 0.1074 + 0.2686 + 0.3020 + 0.2013 + 0.0889 + 0.0246
P(X ≤ 5) ≈ 0.9928
Rounding this probability to the nearest hundredth/second decimal place, we get approximately 0.99. However, the question asks for the probability that less than or equal to 5 customers take more than 3 minutes, so we subtract the probability of all 10 customers taking more than 3 minutes from 1:
P(X ≤ 5) = 1 - P(X = 10)
P(X ≤ 5) ≈ 1 - 0.9928
P(X ≤ 5) ≈ 0.0072
Therefore, the probability that less than or equal to 5 customers out of 10 will take more than 3 minutes to check out their groceries is approximately 0.0072 or 0.72%.
For more questions like Probability click the link below:
https://brainly.com/question/11234923
#SPJ11
i need steps on how to solve this

Answers
Answer: Wow, sorry it took me so long, but I believe your answer is 127.
Step-by-step explanation: When finding an angle for something like this, we need to find the angles of the triangle. As you can see, 89 is provided already, but we need two more. Let's say we make a guess of 127 as 14x + 1. The other side which is angle F has to add up with 127 to make 180, which is 53. So angle F is 53. That gives us 89 + 53 which equals 142. 180 - 142 equals 38. To solve 5x - 7, you need to fill in 9 to make the equation true, which is 5 x 9 - 7 or 38. So, angle H is 38. 38 + 89 + 53 equals 180. So for 14x + 1, it's 127.
Hope this helps! :)
The quotient of y and 3 added to 9 equals 10
Answers
Answer:
Step-by-step explanation:
Are you after a solution for y?
quotient of y and 3 is a fancy word for division
y/3+9=10
To solve for y subtract 9 from both sides
y/3+9-9=10-9
y/3=1
To solve for y
multiply both sides by 3
3(y/3)=1*3
y=3
Given MTWBGK, find the values of x and y.
B
G
T (4x-3)*
45°
(11y + 6)²
M
K
41
W
Answers
The values of x and y are x = 6, y = 5.
First, we can identify that angle T is a right angle, as it is marked with a square symbol. We can use this information to set up the following equation: (4x - 3)² + (11y + 6)² = 41²
Next, we can use the fact that there are two pairs of congruent sides in a kite to find the values of x and y. Specifically, we can use the fact that BG and KT are congruent, as well as MT and WG.
Since angle T is a right angle, we know that angle MTG is also a right angle, and therefore triangle MTG is a right triangle. We can use the Pythagorean theorem to set up an equation: (4x - 3)² + (11y + 6)² = MG²
We can also use the fact that BG and KT are congruent to set up another equation: (4x - 3) = (11y + 6)
Solving this system of equations gives us: x = 6, y = 5
Substituting these values back into the original equation, we can verify that it holds true. Therefore, the values of x and y are 6 and 5, respectively.
For more questions like Equation click the link below:
https://brainly.com/question/29657983
#SPJ11
exercise 6.1.11: find the inverse laplace transform of 1 /(s−1)^2 (s+1) .
Answers
Answer:
The inverse Laplace transform of 1/(s-1)^2 (s+1) is e^t - te^t + e^(-t)
We start by applying partial fraction decomposition to the given expression:
1/(s-1)^2 (s+1) = A/(s-1) + B/(s-1)^2 + C/(s+1)
Multiplying both sides by the denominator, we get:
1 = A(s-1)(s+1) + B(s+1) + C(s-1)^2
Substituting s=1 gives:
1 = 4C
So, C=1/4.
Substituting s=-1 gives:
1 = -4A
So, A=-1/4.
Substituting s=1 and simplifying gives:
B = 1/2.
Thus, we have:
1/(s-1)^2 (s+1) = (-1/4)/(s-1) + (1/2)/(s-1)^2 + (1/4)/(s+1)
Taking the inverse Laplace transform of each term using the table of Laplace transforms, we get:
L^(-1){(-1/4)/(s-1)} = -e^t
L^(-1){(1/2)/(s-1)^2} = te^t
L^(-1){(1/4)/(s+1)} = (1/2)e^(-t)
Hence, the inverse Laplace transform of 1/(s-1)^2 (s+1) is e^t - te^t + e^(-t).
Learn more about laplace tranform:
https://brainly.com/question/30759963
#SPJ11
+
Complete the fraction calculation below
3/8 + 1/6
Answers
Answer:
\(\frac{13}{24}\)
Step-by-step explanation:
=> \(\frac{3}{8} +\frac{1}{6}\)
LCM = 24
=> \(\frac{9+4}{24}\)
=> \(\frac{13}{24}\)
Answer:
\(\frac{13}{24}\)
Step-by-step explanation:
\(\frac{3}{8} +\frac{1}{6}\)
\(\frac{3 \times 6}{8\times 6} +\frac{1\times8}{6\times8}\)
\(\frac{18}{48} +\frac{8}{48}\)
\(\frac{18+8}{48}\)
\(\frac{26}{48}\)
\(\frac{13}{24}=0.54166...\)
Please helppppppppp!!!!!
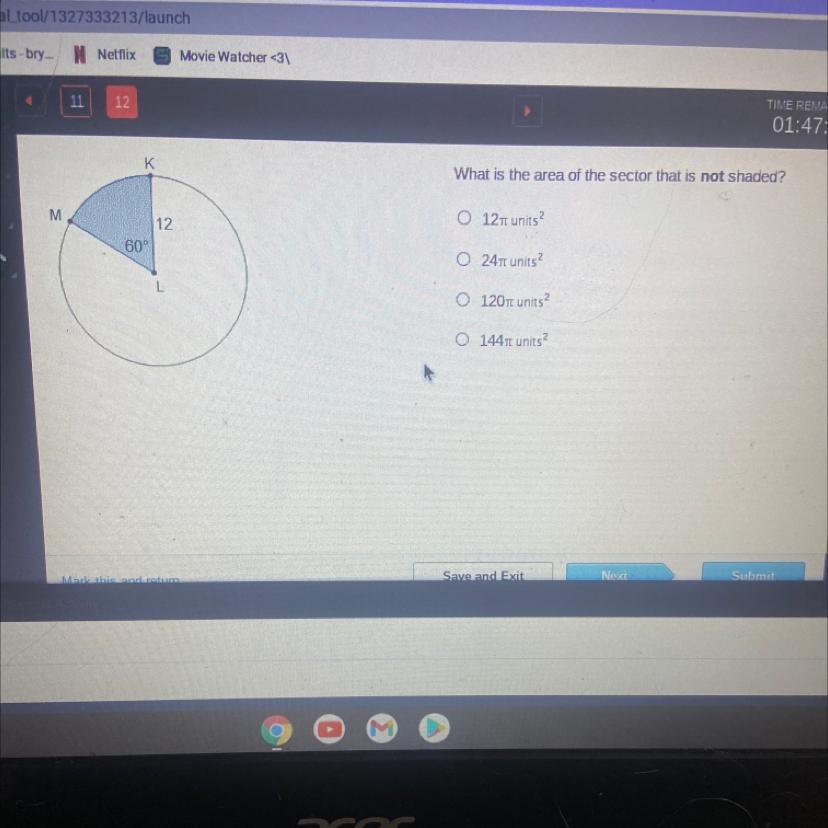
Answers
7. suppose a binary digit (0 or 1) needs to be transmitted across a series of 4 channels. each time, the digit is transmitted correctly to the next channel with probability 0.9, and is transmitted incorrectly (meaning that 1 is transmitted as 0, and 0 is transmitted as 1) with probability 0.1. if the digit 0 is sent, what is the probability that the digit that is received (after having been transmitted across the 4 channels) is a 0?
Answers
The probability that the digit that is received (after having been transmitted across the 4 channels) is 0.3645
In communication systems, it is common to face the challenge of transmitting information accurately over a noisy channel. In this scenario, errors can occur during transmission, and it is essential to quantify the probability of receiving the correct information at the end of the channel.
In this problem, we are asked to calculate the probability that the digit received after transmitting a 0 across four channels is also a 0. We know that each channel can either transmit the digit correctly with probability 0.9 or incorrectly with probability 0.1. Therefore, we can use the concept of conditional probability to solve this problem.
Using Bayes' theorem, we can rewrite this as:
P(CCCC | 0 received) x P(0 received) / P(CCCC)
Here, P(CCCC | 0 received) represents the probability that all four channels transmitted the 0 correctly, given that a 0 was received. This probability can be calculated as:
P(CCCC | 0 received) = P(C) x P(C | C) x P(C | C | C) x P(C | C | C | C)
Substituting the given probabilities, we get:
P(CCCC | 0 received) = 0.9 * 0.9 * 0.9 * 0.9 = 0.6561
Similarly, we can calculate the probability of receiving a 0 in general as:
P(0 received) = P(CCCC | 0 received) x P(0) + P(IIII | 0 received) x P(1)
where P(IIII | 0 received) represents the probability that all four channels transmitted the digit incorrectly, given that a 0 was received. This probability can be calculated similarly as:
P(IIII | 0 received) = P(I) * P(I | I) x P(I | I | I) x P(I | I | I | I) = 0.1 x 0.1 x 0.1 x 0.1 = 0.0001
Substituting the given probabilities, we get:
P(0 received) = 0.6561 x 0.5 + 0.0001 x 0.5 = 0.3281
Finally, we can calculate the denominator P(CCCC) as:
P(CCCC) = P(CCCC | 0 received) x P(0) + P(CCCC | 1 received) x P(1)
where P(CCCC | 1 received) represents the probability that all four channels transmitted the digit correctly, given that a 1 was received. This probability can be calculated similarly as:
P(CCCC | 1 received) = P(I) x P(I | C) x P(I | C | C) x P(I | C | C | C) = 0.1 x 0.9 x 0.9 x 0.9 = 0.0729
Substituting the given probabilities, we get:
P(CCCC) = 0.6561 * 0.5 + 0.0729 * 0.5 = 0.3645
To know more about probability here.
https://brainly.com/question/11234923
#SPJ4
Without using a calculator, order the following expressions from least to greatest.

Answers
The ascending order of the expressions are π/3 , √8/3 , √4/2
Given data ,
Let the expression be represented as A
Now , the value of A is
A = π/3 , √8/3 , √4/2
On simplifying , we get
Now , π > √8
So , the value of π/3 is greater than √8/4 since they have the same denominator
And , the value of √4/2 = 1
Hence , the ascending order is √4/2 , √8/3 , π/3
To learn more about ascending order click :
https://brainly.com/question/20681445
#SPJ1
A textbook store sold a combined total of 364 chemistry and psychology textbooks in a week. The number of psychology textbooks sold was 56 less than the number of chemistry textbooks sold. How many textbooks of each type were sold?
Answers
3. The relationship between the cost of a corsage and the number of flowers in the corsage is shown
below.
Number of Cost of
Flowers, 1 Corsage, c
2.
$7.00
3
$10.50
4
$14.00
5
$17.50
Which statement is true about the information in the table?
A The information in the table has a constant rate of change of 3.5.
B The information in the table has a constant rate of change of 2
C The information in the table has a constant rate of change of 7
D The information in the table does not have a constant rate of change
Answers
Answer:
A The information in the table has a constant rate of change of 3.5.
Step-by-step explanation:
A linear equation is in the form y = mx + b, where y is a dependent variable, x is an independent variable, m is the rate of change (slope) and b is the value of y when x = 0.
Let y represent the cost of a corsage and x represent the number of flowers in the corsage
The table (x, y) has the points (2, 7) and (3, 10.5). The equation is given by:
\(y-y_1=\frac{y_2-y_1}{x_2-x_1} (x-x_1)\\\\y-7=\frac{10.5-7}{3-2}(x-2)\\\\y-7=3.5(x-2)\\\\y-7=3.5x-7\\\\y=3.5x\)
Therefore the rate of change is 3.5
The hypotenuse of a right triangle measures 14 cm and one of its legs measures 6 cm.
Find the measure of the other leg. If necessary, round to the nearest tenth.
Answers
Explanation: if you use the Pythagorean theorem: a^2+ b^2 = c2, you would plug in 14 for c and 6 for a. Giving you
6^2+b^2=14^2
Simplify this and you would get:
36 + b^2 = 196
Subtract 36 from both sides getting you:
B^2= 160
Take the square root of both sides getting you your final answer of:
B= 40.
help imma need those answers

Answers
Answer:
y=1/2x
Step-by-step explanation:
It looks like it
please help i beg i never get these right

Answers
Answer:
\(\sin(105) = \frac{\sqrt 2 + \sqrt 6}{4}\)
Step-by-step explanation:
Given
\(\sin(105^o)\)
Required
Solve
Using sine rule, we have:
\(\sin(A + B) = \sin(A)\cos(B) + \sin(B)\cos(A)\)
This gives:
\(\sin(105^o) = \sin(60 + 45)\)
So, we have:
\(\sin(60 + 45) = \sin(60)\cos(45) + \sin(45)\cos(60)\)
In radical forms, we have:
\(\sin(60 + 45) = \frac{\sqrt 3}{2} * \frac{\sqrt 2}{2} + \frac{\sqrt 2}{2} * \frac{1}{2}\)
\(\sin(60 + 45) = \frac{\sqrt 6}{4} + \frac{\sqrt 2}{4}\)
Take LCM
\(\sin(60 + 45) = \frac{\sqrt 6 + \sqrt 2}{4}\)
Rewrite as:
\(\sin(60 + 45) = \frac{\sqrt 2 + \sqrt 6}{4}\)
Hence:
\(\sin(105) = \frac{\sqrt 2 + \sqrt 6}{4}\)
For the following set of data, find the number of data within 1 population standarddeviation of the mean.68 68 70 61 67 71 63 67
Answers
68 68 70 61 67 71 63 67
Step 1: Write the formula of standard deviation
\(\text{Stanadard deviation = }\sqrt[]{\frac{Sum(x\text{ - }\mu)^2}{n}}\)\(\begin{gathered} \text{Where } \\ n\text{ = number of data } \\ \mu\text{ = mean} \end{gathered}\)n = 8
Step 2: Find the mean
\(\begin{gathered} \operatorname{mean}\text{ }\mu\text{ = }\frac{\sum ^{}_{\text{ }}x}{n} \\ \mu\text{ = }\frac{68\text{ + 86 + 70 + 61 + 67 + 71 + 63 + 67}}{8} \\ \mu\text{ = }\frac{535}{8} \\ \mu\text{ = 66.9} \end{gathered}\)Step 3: find the standard deviation
Next, substitute to find the standard deviation
\(\begin{gathered} \text{standard deviation = }\sqrt[]{\frac{sum(x\text{ - }\mu)^2}{n}} \\ =\text{ }\sqrt[]{\frac{78.88}{8}} \\ =\text{ }\sqrt[]{9.86} \\ =\text{ 3.14} \end{gathered}\)standard deviation = 3.14
Final answer
The number of data within the standard deviation of the mean = 5


What value is printed by the code below? What value is printed by the code below? count \( =0 \) if count \(
Answers
The code initializes the variable `count` to 0. Then, it enters a while loop that continues as long as `count` is less than 11. The value printed by the code is: 1
The value printed by the code is:
1
2
3
4
5
6
7
8
9
10
11
The code initializes the variable `count` to 0. Then, it enters a while loop that continues as long as `count` is less than 11. Inside the loop, `count` is incremented by 1, and then the current value of `count` is printed. This process repeats until `count` reaches 11.
Therefore, the numbers from 1 to 11 (inclusive) are printed.
The value printed by the code is:
1
In the second code, after initializing `count` to 0, the if statement checks if `count` is less than 11. Since the condition is true (`count` is 0), the code enters the if block. Inside the block, `count` is incremented by 1 and then printed. After executing the if block once, the code exits, and only the value 1 is printed.
Learn more about code here:
https://brainly.com/question/24735155
#SPJ11
The complete question is:
What value is printed by the code below? count = 0 while count < 11: count = count + 1 print(count) What value is printed by the code below? count = 0 if count < 11: count = count + 1 print(count)?
what is the slope-intercept form of the equation 2x + y = 4?

Answers
slope intercept form: y = -2x + 4
Explanation:\(\sf slope \ intercept \ form: y = mx + b\)
where m is slope, b is y-intercept
=============================
\(\rightarrow \sf 2x + y = 4\)
\(\rightarrow \sf y = 4-2x\)
\(\rightarrow \sf y = -2x +4\)
Now, identify slope: -2, y-intercept: 4
Answer:
The slope-intercept form is y=mx+b y = m x + b , where m is the slope and b is the y-intercept.
Rewrite in slope-intercept form. Subtract 2 x from both sides of the equation. Multiply each term in −y=4−2x - y = 4 - 2 x by −1 - 1 .
Step-by-step explanation:
Pls help me answer this question if correct I'll make brainylist!!!!

Answers
Answer:
32
Step-by-step explanation:
Need help with these 3

Answers
Answer:
Step-by-step explanation:
Corresponding angles: When two parallel lines are intersected by a transversal, the acute angles on the same side are congruent & the obtuse angles on the same side of the transversal are congruent and they are called corresponding angles.
Co-interior angles: The interior angles on the same side of the transversal are called co -interior angles and they are supplementary.
a) c + 123 = 180 {linear pair}
c = 180 - 123
c = 57
a = 123 {Corresponding angles}
b = a {Vertically opposite angles are congruent}
b = 123
b) f + 82 = 180 {Linear pair}
f = 180 - 82
f = 98
d = f {Corresponding angles}
d = 98
e = d {Vertically opposite angles}
e = 98
c) h = 75 {Corresponding angles}
g = h {Vertically opposite anges}
g = 75
What is 5 divided by (-3) but in the long division?
Answers
Answer:
Step-by-step explanation:
Divide 5 by 3
5 divided by 3 is 1 (in the set of integers). The remainder is 2.
5/3 is 1.666666666666666666666666666666666666666666666666666666666666667 (in the set of reals).
Solution for 5 divided by 3
✍️See below how to solve this division manually.
5 divided by 3 - Long Division Solution
The solution below uses the "Long Division With Remainders Method". It is one of two existing methods of doing long division.
Start by setting the divisor 3 on the left side and the dividend 5 on the right:
1 ⇐ Quotient
―
3)5 ⇐ Dividend
3
-
2 ⇐ Remainder
The result of the division of 5 divided by 3 is 1.6666666666666667, as a decimal number.
5/3 as a mixed number
5 divided by 3 equals to the mixed number 1 2
3
.
Note that the result of the division 5÷3 is not an exact value and is equivalent to a recurring decimal 1.66... (which has 6 as the period).
y = -3x + 5
2x + y = 6
solve using substitute please
Answers
Answer:(3,-1)
Step-by-step explanation: