Capture-recapture studies are common in ecology. One form of the study is conducted as follows. Suppose we have a population of N deer in a study area. Initially n deer from this population are captured, marked so that they can be identified as having been captured, and returned to the population. After the deer are allowed to mix together, m deer are captured from the population and the number k of these deer having marks from the first capture is observed.
Required:
Assuming that the first and second captures can be considered random selections from the population and that no deer have either entered or left the study area during the sampling period, what is the probability of observing k marked deer in the second sample of m deer?
Answers
The probability of observing k marked deer in the second sample of m deer can be calculated using the hypergeometric distribution.
The probability of observing k marked deer in the second sample of m deer in a capture-recapture study can be calculated using the concept of hypergeometric distribution.
In this scenario, let's consider the following variables:
N = Total population size (number of deer)
n = Number of deer initially captured and marked
m = Number of deer captured in the second sample
k = Number of deer in the second sample that are marked from the first capture
The probability of observing k marked deer in the second sample can be calculated as the ratio of two combinations:
P(k marked in the second sample) = (Number of ways to choose k marked deer) * (Number of ways to choose (m - k) unmarked deer) / (Number of ways to choose m deer from the population)
The number of ways to choose k marked deer from the total n marked deer in the population is given by the combination formula:
Number of ways to choose k marked deer = C(n, k)
Similarly, the number of ways to choose (m - k) unmarked deer from the remaining (N - n) unmarked deer in the population is given by the combination formula:
Number of ways to choose (m - k) unmarked deer = C(N - n, m - k)
Lastly, the number of ways to choose m deer from the total N deer population is given by the combination formula:
Number of ways to choose m deer from the population = C(N, m)
Putting it all together, the probability of observing k marked deer in the second sample can be calculated as:
P(k marked in the second sample) = C(n, k) * C(N - n, m - k) / C(N, m)
This formula takes into account the random selection of deer in the two samples and assumes no change in the population size or migration during the sampling period.
It's important to note that this calculation assumes that the marking and recapture process does not affect the behavior or mortality of the deer. It also assumes that the marked deer mix randomly with the unmarked deer between the captures.
By using the appropriate combination formulas and plugging in the values of n, N, m, and k, you can calculate the probability of observing k marked deer in the second sample.
for such more question on probability
https://brainly.com/question/13604758
#SPJ11
Related Questions
How many solutions exist for the given equation?
1/2(x+12) = 4x -1
zero
one
two
infinitely many
Answers
Answer:
one answer
x = 2
Step-by-step explanation:
Write the quotient and remainder when we divide (x^3 -4x^2 + 2x + 5) by (x - 2)

Answers
Answer:
Step-by-step explanation:
Sorry I can't explain how it is done. It is very difficult to explain on paper.

0123456 7 8 9 10 what is this called.........ence.fill in the missing space.
Answers
Answer:
sequence
Step-by-step explanation:
a sequence is essentially a set [group/list] of numbers, and each number has a specific placement [meaning that there is an order]
hope this helps!!
Answer: this, a set of number in an order, is called a sequence
fill in the blank: sequence
The area of a rectangular region is increasing at a rate of 20 square feet per hour. Which of the following is closest to this rate in square meters per minute? (Use 1 meter = 3.28 feet.)
A) 0.03
B) 0.10
C) 1.09
D) 2.03
Answers
0.03 is closest to this rate in square meters per minute. The correct option is option (A)
Given that the area of a rectangular region is increasing at a rate of 20 square feet per hour. find which of the following is closest to this rate in square meters per minute.
Using 1 meter = 3.28 feet.
1 square foot is equal to (1/3.28)² square meters. Therefore, 1 square foot = 0.0929 square meters. Rate of change of area = 20 square feet per hour.
Therefore, Rate of change of area in square meters per minute
= (20/60) x (0.0929)
= 0.0303 = 0.03 (rounded to two decimal places).Therefore, the option (A) 0.03 is the closest rate to the given rate of change of area in square meters per minute.
To learn more about area
https://brainly.com/question/25292087
#SPJ11
Finding the slope!
Help?

Answers
Answer:
Step-by-step explanation:
Slope is 0
Answer:The answer to the slope is 0.
The projected number of employed writers and authors in 2016 is 153,000. 12. 4% of those will have some college experience but no degree, and 84. 1% will have a bachelor’s degree or higher. If this holds true, how many more writers and authors with bachelor’s degree will there be than those with only some college experience and no degree?.
Answers
There are 109,761 more writers with a bachelor's degree or higher than those with only some college experience and no degree.
From the given data, Percent of writers with some college experience but no degree = 12.4%
Percent of writers with a bachelor's degree or higher = 84.1%The percentage of writers without any college experience can be found by:
Percent of writers without any college experience = 100% - (12.4% + 84.1%)
Percent of writers without any college experience = 3.5%T
Total number of writers with some college experience but no degree = 12.4% of 153,000= 18,972
Total number of writers with a bachelor's degree or higher = 84.1% of 153,000= 128,733
Total number of writers without any college experience = 3.5% of 153,000= 5,355
Therefore, the number of writers with a bachelor's degree or higher than those with only some college experience and no degree is:
128,733 - 18,972 = 109,761
Hence, there are 109,761 more writers with a bachelor's degree or higher than those with only some college experience and no degree.
Know more about Percent here:
https://brainly.com/question/24877689
#SPJ11
Determine the area of the regular polygon. (round to the nearest tenth)
13.3
16
Area = 5(apothem)(perimeter)
Answers
The area of the regular polygon is approximately 177.8 square units.
To find the area of a regular polygon, we can use the formula:
Area = ½(apothem)(perimeter)
We know that a regular polygon has all sides and angles equal. Therefore, we can use the formula for the perimeter of a regular polygon:
Perimeter = number of sides × length of a side
We can use the Pythagorean theorem to find the length of a side:
(length of a side/2)² + (apothem)² = (perpendicular distance from the center to a side)²
(length of a side/2)² + (13.3)² = (16)²
(length of a side/2)² = 256 - 176.89
length of a side/2 ≈ 7.92
length of a side ≈ 15.84
Now that we have the apothem and the perimeter, we can use the formula for the area of a regular polygon:
Area = ½(13.3)(15.84×5) ≈ 177.8
learn more about regular polygon here:
https://brainly.com/question/12518409
#SPJ1
Write a linear equation in the form y=mx+b that represents the table. x 0 1 2 3 4 y 15 13 11 9 7
Answers
Answer: A linear equation in the form y = mx + b can be determined by examining the values in the table. To find the value of m, we can use the formula for the slope of a line, which is (y2 - y1) / (x2 - x1). Using the first and last values in the table, we can compute the slope as (7 - 15) / (4 - 0) = -1/4.
Therefore, the equation that represents the table is:
y = (-1/4) * x + b
We can use any of the given points to find the value of b. For example, using the point (1, 13), we can solve the equation to find b:
13 = (-1/4) * 1 + b
b = 14 - 1/4 = 13 3/4
Therefore, the final equation that represents the table is:
y = (-1/4) * x + 13 3/4
Write the general form of the equation of the circle. Center: (−1,4); solution point: (2,1)
Answers
Answer:
r² = (2 - (-1))² + (1 - 4)² = 3² + (-3)² = 9 + 9 = 18
(x + 1)² + (y - 4)² = 18
The general form of the equation of the circle is `(x − h)² + (y − k)² = r²`, where the center of the circle is at `(h, k)` and the radius of the circle is `r`.
Given center: `(h, k) = (-1, 4)`Given solution point: `(x, y) = (2, 1)`Let the radius be `r`.
Then, using the distance formula, we can calculate the radius `r`.Distance between center and solution point is `r`i.e. `(x − h)² + (y − k)² = r²
Plugging in the values, we get:`(2 − (-1))² + (1 − 4)² = r²`
Solving for `r`, we get:`3² + (-3)² = r²`
⇒ 18 = r²
⇒ r = ±sqrt(18)`
The center of the circle is `(h, k) = (-1, 4)` and radius of the circle is `r = ±sqrt(18)`.
Hence, the equation of the circle in the general form is`(x − (-1))² + (y − 4)² = (±sqrt(18))²`
On simplifying, we get:`(x + 1)² + (y − 4)² = 18`Therefore, the required equation of the circle in the general form is `(x + 1)² + (y − 4)² = 18`.
Thus, the equation of the circle in the general form is `(x + 1)² + (y − 4)² = 18`.
To know more about distance formula, visit
https://brainly.com/question/32846365
#SPJ11
80MNP14. Suppose O is the midpoint of MQ and N is the midpoint of Mo. If NO = 8, find MQ.

Answers
MN+NO=MO
Where N is the midpoint of MO
Therefore:
MN = NO
MN = 8
NO = 8
8 + 8 = MO
MO = 16
Now:
MO + OQ = MQ
If O is the midpoint of MQ:
MO = OQ
OQ = 16
Therefore:
MQ = 16 + 16 = 32
A card is drawn from an ordinary deck and we are told that it is red. What is the probability that the card is greater than 2 but less than 92
Answers
The probability that the card is greater than 2 but less than 9 is 6 / 13.
Probability is the branch of discrete mathematics. It is used for calculating how likely an event is to occur or happen.
P ( E ) = Number of favourable outcomes / Total number of outcomes → 1
In an ordinary deck of cards,
Total number of cards = 52Number of suites = 4 ( Hearts, Clubs, Diamonds and spades )Each suite has 13 cards = Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack,Queen, King
Number of black suites = 13( Clubs ) + 13( Spades ) = 26Number of red suites = 13( Hearts ) + 13( Diamonds ) = 26As per the question,
A card is drawn from an ordinary deck and that is red.
⇒ Total number of red cards in an ordinary deck = 26 cards
∴ Total number of outcomes = 26
The card that is greater than 2 but less than 9,
⇒ Number of cards that are greater than 2 but less than 9 in red suite = 12
∴ Number of favourable outcomes = 12
Substitute the values in 1,
P ( E ) = Number of favourable outcomes / Total number of outcomes
= 12 /26
P ( E ) = 6 / 13
Therefore, 6 / 13 is the probability that the card is drawn in a red suite greater than 2 but less than 9.
To know more about Probability refer to:
https://brainly.com/question/25870256
#SPJ4
The complete question is
A card is drawn from an ordinary deck and we are told that it is red. What is the probability that the card is greater than 2 but less than 9?
A cyclist tide his a bike at a speed of 27 miles per hour. What is this speed in miles per minute? How many miles will the cyclist travel in 15 minutes? Do not round your answers
Answers
Answer:
0.45 miles per minute and 6.75
Step-by-step explanation:
27/60=0.45<-- Miles per minute
0.45x15=6.75<--Miles in 15 minutes
Hope this helps pls give brainliest
The flak are in the hape of cone. The maller flak ha a bae radiu of
8
cm and a vertical height of
20
cm. The larger flak ha a bae radiu of
14
cm. The larger flak i now partly filled with liquid up to a vertical height of
15
cm. Calculate the volume of liquid in the flak. Give your anwer in term of π
Answers
The volume of the liquid in the bigger flask which is in the shape of the cone is V = 980π.
What is a cone?
A cone is a recognizable three-dimensional geometric shape with a smooth and curving surface that is directed upward in mathematics. The
Greek word "konos," which denotes a peak or a wedge, is the source of the English word "cone."
The apex is the pointy end, while the base is the level area.
So, the volume of liquid in the bigger flask:
We know that the radius of the bigger flask is 14cm.
The liquid is filled to a height of 15cm.
The volume of cone formula: V = πr²h/3
Substitute values as follows:
V = πr²h/3
V = π(14)²15/3
V = π196*5
V = 980π
Therefore, the volume of the liquid in the bigger flask which is in the shape of the cone is V = 980π.
Know more about cones here:
https://brainly.com/question/1082469
#SPJ4
Given the system of equations below. Use the Inverse of the matrix method to solve. x+2y+3z=11
2x+4y+5z=21
3x+5y+6z=27
Answers
The solution of the given system of equations is x = -4, y = 5 and z = 2 is the answer.
The system of equations given below:x + 2y + 3z = 11;2x + 4y + 5z = 21;3x + 5y + 6z = 27.
Here, we will solve this system of equations using inverse of the matrix method as follows:
We can write the given system of equations in matrix form as AX = B where, A = [1 2 3; 2 4 5; 3 5 6], X = [x; y; z] and B = [11; 21; 27].
The inverse of matrix A is given by the formula: A-1 = (1/ det(A)) [d11 d12 d13; d21 d22 d23; d31 d32 d33] where,
d11 = A22A33 – A23A32 = (4 × 6) – (5 × 5) = -1,
d12 = -(A21A33 – A23A31) = -[ (2 × 6) – (5 × 3)] = 3,
d13 = A21A32 – A22A31 = (2 × 5) – (4 × 3) = -2,
d21 = -(A12A33 – A13A32) = -[(2 × 6) – (5 × 3)] = 3,
d22 = A11A33 – A13A31 = (1 × 6) – (3 × 3) = 0,
d23 = -(A11A32 – A12A31) = -[(1 × 5) – (2 × 3)] = 1,
d31 = A12A23 – A13A22 = (2 × 5) – (3 × 4) = -2,
d32 = -(A11A23 – A13A21) = -[(1 × 5) – (3 × 3)] = 4,
d33 = A11A22 – A12A21 = (1 × 4) – (2 × 2) = 0.
We have A-1 = (-1/1) [0 3 -2; 3 0 1; -2 1 0] = [0 -3 2; -3 0 -1; 2 -1 0]
Now, X = A-1 B = [0 -3 2; -3 0 -1; 2 -1 0] [11; 21; 27] = [-4; 5; 2]
Therefore, the solution of the given system of equations is x = -4, y = 5 and z = 2.
know more about matrix method
https://brainly.com/question/32106604
#SPJ11
Please help simplify and write your answer in the form a + bi

Answers
Answer:
\( 2 - 4i\)
Step-by-step explanation:
\( \frac{10}{1 + 2i} \\ \\ = \frac{10}{1 + 2i} \times \frac{1 - 2i}{1 - 2i} \\ \\ = \frac{10(1 - 2i)}{ {1}^{2} - {(2i)}^{2} } \\ \\ = \frac{10 - 20i}{ {1} - {4i}^{2} } \\ \\ = \frac{10 - 20i}{ {1} - {4( - 1)} } \\ ( \because \: {i}^{2} = - 1) \\ \\ = \frac{10 - 20i}{1 + 4} \\ \\ = \frac{5(2 - 4i)}{5} \\ \\ = 2 - 4i\)
Use method of reduction of order to find a second solution y2(x) of the homogeneuos equation and a particular solution of the given nonhomogeneous equation:
y" - 4y = 2; y1 = e^-2x
Please use equation and not substitution
Answers
The homogeneous equation and a particular solution of the given nonhomogeneous equation is \(& y=c_1 e^{-2 x}+c_2 e^{2 x}-\frac{1}{2}\).
The given nonhomogeneous equation is y" - 4y = 2
We are given \($y_1=e^{-2 x}$\)
Let \($y_2=u y_1$\)
A linear differential equation is homogeneous if it is a homogeneous linear equation in the unknown function and its derivatives.Non-homogeneous differential equations are simply differential equations that do not satisfy the conditions for homogeneous equations. In the past, we’ve learned that homogeneous equations are equations that have zero on the right-hand side of the equation.
The two most common methods when finding the particular solution of a non-homogeneous differential equation are:
The method of undetermined coefficients. The method of variation of parameters.\($$\begin{aligned}& y_2=u e^{-2 x} \\& y_2^{\prime}=u^{\prime} e^{-2 x}-2 u e^{-2 x} \\& y_2^{\prime \prime}=u^{\prime \prime} e^{-2 x}-2 u^{\prime} e^{-2 x}-2 u^{\prime} e^{-2 x}+4 u e^{-2 x} \\& y_2^{\prime \prime}=u^{\prime \prime} e^{-2 x}-4 u^{\prime} e^{-2 x}+4 u e^{-2 x}\end{aligned}$$\)
Substitute in \($y^{\prime \prime}-4 y=0$\), we get
\($$\begin{aligned}& u^{\prime \prime} e^{-2 x}-4 u^{\prime} e^{-2 x}+4 u e^{-2 x}-4 u e^{-2 x}=0 \\& u^{\prime \prime} e^{-2 x}-4 u^{\prime} e^{-2 x}=0 \\& e^{-2 x}\left(u^{\prime \prime}-4 u^{\prime}\right)=0 \\& u^{\prime \prime}-4 u^{\prime}=0 \\& u^{\prime \prime}=4 u^{\prime}\end{aligned}$$\)
Substitute \($$u^{\prime}=v$ and $u^{\prime \prime}=v^{\prime}$\), we get
\($$\begin{aligned}& v^{\prime}=4 v \\& \frac{d v}{d x}=4 v \\& \frac{1}{v} d v=4 d x\end{aligned}$$\)
Integrate both sides, we get
\($u=\frac{1}{4} C_1 e^{4 x}+C_2$$\)
put in \($y_2=u y_1$\)
\($$y_2=\left(\frac{1}{4} C_1 e^{4 x}+C_2\right) e^{-2 x}$$\)
Choose \($$C_1=4$ and $C_2=0$\), we get
\($$y_2=e^{2 x}$$\)
\($$\begin{aligned}& y_c=c_1 y_1+c_2 y_2 \\& y_c=c_1 e^{-2 x}+c_2 e^{2 x}\end{aligned}$$\)
Particular Solution
\($$\begin{aligned}& y_y=A \\& y_y{ }^{\prime}=0 \\& y_y{ }^{\prime \prime}=0\end{aligned}$$\)
Substitute in \($y^{\prime \prime}-4 y=2$\), we get
\($$\begin{aligned}& 0-4 A=2 \\& -4 A=2 \\& A=-\frac{1}{2} \\& \therefore y_y=-\frac{1}{2}\end{aligned}$$\)
General Solution
\($$\begin{aligned}& y=y_6+y_y \\& y=c_1 e^{-2 x}+c_2 e^{2 x}-\frac{1}{2}\end{aligned}$$\)
Therefore, the second equation is \(& y_{2} =c_1 e^{-2 x}+c_2 e^{2 x}-\frac{1}{2}\).
For more such questions on homogeneous & nonhomogeneous equation
https://brainly.com/question/15839620
#SPJ4
find the area and the perimeter of the landing area of the pole vault pit shown to the right
Answers
we have that
the landing area is a square
so
the area of a square is
A=b^2
and the perimeter is equal to
P=4b
we have
b=16.5 ft
A=16.5^2=272.25 ft2
P=16.5(4)=66 ft
Rodarius wants to make a special for the raffle. He has 120 mini footballs and 30 autographs from the titans. What is the most amount of gift packages he can make so that each recipient gets an equal number of footballs and auto graphs?
Answers
Step-by-step explanation:
robarius wants to make a special gift for raffle.he has 120 mini footballs and 30 signed autographs from the titans. what is the most amount of gift packages he can make so that each recipient gets an equal number of footballs and autographsA die with sides numbered 1 to 6 is rolled. Find the probability of rolling each outcome.
P(5)=
P(1 or 2)=
P(odd number)=
P(not 6)=
P(even number)=
P(1,2,3, or 4)=
PLEASE HELP IM LIKE IN A RUSHHH TYSM IF U ANSWER QUICKLY
Answers
Step-by-step explanation:
Probability is the ratio of number of success/ total outcomes
So let calculate each probability
We have six total outcomes here in each scenario.
P(5)=1/6
P(1 or 2)=2/6=1/3
P(odd number )=3/6=1/2
P(not 6)= 5/6
Also
P(not 6)=1-P(6)=5/6
P(even number)=3/6=1/2
P(1,2,3,4)=4/6=2/3
P(5) = 1/6 (since there is only one side with the number 5, and there are six equally likely outcomes)
P(1 or 2) = P(1) + P(2) = 1/6 + 1/6 = 2/6 = 1/3 (since there are two sides with the numbers 1 and 2)
P(odd number) = P(1) + P(3) + P(5) = 1/6 + 1/6 + 1/6 = 3/6 = 1/2 (since there are three odd numbers: 1, 3, and 5)
P(not 6) = 1 - P(6) = 1 - 1/6 = 5/6 (since there are five sides that are not 6)
P(even number) = 1 - P(odd number) = 1 - 1/2 = 1/2 (since there are three odd numbers and three even numbers)
P(1, 2, 3, or 4) = P(1) + P(2) + P(3) + P(4) = 1/6 + 1/6 + 1/6 + 1/6 = 4/6 = 2/3 (since there are four sides with the numbers 1, 2, 3, and 4)
I hope this helps! Let me know if you have any further questions.
The groundkeep filled the first sandbox with sand to a height of 6 inches what is the volume in cubic feet of the sand that was used to kill the first sandbox to a night of 6inches
Answers
Answer:
https://nrckids.org/CFOC/Infant_Toddlers
Step-by-step explanation:
a large emerald with a mass of 982.7 grams was recently discovered in a mine. if the density of the emerald is 2.76, what is the volume? round to the nearest hundredth when necessary, and only enter numerical values, which can include a decimal point. answer for blank 1:
Answers
The volume of the large emerald with a mass of 982.7 grams and a density of 2.76 is approximately 355.62 cubic centimeters.
Density is defined as the mass per unit volume. To find the volume, we can use the formula:
Density = Mass / Volume
Rearranging the formula, we get:
Volume = Mass / Density
Substituting the given values, we have:
Volume = 982.7 grams / 2.76
Calculating this, we find:
Volume ≈ 355.62 cubic centimeters
Therefore, the volume of the large emerald is approximately 355.62 cubic centimeters.
This means that if the emerald is shaped like a perfect cube, each side would measure approximately 7.07 centimeters (since the volume of a cube is given by side^3).
Learn more about Density click here :brainly.com/question/6838128
#SPJ11
Please help I’ll give you guys brainiest!:)

Answers
Answer: below
Domain: (0,1,2)
Range: (15,18,21)
Step-by-step explanation: Domain is possible input values while range is possible output values. So if it is for 0 minutes it will be 15 degrees, 1 minute 18 degrees because 15 + 3( 0 or 1 or 2 etc.). And for 2 minutes it would be 21 degrees. This could go on forever in a graph but I picked 3 simple points, 0, 1, and 2 minutes.
Hope this helps!
create a real world problem involving a related set of two equations
Answers
The real-world problem involving a related set of two equations is given below:
Problem: Cost of attending a concert is made up of base price and variable price per ticket. You are planning to attend a concert with your friends and want to know the number of tickets to purchase for lowest overall cost.
What are the two equations?The related set of two equations are:
Equation 1: The total cost (C) of attending the concert is given by:
The equation C = B + P x N,
where:
B = the base price
P = the price per ticket,
N = the number of tickets purchased.
Equation 2: The maximum budget (M) a person have for attending the concert is:
The equation M = B + P*X
where:
X = the maximum number of tickets a person can afford.
So by using the values of B, P, and M, you can be able to find the optimal value of N that minimizes the cost C while staying within your own budget M. so, you can now determine ticket amount to minimize costs and stay within budget.
Learn more about equations from
https://brainly.com/question/2972832
#SPJ1
What is the value of x in the triangle?

Answers
Answer: \(D. 6\sqrt{x} 2\) is the answer
Step-by-step explanation:
What is the number that makes the ratio equivalent to 3:6?
Answers
Answer:
I think 3/6
Step-by-step explanation:
3:6=3/6
Robert has a dog that weights 4 times as much as fiona’s dog. The total weight of the dogs is 75 pounds. How much does fiona’s dog weigh
Answers
Explanation you divide 75 by 4
Can SOMEONE PLEASE HELP ME I NEED HELP!!! Please I don’t get it!!!

Answers
Step-by-step explanation:
Hint :- FH is total length of the line. And FG is the length of the line till point G. We need tos subtract the total length and Length of FG
GH = FH - FG
GH = 15 - 9.7
GH = 5.3 cm
Answer:
GH = 5.3 mm
Step-by-step explanation:
the full length of the line is 15 mm
and FG = 9.7 mm Then GH= 15 - FG
= 15- 9.7 = 5.3
you can think of it like a rope with 15 mm length if you cut ✂️ 9.7 mm u will have 5.3 left
Match the stem and leaf plot
to the correct set of data.
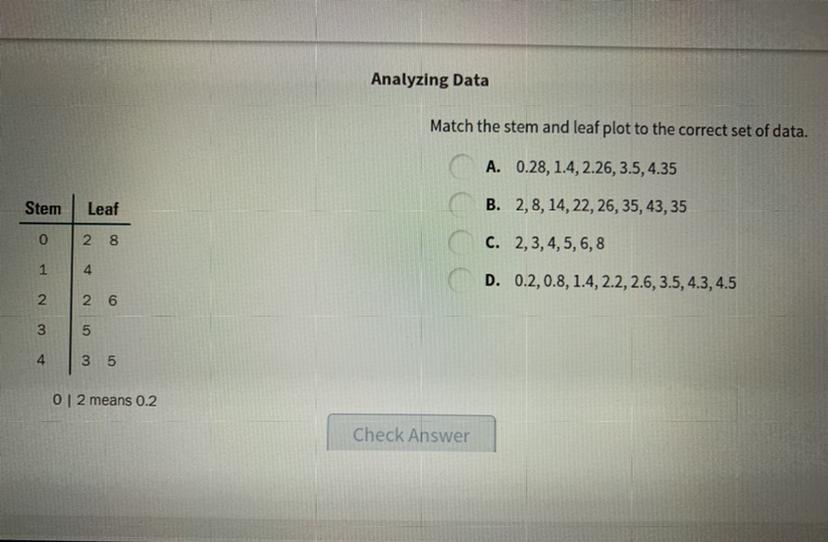
Answers
In the equation (x - 7)^2 = 25, if x equals 12, is there another solution for x?
(It's confusing but it means is there any other possible answer for x except 12.)
Answers
Answerh
Step-by-step explanation:
huh
I really need some help with this

Answers
Answer:
4
Step-by-step explanation:
The average rate of change of f(x) in the closed interval [ a, b ] is
\(\frac{f(b)-f(a)}{b-a}\)
Here [ a, b ] = [ 0, 4 ] , thus
f(b) = f(4) = - 4² + 8(4) - 4 = - 16 + 32 - 4 = 12
f(a) = f(0) = - 4 , then
average rate of change = \(\frac{12-(-4)}{4-0}\) = \(\frac{12+4}{4}\) = \(\frac{16}{4}\) = 4