Can you give a detailed example of a specific scenario, outside of pure math, where eigenvectors are useful? I know about lots of general applications (image processing, differential equations, etc) but I want something specific.
No answer take the points.
Answers
Answer:
Thx
Step-by-step explanation:
Image processing
Related Questions
The Freeman family is barbecuing veggie burgers, corn cobs, and mushroom caps in their local park. If 3 8 of the items barbecued are veggie burgers, and 1 3 of the items barbecued are corn cobs, what fraction of barbecued items are mushroom caps?
Answers
Answer:
The answer is below
Step-by-step explanation:
The Freeman family barbecued veggie burgers, corn cobs, and mushroom caps. 3/8 of the items barbecued are veggie burgers, and 1/3 of the items barbecued are corn cobs.
Let the total number of berbecued items be x. Therefore:
x = barbecued veggie burgers + barbecued corn cobs + barbecued mushroom caps
Barbecued veggie burgers = (3/8)x, barbecued corn cobs = (1/3)x, Let barbecued mushroom caps be y
Substituting:
x = (3/8)x + (1/3)x + y
Multiply through by 24
24x = 9x + 8x + 24y
24x = 17x + 24y
24y = 24x - 17x
24y = 7x
y = (7/24)x
barbecued mushroom caps = (7/24) of items
7/24 of the items barbecued are mushroom caps
Using fractions, it is found that the fraction of barbecued items that are mushroom caps is of \(\frac{7}{24}\).
---------------------------
The total proportion of all products is 100% = 1.The fraction corresponding to veggie burgers is \(\frac{3}{8}\).The fraction corresponding to corn cobs is \(\frac{1}{3}\).The fraction corresponding to mushroom caps is x.---------------------------
Thus:
\(\frac{3}{8} + \frac{1}{3} + x = 1\)
Solving for x, we find the fraction of mushroom caps.The least common multiple of 3 and 8 is 24.Then:
\(\frac{3\times3 + 8\times1 + 24x}{24} = 1\)
\(\frac{17 + 24x}{24} = 1\)
\(17 + 24x = 24\)
\(24x = 7\)
\(x = \frac{7}{24}\)
The fraction of barbecued items that are mushroom caps is of \(\frac{7}{24}\).
A similar problem is given at https://brainly.com/question/4231000
A line segment with endpoints P(1, 2) and Q (4,3) Is reflected across the line y=x. What are the new coordinates of the endpoints of the line segment?
Answers
Reflection across the line y=x transforms the point (x, y) into (y, x). Then,
P(1, 2) → P'(2, 1)
Q(4,3) → Q'(3, 4)
The new coordinates are P'(2, 1) and Q'(3, 4)
10
The Carvers' basement has the dimensions shown below.
The family plans to have wall-to-wall carpeting installed.
How many square feet of carpeting will the family need?
Show your work.
22 ft
56 ft
48 ft
10 ft
Answers
The area of the rectangular basement carpeting carvers' family need is :Area = 56 sq. ft.
Explain about the rectangle?An object with a rectangle's four sides, four corners, and four right angles is a 2D shape. In a rectangle, the opposite sides are equal in length, with one pair substantially longer compared to the opposite pair.
An equiangular quadrilateral is another name for a rectangle. The reason for this is that a rectangle is now a quadrilateral form (4-sided shape) with parallel sides that are equal to one another and four corners with 90o angles.
A rectangle can also be referred to as an equiangular quadrilateral because all of the angles are 90 degrees.
The given dimensions of the rectangular carvers' basement:
length 8 ft and width 7 ft.
Area = length x width
Area = 8 ft x 7 ft.
Area = 56 sq. ft.
Thus, the area of the rectangular basement carpeting carvers' family need is :Area = 56 sq. ft.
Know more about the rectangle
https://brainly.com/question/25292087
#SPJ1
The complete questions:
The Carvers' basement has the dimensions shown below.
The family plans to have wall-to-wall carpeting installed.
Dimension: length 8 ft and width 7 ft.
How many square feet of carpeting will the family need?
Show your work.
22 ft²
56 ft²
48 ft²
10 ft²
Find the perioa
equation.
llowing
y = 2 cos(5x + 3) - 6
77
Period = [2]T
Give your answer in simplest form.
![Find the perioaequation.llowingy = 2 cos(5x + 3) - 677Period = [2]TGive your answer in simplest form.](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/LQPTncYwbgWAlBk9oUI1EamQ5J0oFRZg.png)
Answers
Answer:
In the equation y = 2 cos(5x + 3) - 6, we can ignore the coefficients 2 and -6 for the purposes of calculating the period because they do not change the period. They only change the amplitude (2) and vertical shift (-6) of the function.
The coefficient 5 in front of x inside the cosine function affects the period of the function. It is a horizontal compression/stretch of the graph of the function.
The period of the basic cosine function, y = cos(x), is 2π. When there is a coefficient (let's call it b) in front of x, such as y = cos(bx), the period becomes 2π/b.
So, in your case, b = 5, so the period T of the function y = 2 cos(5x + 3) - 6 is:
T = 2π / 5
This is the simplest form for the period of the given function.
The increased availability of light materials with high strength has revolutionized the design and manufacture of golf clubs, particularly drivers. One measure of drivers that result in much longer tee shots is known as the coefficient of restitution of the club. An experiment was performed in which 15 drivers produced by a particular club maker were selected at random and their coefficients of restitution measured. It is of interest to determine if there is evidence to support a claim that the mean coefficient of restitution exceeds 0.82. Assume values to be normally distributed. The following observations were obtained for the 15 drivers:
0.8411 0.8191 0.8182 0.8125 0.8750
0.8580 0.8532 0.8483 0.8272 0.7983
0.8042 0.8730 0.8282 0.8359 0.8660
Conduct the test using a significance level of 0.05.
Answers
Answer:
WE reject the Null and conclude that the mean coefficient of restitution exceeds 0.82
Step-by-step explanation:
This is a one sample t test :
The hypothesis :
H0 : μ = 0.82
H0 : μ > 0.82
Given the sample data:
0.8411 0.8191 0.8182 0.8125 0.8750
0.8580 0.8532 0.8483 0.8272 0.7983
0.8042 0.8730 0.8282 0.8359 0.8660
Sample size, n = 15
Sample mean = ΣX / n = 0.837
Sample standard deviation, s = 0.0246 (from calculator)
The test statistic :
T = (xbar - μ) ÷ (s/√(n))
T = (0.837 - 0.82) ÷ (0.0246/√(15))
T = 2.676
The critical value at α = 0.05
df = n - 1 ; 15 - 1 = 14
Tcritical(0.05, 14) = 1.761
Reject H0 if Test statistic > Tcritical
Since, 2.676 > 1.761 ; WE reject the Null and conclude that the mean coefficient of restitution exceeds 0.82
write an equation for the graph

Answers
Answer:
y = 2x - 3.
Step-by-step explanation:
The slope is 2 and the y-intercept is at y = -3
Solve the equation: 7(8 - 5z) + 17 = 3
Answers
Answer:
z=2
Step-by-step explanation:
56-35z+17=3
73-35z=3
-35z=-70
z=2
2) f(x) = x2 - 6x +11
Degree:
Lead Coefficient:
End behavior:
Answers
Answer:
13 - 6 x
Step-by-step explanation:
Rewrite the polynomial 2x2 + x + +-7x + 1 in standard form.
Answers
Answer:
x-7x+5
Step-by-step explanation:
4+x-7x+1
x-7x+5
Help ASAP!!!! Plsssss
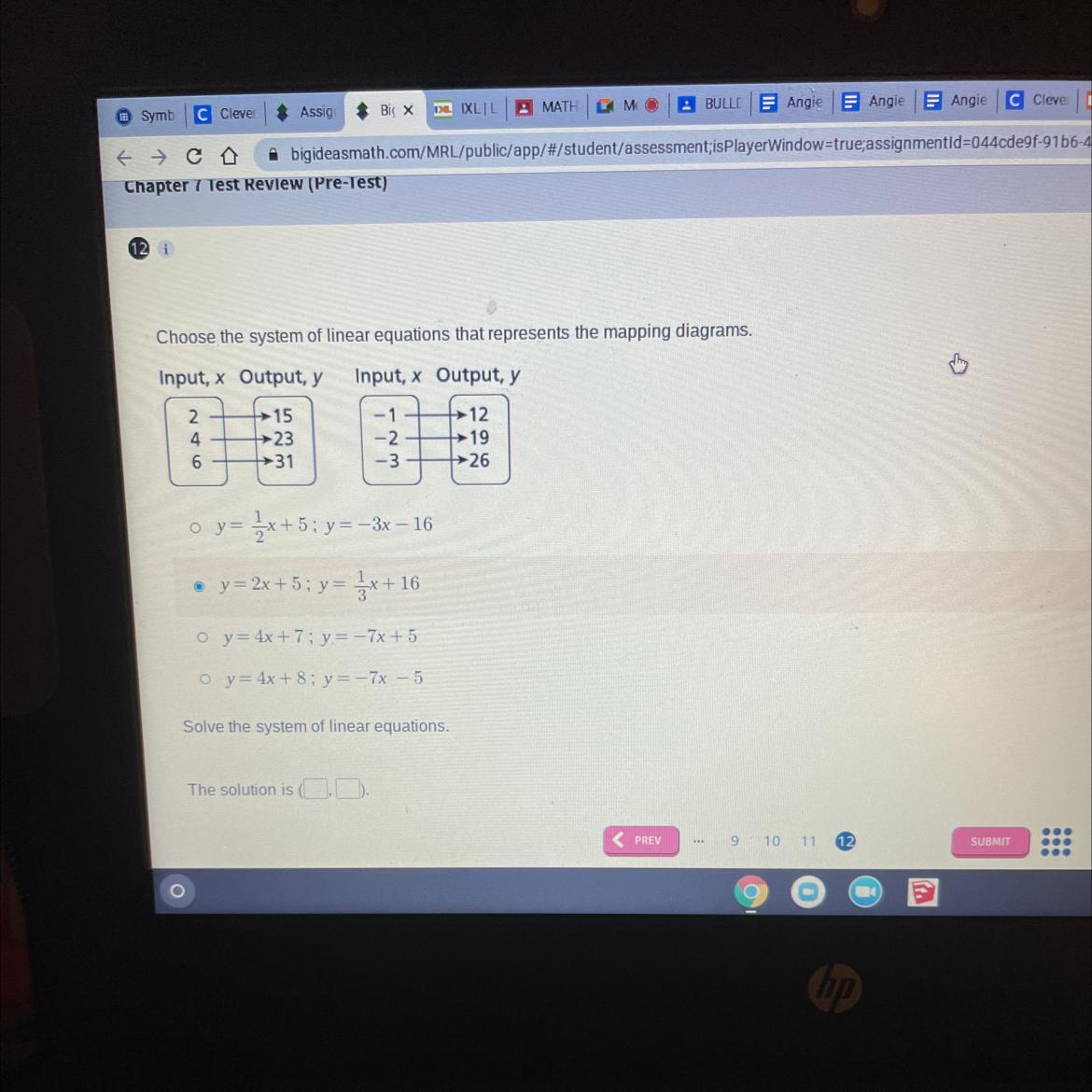
Answers
Answer:
2. y = 4x+7; y=-7x+5
Step-by-step explanation:
Please answer these 3 questions

Answers
The Volume of the box is 12 cubic unit.
We have,
Height = 1 unit
Width = 2 unit
Length = 6 unit
So, Volume of box
= l w h
= 1 x 2 x 6
= 12 cubic unit
Learn more about Volume here:
https://brainly.com/question/13338592
#SPJ1
What does AxB equal in I-ready Math?
Answers
Un terreno tiene 205 metros y cada metro cuesta 315 cuánto vale el terreno
Answers
Answer:
64,765
Step-by-step explanation:
multiplicas porque dice que uno cuesta 315 entonces si hay 205 hay 64,765
The volume V, of a cylinder is V=pie times radius to the power of 2 h, where r is the radius of the cylinder and h is the height. Using rounding to the nearest whole number, which of the following is an estimate of the volume of a cylinder with a radius of 3.75 inches and height of 6.21 inches
Answers
Answer:
\(274\,\text{in}^3\)
Step-by-step explanation:
\(V=\pi r^2h=\pi(3.75)^2(6.21)\approx274\,\text{in}^3\)
A customer will get gallons for 3.50
Answers
Answer:
What is the question?
Step-by-step explanation:
If its how much will it cost to get ____ gallons
Just multiply the number of gallons you want and 3.50 (the price)
Again, I don't really know what your question is, but I'm saying this so that if what I put up there is actually what your question was, you don't have to make another one. (I'm not sure if you can edit questions or not.)
PLEASE HELP ITS DUE TODAYYYYYY

Answers
Answer:
80 degrees
Step-by-step explanation:
Divide.
−10 ÷ −2
Drag and drop the correct number into the box to complete the sentence.

Answers
Line segment EF had endpoints E(5,-1) and F(-3,8). What are the coordinates of the midpoint of EF?
Answers
Answer:
(1, 7/2)
Step-by-step explanation:
the formula for midpoint is \((\frac{X1 + X2}{2}\), \(\frac{Y1 + Y2}{2})\)
Shawn has 25 coins, all nickels and dimes. The total value is $2.00. How many of each coin does he have ?
Answers
Answer:
\(\boxed{15 \ dime \ and \ 10 \ nickel \ coins}\)
Step-by-step explanation:
1 dime = 10 cents
1 nickel = 5 cents
So,
If there are 15 dimes
=> 15 dimes = 15*10 cents
=> 15 dimes = 150 cents
=> 15 dimes = $1.5
Rest is $0.5
So, for $0.5 we have 10 nickels coins
=> 10 nickels = 10*5
=> 10 nickels = 50 cents
=> 10 nickel coins = $0.5
Together it makes $2.00
3x-3+6 how many solutions would the equation have explain
Answers
Answer: 3x + 3
Step-by-step explanation:
The height of a cone is twice the radius of its base.
What expression represents the volume of the cone, in
cubic units?
2/3лх^3
4/3лх^3
2лх^3
4лх^3
Answers
Answer: 2/3πx³
Step-by-step explanation:
Let the radius of the cone be represented by x.
Since the height of the cone is twice the radius of its base, the height will be: = 2x
Volume of a cone = 1/3πr²h
where,
r = x
h = 2x
Volume of a cone = 1/3πr²h
= 1/3 × π × x² × 2x
= 1/3 × π × x² × 2x
= 1/3 × π × 2x³
= 2/3πx³
Therefore, the correct answer is 2/3πx³.
What is the perimeter, in units, of ΔABC Δ A B C with A(−1,−6) A B(7,−6), and C(3,−3)
Answers
Answer:
the perimeter in unites of abc with 3, -3 is a
Answer:
18 Units
Step-by-step explanation:
According to the calculator
Determine the number of non-negative integers M that satisfy exactly three of the four statements below.(1) M is prime(2) M + 3 is prime(3) 1 < √ < 8(4) M + 5 has an odd number of factors
Answers
SOLUTION
A non-negative integer is either positive or zero. It's the union of the natural numbers and the number zero.
A prime number is a number with only two factors, which are 1 and the number itself
Let consider the number
\(2\)1) It satisfies the first statement
M is prime
2 is prime
2) M+3 is prime
since
\(\begin{gathered} m=2 \\ 2+3=5\text{ } \\ 5\text{ is prime } \end{gathered}\)Hence
The second statement is satisfied
The third statement says
\(\begin{gathered} 1<\sqrt[]{m}<8 \\ \text{which is } \\ 1<\sqrt[]{2}<8 \end{gathered}\)\(\begin{gathered} \text{ since } \\ \sqrt[]{2}=1.414\ldots \\ \text{the third statement is satisfied } \end{gathered}\)Hence the third statement is satisfied
M=2
Since exactly 3 of the 4 statements is satisfied
From the second condition,
\(M+3\text{ is prime }\)All prime numbers except 2 are odd numbers
Also,
The sum of two odds is even
\(\text{let n be the prime numbers satisfying all the given conditions above }\)from the second condition,
M+3 is prime
\(\begin{gathered} n+3\text{ is even } \\ \text{which contradicts the second conditions } \end{gathered}\)Hence
There is no other prime number that satisfies exactly three of the four conditions above
Therefore,
The number of non-negative integers that satisfy exactly three of the four conditions is 1
There is only one non-negative integer M which is 2 that satisfy the condition 1,2,3 above
Ques
on 4 OT 5
The graph below is the graph of a function.
5
O A. True
ОО
OB. False
SUBMIT

Answers
What is the area of a triangle with a base of 8 and a height of 16?
Answers
Answer:
\( \frac{1}{2} \times 8 \times 16 \\ = 64\)
The answer you are looking for is 64 m².
Solution/Explanation:
First, setting up the formula for the area of a triangle,
A=1/2bh
Next, substituting the given values of the base and the height,
A=1/2(8)(16)
Now, simplifying it to get to the final answer,
A=64 m²
So, therefore, the final answer is 64 m².
I hope this helped you find your answer. Enjoy your day, and take care!
Find all solutions of each equation on the interval 0≤ x <2pie
tan² x sec² x +2 sec²x - tan²x =2
Answers
The trigonometric equations has the following solutions: x = 0 + j · π or x = 0.352π + j · π or x = - 0.352π + j · π, where j is a non-negative whole number.
How to solve a trigonometric equation
In this problem we find the case of a trigonometric equation, whose solutions on the interval [0, 2π] must be found. This can be done by both algebra properties and trigonometric formulae. First, write the entire expression:
tan² x · sec² x + 2 · sec² x - tan² x = 2
Second, use trigonometric formulas to reduce the number of trigonometric functions:
tan² x · (tan² x + 1) + 2 · (tan² x + 1) - tan² x = 2
Third, expand the equation:
tan⁴ x + tan² x + 2 · tan² x + 2 - tan² x = 2
tan⁴ x + 2 · tan² x = 0
Fourth, factor the expression:
tan² x · (tan² x - 2) = 0
tan² x = 0 or tan² x = 2
tan x = 0 or tan x = ± √2
Fifth, determine the solutions to trigonometric equation:
x = 0 + j · π or x = 0.352π + j · π or x = - 0.352π + j · π, where j is a non-negative whole number.
To learn more on trigonometric equations: https://brainly.com/question/22624805
#SPJ1
It’s takes an aero plane 3.2 hours to fly from Mumbai to Seoul. It takes the same aero plane 1 1/3 hours to fly from Seoul to Tokyo. How many hours does it take the aero plane to travel from Mumbai to Tokyo if it flies through Seoul?
Answers
To find the total time it takes for the airplane to travel from Mumbai to Tokyo via Seoul, we need to add the time taken for the Mumbai-Seoul leg and the Seoul-Tokyo leg.
The airplane takes 3.2 hours to fly from Mumbai to Seoul.
The airplane takes 1 1/3 hours to fly from Seoul to Tokyo, which is equivalent to 1.33 hours.
To find the total time, we add the two durations:
3.2 hours + 1.33 hours = 4.53 hours
Therefore, it takes approximately 4.53 hours for the airplane to travel from Mumbai to Tokyo if it flies through Seoul.
Identify the function's local and absolute extreme values, if any, saying where they occur. f(x) = x^3 + 4x^2 - 3x - 4 A) local maximum at x = -1/3; local minimum at x = 3 B) local maximum at x = -1; local minimum at x = 1 C) local maximum at x = -3; local minimum at x 1/3 D) local maximum at x = -1; local minimum at x = 1
Answers
Answer: C) local maximum at x = -3; local minimum at x = 1/3
Step-by-step explanation:
Given the function:
f(x) = x^3 + 4x^2 - 3x - 4
Set f'(x) = 0
f'(x) = 3x² + 8x - 3
f'(x) = 0
3x² + 8x - 3 = 0
Using the quadratic function calculator :
x = - 3 or x = 1/3
Critical points = - 3 ; 1/3
To find the maximum and minimum points :
f''(x) = 6x + 8
Substitute the values of X in
At x = - 3
6(-3) + 8
-18 + 8 = - 10
At x = 1/3
6(1/3) + 8
2 + 8 = 10
Value of f''(x) at - 3 is negative, hence - 3 is the maximum point
Value of f''(x) at 1/3 is positive , hence 1/3 is the minimum point
Cos5pi/3 =
A. 3/2
B.1/2
C. 2/2
D.-2/2
HELPP
Answers
Answer:
B) 1/2
Step-by-step explanation:
Note that pi=180.
Then we have 180/3=60 and so 5*60=300.
Thus cos 300=1/2.
Therefore, cos 5pi/3=1/2.
Answer: B
Step-by-step explanation:
Which expression is equivalent to StartRoot 8 x Superscript 7 Baseline y Superscript 8 Baseline EndRoot? Assume x greater-than-or-equal-to 0.
x y squared StartRoot 8 x cubed EndRoot
2 x cubed y cubed StartRoot x y squared EndRoot
2 x cubed y Superscript 4 Baseline StartRoot 2 x EndRoot
4 x cubed y Superscript 4 Baseline StartRoot x EndRoot
Answers
The expression that is equivalent to StartRoot \(8 x^7 y^8\) EndRoot is (\(2 x^3 y^4\) StartRoot 2 x EndRoot)^2.
To understand why this is the case, let's break down each expression and simplify them step by step:
StartRoot \(8 x^7 y^8\) EndRoot:
We can rewrite 8 as \(2^3\), and since the square root can be split over multiplication, we have StartRoot \((2^3) x^7 y^8\) EndRoot. Applying the exponent rule for square roots, we get StartRoot \(2^3\) EndRoot StartRoot \(x^7\) EndRoot StartRoot \(y^8\) EndRoot.
Simplifying further, we have 2 StartRoot \(2 x^3 y^4\) EndRoot StartRoot \(2^2\) EndRoot StartRoot \(x^2\) EndRoot StartRoot \(y^4\) EndRoot. Finally, we obtain 2 \(x^3 y^4\) StartRoot 2 x EndRoot, which is the expression in question.
(\(2 x y^2\) StartRoot 8 x^3 EndRoot)^2:
Expanding the expression inside the parentheses, we have \(2 x y^2\)StartRoot \((2^3) x^3\) EndRoot. Applying the exponent rule for square roots, we get \(2 x y^2\) StartRoot \(2^3\) EndRoot StartRoot \(x^3\) EndRoot.
Simplifying further, we have \(2 x y^2\) StartRoot 2 x EndRoot. Squaring the entire expression, we obtain (\(2 x y^2\) StartRoot 2 x EndRoot)^2.
Therefore, the expression (\(2 x^3 y^4\) StartRoot 2 x EndRoot)^2 is equivalent to StartRoot \(8 x^7 y^8\) EndRoot.
For more such questions on expression
https://brainly.com/question/1859113
#SPJ8