Answers
Answer:
the correct answer is the last one.
Step-by-step explanation:
good luck on ur test :)
Answer:
0.27
-0.07
0.20
Step-by-step explanation:
A
If it is not A it is a trick question, or a mistake
Report the problem if you can.
Related Questions
The local rat population numbers approximately 250 and is increasing at a rate of 9% per year
Answers
The approximate rat population after a year is 272.5. It means the population will increase from 250 to 272.5
The local rat population numbers approximately 250 and is increasing at a rate of 9% per year.
We need to calculate the approximate rate population after a year.
The formula to calculate the growth rate of a population is given by: N(t) = N0 × (1 + r)^t
Where,N0 is the initial population of the organism.
N(t) is the population after time, t.r is the rate of growth (positive or negative).
t is the time in years.
Applying the above formula to calculate the approximate rat population after a year:
N(1) = 250 × (1 + 9/100)^1N(1) = 250 × 1.09N(1)
= 272.5
Therefore, the approximate rat population after a year is 272.5.
It means the population will increase from 250 to 272.5,
learn more about population from given link
https://brainly.com/question/29885712
#SPJ11
how do i write this equation in function notation.
=−2/5+1
Answers
Answer:
f(x) = −2/5x + 1
Step-by-step explanation:
when putting an equation in function notation first you must make sure the equation is in slope-intercept form and then you must rewrite the equation but instead of putting y you will replace it with f(x), or g(x), whichever one you are given directions to put it as.
Hope This Helps!
Plz Mark Brainliest!
Is 3.1 terminating or repeating
Answers
Answer:
Depends if there is a line above the "1".
Step-by-step explanation:
If it were the attached image it would be repeating>>
If not and it's just 3.1, its terminal.
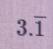
Bill and Ashley decided to see who could collect more rocks. The relation is given by the inequality a > 3b + 6. If Bill collected 20 rocks, what is the least number of rocks Ashley collected?
Answers
If Bill collected 20 rocks and the inequality a > 3b + 6 holds true, the least number of rocks Ashley collected can be determined by substituting the value of a and solving for b. The answer is found to be 5 rocks.
Given the inequality a > 3b + 6, where a represents the number of rocks collected by Bill and b represents the number of rocks collected by Ashley, we need to find the least possible value of b. Since Bill collected 20 rocks, we can substitute a = 20 into the inequality: 20 > 3b + 6.
By simplifying the inequality, we get 14 > 3b. Dividing both sides by 3, we find that b must be less than 4.66. However, b represents the number of rocks collected, so it must be a whole number. Therefore, the least number of rocks Ashley collected is 5.
To learn more about inequality click here: brainly.com/question/20383699
#SPJ11
determine which function has the greater rate of change in problems 1−3
1.
x y
-------
-1 0
0 1
1 2
2 3
(1 point)
The rates of change are equal.
The graph has a greater rate of change
The table has a greater rate of change.
none of the above
2. y = 2x + 7
The slopes are equal.
The graph has a greater slope.
The equation has a greater slope.
none of the abov
3. As x increases by 1, y increases by 3
The slopes are equal.
The graph has a greater slope.
The function rule has a greater slope.
none of the above
Answers
The table has a greater rate of change.
The rates of change are equal.
In the given problem, we have a table showing the relationship between x and y values. By comparing the change in y with the change in x, we can determine the rate of change. Looking at the table, we observe that for every increase of 1 in x, there is a corresponding increase of 1 in y. Therefore, the rate of change for this table is 1.
The slopes are equal.
The equation has a greater slope.
In problem 2, we are given a linear equation in the form y = mx + b, where m represents the slope. The given equation is y = 2x + 7, which means the slope is 2. To compare the rates of change, we compare the slopes. If the slopes are equal, the rates of change are equal. In this case, the slopes are equal to 2, so the rates of change are the same.
The function rule has a greater slope.
The slopes are equal.
In problem 3, we are told that as x increases by 1, y increases by 3. This information gives us the rate of change between x and y. The slope of a function represents the rate of change, and in this case, the slope is 3. Comparing the slopes, we find that they are equal, as both have a value of 3. Therefore, the rates of change are the same.
Similar question here:
https://brainly.com/question/29181688?referrer=searchResults
#SPJ11
4x - 9y = 1
2x + y = -5
Answers
Answer:
y=1
x=5/2
Step-by-step explanation:
4x-9y=1
(2x+y=-5)-2
4x-9y=1
-4x-2y=10
_________
-11y=11
y=-1
4x-9y=1
4x-9(1)=1
4x=10
x=10/4
x=5/2
Juan compró un terreno rectangular cuyo perímetro es de 88 m. Se sabe que la medida de lo largo del terreno es 2veces la medida de su ancho más 2 metros ¿cuáles son las medidas del terreno que compro Juan ? ¿Cual es el ares del terreno de Juan ?
Answers
Answer:
420 m^2
Step-by-step explanation:
Ancho: x
Largo: 2x + 2
2x + 2(2x+2) = 88
2x + 4x + 4 = 88
6x = 88 - 4
x = 84/6
x = 14
Ancho: 14
Largo : 30
Area: 14 * 30 = 420 metros cuadrados
a gardener has 322 tulip bulbs she wants to plant rows of 15 bulbs how many bulbs can be planted how many bulbs will she have left over
Answers
Answer:315 bulbs planted and 7 left over
Step-by-step explanation:322/15 = 21.44
Roughly around 21 rows.
21 x 15 = 315 bulbs planted
322 - 315 = 7 bulbs left over
Let F(x) be an antiderivative of (ln x)^3/x. If F(1) = 0, then F(9) =
a. .048
b. .144
c. 5.827
d. 23. 308
e. 1,640.250
Answers
the value of F(9) is approximately 23.308.
To find the value of F(9) given that F(x) is an antiderivative of (ln x)^3/x and F(1) = 0, we can use the fundamental theorem of calculus.
According to the fundamental theorem of calculus, if F(x) is an antiderivative of a function f(x), then:
∫[a,b] f(x) dx = F(b) - F(a)
Since F(1) = 0, we can write:
∫[1,9] (ln x)^3/x dx = F(9) - F(1)
To evaluate the integral, we can make a substitution:
Let u = ln x, then du = (1/x) dx
The integral becomes:
∫[ln 1, ln 9] u^3 du
Integrating u^3 with respect to u:
[(1/4)u^4] | [ln 1, ln 9] = (1/4)(ln 9)^4 - (1/4)(ln 1)^4
Since ln 1 = 0, we have:
(1/4)(ln 9)^4 - (1/4)(ln 1)^4 = (1/4)(ln 9)^4
Therefore, F(9) - F(1) = (1/4)(ln 9)^4
Since F(1) = 0, we can conclude that F(9) = (1/4)(ln 9)^4.
Calculating this value:
F(9) = (1/4)(ln 9)^4 ≈ 23.308
to know more about calculus visit:
brainly.com/question/29097043
#SPJ11
a car tire has a radius of 10.4 inches what distance will the tire travel after 20 rotations
Answers
Answer:
is A
Step-by-step explanation:
Give a 98% confidence interval for one population mean, given asample of 28 data points with sample mean 30.0 and sample standarddeviation s = 2.40.
Answers
We have a sample of 28 data points. The sample mean is 30.0 and the sample standard deviation is 2.40. The confidence level required is 98%. Then, we calculate α by:
\(\begin{gathered} 1-\alpha=0.98 \\ \alpha=0.02 \end{gathered}\)The confidence interval for the population mean, given the sample mean μ and the sample standard deviation σ, can be calculated as:
\(CI(\mu)=\lbrack x-Z_{1-\frac{\alpha}{2}}\cdot\frac{\sigma}{\sqrt[]{n}},x+Z_{1-\frac{\alpha}{2}}\cdot\frac{\sigma}{\sqrt[]{n}}\rbrack\)Where n is the sample size, and Z is the z-score for 1 - α/2. Using the known values:
\(CI(\mu)=\lbrack30.0-Z_{0.99}\cdot\frac{2.40}{\sqrt[]{28}},30.0+Z_{0.99}\cdot\frac{2.40}{\sqrt[]{28}}\rbrack\)Where (from tables):
\(Z_{0.99}=2.33\)Finally, the interval at 98% confidence level is:
\(CI(\mu)=\lbrack28.94,31.06\rbrack\)Find the height of a cone with a volume of 464.603 cubic feet and a diameter of 8 feet.
Answers
27.75 feet
Step-by-step explanation:
d = 2r = 8 => r = 4 feet
V = 464.603 = πr²h/3
464.603·3=3.14·16·h =>
h = 1393.809 : 50.24
h ≈ 27.75 feet
we know it has a diameter of 8, thus its radius is half that or namely 4.
\(\textit{volume of a cone}\\\\ V=\cfrac{\pi r^2 h}{3}~~ \begin{cases} h=height\\ r=radius\\[-0.5em] \hrulefill\\ r=4\\ V=464.603 \end{cases}\implies 464.603=\cfrac{\pi (4)^2 h}{3} \\\\\\ 3(464.603)=\pi (4)^2 h\implies \cfrac{3(464.603)}{\pi (4)^2}=h\implies 27.73\approx h\)
I NEED HELP ASAP PLS HURRY


Answers
Answer: C
Step-by-step explanation: The slope of Function A is 6 and the slope of Function B is 5.
The data below shows the recorded weights, in grams, of a random sample of apples. Using the data's mean weight, estimate the mean weight of the population of apples. Round to the nearest tenth.
33.2, 38.6, 41.9, 44.0, 42.9, 36.2, 41.7, 39.8, 43.5, 44.5, 30.5, 39.2
The mean weight of the entire population of apples is approximately __________________ grams.
Answers
The mean of the given data is approximately 39.7.
What is MeanThe mean is the mathematical average of a set of two or more numbers. The arithmetic mean and the geometric mean are two types of mean that can be calculated. The formula for calculating the arithmetic mean is to add up the numbers in a set and divide by the total quantity of numbers in the set.
In the given data set, the mean can be calculated as the sum of all the values divided by the number of entity in the data.
mean = {33.2+38.6+41.9+44.0+42.9+36.2+41.7+39.8+43.5+30.5+39.2} / 12
mean = 119 / 3
mean = 39.7
The mean of the data set is calculated as 39.66666 which is approximately 39.7.
Learn more on mean here;
https://brainly.com/question/1136789
#SPJ1
Convert the integral ∫∫ r √4 −x2−y2da where r = {(x, y) : x2 y2≤ 4, x ≥ 0} to polar coordinates, and then evaluate.
Answers
The integral ∫∫ r √4 −x2−y2da where r = {(x, y) : x2 y2≤ 4, x ≥ 0} conversion to polar coordinates the value of the integral is (4/3)π.
To convert the integral to polar coordinates, we need to express the limits of integration in terms of the polar coordinates.
Recall that in polar coordinates, x = r cosθ and y = r sinθ, where r is the radial distance from the origin and θ is the angle measured counterclockwise from the positive x-axis to the line connecting the origin to the point (x, y).
In this case, the region r is defined by \(x^2 + y^2\) ≤ 4 and x ≥ 0. In polar coordinates, this corresponds to the region 0 ≤ r ≤ 2 and 0 ≤ θ ≤ π/2. To see why, note that x ≥ 0 implies 0 ≤ θ ≤ π/2, and \(x^2 + y^2 = r^2\), so r ≤ √4 = 2.
So we have:
∫∫ r √4 −x2−y2da = ∫(θ=0 to π/2) ∫(r=0 to 2) r√(4-\(r^2\)) dr dθ
To evaluate this integral, we can use the substitution u = 4 - \(r^2\), du = -2r dr, which gives:
∫∫ r √4 −x2−y2da = ∫(θ=0 to π/2) ∫(u=4 to 0) -1/2 √u du dθ
Now we can evaluate the inner integral:
∫(u=4 to 0) -1/2 √u du = [-1/3 u^(3/2)](u=4 to 0) = (1/3)(8 - 0) = 8/3
Substituting this back into the original integral, we have:
∫∫ r √4 −x2−y2da = ∫(θ=0 to π/2) (8/3) dθ = (8/3) (π/2 - 0) = (4/3)π
Therefore, the value of the integral is (4/3)π.
For more details regarding integral, visit:
https://brainly.com/question/18125359
#SPJ1
John is digging a rectangular hole. The area of the rectangle is 8 square feet. John digs 4 feet down into the ground. What is the volume of John's hole in cubic feet?
Answers
Answer:
32 cubic feet
Step-by-step explanation:
To know the volume of a figure we have to calculate the area of its "base" and then multiply it by its height.
In this case we have a rectangular hole that has an area of 8 square feet.
As we said before:
Volume = Area x height.
If we substitute the value of the area of the rectangle and the height (or depth in this case) we would get:
Volume = 8 x 4 = 32 cubic feet.
Thus, the volume of John's hole is 32 cubic feet.
Answer:
32 cubic feet
Step-by-step explanation:
The volume of a rectangular prism is given by;
Length*width*Height
or, Area*height
Height = 4 feet
Area= 8 square feet
Conversion to Cubic feet is given by;
(cubic feet) = (square feet) × (height in feet)
Therefore,
Cubic feet = 8 square feet*4 feet
= 32 cubic feet.
1/3|x+2| is less than equal to 1

Answers
Answer: the answer is 2/3. Hope this helps :)
Please help. I don’t understand

Answers
to get the area you multiply the sides and you can represent that with parentheses
hope this helps
Answer:
(x+6)×4 or 4x +24 (hope this helps)
A firm experiences_______ if inputs are doubled and output more than doubles. diminishing marginal rate of technical substitution diminishing marginal product decreasing returns to scale increasing returns to scale
Answers
A firm experiences increasing returns to scale if inputs are doubled and output more than doubles.
When the firm's output grows at a faster rate than the growth in inputs, increasing returns to scale result. In this case, the company experiences economies of scale, which makes it more effective as it grows its production.
The firm is able to boost productivity and efficiency as it expands its scale of operations if inputs are doubled and output more than doubles.
This can be ascribed to a number of things, including specialisation, labour division, the use of capital-intensive technology, discounts for bulk purchases, and spreading fixed costs over a higher output. Lower average costs per unit of output result in higher profitability and competitiveness for the company.
The firm gains a number of benefits from growing returns to scale. First off, it lets the company to benefit from cost savings brought about by economies of scale, allowing it to manufacture goods or services for less money per unit. This may enable more competitive pricing on the market or result in larger profit margins.
Second, raising returns to scale can result in better operational effectiveness and resource utilisation. As the company grows in size, it will be able to use resources more wisely and profit from production volume-related synergies.market prices that are competitive.
For more such question on doubled visit:
https://brainly.com/question/30599213
#SPJ8
A cylinder has a height of 14 centimeters and a diameter of 16 centimeters. What is its
volume? Use a ~ 3.14 and round your answer to the nearest hundredth.
Answers
Answer:
Step-by-step explanation:
\(Solution,\\Height(h)=14cm\\Diameter(d)=16cm\\Radius(r)=16cm/2=8cm\\\\Now,\\\\Volume=\pi r^{2}h \\\\Volume=3.14*(8cm)^{2} *14cm\\\\Volume=2813.44cm^{3}\)
How many different triangles can you make if you are given the measurments or two sides an angle that is not between those two sides
Answers
Answer:
2.
Step-by-step explanation:
This is called the ambibuous case where 2 sides are given and angle opposite one of these sides.
2 traingles are possible.
Hey help but no links!!

Answers
-19.5 divided by 3 is -6.5
1 meter = 3.3 ft how many does 8 =?
Answers
Answer: 26.4 ft.
Step-by-step explanation: To find the numerical value of 8 meters in feet you need to use unit multipliers. In this case, you need to multiply 8 meters by 3.3 ft / 1 meter. This would cancel out the meters, making the unit feet. 8*3.3 = 26.4, so the answer is 26.4 ft.
quota sampling produces the same advantages for convenience sampling that ____ sampling produces for probability sampling.
Answers
The quota sampling produces the same advantages for convenience sampling that stratified random sampling produces for probability sampling.
Sampling:
Sampling is defined as the process in statistical analysis where researchers take a predetermined number of observations from a larger population.
Given,
Here we need to find the type of sampling that produces the same advantages for convenience sampling quota sampling.
Before, move on to the result, first we have to know the details about quota sampling and the probability sampling.
Probability sampling defined as the selection of a sample from a determined number of population, when this selection is based on the principle of randomization, that is, random selection or chance.
In contrast to probability sampling, Quota sampling means a non-probability sampling method in which researchers create a sample involving individuals that represent a population.
Based on these definition we have identified that the method that is best suitable answer for this one is stratified random sampling.
Because the stratified random sampling means, is a probability sampling technique in which the total population is divided into homogenous groups to complete the sampling process.
To know more about Sampling here.
https://brainly.com/question/13287171
#SPJ1
if a1=5 and an=an-1 -1 then find the value of a4
Answers
a4 = 2
It is given that,
\(a_{1} = 5\), and
\(a_{n} = (a_{n-1}) - 1\)
Therefore, it can be said,
\(a_{2} = a_{1} - 1\\a_{3} = a_{2} - 1\\a_{4} = a_{3} - 1\\\)
That is,
\(a_{2} = 5-1=4\\a_{3} = 4-1=3\\a_{4} = 3-1=2\)
So, a4 = 2
Read more about Arithmetic progression at:
https://brainly.com/question/16954227
Decide whether the primary or secondary data is most suited for the hypothesis below.
There are more students in Year 9 at your school who would prefer a trip to Thorpe Park rather than a museum.
Explain your answer in the comment box.
Primary or Secondary
Answers
To accurately assess whether there are more Year 9 students who prefer a trip to Thorpe Park rather than a museum, primary data collection methods would be more appropriate.
In this case, primary data would be most suited for testing the hypothesis.
Primary data refers to information that is collected firsthand, specifically for the purpose of addressing a research question or hypothesis. In this scenario, to determine whether there are more students in Year 9 who would prefer a trip to Thorpe Park rather than a museum, it would be necessary to directly gather data from the students themselves.
This can be done through methods such as surveys, questionnaires, or interviews. By directly asking the Year 9 students about their preferences between a trip to Thorpe Park and a museum, we can collect primary data that specifically relates to the hypothesis being tested.
On the other hand, secondary data refers to information that has already been collected by someone else for a different purpose. While there may be existing secondary data that provides general information about student preferences or visitor statistics for Thorpe Park and museums, it may not provide the specific data needed to test the hypothesis in this case.
Therefore, to accurately assess whether there are more Year 9 students who prefer a trip to Thorpe Park rather than a museum, primary data collection methods would be more appropriate.
for such more question on primary data
https://brainly.com/question/26711803
#SPJ8
DOES ANYONE UNDERSTAND QUADRATIC APPLICATIONS FOR ALGEBRA 1???? PLS DONT RESOND IF YOU DINT KNOW

Answers
Answer:
1 ) Vertex form.
2 ) Standard form.
3 ) I'm not sure about this one, but there are only 3 forms, in which the last one is factored form, and the other two are above, so it must be factored form.
Step-by-step explanation:
1 ) Vertex form : y = a( x - h )² + k
Vertex form shows you where the vertex(the lowest/highest point aka ( h, k ) ) of the parabola is, without graphing it. (But you could graph it and find the vertex like that, I recommend you use desmos graphing)
2 )Standard form : y = ax² + bx + c
Standard form can be used to show the y-intercept( aka c ), in this case, where the snowball was thrown from. (Again, you can graph it and find where he parabola hits the y axis)
3 ) Factored form : ( ax + c )( bx + d )
Factored form tells us the x-intercepts, or in this case where the snowball landed or how long the snowball is in the air. (like i said, you could graph it, and find the points(there could be only one or maybe none in some cases) that are on the x axis)
I know this was four days ago, but I hope this helped you understand a little better.
Pls help will mark Brainly est pls help 100 points please

Answers
1. Another point on the graph p(x) is (5, 9)
2. the vertex of the q(x) is (4, 10).
The other two points on the q(x) are (0, 2) and (2, 8).
What is a parabola?Parabola is a curve drawn in a plane. Where any point is at an equal distance from a fixed point (the focus ) and a fixed straight line (the directrix ).
Given:
The two equations of the quadratic functions are;
p(x) = -(x - 1)² + 10
q(x) = 1/2(x - 4)² + 10.,
The graph of p(x) and q(x) is given in the image below.
1. Another point on the graph p(x) is (5, 9)
2. the vertex of the q(x) is (4, 10).
The other two points on the q(x) are (0, 2) and (2, 8).
3. Yes the assumption is correct.
Therefore, all the required values are given above.
To learn more about parabolas;
https://brainly.com/question/21685473
#SPJ1


Consider the following.
x = 6 cosh(t), y = 2 sinh(t)
(a) Eliminate the parameter to find a Cartesian equation of the curve.
(b) Sketch the curve and indicate with an arrow the direction in which the curve is traced as the parameter increases.
Answers
The Cartesian equation for the curve is x² - 9y² = 36.
To eliminate the parameter and find a Cartesian equation for the curve defined by the parametric equations x = 6 cosh(t) and y = 2 sinh(t), we can use the hyperbolic identity cosh²(t) - sinh²(t) = 1.
(a) Eliminating the parameter:
Start by squaring both equations:
x² = 36 cosh²(t)
y² = 4 sinh²(t)
Now, divide x² by 36 and y² by 4:
x²/36 = cosh²(t)
y²/4 = sinh²(t)
Next, substitute cosh²(t) with (x²/36) and sinh²(t) with (y²/4) using the hyperbolic identity:
(x²/36) - (y²/4) = 1
Multiply through by 36 to get rid of the fraction:
x² - 9y² = 36
Therefore, the Cartesian equation for the curve is x² - 9y² = 36.
(b) Sketching the curve and indicating the direction:
The equation x² - 9y² = 36 represents a hyperbola centered at the origin, with the x-axis as the transverse axis and the y-axis as the conjugate axis.
The curve starts at the point (6, 0) when t = 0 and moves towards positive y-values as the parameter t increases. As t increases, the curve traces the upper branch of the hyperbola. The direction of the curve can be indicated by an arrow pointing upwards.
The curve starts at the point (6, 0) and moves upwards along the upper branch of the hyperbola as the parameter increases.
To know more about Cartesian visit :
brainly.com/question/29298525
#SPJ4

Which system of equations is equivalent to the following system? 2x 4y = 14 4x y = 20 2x 4y = 14 â’16x â’ 4y = â’80 2x 4y = 14 â’4x y = â’20 4x 8y = â’28 4x y = 20 â’2x â’ 4y = 14 4x y = 20.
Answers
The equivalent equations of \(2x+ 4y = 14\) and \(4x + y = 20\)
are \(2x+ 4y = 14\) and\(-16x -4y = -80\)
The system of equations is given as:
\(2x+ 4y = 14\)
\(4x + y = 20\)
Multiply both sides of the equations by -4.
So, we have:
\(-4 \times (4x + y) = -4 \times 20\)
Distribute the expression
\(-4 \times 4x -4 \times y = -4 \times 20\)
Evaluate all products
\(-16x -4y = -80\)
So, we have the following system of equations
\(2x+ 4y = 14\)
\(-16x -4y = -80\)
Hence, the equivalent equations are \(2x+ 4y = 14\) and\(-16x -4y = -80\)
Read more about equivalent equations at:
https://brainly.com/question/9603710
