Answers
Related Questions
How to solve using quadratic equations 4x^2+7x-20=0
Answers
Answer:
Step-by-step explanation:
Y = Ax2 Bx C
Enter coefficients here >>> 4 7 -20
Standard Form: y = 4x²+7x-20
1.75 0.875 0.765625 3.0625 -23.0625
Grouped Form: No valid Grouping
Graphing Form: y = 4(x+0.88)²-23.06
Factored Form: PRIME
Solution/X-Intercepts: -3.28 AND 1.53
Discriminate =369 is positive, two real solutions
VERTEX: (-0.88,-23.06) Directrix: Y=-23.13

Graph problem below. Draw and label your graph neatly.slope: -1/42y-intercept= 2
Answers
Explanation:
The equation of the line is:
y = mx + b
Where m is the slope and b is the y-intercept. So, replacing m = -1/42 and b = 2, we get:
y = (-1/42)x + 2
Then, to graph the function, we need to indentify two points. So, given the values of x, we can calculate y as follows
If x = 0
y = (-1/42)(0) + 2
y = 0 + 2 = 2
If x = 42
y = (-1/42)(42) + 2
y = -1 + 2 = 1
Therefore, the graph passes through the points (0, 2) and (42, 1).
Answer:
So, the graph is:

You are given the steps for using a compass and a straightedge to construct a line perpendicular to a given line through a point not lying on the given line. Arrange the steps in the proper sequence.
Place the compass needle on the external
point R. Make the compass width greater
than the distance from R to the given line.
Draw an arc cutting the given line at
two points. Mark and label the points
of intersection P and Q.
Draw a line from the external point R to
the point where the arcs intersect, S.
Line RS is perpendicular to line PQ and
passes through the external point R.
Move the compass needle to P and make an
arc below the line. Keep the compass width,
and move the compass needle to Q. Draw an
arc below the line crossing the other arc.
Mark and label the point of intersection S.


Answers
The proper steps for the construction are given as 1, 2 4, and then 3.
Write the steps for construction?The proper steps for the construction are;
1. Place the compass needle on the external point R. Make the compass width greater than the distance from R to the given line.
2. Draw an arc cutting the given line at two points. Mark and label the points of intersection P and Q.
3. Move the compass needle to P and make an arc below the line. Keep the compass width, and move the compass needle to Q. Draw an arc below the line crossing the other arc. Mark and label the point of intersection S.
4. Draw a line from the external point R to the points where the arcs intersect, S. Line RS is perpendicular to line PQ and passes through the external point R.
Learn more about construction;
https://brainly.com/question/6393210
#SPJ1
The milligrams of aspirin in a person's body is given by the equation a = 500*(3/4^t), where t is the number of hours since the patient took the medicine.
In the equation, what does 500 tell us about the situation?
SOMEONE ANSWER PLS!!
Answers
500 represents the initial amount of medication, since when t=0, a=500.
Which function is graphed?

Answers
Answer:
a
Step-by-step explanation
The plotted upon graph function is y = {x² + 2, x < 1 and -x + 2, x ≥ 2}.
The correct option is A.
What is a quadratic function?A polynomial function with one or more variables, where the largest exponent of the variable is two, is referred to as a quadratic function. In other terms, a "polynomial function of degree 2" is a quadratic function.
Given:
The graph of the function is given:
And function is a piecewise function.
The upper quadratic function defined over the domain x < 1.
And line function define over the domain x ≥ 2.
The function that satisfies the domain is,
y = {x² + 2, x < 1 and -x + 2, x ≥ 2}
Therefore, the function is y = {x² + 2, x < 1 and -x + 2, x ≥ 2}
To learn more about the quadratic function;
https://brainly.com/question/11485644
#SPJ2
Which statement about the location of √7 on the number line is true?
A= It is located at the number 7 on the number line.
B= It is located at the number 3.5 on the number line.
C= It is located between the numbers 2 and 3 on the number line.
D=It is located between the numbers 4 and 9 on the number line
Answers
Explanation
The square root of a number is “what number times itself”
2 x 2 = 4
3 x 3 = 9
7 is between 4 and 9 so C is the correct answer
Solve the equation using the quadratic formula.
x^2+ 11x + 9 = 0
The solution set is
Answers
\( \huge \boxed{\mathfrak{Question} \downarrow}\)
Solve the equation using the quadratic formula ⇨ x² + 11x + 9 = 0
\( \large \boxed{\mathfrak{Answer \: with \: Explanation} \downarrow}\)
\( \sf \: x ^ { 2 } + 11 x + 9 = 0\)
All equations of the form \(\sf\:ax^{2}+bx+c=0\) can be solved using the quadratic formula: \(\sf\frac{-b±\sqrt{b^{2}-4ac}}{2a}\). The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction.
\( \sf \: x^{2}+11x+9=0 \)
This equation is in standard form: ax² + bx + c = 0. Substitute 1 for a, 11 for b and 9 for c in the quadratic formula \(\sf\frac{-b±\sqrt{b^{2}-4ac}}{2a}\).
\( \sf \: x=\frac{-11±\sqrt{11^{2}-4\times 9}}{2} \\ \)
Square 11.
\( \sf \: x=\frac{-11±\sqrt{121-4\times 9}}{2} \\ \)
Multiply -4 times 9.
\( \sf \: x=\frac{-11±\sqrt{121-36}}{2} \\ \)
Add 121 to -36.
\( \sf \: x=\frac{-11±\sqrt{85}}{2} \\ \)
Now solve the equation \(\sf\:x=\frac{-11±\sqrt{85}}{2}\) when ± is plus. Add -11 to √85.
\( \boxed{ \boxed{\bf \: x=\frac{\sqrt{85}-11}{2} }}\)
Now solve the equation \(\sf\:x=\frac{-11±\sqrt{85}}{2}\) when ± is minus. Subtract √85 from -11.
\( \boxed{ \boxed{\bf \: x=\frac{-\sqrt{85}-11}{2}} } \\ \)
The equation is now solved. The solution set is :-
\(\bf \: x=\frac{\sqrt{85}-11}{2} \\ \\ \sf \: and \\ \\ \bf \: x=\frac{-\sqrt{85}-11}{2} \)
NEED ANSWERS ASAP PLS HELP
Answers
Mofor has homework assignments in five subjects. He only has time to do two of
them.
Answers
The decision of which two homework assignments to complete depends on Mofor's individual circumstances and priorities.
If Mofor only has time to do two homework assignments out of the five subjects, he will need to choose which subjects to prioritize. The specific subjects he chooses to work on will depend on various factors such as his strengths, weaknesses, upcoming deadlines, and personal preferences. Here are a few strategies he could consider:
1. Prioritize based on importance: Mofor can prioritize the homework assignments that carry more weight in terms of grades or have upcoming deadlines. This way, he ensures that he completes the assignments that have a higher impact on his overall academic performance.
2. Focus on challenging subjects: If Mofor finds certain subjects more difficult or time-consuming, he can prioritize those assignments to allocate more time and effort to them. This approach allows him to concentrate on improving his understanding and performance in subjects that require extra attention.
3. Balance workload: Mofor can choose to distribute his efforts evenly across subjects, selecting two assignments from different subjects. This strategy ensures that he maintains a balanced workload and avoids neglecting any particular subject.
The decision of which two homework assignments to complete depends on Mofor's individual circumstances and priorities. It is essential for him to consider his academic goals, time constraints, and personal strengths to make an informed decision.
For more such questions on homework
https://brainly.com/question/28521601
#SPJ8
The area of a rectangular room is 750 square feet. The width of the room is 5 feet less than the length of the room. Which equations can be used to solve for y, the length of the room? Select three options.
y(y + 5) = 750
y2 – 5y = 750
750 – y(y – 5) = 0
y(y – 5) + 750 = 0
(y + 25)(y – 30) = 0
Answers
The equations that can be used to solve for y, the length of the room, are: y(y + 5) = 750, y² – 5y = 750, and y(y – 5) + 750 = 0.
What is distributive property?It states that when multiplying a number by a group of numbers added together, you can multiply the number by each individual number in the group and add the products together to get the same answer.
In order to find the length of the room, we need to solve for y in each of the equations given.
First, let's solve for y in the equation y(y + 5) = 750. We can use the distributive property to expand the equation to y² + 5y = 750.
Then, we can subtract 750 from both sides of the equation to get y² + 5y - 750 = 0.
To solve the equation, we need to factor it. We can use the difference of squares formula to factor the equation, yielding (y + 25)(y - 30) = 0. Therefore, one solution for y is y = -25, and the other solution is y = 30.
Second, let's solve for y in the equation y² – 5y = 750.
To solve this equation, we can add 5y to both sides to get y² = 5y + 750. Then, we can divide both sides by y to get y = 5y + 750.
We can then subtract 5y from both sides to get y - 5y = 750. Finally, we can divide both sides by 5 to get y = 150.
Third, let's solve for y in the equation y(y – 5) + 750 = 0.
To solve this equation, we can use the distributive property to expand the equation to y² – 5y + 750 = 0.
Then, we can subtract 750 from both sides to get y² – 5y = -750.
To solve the equation, we need to factor it. We can use the difference of squares formula to factor the equation, yielding (y + 25)(y - 30) = 0. Therefore, one solution for y is y = -25, and the other solution is y = 30.
In conclusion, the equations that can be used to solve for y, the length of the room, are y(y + 5) = 750, y2 – 5y = 750, and y(y – 5) + 750 = 0. The solutions for y are y = -25 and y = 30.
For more questions related to numbers
https://brainly.com/question/251701
#SPJ1
Determine the equation (picture).

Answers
The line perpendicular to the equation and has the same y-intercept with another is y = - 4 / 3 x + 4.
How to find equation of a line?The equation of a line can be describe as follows:
y = mx + b
where
m = slopeb = y-interceptTherefore, lines that a perpendicular follows the rule below:
m₁m₂ = -1
Hence,
y + 6 = 3 / 4 (x - 2)
y + 6 = 3 / 4 x - 6 / 4
y = 3 / 4 x - 6 / 4 - 6
y = 3 / 4 x - 30 / 4
y = 3 / 4 x - 15 / 2
Hence,
3 / 4 m₂ = -1
m₂ = - 4 / 3
Therefore,
slope of the line is - 4 / 3
Let's find the y-intercept of the second line
4x + 5y -20 = 0
5y = -4x + 20
y = -4 / 5 x + 4
y-intercept = 4
Therefore, the line perpendicular to the equation and has the same y-intercept with another is y = - 4 / 3 x + 4.
learn more on equation here: https://brainly.com/question/14005330
#SPJ1
Can anyone help me I am stuck on this question! and tysm for the people who helped me! <3 Have a nice day!

Answers
Answer:
115.24
Step-by-step explanation:
15.35*4.25=65.2375
65.2375+50=115.2375
115.2375≈ 115.24
Answer:
$84.95
Step-by-step explanation:
50+15.35=65.35
15.35+4.25=19.6
65.35+19.6=84.95
Two people are playing the game rock, paper scissors. In each round both players show rock, paper, or scissors at the same time. What is the probability that both players show rock in the first round. Show your work.
Answers
The probability that both players show rock in the first round is 1/9 or 0.1111 (rounded to four decimal places).
In rock, paper, scissors there are three possible outcomes for each player: rock, paper, or scissors. Assuming both players choose randomly and independently of each other, each player has a 1/3 chance of showing rock in the first round.
To find the probability that both players show rock in the first round, we can use the multiplication rule of probability for independent events. The multiplication rule states that the probability of the intersection of two independent events is the product of their probabilities.
Therefore, the probability that both players show rock in the first round can be calculated as follows:
P(both show rock) = P(player 1 shows rock) x P(player 2 shows rock) P(both show rock) = 1/3 x 1/3 P(both show rock) = 1/9
So the probability that both players show rock in the first round is 1/9 or approximately 0.111.
For more such question on probability
https://brainly.com/question/251701
#SPJ8
Andre makes a three-digit number.
All the digits are odd.
The sum of the digits is 7.
What could Andre's number be?
Answers
Answer: 115,151,115,133,313,331
Step-by-step explanation:
The Andre's number can consist from 1+1+5 or 3+3+1. There are no any other sets of 3 odd digit to get 7.
Lets prove this statement.
Lets 1 of the digit is bigger than 5. However the digit is odd so it can be 7 only. However in this case the residual 2 digits are 0 . This is not possible so the gigits are odd however 0 is even.
Lets check the case when the biggest digit in the set is smaller than 3.
So it can be 1 only.
So the residual 2 digits can be 1 only. The sum of 1+1+1<7 .
SO we've prooven that the only sets of the digits are 1;1;5 or 3;3;1
The set 1;1;5 can give 3 numbers:
115,151,115
The set 1;3;3 can give 3 numbers as well:
133,313,331
if z is real then what is z*?
Answers
Answer:
Step-by-step explanation:
z is a non negitave real number
The area of a rectangle is 16 1/3 square inches.The width is 4 2/3. Inches.Find the length
Answers
Answer:
Let the length of the rectangle be L. Then we can use the formula for the area of a rectangle:
Area = Length x Width
Substituting the given values, we get:
16 1/3 = L x 4 2/3
To solve for L, we can first convert the mixed numbers to improper fractions:
16 1/3 = 49/3
4 2/3 = 14/3
Substituting these values, we get:
49/3 = L x 14/3
To solve for L, we can multiply both sides by the reciprocal of 14/3:
49/3 ÷ 14/3 = L
Simplifying, we get:
L = 49/3 x 3/14
L = 7/1
L = 7
Therefore, the length of the rectangle is 7 inches.
Step-by-step explanation:
Explain why the probability of rolling a sum from 2 to 12 is 100%. [C:2]
Answers
The probability of rolling a sum from 2 to 12 on 2 dices is 100%
Given the data,
The two dice should be rolled.
Now, there are 36 possibilities that might occur while rolling two normal six-sided dice. The reason for this is that when rolling two dice, the total number of outcomes is the product of the numbers of outcomes for each die, and each die has six potential outcomes (numbers 1 through 6).
The resultant 36 results are as follows:
1-1, 1-2, 1-3, 1-4, 1-5, 1-6
2-1, 2-2, 2-3, 2-4, 2-5, 2-6
3-1, 3-2, 3-3, 3-4, 3-5, 3-6
4-1, 4-2, 4-3, 4-4, 4-5, 4-6
5-1, 5-2, 5-3, 5-4, 5-5, 5-6
6-1, 6-2, 6-3, 6-4, 6-5, 6-6
When using two dice, there are a total of 36 possibilities that might occur.
As a result, the results' total ranges from 2 to 12.
Hence , the probability is 100 %
Click here for additional information about probability.
https://brainly.com/question/17089724
#SPJ1
Which piecewise function represents the graph?

Answers
the function that connects the point (0;1) with the point (-1;0) is the graph
Can someone help me solve this
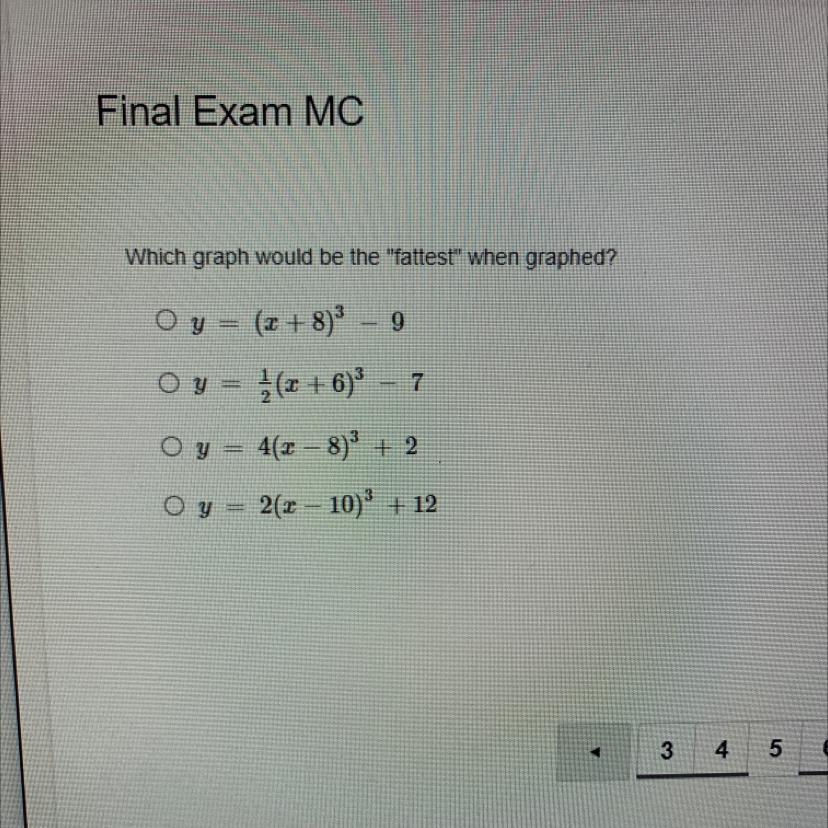
Answers
Answer:
\(y = {(x + 8)}^{3} - 9\)
Find an equation for the line below

Answers
Answer:
y = 1/2x +7/2
Step-by-step explanation:
The two marked points are 2 units apart vertically, and 4 units apart horizontally. The slope of it is ...
m = rise/run = 2/4 = 1/2
The value of the y-intercept can be found from
b = y -mx . . . . . . where (x, y) is a point on the line
Using the point (-1, 3), we find the y-intercept to be ...
b = 3 -(1/2)(-1) = 3 1/2 = 7/2
Then the slope-intercept equation is ...
y = mx +b
y = 1/2x +7/2
6) 1,1,3,8,19, 41
a) 60
b) 81
c) 90
d) 101
Analogias
Answers
The next term in the sequence is 98. None of the given options (60, 81, 90, 101) match the expected next term. None of the option is correct.
To find the pattern in the sequence 1, 1, 3, 8, 19, 41, we can examine the differences between consecutive terms:
1 1 3 8 19 41
0 2 5 11 22
Looking at the differences, we can observe that each subsequent difference is obtained by adding consecutive odd numbers: 2, 3, 4, 5, etc. This suggests that the original sequence may be related to square numbers.
Let's check if the differences between consecutive terms are square numbers:
2 = 1²
5 = 2² + 1²
11 = 3² + 2²
22 = 4² + 3²
Based on this pattern, we can make a reasonable assumption that the next difference should be 5² + 4² = 41 + 16 = 57. Adding this difference to the last term of the sequence (41), we get the next term:
41 + 57 = 98
Therefore, the next term in the sequence is 98. None of the given options (60, 81, 90, 101) match the expected next term.
Hence, none of the given options accurately continue the pattern of the sequence. It's important to note that patterns in sequences can sometimes have multiple possible interpretations, and it's always essential to consider alternative patterns or extend the sequence further to confirm the pattern.
For moresuch questions on sequence visit:
https://brainly.com/question/30762797
#SPJ8
help......................

Answers
Where the above relations are given, note that Options A, D, and E are the relations that represents a function. The others are just relations.
How do you identify the relation that represents a function?To distinguish a function from a relation, look to see if any of the x values are repeated; if not, the relationship is a function. If some x values are repeated but the accompanying y values differ, we have a relation rather than a function.
Note that where you are given domain and range, only the range is represented on the x-axis.
Some of the x values may be seen repeated in B, and C.
How is this so?
B) In a coordinate system, values are represented as (x, y). so
In relations, B 2 is repeated twice to in connection with -5, and -6. That is:
(2, -5) , (2, -6)
Since two is x, then its repetition nullified the relation as a function.
C) On table indicated on C, it is much easier to identify the x and y values. As is seen, -3 is repeated twice in connection with 4 and 2. Thus, its repetition nullified the relation as a function.
As a result, Options A, D, and E are the relations that represent a function.
Learn more about function at:
https://brainly.com/question/30721594
#SPJ1
3 6 9 12 15 18 21 24 27 30 is odd or even numbers?
Answers
Answer: Half of them are even and half of them are odd.
Step-by-step explanation:
The even numbers are 6, 12, 18, 24, and 30. An even number is defined as a number that is divisible by 2, meaning it has no remainder when divided by 2. For example, 6 divided by 2 equals 3 with no remainder, so 6 is even.
The odd numbers are 3, 9, 15, 21, and 27. An odd number is defined as a number that is not divisible by 2, meaning it has a remainder of 1 when divided by 2. For example, 9 divided by 2 equals 4 with a remainder of 1, so 9 is odd.
Therefore, out of the given numbers, half of them are even and half of them are odd.
________________________________________________________
A bose ongle in isosceles triangle measures
42° grow and label the triande
what is the measure of the vertex angle?
Answers
The measure of the vertex angle of the isosceles triangle is 96 degrees.
What is isosceles triangle?
In geometry, an isosceles triangle is a triangle that has two sides of equal length. Sometimes it is specified as having exactly two sides of equal length, and sometimes as having at least two sides of equal length, the latter version thus including the equilateral triangle as a special case.
Area: ½ × base × height
Perimeter: (2 x length of one of the long sides) + base of the isosceles triangle
We are given that;
The base angle= 42°
If an isosceles triangle has two equal angles, then the third angle (the vertex angle) must also be equal to those angles.
In this case, one of the equal angles measures 42°, so the other equal angle must also measure 42°. The sum of the angles in any triangle is 180°, so we can find the measure of the vertex angle by subtracting the sum of the two equal angles from 180°:
Vertex angle = 180° - 2(42°) = 96°
Therefore, the measure of the vertex angle in the isosceles triangle will be 96 degrees.
Learn more about isosceles right angled triangle here:
https://brainly.com/question/27190025
#SPJ9
Choose the graph of y = |x| + 3 by translating the parent function.
Answers
Answer:
picture?
Step-by-step explanation:
Answer:
Visualise the answer as a 90 degree angle, pointing downward (left side going up/left at 45 degrees, and right side going up/right at 45 degrees), with the corner falling on point 0, 3.
Find the equilibrium points of the following nonlinear system. Find its linearization at each equilibrium point. Determine the types of equilibrium points and investigate the stability.x′=y
y′=−6x−y−3x2
Find the approximate solution of the system for the initial conditions x(0)=−2.1,y(0)=0.1
.
Answers
the approximate solution for the initial conditions x(0)=-2.1, y(0)=0.1 is (-2.1, -1.91). To find the equilibrium points of the system, we set x' and y' equal to zero:
x' = y = 0
\(y' = -6x - y - 3x^2 = 0\)
From the first equation, we get y = 0. Substituting into the second equation, we have \(-6x - 3x^2 = 0\) , which gives us x = -2 or x = 0.
Therefore, the equilibrium points are (-2,0) and (0,0).
To find the linearization at each equilibrium point, we calculate the Jacobian matrix:
J = [0 1; -6-6x -1]
At (-2,0), J = [0 1; -6 -1] and at (0,0), J = [0 1; 0 -1].
To determine the type and stability of each equilibrium point, we calculate the eigenvalues of the Jacobian matrix. At (-2,0), the eigenvalues are -3 and 2, which means it is a saddle point. At (0,0), the eigenvalues are 0 and -1, which means it is a degenerate node.
To find the approximate solution of the system for the initial conditions x(0)=-2.1, y(0)=0.1, we can use numerical methods such as Euler's method or Runge-Kutta method. Here, we will use the Euler's method with step size h=0.1.
We have x(0) = -2.1 and y(0) = 0.1. Using the system of differential equations, we have:
x(0+h) = x(0) + hy(0) = -2.1 + 0.10 = -2.1
\(y(0+h) = y(0) + h*(-6x(0) - y(0) - 3x(0)^2) = 0.1 + 0.1*(-6*(-2.1) - 0.1 - 3*(-2.1)^2) = -1.91\)
Therefore, the approximate solution for the initial conditions x(0)=-2.1, y(0)=0.1 is (-2.1, -1.91).
To know more about Runge-Kutta method. click here:
brainly.com/question/31040352
#SPJ4
Find the measure of each angle indicated. Round to the nearest tenth.

Answers
The measure of the side length labelled x is 23.3 units.
What is the value of side x?The figure in the image is right triangle.
Angle A = 42°Opposite to angle A = 15,6Hypotenuse = xTo find x, we use trigonometric ratio
Sine = Opposite / Hypotenuse
Hence;
sin( 42 ) = 15.6 / x
Solve for x
x = 15.6 / sin( 42 )
x = 23.3
Therefore, the value of x is 23.3.
Learn more about trigonometric ratio here: brainly.com/question/28016662
#SPJ1
Find the domain and real zeros of the given function
F(x)= 3x-5/x^2-x-12
Answers
Answer:
DOMAIN : x ∈ (-∞ , -3 )U (4 , ∞) or {x | x ∈ R where x ≠ -3 and 4}
REAL ZEROS : x = 5/3
Step-by-step explanation:
\(f(x) = \frac{3x -5}{x^{2} -x-12}\)
factorize the bottom part
\(x^{2} - x - 12\)
product = -12 , sum = -1 , factors = -4 and 3
\(x^{2} +3x-4x-12=0\)
x (x + 3) - 4(x + 3) = 0
(x - 4) ( x + 3) = 0
x - 4 = 0 and x + 3 = 0
x = 4 and x = -3
for the function f(x) the domain is all real numbers ( R ) except - 3 and 4
Domain = x ∈ (-∞ , -3 )U (4 , ∞)
TO FIND THE ZEROS LET f(x) be equal to zero
\(0 = \frac{3x - 5}{x^{2} - x - 12}\)
cross multiply
0 = 3x - 5
find x
3x = 5
\(x = \frac{5}{3}\)
find the 12th term of the geometric sequence 1,-4,16
Answers
Answer:
common ratio =r=3
Step-by-step explanation:
Answer:
−4194304
Step-by-step explanation:
What is the image of (-1,-5) after a dilation by a scale factor of 5 centered at the
origin?

Answers
A dilation by a scale factor of 5 centered at the origin simply multplies by 5 the coordinates of every point. So, the new coordinates are (-5, -25)
