Can someone tell me the answer plz for brainlist and points to whoever gets it right

Answers
Answer:
Alonzo was right about the equations being the same because they both end up equaling up to (4,-5)
Step-by-step explanation:
I attached the work below so you also know how to do it. I hope this helps you and I hope you have an amazing night and remember to drink water and eat and get a good nights rest. and remember that school does not define how smart you are!

Related Questions
Dan was thinking of a number. Dan doubles it and gets an answer of 34.7. What was the original number?
Answers
Aidan makes 12 bracelets on Monday. He makes 8 more bracelets each day from Tuesday through Thursday. How many bracelets does Aidan have in all by the end of the day on Thursday? *
5 points
Answers
Answer:
He makes 44 bracelets on Friday.
Brainly me or heart if this helped!
Answer:
36 bracelets
Step-by-step explanation:
12+(3*8)=x
12+24=36
Aidan originally started with 12 bracelets. He makes 8 Tuesday through Thursday, which is three days. 8 * 3 is 24 plus 12 equals 36.
Does this triangle have a hypotenuse about 38 feet long

Answers
Please help me asap
tyyyyyyy :D

Answers
Answer:
7x + 2y = -6
Step-by-step explanation:
Multiply the equation with 2
2 ( y = -7x/2 - 3 )
2y = -7x - 6
7x + 2y = -6
As the density, or number of keys relative to the length of an array decreases, so does the probability of hashing collisions. O True O False
Answers
It is essential to choose a suitable hash function and carefully manage the density of keys in a hash table to ensure efficient storage and retrieval of data while minimizing the risk of collisions.
Hashing is a technique used to store and retrieve data quickly in data structures like hash tables. In a hash table, data elements are accessed based on their unique keys, which are mapped to specific locations in an underlying array using a hash function. However, if two or more keys have the same hash value, a collision occurs, and the keys must be stored in separate locations within the array.
The likelihood of collisions occurring increases as the density of keys relative to the length of the array increases. This is because the number of keys competing for the same hash bucket becomes higher, increasing the probability that two or more keys will have the same hash value. On the other hand, if the density of keys decreases, the probability of collisions also decreases. With fewer keys competing for the same buckets, each key has a better chance of being assigned a unique location within the array.
Therefore, it is essential to choose a suitable hash function and carefully manage the density of keys in a hash table to ensure efficient storage and retrieval of data while minimizing the risk of collisions.
Learn more about function here:
https://brainly.com/question/30721594
#SPJ11
Please help me need ASAPp

Answers
a tank holds 4000 liters of water in which 100 grams of salt have been dissolved. saltwater with a concentration of 1 grams/liter is pumped in at 10 liters/minute and the well mixed saltwater solution is pumped out at the same rate. write initial the value problem for:
Answers
The mass of salt in the tank at time t.
dS/dt = 10 - S/400
S(0) = 100 grams
The solution is S(t) = 4000 - 3900\(e^{\frac{-t}{400}}\)
A tank holds water V(0) = 4000 liters in which salt S(0) = 100 grams.
So dS/dt = S(in) - S(out)
S(in) = 1 × 10 = 10 gram/liters
S(out) = S/V × 10 = 10S/V gram/liters
V = V(0) + q(in) - q(out)
V = 4000 + 10t - 10t
V = 4000 liters
dS/dt = 10 - 10S/V
dS/dt = 10 - 10S/4000
dS/dt = 10 - S/400
Now given; S(0) = 100.
Here, p(t) = 1/400, q(t) = 10
\(\int p(t)dt = \int\frac{1}{400}dt\)\(\int p(t)dt = \frac{1}{400}t\)
\(\mu=e^{\int p(t)dt}\)
\(\mu=e^{\frac{t}{400}}\)
So, S(t) = \(\frac{\int\mu q(t)dt+C}{\mu}\)
S(t) = \(\frac{\int e^{\frac{t}{400}} \cdot10dt+C}{e^{\frac{t}{400}}}\)
S(t) = \(e^{\frac{-t}{400}} \left({\int e^{\frac{t}{400}} \cdot10dt+C}\right)\)
S(t) = \(e^{\frac{-t}{400}} \left({10\times\frac{e^{\frac{t}{400}}}{1/400} +C}\right)\)
S(t) = \(e^{\frac{-t}{400}} \left({4000\times{e^{\frac{t}{400}} +C}\right)\)
Now solving the bracket
S(t) = 4000 + \(e^{\frac{-t}{400}}\)C.....(1)
At S(0) = 100
100 = 4000 + \(e^{\frac{-0}{400}}\) C
100 = 4000 + \(e^{0}\) C
100 = 4000 + C
Subtract 4000 on both side, we get
C = -3900
Now S(t) = 4000 - 3900\(e^{\frac{-t}{400}}\)
To learn more about mass of salt link is here
brainly.com/question/11192688
#SPJ4
The complete question is:
A tank holds 4000 liters of water in which 100 grams of salt have been dissolved. Saltwater with a concentration of 1 grams/liter is pumped in at 10 liters/minute and the well mixed saltwater solution is pumped out at the same rate. Write initial the value problem for:
The mass of salt in the tank at time t.
dS/dt =
S(0) =
The solution is S(t) =
find the sum (3x^2+2x+3)+(x^2+x1)
Answers
The sum of (3x² + 2x + 3) + (x² + 1) will be 4x² + 2x + 4.
How to calculate the sum?The sum of (3x² + 2x + 3) + (x² + 1) will be calculated by simply adding the values.
This will be:
= (3x² + 2x + 3) + (x² + 1)
= 3x² + x² + 2x + 3 + 1
= 4x² + 2x + 4
Learn more about sum on:
brainly.com/question/24205483
#SPJ1
A chord is 80 inches long. It is 96 inches from the center of the circle. What is the radius of the circle?
Answers
Answer:
104 inches
Step-by-step explanation:
To solve this, we use a circle theorem. The circle theorem to use is that a line from the center of a circle is perpendicular to a chord and it divides the chord into exactly two equal parts.
So therefore, we shall be having a right angled triangle if we join the edge of the chord to the center of the circle.
So in this circle, we have the distance from the center of the circle to the chord, the radius of the circle and half the length of the chord.
The length of the radius serves as the hypotenuse.
Let’s call the radius r.
The other two sides measure; 40 and 96 respectively.
Mathematically, using Pythagoras’ theorem which states that the square of the hypotenuse equals the sum of the squares of the two other sides;
r^2 = 40^2 + 96^2
r^2 = 10,816
r = √(10,816)
r = 104 inches
What are the equations of lines m and q?
The equation of line m is:

Answers
Answer:
Equation of 'm'
(y - 6) = - ³/₅ (x - 2) [point-slope form]
y = - ³/₅ x + ³⁶/₅ [slope-intercept form]
Equation of 'q'
(y - 6) = ⁵/₃ (x - 2) [point-slope form]
y = ⁵/₃ x + ⁸/₃ [slope-intercept form]
Step-by-step explanation:
To find the equation for both 'm' and 'q' requires a bit of work. Because neither 'm' nor 'q' has two points to find the slopes of the line, we have to get creative.
Line 'n' has two points [ (4, 4) & (1, -1) ], and as such we can find the slope of that line. Luckily for us, line 'n' is parallel with 'q' and perpendicular with m.
Finding the slope of 'n'
The slope of the 'n' = (y₂ - y₁) ÷ (x₂ - x₁)
= (4 - (- 1)) ÷ (4 - 1)
= 5 ÷ 3
= ⁵/₃
Determine the slope of 'q' and 'm'
When two lines are parallel, they have the same slope.Since 'n' and 'q' are parallel,
then the slope of q = ⁵/₃
When two lines are perpendicular, the product of their slopes is -1. This means that the slopes are negative-reciprocals of each other.Since 'n' and 'm' are perpendicular
then the slope of m = - ³/₅
Write the equation for 'q' and 'm'
We can now use the point-slope form (y - y₁) = m(x - x₁)) to write the equation for the lines
For both 'q' and 'm' let (x₁, y₁) be (2, 6)
Equation of 'm'
(y - 6) = - ³/₅ (x - 2) [point-slope form]
y = - ³/₅ x + ³⁶/₅ [slope-intercept form]
Equation of 'q'
(y - 6) = ⁵/₃ (x - 2) [point-slope form]
y = ⁵/₃ x + ⁸/₃ [slope-intercept form]
how did you find the b in y = mx + b for both lines m and n?
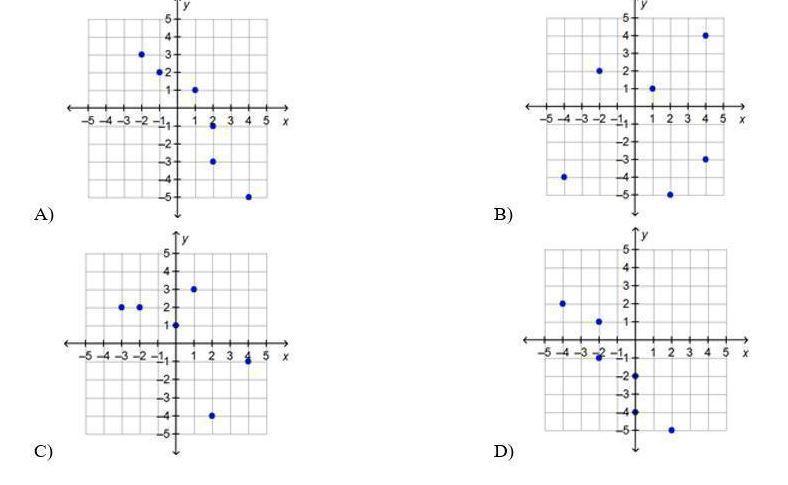
Which graph shows a set of ordered pairs that represent a function?
3
2
1 .
5-4-3-2-11. 2.3
-2-
3+
Mark this and return
3-2.
3-
2-
4
+2+
-3-
O
123
5
34
2+
1+
4-3-2-1₁- 1 2 3 4 5
.
Save and Exit
+24
-3-
4
O
4
3-
2
44
54-3-2-11-
•
1 2 3 4 5 X
Next
Submit
Answers
The second graph shows a set of ordered pairs that represent a function.
What is function?Functions are an expression, rule, or law that defines a relationship between one variable (the independent variable) and another variable (the dependent variable).
here, we have,
A relation is a function in which every x value will have different y values, this represents "every input will have unique output" part of the definition of the function,
When we observe the graphs (attached), we will notice in graph 1) there are two ordered pairs with same x value and different y values, (2, -1) and (2, -3), which is making them out of the list of being a function,
In graph 2) we have, (-2, 2), (1, 1), (5, 4), (-4, -4), (2, -5) and (4, -3), in this all the order pairs have different x-y values, therefore, this set of ordered pairs that represent a function.
Hence, the second graph shows a set of ordered pairs that represent a function.
Learn more about functions, click;
brainly.com/question/12431044
#SPJ1
The question do not have graph, so, the question is solved for the graph attached.
Jeans are on sale with a 65% off. The jeans originally cost $72. What is the sales price?
Answers
As the sales price is 65% off you find the 65% of the original cost and then substract it from the original cost:
\(\begin{gathered} 72\cdot0.65=46.8 \\ \\ 72-46.8=25.2 \end{gathered}\)Then, the sales price is $25.2Consider the function g(x)=−(x+4)^2−7.
a. Is g(x) one-to-one?
b. Determine a restricted domain on which g(x) is one-to-one and non-decreasing. (Hint: sketching a graph can be helpful.)
Answers
The function g(x) is not one-to-one. However, a restricted domain where g(x) is one-to-one and non-decreasing is x ≤ -4.
To determine if g(x) is one-to-one, we need to check if different inputs (x-values) produce different outputs (y-values). In the case of g(x) = -(x+4)^2 - 7, we can see that different x-values can result in the same y-value. For example, if we substitute x = -5 and x = -3 into g(x), we get the same output of -7. This violates the one-to-one property. To find a restricted domain where g(x) is one-to-one and non-decreasing, we can analyze the graph of the function. The graph of g(x) is a downward-opening parabola with its vertex at (-4, -7). It is symmetric with respect to the vertical line x = -4. This symmetry indicates that the function is not one-to-one across its entire domain. However, if we restrict the domain to x ≤ -4 (including -4), we can observe that the function is one-to-one within this range. As x values decrease, the corresponding y values also decrease, making g(x) non-decreasing. In other words, within this restricted domain, different x-values will always produce different y-values, satisfying the one-to-one property.
Learn more about symmetry here:
https://brainly.com/question/1593820
#SPJ11
What is the base area.

Answers
Answer:
Area of the base is 10.5 cm².
Step-by-step explanation:
Formula for the volume of the given oblique prism = Area of the triangular base × Vertical height between two triangular bases
Vertical height = 6 cm
Volume = 63 cm³
From the formula,
63 = Area of the triangular base × 6
Area of the base = \(\frac{63}{6}\)
= 10.5 cm²
Therefore, area of the base is 10.5 cm².
Use Euler's Method with a step size of h = 0.1 to find approximate values of the solution at t = 0.1,0.2, 0.3, 0.4, and 0.5. +2y=2-ey (0) = 1 Euler method for formula Yn=Yn-1+ hF (Xn-1-Yn-1)
Answers
Using Euler's Method with a step size of h = 0.1, the approximate values of the solution at t = 0.1, 0.2, 0.3, 0.4, and 0.5 are:
t = 0.1: y ≈ 1.1
t = 0.2: y ≈ 1.22
t = 0.3: y ≈ 1.34
t = 0.4: y ≈ 1.47
t = 0.5: y ≈ 1.61
To use Euler's Method, we start with an initial condition. In this case, the given initial condition is y(0) = 1. We can then iteratively calculate the approximate values of the solution at each desired time point using the formula:
Yn = Yn-1 + h * F(Xn-1, Yn-1)
Here, h represents the step size (0.1 in this case), Xn-1 is the previous time point (t = Xn-1), Yn-1 is the solution value at the previous time point, and F(Xn-1, Yn-1) represents the derivative of the solution function.
For the given differential equation +2y = 2 - ey, we can rearrange it to the form y' = (2 - ey) / 2. The derivative function F(Xn-1, Yn-1) is then (2 - eYn-1) / 2.
Using the initial condition y(0) = 1, we can proceed with the calculations:
t = 0.1:
Y1 = Y0 + h * F(X0, Y0)
= 1 + 0.1 * [(2 - e^1) / 2]
≈ 1 + 0.1 * (2 - 0.368) / 2
≈ 1 + 0.1 * 1.316 / 2
≈ 1 + 0.1316
≈ 1.1
Similarly, we can calculate the approximate values of the solution at t = 0.2, 0.3, 0.4, and 0.5 using the same formula and previous results.
Using Euler's Method with a step size of h = 0.1, we found the approximate values of the solution at t = 0.1, 0.2, 0.3, 0.4, and 0.5 to be 1.1, 1.22, 1.34, 1.47, and 1.61, respectively.
To know more about Euler's Method visit:
https://brainly.com/question/32691755
#SPJ11
The average daily inchworm moves foot in 10 seconds. At this current rate, how long
will it take an earthworm to move 24 inches? Show your calculations. (Give your answer
in seconds)
ve won to anolleo I no slim as
os asb 'TOL
anonicolso to wore on Del 6
Answers
Answer:
20 seconds
Step-by-step explanation:
1ft in 10 seconds = 12 in / 10 sec
to get 24 inches, or 2 feet, we simply multiply that by 2:
(12 in /10 sec) * 2
24 in /20 sec
Answer:
20 seconds!
Step-by-step explanation:
A foot is equal to 12 inches meaning you take 12 and divide it by 24 to get 2 meaning its 2 feet. and if it took 10 seconds for one foot, then it will take 20 seconds for 2 feet
Explain how you would find 36x 5/6
mentally.
Answers
Answer:
In step-by-step explanation.
Step-by-step explanation:
Multiplying a fraction (like 1/2) is really just dividing by the denominator.
In this case, we can (mentally) divide 36 by 6.
36/6 = 6
So each 1/6 of 36 is 6.
Then we just add 1/6 of 36 five times to get 5/6
6+ 6+ 6+ 6+ 6 (or 6 x 5) and we get 30.
9×3=27
What dose rotations mean in math
Answers
Answer:
A rotation is a transformation that turns a figure about a fixed point called the center of rotation. • An object and its rotation are the same shape and size, but the figures may be turned in different directions. • Rotations may be clockwise or counterclockwise.
Step-by-step explanation:
Answer:it means the movitem of a figure to somewhere else
Step-by-step explanation:
an experimenter flips a coin 100 times and gets 52 heads. find the 89onfidence interval for the probability of flipping a head with this coin.
Answers
To find the 89% confidence interval for the probability of flipping a head with this coin, follow these steps:
1. Calculate the sample proportion (p-hat) by dividing the number of heads (52) by the total number of flips (100):
p-hat = 52/100 = 0.52
2. Determine the standard error (SE) by using the formula:
SE = sqrt(p-hat * (1 - p-hat) / n)
where n is the total number of flips. In this case, n = 100.
SE = sqrt(0.52 * 0.48 / 100) ≈ 0.0499
3. Find the critical value (z) corresponding to the 89% confidence interval. You can use a z-table or an online calculator to find this value. For an 89% confidence interval, the critical value is approximately 1.645.
4. Calculate the margin of error (ME) using the critical value (z) and standard error (SE):
ME = z * SE
ME = 1.645 * 0.0499 ≈ 0.0821
5. Determine the confidence interval by adding and subtracting the margin of error from the sample proportion:
Lower limit = p-hat - ME = 0.52 - 0.0821 ≈ 0.4379
Upper limit = p-hat + ME = 0.52 + 0.0821 ≈ 0.6021
So, the 89% confidence interval for the probability of flipping a head with this coin is approximately 0.4379 to 0.6021.
After Luca took his dogs on a walk,he gave them 6 dog treats.When Luca dad got home from work he gave the dogs t more treats.All together the dogs got 10 treats
Answers
Answer:
t=4
Step-by-step explanation:
6+t=10
-6 -6
t=4
Answer:
T=4
Step-by-step explanation:
t+6=10
-6
10-6=4
t=4
How do I solve this question?

Answers
Answer:
x = 7
Step-by-step explanation:
We can identify the figure formed by 2 radii, (6x - 3), and (3x + 18) as a kite because it is a quadrilateral symmetric around a center line.
The radii sides are congruent, and therefore, the other two sides must be congruent as well. So, we can solve for x by equation (6x - 3) and (3x + 18).
\(6x - 3= 3x + 18\)
↓ subtracting 3x from both sides
\(3x - 3= 18\)
↓ adding 3 to both sides
\(3x = 18 + 3\)
\(3x = 21\)
↓ dividing both sides by 3
\(\boxed{x = 7}\)

4a-b=10 . 2a + 3b=12
Answers
Answer:
a = 3
b = 2
Step-by-step explanation:
Solve 4a - b = 10 for b:
\(4a - b = 10\) \(4a - b - 4a = 10 - 4a\) (Subtract 4a from both sides)\(-b = -4a +10\) \(\frac{-b}{-1} = \frac{-4a+10}{-1}\) (Divide both sides by -1)\(b = 4a - 10\)Substitute 4a - 10 for b in 2a + 3b = 12
\(2a + 3b = 12\) \(2a + 3(4a-10)=12\) \(2a + 12a -30 = 12\) (Simplifying)\(14a - 30 = 12\) (Simplifying\(14a - 30 + 30 = 12 + 30\) (Add 30 to both sides)\(14a = 42\) \(\frac{14a}{14} = \frac{42}{14}\) (Divide both sides by 14)\(a = 3\)Substitute 3 for a in b = 4a - 10
\(b = 4a - 10\) \(b = 4(3) - 10\) \(b = 12 - 10\) \(b = 2\)Therefore, a = 3 and b = 2.
Sam built a circular fenced-in section for some of his animals. The section has a circumference of 55 meters. What is t 22 approximate area, in square meters, of the section? Use for 7. 7 A 240. 625 m2 B 962. 5 m2 C 2,376. 79 m2 D 240. 8 m2 o
Answers
The area of a circular fenced-in section for some of his animals is 240.625 square meter. So the option 1 is correct.
In the given question, we have to find the approximate area, in square meters, of the section.
Sam built a circular fenced-in section for some of his animals.
The section has a circumference of 55 meters.
As we know that, the circumference of circle = 2πr. So,
2πr = 55
Now putting, π = 22/7
2 × \(\frac{22}{7}\) × r = 55
Multiply by 7 on both side, we get
44 × r = 385
Divide by 44 on both side, we get
r = 8.75
The area of circle = π\(r^2\)
Now putting the value of r.
The area of circle = \(\frac{22}{7}\times(8.75)^2\)
The area of circle = \(\frac{22}{7}\) × 76.563
The area of circle = 240.625 square meter
Hence, the area of a circular fenced-in section for some of his animals is 240.625 square meter. So the option 1 is correct.
To learn more about area of circle link is here
brainly.com/question/28642423
#SPJ4
The complete question is:
Sam built a circular fenced-in section for some of his animals. The section has a circumference of 55 meters. What is the approximate area, in square meters, of the section? Use 22/7 for pi
1. 240.625 square m
2. 962.5 square m
3. 2,376.79 square m
4. 240.8 square m
Concept 9.5: Find x Assume that segments that appear to be tangent are tangent.

Answers
Answer:
x = 2
Step-by-step explanation:
Here's your solution
=> we know that tangents from a point to a common circle are equal
=> so, ST = SU
=> 7x - 3 = 5x + 1
=> 7x - 5x = 1 + 3
=> 2x = 4
=> x = 4/2
=> x = 2
hope it helps
Answer:
X will be 2
Step-by-step explanation:
ST=SU
7x-3=5x+1
2x=3+1
2x=4
x=4/2
x=2
hope it helps....
have a great day!!!
if x is a continuous random variable with the uniform distribution u(5.5,20.5), what is p(x<8)?
Answers
The correct value of p(x<8) is 1.875.
Define probabilityTo determine how probable something is gonna occur, use probability. It is a number between 0 and 1, where 0 denotes the absence of a possibility and 1 denotes the existence of one. By dividing the number of favorable outcomes by the entire number of potential possibilities, the probability of an occurrence is determined.
To find the probability that is greater than 8, we need to integrate this probability density function from 5.5 to 20.5:
P(X < 8) = ∫[5.5,20.5] f(x) dx
= ∫[5.5,20.5] (1/8) dx
= [x/8] from 5.5 to 20.5
= (20.5/8) - (5.5/8)
= 15/8
= 1.875.
Therefore, the correct probability is 1.875.
Learn more about probability here:
https://brainly.com/question/31391749
#SPJ4
The total charge for a yearly internet DVD rental membership is $231. A registration fee of $15 is paid up front , and the rest is paid monthly. Write an equation to determine how much new members pay each month, m.
How much do new members pay each month,m.
Answers
Answer:
89 cents.
Step-by-step explanation:
hope this helps
you have been given the following data: x 1 3 4 6 9 8 10 y 1 8 15 33 75 70 95 test to determine whether there is evidence of a linear relationship. please write the test hypothesis:
Answers
To test whether there is evidence of a linear relationship between the given data (x and y values), we can perform a hypothesis test.
Step 1: State the null hypothesis (H0) and the alternative hypothesis (H1).
H0: There is no linear relationship between x and y (i.e., the correlation coefficient, r, is equal to 0)
H1: There is a linear relationship between x and y (i.e., the correlation coefficient, r, is not equal to 0)
Step 2: Calculate the correlation coefficient, r, using the given data. You can do this using a statistical calculator or software.
Step 3: Determine the critical value for the correlation coefficient at a chosen significance level (e.g., 0.05).
Step 4: Compare the calculated correlation coefficient, r, to the critical value. If |r| is greater than the critical value, reject the null hypothesis (H0) in favor of the alternative hypothesis (H1), indicating evidence of a linear relationship. If |r| is less than or equal to the critical value, fail to reject the null hypothesis (H0), suggesting there is not enough evidence to support a linear relationship.
By following these steps, you can test the hypothesis and determine if there is evidence of a linear relationship between the given data points.
Learn more about test hypothesis here, https://brainly.com/question/15980493
#SPJ11
3 less than the square root of a number p
Answers
Answer:
what's the number? .. . mmxmxmx
how to find the hypotenuse of a triangle using trigonometry
Answers
To find the hypotenuse of a right triangle using trigonometry, we can utilize the Pythagorean theorem and the trigonometric ratios of sine, cosine, or tangent. Here's a step-by-step explanation:
1. Identify the right triangle: Ensure that the triangle has a right angle, which is a 90-degree angle.
2. Label the sides: Identify the two sides of the right triangle that are not the hypotenuse. These sides are typically referred to as the adjacent side and the opposite side.
3. Choose the appropriate trigonometric ratio: Depending on the information you have, select the appropriate trigonometric ratio that relates the sides you know.
- If you have the adjacent side and the hypotenuse, use cosine: cosθ = adjacent/hypotenuse.
- If you have the opposite side and the hypotenuse, use sine: sinθ = opposite/hypotenuse.
- If you have the opposite side and the adjacent side, use tangent: tanθ = opposite/adjacent.
4. Substitute the known values: Plug in the values you have into the trigonometric equation and solve for the unknown side (hypotenuse).
5. Apply the Pythagorean theorem: If you don't have the hypotenuse directly but know the lengths of both the adjacent and opposite sides, you can use the Pythagorean theorem, which states that the sum of the squares of the two legs (adjacent and opposite sides) is equal to the square of the hypotenuse. The formula is a² + b² = c², where c represents the hypotenuse.
6. Simplify and calculate: After substituting the known values into the equation, simplify and solve for the hypotenuse.
By following these steps and applying the appropriate trigonometric ratio or the Pythagorean theorem, you can find the length of the hypotenuse in a right triangle using trigonometry.
For more such questions on Pythagorean theorem
https://brainly.com/question/28981380
#SPJ8
You are given an integer n, followed by n lines of input (1 <= n <= 100). Each line of input contains one or several words separated with single spaces. Each word is a sequence of letters of english alphabet containing between 1 and 10 characters, inclusive. The total number of words in the input is between 1 and 100, inclusive. Your task is to reverse the order of words in each line of input, while preserving the words themselves. The lines of your output should not have any trailing or leading spaces.
Answers
Python program to illustrate a string reversing .
let , n is the variable , defined to get the input from the user in the form of integer. then creation of empty list is defined , after the method of reversing string then declared to the input string . then after reversing one more for loop is applied to get reverse value .
program to get a reverse value after using the method of reverse :
n=int(input("Enter number of Strings : ")) #defining n variable to input value array=[]#defining an empty list
print("Enter strings:") #print message
for i in range(n): #defining a loop that input string value array.append(input()) #appending value to an array
reverse=[] #defining an empty list
for i in range(len(array)): #defining loop for reverse word
s=array[i] # list value is stored in i
s variable new="" #defining a string variable
new1="" #defining a string variable
for j in range(len(s)): #defining loop to get reverse string value if(s[j]==" "): # if block is used to check such that the character is space or not
new=s[j]+new1+new #adding the character to the new string new1="" #assign,empty string to new k=j
else:
new1=new1+(s[j]) # new character is added
new=s[k+1:]+new # substring is added to new
reverse.append(new) #adding the reversed string to list
print("After reversing:")
for i in reverse: #printing all reversed strings
print(i)
hence , output is obtained after the execution of program ,
Enter number of string : 2
hello brainly
nice question
after reversal:
brainly hello
question nice
To know more about string reversing , click here:
brainly.com/question/30024070
#SPJ4