Answers
Answer:
The perimeter is 206.
Step-by-step explanation:
When given the area, height and side of the parallelogram, you would use the formula to find the perimeter: P=2a+2*A /h. a = side of the parallelogram, A = area, and h = height. When you plug in everything, you will get 206.
Related Questions
1) Given a triangle ABC, such that: BC = 6 cm; ABC = 40° and ACB = 60°. 1) Draw the triangle ABC. 2) Calculate the measure of the angle BAC. 3) The bisector of the angle BAC intersects [BC] in a point D. Show that ABD is an isosceles triangle. 4) Let M be the midpoint of the segment [AB]. Show that (MD) is the perpendicular bisector of the segment [AB]. 5) Let N be the orthogonal projection of D on (AC). Show that DM = DN.
Answers
Step-by-step explanation:
1) To draw triangle ABC, we start by drawing a line segment BC of length 6 cm. Then we draw an angle of 40° at point B, and an angle of 60° at point C. We label the intersection of the two lines as point A. This gives us triangle ABC.
```
C
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/_60° 40°\_
B A
```
2) To find the measure of angle BAC, we can use the fact that the angles in a triangle add up to 180°. Therefore, angle BAC = 180° - 40° - 60° = 80°.
3) To show that ABD is an isosceles triangle, we need to show that AB = AD. Let E be the point where the bisector of angle BAC intersects AB. Then, by the angle bisector theorem, we have:
AB/BE = AC/CE
Substituting the given values, we get:
AB/BE = AC/CE
AB/BE = 6/sin(40°)
AB = 6*sin(80°)/sin(40°)
Similarly, we can use the angle bisector theorem on triangle ACD to get:
AD/BD = AC/BC
AD/BD = 6/sin(60°)
AD = 6*sin(80°)/sin(60°)
Since AB and AD are both equal to 6*sin(80°)/sin(40°), we have shown that ABD is an isosceles triangle.
4) To show that MD is the perpendicular bisector of AB, we need to show that MD is perpendicular to AB and that MD bisects AB.
First, we can show that MD is perpendicular to AB by showing that triangle AMD is a right triangle with DM as its hypotenuse. Since M is the midpoint of AB, we have AM = MB. Also, since ABD is an isosceles triangle, we have AB = AD. Therefore, triangle AMD is isosceles, with AM = AD. Using the fact that the angles in a triangle add up to 180°, we get:
angle AMD = 180° - angle MAD - angle ADM
angle AMD = 180° - angle BAD/2 - angle ABD/2
angle AMD = 180° - 40°/2 - 80°/2
angle AMD = 90°
Therefore, we have shown that MD is perpendicular to AB.
Next, we can show that MD bisects AB by showing that AM = MB = MD. We have already shown that AM = MB. To show that AM = MD, we can use the fact that triangle AMD is isosceles to get:
AM = AD = 6*sin(80°)/sin(60°)
Therefore, we have shown that MD is the perpendicular bisector of AB.
5) Finally, to show that DM = DN, we can use the fact that triangle DNM is a right triangle with DM as its hypotenuse. Since DN is the orthogonal projection of D on AC, we have:
DN = DC*sin(60°) = 3
Using the fact that AD = 6*sin(80°)/sin(60°), we can find the length of AN:
AN = AD*sin(20°) = 6*sin(80°)/(2*sin(60°)*cos(20°)) = 3*sin(80°)/cos(20°)
Using the Pythagorean theorem on triangle AND, we get:
DM^2 = DN^2 + AN^2
DM^2 = 3^2 + (3*sin(80°)/cos(20°))^2
Simplifying, we get:
DM^2 = 9 + 9*(tan(80°))^2
DM^2 = 9 + 9*(cot(10°))^2
DM^2 = 9 + 9*(tan(80°))^2
DM^2 = 9 + 9*(cot(10°))^2
DM^2 = 9 + 9*(1/tan(10°))^2
DM^2= 9 + 9*(1/0.1763)^2
DM^2 = 9 + 228.32
DM^2 = 237.32
DM ≈ 15.4
Similarly, using the Pythagorean theorem on triangle ANC, we get:
DN^2 = AN^2 - AC^2
DN^2 = (3*sin(80°)/cos(20°))^2 - 6^2
DN^2 = 9*(sin(80°)/cos(20°))^2 - 36
DN^2 = 9*(cos(10°)/cos(20°))^2 - 36
Simplifying, we get:
DN^2 = 9*(1/sin(20°))^2 - 36
DN^2 = 9*(csc(20°))^2 - 36
DN^2 = 9*(1.0642)^2 - 36
DN^2 = 3.601
Therefore, we have:
DM^2 - DN^2 = 237.32 - 3.601 = 233.719
Since DM^2 - DN^2 = DM^2 - DM^2 = 0, we have shown that DM = DN.
Jaquan and Chelsea make cubes during math class. The surface area of Jaquan's cube is 150 square units, and the surface area of Chelsea's cube is 96 square units.
How much larger is the volume of Jaquans cube than Chelsea’s cube
Answers
Answer:
Step-by-step explanation:
A cube has six faces, so, if the area is 96cm2, then, the Area of one of the faces will be 96cm2 ÷ 6 = 16cm2
since Area = L x W = L2, then L = √16cm2 = 4cm.
Find the distance between the two points rounding to the nearest tenth (if necessary).
(−5,−9) and (−8,0)
Answers
m=(x1+x2)/2 , (y1+y2)/2 where m means midpoint. In your case it looks like this.

a statistical quality control process for cereal production measures the weight of a cereal box. the population standard deviation is known to be .06 ounces. in order to achieve a 97% confidence with a margin of error of .02 ounces, how large a sample should be used?
Answers
The sample size that should be used is 43.
Given that;
The weight of a cereal box is measured as part of a statistical quality control process for the manufacture of cereal. It is understood that the population standard deviation is 0.06 ounces. To attain a margin of error of and a confidence level of 97% 0.02 ounces.
By considering the confidence level scenario, we get to solve how large a sample should be utilized.
The significance level is (α) = 0.03 ( 97% confidence level )
The critical value is (z*) = 2.17 ( From z-table )
The population standard deviation (σ) = 0.06
The margin of error (E) = 0.02
Therefore, the required sample size is;
n = [(z* × σ)/E ]²
n = 42.383
n ≅ 43
Finally, the sample size that should be used is 43.
To learn more about confidence level click here:
brainly.com/question/9386257
#SPJ4
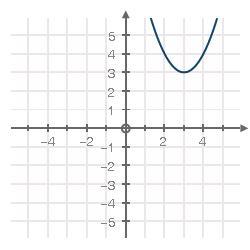
The graph of f(x) = x^2 has been shifted into the form f(x) = (x − h)2 + k:
What is the value of h?
1
-1
-3
3
Answers
Which equation was used to generate this relation?
please hurry!!!!

Answers
Answer:
y = 2x + 9
Step-by-step explanation:
1 = 2 x -4 + 9
5 = 2 x -2 + 9
9 = 2 x 0 + 9
......
The school day is 7 hours long. If recess lasts 1/4 hour, what fraction of the school day does recess make up
Answers
Answer:
recess makes up 1/28 of the school day.
Step-by-step explanation:
2020-2021 T-Math-Gr7Reg-T1 and T2-CBT: Section 1 - Students may NOT use a calculator.
Question: 1-5
Marissa found
that apply.
shirt that had a 20% markdown on it. If the price of the shirt is represented by x, how much does the shirt cost (excluding tax)? Select all
x(1.00 -0.20)
X-0.80x
X-0.20
ОООООО
0.80x
x(0.20 + 1.00)
0.20x
©
Previous
Next

Answers
Complete Question
Marissa found a shirt that had a 20% markdown on it if the price of the shirt is represented by x how much does the shirt cost excluding tax select all that apply
select all that apply
A. 0.20x
B.0.80x
C.x-0.20
D.x-0.80x
E.x(0.2+1.00)
F. x(1.00-0.20)
Answer:
B. 0.80x
F. x(1.00-0.20)
Step-by-step explanation:
The Formula for Selling Price when you have percent markdown is;
Selling price = (1 - percentage mark down)× Original price
From the question:
Selling price= Cost of the shirt(excluding tax)
Original price = x
Percentage markdown = 20%
= 0.20
Hence,
Cost of the shirt(excluding tax)
= (1 - 20%)x
= (1 - 0.20)x
= 0.80x
Option B and F is the correct option
Order from least to greatest

Answers
Answer:
(6,7,8,8,9,11)
Step-by-step explanation:
Hopefully this helps:)
Answer:
2006-6, 2005-7, 2004-8, 2002-8, 2003-9, 2001-11
solve the equation
pic:

Answers
The solution to the equation \((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2\) is 10.3891
How to solve the equationFrom the question, we have the following parameters that can be used in our computation:
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2\)
Using the following trigonometry ratio
sin²(x) + cos²(x) = 1
We have
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2 = (\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + 1 + e^2\)
The sum to infinity of a geometric series is
S = a/(1 - r)
So, we have
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2 = \frac{1/2}{1 - 1/2} + \frac{9/10}{1 - 1/10} + 1 + e^2\)
So, we have
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2 = 1 + 1 + 1 + e^2\)
Evaluate the sum
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2 = 3 + e^2\)
This gives
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2 = 10.3891\)
Hence, the solution to the equation is 10.3891
Read more about summation notation at
brainly.com/question/15973233
#SPJ1
what value of X makes this equation true? -9x+15=3(2-x)
Answers
Answer:
3/2
Hope this helps <3
Answer:
Step-by-step explanation:
Equation
-9x+15=3(2-x) Remove the brackets.
Solution
-9x + 15 = 6 - 3x Add 9x to both sides
-9x+9x + 15 = 6 - 3x + 9x Combine
15 = 6 + 6x Subtract 6 from both sides
15 - 5 = 6 -6 + 6x Combine
10 = 6x Divide by 6
10/6 = 6x/6
Answer
x = 1 2/3 or 1.66666 ...
The measures of the angles of a triangle are shown in the figure below. Solve for x
need help asap!!!)

Answers
Answer:
x=36
Step-by-step explanation:
(3x+3)^0+x+54= 90
x+54=90
x=90-54
x=36
*4) The image of the origin under a certain translation is (5,-6). The
image of point (-4,2) under the same translation is which?
(1) (1,-4)
(3) (-5,6)
4).
(2) (9,8)
(4) (-9,8)
Answers
The origin is located at (0,0). Point (5, -6) is a positive x coordinate and negative y coordinate (x,y). This means, on a graph, from 0 to 5, you move 5 units to the right on the x-axis (horizontally). Then, 0 to -6 means you move 6 units down on the y-axis (vertically).
5 right and 6 down.
This translation on point (-4, 2) can be represented by (-4 + 5, 2 -6), which is the point (1, -4).
what 3 1/2 times 2 3/4
Answers
Answer: 9/4 or 2.25
Step-by-step explanation:?????
Hope this helps :)
Brainliest plzz
20% of the tickets sold at a water park were child tickets. If the park sold 50 tickets in all,
how many child tickets did it sell?
tickets
Answers
Answer:
= 10 tickets
Step-by-step explanation:
= 20% × 50
= 20/100 × 50
= 1000/100
= 10
What percentage of Americans are self-employed?
Answers
According to the most recent data from the U.S. Bureau of Labor Statistics (BLS), as of 2020, approximately 10.1% of Americans are self-employed.
This means that out of the total U.S. population, about 1 in 10 individuals are working for themselves rather than being employed by someone else.
It is important to note that the percentage of self-employed individuals can vary depending on various factors such as economic conditions, industry trends, and personal preferences. For example, certain industries like agriculture, construction, and professional services tend to have higher rates of self-employment compared to others.
Self-employment offers individuals the opportunity to have more control over their work, set their own schedules, and potentially earn higher incomes. However, it also comes with certain challenges such as the need to handle business-related tasks like marketing, finances, and customer acquisition.
Overall, the percentage of self-employed Americans provides insights into the dynamic nature of the job market and the various ways people choose to earn a living.
Read more about the BLS at https://brainly.com/question/32104394
#SPJ11
did i do this right if not can you show me how to do it

Answers
Answer:
no
Step-by-step explanation:
Order of operations
18/2=9
9/3=3
5-2=3
3/3
1 (simplified)
The outcome is still the same but since you have to show your work.....That's the correct way to do it
Hope this helps. Have a nice day.
A data set of test scores is being transformed by applying the following rule to each of the raw scores: transformed score = 3.5(raw score) + 6.2 Which of the following is NOT true?
a. The mean transformed score equals 3.5(the mean raw score) + 6.2
b. The median transformed score equals 3.5(the median raw score) + 6.2
c. The range of the transformed scores equals 3.5(the range of the raw scores) + 6.2
d. The standard deviation of the transformed score equals 3.5(the standard deviation of the raw score)
e. The IQR of the transformed scores equals 3.5(the IQR of the raw scores)
Answers
Option C that is the range of the transformed test scores equals 3.5(the range of the raw scores) + 6.2 is NOT true
The range for a given data set is the difference between the highest and lowest data values. On transforming the scores using the new rule of transformation the highest and lowest values of the test scores also get changed. But the range of raw scores when multiplied by 3.5 and added to 6.2 will not be equal to the range of the transformed scores.
More problems in finding ranges of data sets:
brainly.com/question/15953457
#SPJ4
A city park commission received a donation of playground equipment from a parents' organization. The area of the playground needs to be 256 square yards for the children to use it safely. The playground will be rectangular. The city will pay to have soft pavement made of recycled tires installed in the playground. In the first plan, one side 8 yards longer than the other side. Which equations model the possible dimensions of the playground? x( x + 8) = 256 ( x2) - 8 = 256 x2- 8 x - 256 = 0 ( x + 4)( x - 4) = 256 x( x - 8) = 256
Answers
Answer:
x(x+8) = 256
Step-by-step explanation:
hello
one side is x
the other one is 8 yards longer, so it is x + 8
so the surface is x(x+8) = 256
hope this helps
Answer:
x(x + 8) = 256
Step-by-step explanation:
The area of a rectangle can be calculated by doing length times width.
One side is 8 yards longer than the other. Let one side be represented by x. So, another side would be x + 8.
x * (x + 8) = 256
x(x + 8) = 256
x^2 + 8x = 256
Hope this helps!
Roy has a 120-meter strip to work with.
How many 1 decimeter pieces can be cut from his strip
Answers
Answer:
1,200 one decimeter pieces can be cut
Step-by-step explanation:
Find how many 1 decimeter pieces can be cut by converting the 120 meters to decimeters.
In 1 meter, there are 10 decimeters.
So, convert 120 meters to decimeters by multiplying it by 10:
120(10)
= 1,200
So, there are 1,200 decimeters in the strip. This means that 1,200 one decimeter pieces can be cut, since 1,200 divided by 1 is 1,200.
So, 1,200 one decimeter pieces can be cut
What is 3/8 ÷ 8 simplified?
Answers
Answer:
3/64
Step-by-step explanation:
Answer: 3/64
Step-by-step explanation:
what is the meaning of interval [a,b]
Answers
Answer:
Step-by-step explanation:
interval in mathematics stands for a set of real numbers,
denoted by [a,b] where a and b are the starting and ending real numbers both inclusive respectively.
thus, interval [a,b] is the set of real numbers starting from a to b both are real numbers and are included.
At any time t > 0,the rate at which a person can memorize a list of M words is proportional to the product of the number of words memorized ad tlie number of words tlat have not been memorized. If 2 denotes the number of words memorized at time t, which differential equation models this situation? Assume kis a positive constant; A. d k dt B. d k ( - M) dt C d k(M - 2) dt D. d =Rt(M -t) dt
Answers
The differential equation that models this situation is dx/dt = kx(M - x) (option c).
To determine the differential equation that models the situation, let's analyze the problem statement.
The rate at which a person can memorize a list of M words is proportional to the product of the number of words memorized and the number of words that have not been memorized.
Let's denote the number of words memorized as "a" and the number of words not yet memorized as "M - a" (where M is the total number of words in the list).
The problem states that the rate of memorization is proportional to the product of "a" and "M - a". We can express this mathematically as:
Rate of memorization ∝ a * (M - a)
To convert this proportionality into an equation, we introduce a positive constant k:
Rate of memorization = k * a * (M - a)
The left side of the equation represents the rate of change of the number of words memorized (da/dt), and the right side represents the product of "a" and "M - a" multiplied by the constant k.
Therefore, the differential equation that models this situation is:
da/dt = k * a * (M - a)
Comparing this with the given options, we can see that the correct choice is option C:
dx/dt = k * x * (M - x)
The complete question is:
At any time t > 0 the rate at which a person can memorize a list of M words is proportional to the product of the number of words memorized and the number of words that have not been memorized. If a denotes the number of words memorized at time t, which differential equation models this situation? Assume k is a positive constant.
A. dx/dt = kx
B. dx/dt = kx(x - M)
C. dx/dt = kx(M - x)
D. dx/dt = kt(M - t)
To know more about differential equation:
https://brainly.com/question/32524608
#SPJ4
The absolute value of (2−7)=
Answers
That because anything in the absolute value that is a negative answer it will always be positive. Like 2-7 which supposed to equal to -5 but when it come in a absolute value the answer will be positive 5.
The absolute value is:
5Work/explanation:
First, we will evaluate 2-7.
It evaluates to -5.
Now, let's find the absolute value of -5 by using these rules:
\(\sf{\mid a\mid=a}\)
\(\sf{\mid-a \mid=a}\)
Similarly, the absolute value of -5 is:
\(\sf{\mid-5\mid=5}\)
Hence, 5 is the answer.Can someone help me ? I don’t get this

Answers
The given equation according to the BODMAS become 39 in the simplified form.
According to the statement
we have to solve the given equation and simplify this.
So, For this purpose,
The given information is:
The equation is 40-32÷8+5-2.
Here to solve the equation we use the BODMAS rule:
So, The BODMAS rule states that mathematical expressions with multiple operators need to be solved from left to right in the order of BODMAS.
So, the equation is
40-32÷8+5-2.
Firstly we divide 32 and 8 according to the rule.
So,The equation become
40-4+5-2.
Then we add the terms then the equation become:
40+1-2.
Then again we add the terms then the equation become:
41-2.
Then we subtract the term then
39.
So, The given equation according to the BODMAS become 39 in the simplified form.
Learn more about BODMAS here
https://brainly.com/question/16788360
#SPJ1
The band is selling tickets to their spring show. The auditorium holds 1200 people. What is the reasonable domain for the number of people to attend the show? (Hint: #
Answers
Answer:
don´t ge it sorry
Step-by-step explanation:
a population of women has 40% with dark eyes. if a sample of 20 women are selected from this population, what is the probability that exactly ten of the women have dark eyes?
Answers
The probability that exactly 10 of the 20 women have dark eyes is 0.2051.
What is the probability that exactly ten of the women have dark eyes?The theory used in this question is the binomial probability formula, which is used to calculate the probability of a certain number of successes in a given number of trials.
The steps for this process are as follows
Step 1: Calculate the binomial formula: (n!)/(x!(n-x)!) * p^x * (1-p)^(n-x),
where n is the number of trials (in this case, 20), x is the number of successes (10), p is the probability of a success (0.40 in this case), and n-x is the number of failures (10).
Step 2: Plug the values into the formula: (20!)/(10!(20-10)!) * 0.40^10 * (1-0.40)^(20-10)
Step 3: Simplify the formula: (20*19*18*17*16*15*14*13*12*11) / (10*9*8*7*6*5*4*3*2*1) * 0.40^10 * 0.60^10
Step 4: Calculate the result: 0.2051
To learn more about binomial probability refer :
https://brainly.com/question/29350029
#SPJ4
Right triangle $ABC$ has one leg of length 6 cm, one leg of length 8 cm and a right angle at $A$. A square has one side on the hypotenuse of triangle $ABC$ and a vertex on each of the two legs of triangle $ABC$. What is the length of one side of the square, in cm
Answers
One side of the square has a length of 10 cm.
The triangle $ABC$ is a right triangle and it has one leg of length 6 cm and one leg of length 8 cm. Using the Pythagorean theorem, we can find the length of the hypotenuse:
c^2 = a^2 + b^2
c = √(a^2 + b^2)
c = √(6^2 + 8^2)
c = √(36 + 64)
c = √(100)
c = 10
So the hypotenuse of triangle $ABC$ has a length of 10 cm.
The square has one side on the hypotenuse of the triangle $ABC$ and a vertex on each of the two legs of the triangle $ABC$. Since the square is on the hypotenuse of the triangle, one side of the square has the same length as the hypotenuse of the triangle, which is 10 cm.
Therefore, one side of the square has a length of 10 cm.
To learn more about squares, refer to the link:brainly.com/question/13953405
#SPJ4
Solve for x- round to the nearest tenth- Trigonometry

Answers
Answer:
sin26=11/X
0.438371146789×x=11
X. = 11/0.438371146789
X=25.09289235975
Which of the following values is the 75th percentile?
lower quartile
median
upper quartile
Answers
Answer:
upper quartile
Step-by-step explanation:
upper quartile
