Answers
Answer:
m /CBA = 82 degree
Step-by-step explanation:
if you want explanation tell me
Related Questions
What is/are the increasing interval(s) for the function shown?
Please help !

Answers
When the equation -3x − 5y = -5 is subtracted from -10x + 5y = -60, a third linear equation, -13x = -65, is formed, and it has a different solution from the original equations.
Answers
Answer:
The value of x is 5 and the value of y is -2
Step-by-step explanation:
If the question is to determine the values of x and y, this can be related to the elimination method for solving simultaneous equations.
From the third linear equation, -13x = -65, the value of x can be determined.
-13x = -65
Divide both sides by -13
Then,
-13x/-13 = -65/-13
x = 5
∴ The value of x is 5.
To determine the value of y, the value of x is substituted into any of the first two equations. Say -10x + 5y = -60
-10x + 5y = -60
Substitute x = 5 into the equation
-10(5) + 5y = -60
-50 + 5y = -60
Add 50 to both sides
-50 +50 + 5y = -60 +50
Then,
5y = -10
Divide both sides by 5
5y/5 = -10/5
y = -2
∴ x = 5, y =-2
Hence, the value of x is 5 and the value of y is -2.
Assume a professor gives a 5-question multiple choice quiz where each question has four possible answers (a,b,c,d). How many students must take the quiz to assure that at least two have exactly the same answers to all five questions
Answers
At least 11 students must take the quiz to assure that at least two have exactly the same answers to all five questions.
How to find the students who must take the quiz?Determining the minimum number of students required to guarantee that at least two students have the same answers to all five questions on a multiple choice quiz. Under the area of probability and combinatorics.
There are 4 possible answers for each of the 5 questions, so there are a total of \(4^5 = 1024\) possible sets of answers.
Let's consider the opposite scenario where no two students have exactly the same answers to all five questions. In this case, the first student can choose any of the 1024 possible sets of answers. The second student must choose a different set of answers from the first student, so there are 1023 possible sets of answers for the second student. Similarly, the third student must choose a different set of answers from the first two students, so there are 1022 possible sets of answers for the third student. Continuing in this way, the nth student has 1025-n possible sets of answers to choose from.
Therefore, the total number of possible sets of answers for n students is the product of the number of possible sets of answers for each student:
1024 × 1023 × 1022 × ... × (1025-n)
We want to find the minimum value of n such that this product is less than 1024, because that is the maximum number of sets of answers possible. That is, we want to solve the inequality:
1024 × 1023 × 1022 × ... × (1025-n) < 1024
To simplify this expression, notice that each term in the product is very close to 1024, which suggests that we can approximate the product as \(1024^n\). This approximation is valid when n is much smaller than 1024, which is the case here.
Using this approximation, we can rewrite the inequality as:
\(1024^n\)< 1024
Taking the logarithm base 2 of both sides, we get:
n < log2(1024) = 10
Learn more about probability
brainly.com/question/30034780
#SPJ11
WILL GIVE BRAINLIEST!!!

Answers
Hope this helps
Answer:
A) 115°
Step-by-step explanation:
if PQ || RS then those two angles are supplementary
A rectangle with perimeter 18 cm has a length that is 3 cm more than twice its width. Find the dimensions of the rectangle. SOLVE EACH APPLICATION USING ALGEBRA. TYPE THE EQUATION OR INEQUALITY AND PLEASE SHOW WORK.
Answers
Answer:
Length = 7 cm
Width = 2 cm
Step-by-step explanation:
Perimeter of rectangle = 18 cm
Let length of rectangle = \(l\) cm
Let width of rectangle = \(w\) cm
As per given statement, length is 3 cm more than the twice of its width:
Writing equation:
\(l = 2\times w +3 ....... (1)\)
Formula for perimeter of a rectangle is given as:
\(P = 2 \times (Length + Width)\)
OR
\(P = 2 \times (l + w)\)
Putting values of P as given and \(l\) by using equation (1):
\(18 = 2 \times (2w +3 + w)\\\Rightarrow \dfrac{18}2 = 3w +3 \\\Rightarrow 9 = 3w +3\\\Rightarrow 3w = 9 -3\\\Rightarrow w = \dfrac{6}{3}\\\Rightarrow w = 2\ cm\)
Putting value of \(w\) in equation (1):
\(l = 2\times 2 +3 \\\Rightarrow l = 4+3\\\Rightarrow l = 7\ cm\)
So, the dimensions are:
Length = 7 cm
Width = 2 cm
What is the slope for the equation y = X
+ 5?
Answers
Answer: The slope would be 1.
Step-by-step explanation: The reason why would be because x would have to be assumed as 1. Slope is presented as y=mx+b and while the 1 may not be written there it acts as if "invisible" in the eqaution, as x is the same as writing 1x.
q(x)=-2x-3
r(x)=-x+2
find the value of q(r(5))
Answers
Answer: q(r(5))= 3
Step-by-step explanation: sub in 5 for x in r(x). Once you do that, you'll get -3 for r(5). Now sub in the value of r(5), -3, for x in q(x). Then you'll end up with -9 once the equation has been evaluated.
What is the best classification for -4?
A natural number, whole number
B integer, rational number
C whole number, integer, natural number
D rational number, whole number
NEED HELP ASAP!!!
Answers
-4 is a integer because an integer is a negative number and a natural number, whole number, rational and a irrational number is not a negative number.
PLEASE HELP f(x)=x^2 and g(x)=(x-3)^2+2 Describe how the graph of g(x) relates to the graph of its parent function, f(x). (HINT: Think about how f(x) was shifted to get g(x))
Answers
Answer:
The graph f(x) was shifted 3 units to the right and shifted 2 units up to get the graph of g(x).
Step-by-step explanation:
From the original graph to the transformed one, we can see that the transformations (x - 3) and + 2 were added to the equation.
The (x - 3) means that the x-value of the vertex will increase by 3, meaning that the graph will shift 3 units to the right.
The +2 will increase the y-value of the vertex by 2, meaning that the graph will move up 2 units.
So, the graph of g(x) relates to f(x) as it is a transformation 3 units to the right and 2 units upwards.
Dilbert has p pennies, n nickels, d dimes, and q quarter with a total value of $1. 8. If the numbers p, n, d, and q are distinct and positive, and the greatest common divisor of each pair of these numbers is 1, which is the least possible value of p+n+d+q?
Answers
The least possible value of p+n+d+q would be 6 + 3 + 3 + 3 = 15. So, the least possible value of p+n+d+q is 15.
To solve this problem, we need to use the concept of prime factorization. First, we need to find the least common multiple of the four numbers, p, n, d, and q. To do this, we can factor each of the numbers into their prime factors:
\(p = 2^a * 3^b * 5^c * 7^d \\n = 2^e * 3^f * 5^g * 7^h\\d = 2^i * 3^j * 5^k * 7^l\\q = 2^m * 3^n * 5^o * 7^p\)
The least common multiple (LCM) of p, n, d, and q is the product of the highest power of each prime factor that appears in any of the numbers. For example, the LCM would be 2^i * 3^j * 5^k * 7^l, because that is the highest power of each prime factor that appears in any of the numbers.
Now that we have the LCM of the four numbers, we need to find out how much money that is worth. Since we know that the total value is $1.08, we can divide both sides by the LCM to find out how much each factor is worth:
\(1.08/2^i * 3^j * 5^k * 7^l = x\)
x = 0.01102
So, each factor of the LCM is worth 0.01102. Now, we just need to add up the total number of factors that appear in p, n, d, and q. The least possible value of p+n+d+q would be the sum of the number of powers of each prime factor in p, n, d, and q. For example, if\(p = 2^2 * 3^3 * 5^1 * 7^0, n = 2^1 * 3^2 * 5^0 * 7^2, d = 2^0 * 3^1 * 5^2 * 7^1,\) and \(q = 2^2 * 3^0 * 5^2 * 7^1.\)
Learn more about least common multiple here:
https://brainly.com/question/30060162
#SPJ4
solve the system of equations y=9x+13 y=2x+48 what does the second one equal
Answers
Answer:
x=5 and y=58
Step-by-step explanation:
Someone please help me do this, I don't understand at all and my the teachers that I have are really bad at teaching me things so I'd really appreciate if I had help with this :(

Answers
step 1
Find out the probability that the first spin lands on gray
P=6/(6+2)
P=6/8
step 2
Find out the probability that the second spin lands in blue
P=2/8
therefore
the probability is equal to
P=(6/8)*(2/8)=12/64
simplify
P=6/32=3/16
answer is3/16In P, answer the following:
A. Name a radius
B. Name a diameter
C. Name a cord
D. Name a central angle
E. Name a tangent to the circle

Answers
Answer:
radius=PC
diameter=AB
chord=AC
central angle=angleAPC
tangent=AD
does the math term "mean," mean avarage of most common?
Answers
Answer: The Arithmetic Mean is the average of the numbers: a calculated "central" value of a set of numbers.
Step-by-step explanation: You can find the mean, or average, of a data set in two simple steps: Find the sum of the values by adding them all up. Divide the sum by the number of values in the data set.
name date period portfolio problem: squares and their friends find the area of the shaded square. explain your reasoning. the square below has sides of 2 cm. what is the radius of the circle?
Answers
The area of the shaded square is 4 square centimeters, and the radius of the circle is approximately 1.41 cm.
To find the area of the shaded square and the radius of the circle, we will follow these steps:
Step 1: Identify the dimensions of the square.
From the student question, we know that the square has sides of 2 cm each.
Step 2: Find the area of the square.
The area of a square can be calculated using the formula:
Area = side × side.
In this case, the area of the square is:
2 cm × 2 cm = 4 square centimeters.
Step 3: Find the diagonal of the square.
The diagonal of a square can be found using the Pythagorean theorem:
diagonal² = side² + side².
In this case, the diagonal² = 2 cm² + 2 cm² = 4 cm² + 4 cm² = 8 cm².
Taking the square root of both sides, we get: diagonal = √8 cm ≈ 2.83 cm.
Step 4: Find the radius of the circle.
Since the circle is inscribed in the square, its diameter is equal to the diagonal of the square.
Thus, the radius of the circle is half the diagonal.
Radius = diagonal ÷ 2 ≈ 2.83 cm ÷ 2 ≈ 1.41 cm.
For similar question on circle.
https://brainly.com/question/28162977
#SPJ11
The members of a student council held a car wash to earn money for a field trip. The equations represent how they calculated their earnings.
5c+8v=234
c=2v
If c
represents the number of cars and v
represents the number of vans, which pair of sentences best describe the results of the fundraiser?
Answers
There are 26 automobiles and 13 vans available for the field excursion.
What is equation?An algebraic equation, also known as a polynomial equation, is a mathematical equation of the form P=0, where P is a polynomial with coefficients in some field, most commonly the field of rational numbers. A mathematical statement that expresses the connection between two values is simply characterized as an equation. In an equation, the two values are usually equated by an equal sign. Linear equations are first-order equations. Lines in the coordinate system are determined by linear equations. A linear equation in one variable is defined as an equation with a homogeneous variable of degree 1 (i.e. only one variable). A linear equation can include several variables.
Here,
If c represents the number of cars and v represents the number of vans,
5c+8v=234
c=2v
10v+8v=234
v=234/18
v=13 vans
c=26 cars
The number of cars for field trip is 26 and number of vans is 13.
To know more about equation,
https://brainly.com/question/649785
#SPJ1
A school club is raising money for a trip, and needs to reach $5,000. their fundraising progress is modeled by the equation: t = 350 + 750x, where x is measured in weeks. what is the meaning of the coefficient 750? question 13 options: it is the amount still to be raised. it is the amount they started with. it is the amount they raise each week. it is the amount left over.
Answers
Answer: It is the amount they raise each week
350 is the amount they started with
Solve the equation using multiplication or division.
-7y=28
Oy=-4
Oy = 4
O y = 14
O y = 35
Answers
Answer:
y=-4
Step-by-step explanation:
-7y=28
DIVIDE BY -7
28/-7=-4
Answer=-4
geometry questions please help me
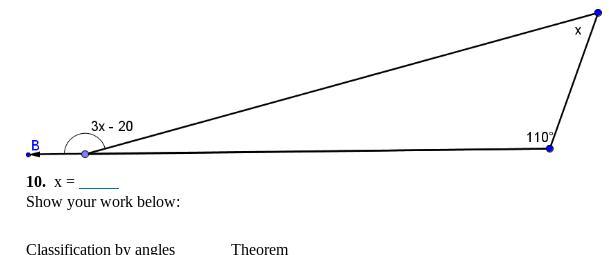
Answers
Answer:
x = 65 degrees
Obtuse Triangle
Step-by-step explanation:
By the Triangle Exterior Angle Theorem, which states that the exterior angle of a triangle is the sum of the two opposite angles:
\(3x - 20 = x + 110\)
Solve for x:
\(3x - x = 110 + 20\\2x = 130\\x = 65\)
So, x = 65 degrees
Because one of the angles are greater than 90 degrees, it is an obtuse triangle.
Mary needs to order pizza for 18 students. Each student should get ¼ of a pizza. How many pizzas should Mary order? How much pizza will be left over?
Answers
Answer:
5 pizzas; 1/2 of a slice
Step-by-step explanation:
18/4=
4.5; the .5 is the leftover as the pizza so Mary needs 5 pizzas to be ordered.
The circle graph shows how Christine's family budgets a total of $76.000 for the year.
Transportation
$6080
Insurance
$4560
Utilities
S2280
Taxes
$ 16,720
Clothing
$5320
Housing
$10,640
Entertainment
59120
Food
$14.440
Savings
56840
Find the percentage of the total budgeted for each category listed below.
Category
Percentage
Answers
The percentage of the total budgeted for each category is as follows: Transportation 8%, Insurance 6%, Utilities 3%, Taxes 22%, Clothing 7%, Housing 14%, Entertainment 1%, Food 19%, Savings 75%.
To calculate the percentage of the total budgeted for each category, we first need to find the total amount budgeted for all categories. Adding up all the amounts given in the graph, we get a total budget of $76,000.
To find the percentage of the budget for each category, we divide the amount budgeted for that category by the total budget and then multiply by 100. For example, for Transportation, we divide $6,080 by $76,000, which gives us 0.08. Multiplying by 100, we get 8%, which is the percentage of the total budget allocated for Transportation. Similarly, we can find the percentage for each category using this method.
Therefore, we can conclude that 8% of the budget is allocated for Transportation, 6% for Insurance, 3% for Utilities, 22% for Taxes, 7% for Clothing, 14% for Housing, 1% for Entertainment, 19% for Food, and 75% for Savings. Understanding how to calculate percentages is an essential skill for budgeting and financial planning.
To learn more about percentage click here, brainly.com/question/29306119
#SPJ11
A yard dart is thrown from a height of 3 feet with an initial velocity of 25 feet per second at an elevation angle of 70°. how long is the dart in the air? round to the nearest tenth. 0.7 seconds 0.8 seconds 1.5 seconds 1.6 seconds
Answers
Based on the height the yard dart is thrown from, the inital velocity, and the elevation angle, the length of time the dart is in the air is 1.6 seconds.
What amount of time did the dart spend in the air?This can be solved using a projectile motion calculator which can show you the velocity of the dart and the time it spent in the air.
Plugging in the given values above, we find that the yard dart spent a total of:
= 1.6 seconds in the air
In conclusion, option D is correct.
Find out more on projectile motion at https://brainly.com/question/24216590.
#SPJ4
I need help IMMEDIATELY!!

Answers
Step-by-step explanation:
Remember SOHCAHTOA
tan(A)=Opposite of Angle A/ Adjacent of Angle A
Sin (B)= Opposite of Angle B/ Hypotenuse
Cos (A)= Adjacent of Angle A/ Hypotenuse
So
\( \tan(a ) = \frac{4}{3} \)
\( \sin(b) = \frac{3}{5} \)
\( \cos( \alpha ) = \frac{3}{5} \)
A running track has two semi-circular ends with radius 31m and two straights of length 92.7m as shown.
Calculate the total area of the track rounded to 1 DP.
Answers
Answer:
Step-by-step explanation:
To find the total area of the track, we need to calculate the area of each section and then add them together.
Area of a semi-circle with radius 31m:
A = (1/2)πr^2
A = (1/2)π(31m)^2
A = 4795.4m^2
Area of a rectangle with length 92.7m and width 31m (the straight parts):
A = lw
A = (92.7m)(31m)
A = 2873.7m^2
To find the total area, we need to add the areas of the two semi-circular ends and the two straight sections:
Total area = 2(Area of semi-circle) + 2(Area of rectangle)
Total area = 2(4795.4m^2) + 2(2873.7m^2)
Total area = 19181.6m^2
Rounding this to 1 decimal place, we get:
Total area ≈ 19181.6 m^2
Therefore, the total area of the track is approximately 19181.6 square meters.
HELP!! I can't figure this out.
Solve for x.
3x =9
Answers
Answer:
The answer is x= 3
Step-by-step explanation:
Divide each term by 3 and simplify.
Hoped this helped!
Could I please get brainly?
A financial analyst wants to set up a hypothesis test to determine if the mean yearly salaries of teachers, tutors, and professors are the same. What would be the correct setup for the null and alternative hypotheses for this test
Answers
Null hypothesis (H0): There’s no effect in the population. Alternative hypothesis (Ha or H1): There’s an effect in the population.
Which null and alternative hypotheses are correct?The null and alternative hypotheses are two opposing ideas that researchers use a statistical test to analyze evidence for and against: The null hypothesis (H0) states that there is no influence in the population. Alternative hypothesis (Ha or H1): There is a population effect.
Identify the null and alternative hypotheses.
As well as the sample size, specify.
Choose a suitable statistical test.
Gather information (note that the previous steps should be done prior to collecting data)
Based on the sample data, compute the test statistic.
Examine the null hypothesis, usually indicated by H0.
Always write the alternative hypothesis, which is usually marked by Ha or H1, with less than, greater than, or not equals symbols, i.e., (,>,or).
To learn more about alternative hypotheses to refer:
https://brainly.com/question/28331914
#SPJ4
The following table shows the results of a coffee taste test given at a local grocery store.
Brand A
Brand B
Total
Men
58
37
95
Women
46
65
111
Total
104
102
206
a) If one of these individuals is selected at random, find the probability that the individual selected prefers Brand
B.
b) If one of these individuals is selected at random, find the probability that the individual selected is a
woman,
given that the person prefers Brand
B.
Question content area bottom
Part 1
a) The probability
that
the individual selected prefers Brand
B
is
enter your response here.
(Type an integer or a simplified fraction.)
Answers
The required answer is R_0 = inf{|z - z_0|: f(z) non-analytic or undefined at z}.
Explanation:
If |z - z_0| < R_0, then f(z) is analytic at z.
We know that the power series Σ a_n (z – z_0)^n has a radius of convergence R_0. This means that the series converges absolutely for |z - z_0| < R_0 and diverges for |z - z_0| > R_0.
Now, for any point z within the radius of convergence, we can write f(z) as the sum of the power series:
f(z) = Σ a_n (z – z_0)^n
Since the power series converges absolutely for |z - z_0| < R_0, we can differentiate the series term by term. The resulting series will also converge absolutely within the radius of convergence, giving us the derivative of f(z) as:
f'(z) = Σ (n * a_n) (z – z_0)^(n-1)
By repeating this process, we can differentiate f(z) infinitely many times within the radius of convergence, showing that f(z) is analytic at z for |z - z_0| < R_0.
If |z - z_0| > R_0, then f(z) is either non-analytic or undefined at z.
Let's assume that |z - z_0| > R_0. Since the power series has a radius of convergence R_0, it means that the series diverges for |z - z_0| > R_0.
If f(z) were analytic at z, we could express it as a power series centered at z:
f(z) = Σ b_n (z - z_0)^n
However, since the power series of f(z) has a radius of convergence R_0 and the distance from z_0 to z is greater than R_0, this would contradict the definition of the radius of convergence.
Therefore, if |z - z_0| > R_0, f(z) cannot be expressed as a power series and is either non-analytic or undefined at z.
Combining both statements, we have shown that R_0 = inf{|z - z_0|: f(z) non-analytic or undefined at z}, which concludes the proof.
To know about radius of convergence. To click the link
https://brainly.com/question/31440916.
#SPJ11
The required answer is \(R_0 = inf{|z - z_0|:\) f(z) non-analytic or undefined at z through radius of convergence.
Explanation:
If \(|z - z_0| < R_0,\) then f(z) is analytic at z.
We know that the power series Σ \(a_n (z- z_0)^n\) has a radius of convergence \(R_0.\) This means that the series converges absolutely for \(|z - z_0| < R_0\) and diverges for \(|z - z_0| > R_0.\)
Now, for any point z within the radius of convergence, we can write f(z) as the sum of the power series:
f(z) = Σ \(a_n (z -z_0)^n\)
Since the power series converges absolutely for |z - z_0| < R_0, we can differentiate the series term by term. The resulting series will also converge absolutely within the radius of convergence, giving us the derivative of f(z) as:
f'(z) = Σ \((n * a_n) (z -z_0)^(n-1)\)
By repeating this process, we can differentiate f(z) infinitely many times within the radius of convergence, showing that f(z) is analytic at z for \(|z - z_0| < R_0.\)
If \(|z - z_0| > R_0,\) then f(z) is either non-analytic or undefined at z.
Let's assume that \(|z - z_0| > R_0.\) Since the power series has a radius of convergence R_0, it means that the series diverges for \(|z - z_0| > R_0.\)
If f(z) were analytic at z, we could express it as a power series centered at z:
f(z) = Σ \(b_n (z - z_0)^n\)
However, since the power series of f(z) has a radius of convergence \(R_0\) and the distance from \(z_0\) to z is greater than R_0, this would contradict the definition of the radius of convergence.
Therefore, if \(|z - z_0| > R_0,\) f(z) cannot be expressed as a power series and is either non-analytic or undefined at z.
Combining both statements, we have shown that \(R_0 = inf{|z - z_0|:\) f(z) non-analytic or undefined at z, which concludes the proof.
To know about radius of convergence. To click the link
brainly.com/question/31440916.
#SPJ4
Identify the similar triangles. Find x and the measures of the indicated sides.
What is the answer? Angle similarity

Answers
Answer:
See belowStep-by-step explanation:
Given:
Angles A and C are equal. This makes triangles similar:
ΔAED ~ ΔCBDRatio of corresponding sides is same:
AE/BC = DE/BD(x + 1)/(x + 5) = 2.4/7.23(x + 1) = x + 53x + 3 = x + 52x = 2x = 1Side measures are:
DE = 1 + 1 = 2BD = 1 + 5 = 6Trevon and Ashley are selling cookie dough for a school fundraiser. Customers can buy packages of chocolate chip cookie dough and packages of gingerbread cookie dough. Trevon sold 6 packages of chocolate chip cookie dough and 2 packages of gingerbread cookie dough for a total of $72. Ashley sold 6 packages of chocolate chip cookie and 10 packages or gingerbread cookie dough for a total of $216. What is the cost if each of one package of chocolate chip cookie dough and one package of gingerbread cookie dough
Answers
Answer:
the cost of one package of chocolate chip cookie and one package of ginger bread is $6 and $18 respectively
Step-by-step explanation:
The computation of the cost of one package of chocolate chip cookie and one package of ginger bread is shown below:
Let us assume the package of chocolate chip cookie be x
And, the package of ginger bread is y
So,
According to the question
6x + 2y = $72
6x + 10y = $216
Now subtract equation 1 from equation 2
-8y = -144
y = $18
And, for x it would be
6x + $36 = $72
x = $6
Hence, the cost of one package of chocolate chip cookie and one package of ginger bread is $6 and $18 respectively
solve this please and tell me how you did it
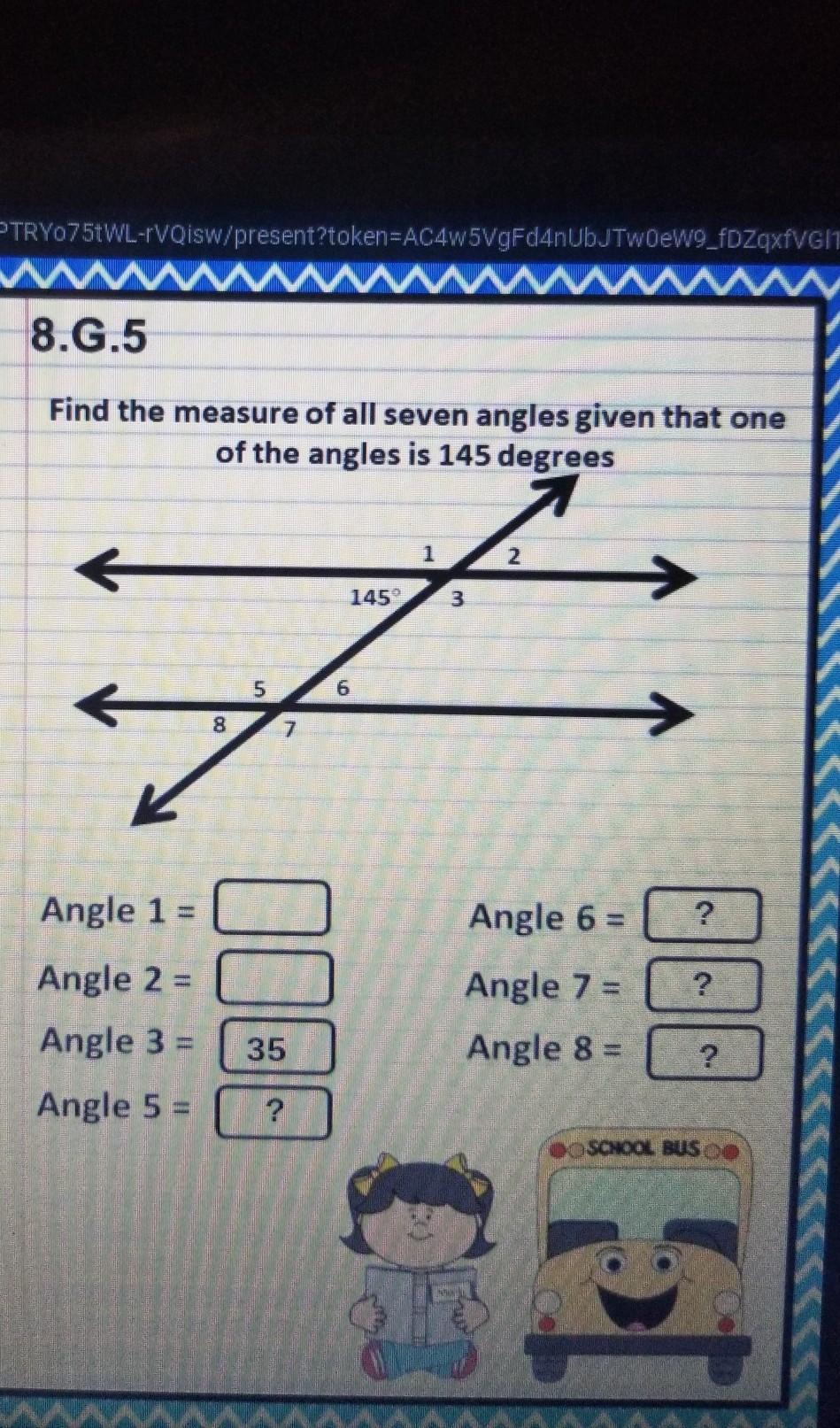
Answers
The angle ∠2 is a vertically opposite angle to the angle 145°, so they are congruent:
∠2 = 145°
The angles 1 and 3 are supplementary angles to the angle 145°, so they are equal to:
180° - 145° = 35°
∠1 = 35°
∠3 = 35°
The angle 8 is a corresponding angle to the angle 145°, so they are congruent:
∠8 = 145°
The angle ∠6 is a vertically opposite angle to the angle ∠8 so they are congruent:
∠6 = 145°
The angles 5 and 7 are supplementary angles to the angle ∠8, so they are equal to:
180° - 145° = 35°
∠5 = 35°
∠7 = 35°
