can someone please help me with this question
​

Answer:

cos57° = x/51

General Formulas and Concepts:

Trigonometry

Step-by-step explanation:

Step 1: Define

We are given a right triangle. We can use trig to solve for the missing side length.

Step 2: Set up ratios

We can choose between the 2 angles and have multiple ratios to solve for x.

sin33° = x/51

cos57° = x/51

Hence, we see that the 1st option would be the correct answer.

There are 29.8 students in the running club overall.

The quotient is the number we get when we divide two numbers. For instance, in the case of 8 4 = 2, where the division result is 2, it is the quotient. The divisor is 4, and the dividend is 8.

The remnant is the amount that does not wholly enter the divisor, whereas the quotient is the number of times a division is completed to the fullest extent possible. By way of illustration, 42 is the quotient and 1 is the remainder when 127 is divided by 3 to provide 42 R 1.

Given,

30+9-46 (2/3) % × 30

Multiply

30 + 9 - (46 × 30) × 0.00666666666666667

Calculate quotient,

30 + 9 - 1380 × 0.00666666666666667

Simplifying quotient,

30 + 9 - 9.2

Then we get,

39 - 9.2

Then 29.8

get the result: 29.8

The complete question is:

Thirty 8 th  graders signed up for running club, however nine dropped out before the first practice. If 46 (2/3)  of the club are 8 th graders, how many total students are in the running club?

To learn more about quotient, refer to:

https://brainly.com/question/11995925

#SPJ4

The total amount of money that will be available after 25 years is $191,727.98 and the total amount of deposits made over the time period is much less than the amount of money that will be available after 25 years.

Given that you put $422 per month in an investment plan that pays an APR of 3%.

We need to calculate how much money you will have after 25 years and compare this amount to the total amount of deposits made over the time period.

To find out the total amount of money that will be available after 25 years, we will use the formula for future value of an annuity.

FV = PMT * (((1 + r)n - 1) / r)

where,FV is the future value of annuity PMT is the payment per period n is the interest rate per period n is the total number of periodsIn this case,

PMT = $422r = 3% / 12 (monthly rate) = 0.25%n = 25 years * 12 months/year = 300 months.

Now, let's substitute the values in the formula,

FV = $422 * (((1 + 0.03/12)300 - 1) / (0.03/12))= $422 * (1.1378 / 0.0025)= $191,727.98.

Therefore, the total amount of money that will be available after 25 years is $191,727.98.

Now, let's calculate the total amount of deposits made over the time period.

Total deposits = PMT * n= $422 * 300= $126,600.

Comparing the two amounts, we can see that the total amount of deposits made over the time period is much less than the amount of money that will be available after 25 years.Therefore,investing in an annuity with a 3% APR is a good investment option.

To know more about amount click here:

https://brainly.com/question/32453941

#SPJ11

The domain of the function g(x) = \(sin^-1(2x + 4)\) is [-5/2, -3/2] in interval notation. The range of the function g(x) = \(sin^-1(2x + 4)\) is [-π/2, π/2] in interval notation.

The given function is g(x) = \(sin^-1(2x + 4)\).

To find the domain of the function, we need to determine the set of all possible input values (x) for which the function is defined.

The inverse sine function, \(sin^-1(x)\), is defined for values of x in the interval [-1, 1].

So, in order for g(x) = \(sin^-1(2x + 4)\) to be defined, we need to satisfy the condition -1 ≤ 2x + 4 ≤ 1.

Solving this inequality:

-1 ≤ 2x + 4 ≤ 1

-5 ≤ 2x ≤ -3

-5/2 ≤ x ≤ -3/2

Therefore, the domain of the function g(x) = \(sin^-1(2x + 4)\) is [-5/2, -3/2] in interval notation.

To find the range of the function, we need to determine the set of all possible output values (g(x)).

The range of the inverse sine function, \(sin^-1(x)\), is [-π/2, π/2], which means that the output values of g(x) will fall within this interval.

Therefore, the range of the function g(x) = \(sin^-1(2x + 4)\)is [-π/2, π/2] in interval notation.

To learn more about the domain visit:

brainly.com/question/13109733

#SPJ11

The complete question is:<Find the domain and range of the following function. (Enter your answers in interval notation.) g(x) = \(sin^-1(2x + 4)\) domain [-5/2, -3/2] range [-pi/2, pi/2]>

Answer:

3 17/30

Step-by-step explanation:

In order to do this problem, we have to get the two fractions to have the same denominator

So we change 2 8/15 into 2 16/30 (multiplying both the numerator by 2, if you don't know why this works then ask me) and then we just add. So 2 16/30 + 1 1/30 = 3 17/30

Answer:

Let's use a starting pay of 2,000.

2,000 × 10%= 200

2,000 + 200= 2,200

2,200 × 10%= 220

2,200 +220 =2,420

Now lets take 2,000 ×20%= 400

2,000+400= 2,400

Answer:

The width is 9 cm

Step-by-step explanation:

L(W)(H) = V

35(W)(36) = 11340

Solve for w

35w(36) - 11340

1260w=11340

divide both sides by 1260 to get 9

Answer:

60,000 cm3

Step-by-step explanation:

cool right

The coordinates of the vertices of the image of the square are S'(x, y) = (- 1, - 4), T'(x, y) = (- 1, 1), U'(x, y) = (4, 1) and V'(x, y) = (4, - 4).

In this problem we need to make use of a translation on a geometric locus on a Cartesian plane, which is generated by four points representing the vertices of the square. The translation is a kind of rigid transformation, whose formula is shown below:

P'(x, y) = P(x, y) + t(x, y)

Where:

If we know that S(x, y) = (- 6, - 5), T(x, y) = (- 6, 0), U(x, y) = (- 1, 0) and V(x, y) = (- 1, - 5) and t(x, y) = (5, 1), then the locations of the vertices of the triangle are:

S'(x, y) = (- 6, - 5) + (5, 1)

S'(x, y) = (- 1, - 4)

T'(x, y) = (- 6, 0) + (5, 1)

T'(x, y) = (- 1, 1)

U'(x, y) = (- 1, 0) + (5, 1)

U'(x, y) = (4, 1)

V'(x, y) = (- 1, - 5) + (5, 1)

V'(x, y) = (4, - 4)

The location of the image of the square is shown below.

To learn more on translations: https://brainly.com/question/12463306

#SPJ1

Answer:

The solution I got is (4,2)

Step-by-step explanation:

When I plotted the equations on a graph, they intercepted at (4,2).

A. Using the distance formula, we can state that the opposite sides are congruent because AD = BC = √10 units and AB = CD = √40 units.

B. The diagonals are equal, AC = BD = √50 units.

C. Based on the slopes of each side, there are 4 right angles on the rectangle.

The distance formula is used to find the distance that exist between tow points that are on a coordinate plane. The formula is: d = \(\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\).

What is the Slope of a Line?

Slope = change in y / change in x.

A. The coordinates of each of the vertices of the rectangle are:

A(1, 2)

B(7, 4)

C(8, 1)

D(2, -1)

Use the distance formula to find AB, CD, BC, and AD.

AB = √[(7−1)² + (4−2)²]

AB = √40

CD = √[(2−8)² + (−1−1)²]

CD = √40

BC = √[(8−7)² + (1−4)²]

BC = √10

AD = √[(2−1)² + (−1−2)²]

AD = √10

Therefore, the opposite sides are congruent because AD = BC = √10 units and AB = CD = √40 units.

B. The diagonals are AC and BD. Find their lengths using the distance formula:

AC = √(8−1)² + (1−2)²]

AC = √50 units

BD = √[(2−7)² + (−1−4)²]

BD = √50 units

Therefore, the diagonals are equal, AC = BD = √50 units.

C. Find the slope of AB, CD, BC, and AD:

Slope of AB = change in y / change in x = rise/run = 2/6 = 1/3

Slope of CD = 2/6 = 1/3

Slope of BC = -3/1 = -3

Slope of AD = -3/1 = -3

-3 is the negative reciprocal to 1/3, this means that, if the two lines that meet at a corner have these two slope, then they will form a right angle because they are perpendicular to each other.

Therefore, there are 4 right angles on the rectangle.

Learn more about the distance formula on:

https://brainly.com/question/661229

#SPJ1

Given ages represent the consecutive integers  and sum of  Scarlett's age and five times Nasim age is 185 , then Scarlett age is equal to 30 years.

As given in the question,

Age represents the consecutive integers and Scarlett age is less than Nasim's age.

Let 'x' represent the age of Scarlett

And ' x + 1' represents the age of Nasim

As per the given condition of their ages we have,

x + 5 ( x + 1 ) = 185

⇒ x + 5x + 5 = 185

⇒ 6x + 5 = 185

⇒ 6x = 185 - 5

⇒ 6x = 180

⇒ x = 180 / 6

⇒ x = 30 years

Therefore, for the given ages represent the consecutive integers  and sum of  Scarlett's age and five times Nasim age is 185 , then Scarlett age is equal to 30 years.

Learn more about consecutive integers here

brainly.com/question/1767889

#SPJ4

The factorization of the given expression \(\rm x^2+10x+21\) is (x+3)(x+7) the option first is correct.

It is given that the expression \(\rm x^2+10x+21\)

It is required to find which expression is the factorization of the given expression, the options are:

a) (x + 3)(x + 7)

b) (x + 4)(x + 6)

c) (x + 6)(x + 15)

d) (x + 7)(x + 14)

Polynomial is the combination of variables and constants in a systematic manner with "n" number of power in ascending or descending order.

We have an expression:

\(\rm x^2+10x+21\)

\(\rm x^2+7x+3x+21\)  

Breaking 10x into 7x and 3x because the multiplication of 7x and 3x is \(\rm 21x^2\) and the addition is 10x.

\(\rm x^2+7x+3x+21\\\\\rm x(x+7)+3(x+7)\\\\\rm (x+7)(x+3)\)or

\(\rm (x+3)(x+7)\)

Thus, the factorization of the given expression \(\rm x^2+10x+21\) is (x+3)(x+7) the option first is correct.

Learn more about Polynomial here:

brainly.com/question/17822016

The measures represent a 7-point Likert scale.

Interval scales are numerical scales in which the difference between any two adjacent points is the same.

Examples of interval scales include temperature (in Celsius or Fahrenheit), standard IQ scores, and dates.

Ordinal scales are numerical scales in which the difference between any two adjacent points is not necessarily the same.

Examples of ordinal scales include rankings (e.g., 1st, 2nd, 3rd, etc.), letter grades (A, B, C, etc.), and Likert scales (e.g., strongly agree, agree, neutral, disagree, strongly disagree).

Ordinal scales allow for the ranking of items, but the distances between points on the scale are not necessarily equal.

Interval scales, on the other hand, measure the distance between points on the scale and the difference between any two points is the same.

For similar question on measures:

https://brainly.com/question/25169033

#SPJ11

First, we want to note two things:

We can describe this with an inequality:  x ≥ -10
Be sure you use ≥ and not >, since -10 is included.

We can describe this with interval notation: [ -10, infty )
Be sure you use [ and not ( on -10, since -10 is included.

You can also use set-builder notation: { x | x ≥ -10 }

Answer:

5/2

Step-by-step explanation:

25 and 10 so 25/10 or 5/2 or 2 1/2

Answer:

x = 6\(\sqrt{5}\)

Step-by-step explanation:

Here we need to use the Pythagorean Theorem

Pythagorean Theorem: a^2 + b^2 = c^2

STEP 1: Define your variables

The legs of the triangle are a and b, and the hypotenuse is c.

a = x

b = 4

c = 14

STEP 2: Plug your variables into the equation and solve

x^2 + 4^2 = 14^2

x^2 + 16 = 196

x^2 + 16 - 16 = 196 - 16

x^2 = 180

\(\sqrt{x^2}\) = \(\sqrt{180}\)

STEP 3: Simplify

Since the question asks you to put the equation in simplified radical form, you do not have to approximate the answer, but you do have to simplify the radical.

\(\sqrt{x^2}\) = \(\sqrt{180}\)

x = \(\sqrt{36}\) * \(\sqrt{5}\)

x = 6\(\sqrt{5}\)

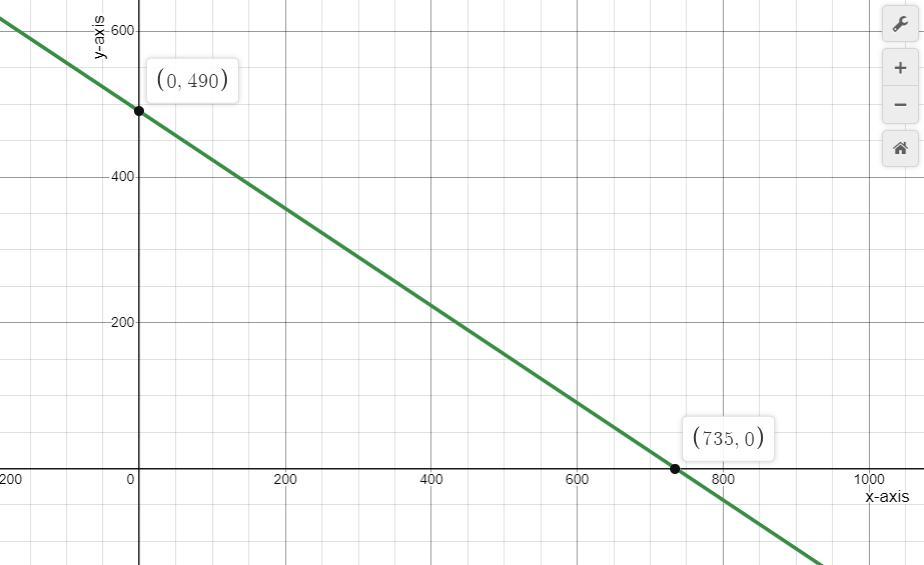
1. The equation to slope-intercept form is y = -2/3(x) + 490. The slope is -2/3 and the y-intercept is 490.

2. You should start at the y-intercept (0, 490) and move right by 3 units and downward by 2 units, and then connect the points.

3. The equation in function notation is f(x) = -2/3(x) + 490. The graph of the function is the rate of change with respect to the number of sandwich lunch sold.

4. A graph of the function with intercepts is shown below.

5. The graphs of the functions for the two months both have the same slope but different y-intercept and x-intercept.

In Mathematics and Geometry, the slope-intercept form of the equation of a straight line is given by this mathematical equation;

y = mx + b

Where:

Based on the information provided above, a linear equation that models Sal's Sandwich Shop's profit is given by;

2x + 3y = 1,470

By subtracting 2x from both sides of the equation and dividing by 3, we have:

2x + 3y - 2x = 1,470 - 2x

y = -2/3(x) + 490

Therefore, the slope is -2/3 and the y-intercept is 490.

Part 2.

In order to graph the equation by using the slope-intercept method, you would start at the y-intercept (0, 490) and move right by 3 units and down by 2 units, and then connect the points.

Part 3.

Next, we would write the equation in function notation as follows;

f(x) = -2/3(x) + 490

where:

The graph represents the rate of change of the function with respect to the number of sandwich lunch sold.

Part 4.

In this context, we would use an online graphing calculator to plot the linear function as shown in the image attached below.

Part 5.

Assuming Sal's total profit on lunch specials for the next month is $1,593 and the profit amounts remain the same, a system of equations to model this situation is given by:

2x + 3y = 1593; y = -2/3(x) + 531.

2x + 3y = 1,470; y = -2/3(x) + 490.

In conclusion, we can logically deduce that the graphs of the functions for the two months both have the same slope but different y-intercept and x-intercept.

Read more on slope-intercept here: brainly.com/question/7889446

#SPJ1

Complete Question:

Sal's Sandwich Shop sells wraps and sandwiches as part of its lunch specials. The profit on every sandwich is $2, and the profit on every wrap is $3. Sal made a profit of $1,470 from lunch specials last month. The equation 2x + 3y = 1,470 represents Sal's profits last month, where x is the number of sandwich lunch specials sold and y is the number of wrap lunch specials sold.

Answer:

54:78

Step-by-step explanation:

We multiply 9 and 13 to 6

9 × 6 = 54

13 × 6 = 78

54 + 78 = 132

Ratio representation gives the sharing proportion of a number, the numbers expressed in the ratio 9:13 of 132 are 54 and 78 respectively

Given the Parameters :

To obtain each Value, we use the relation ;

For the 9 portion of the ratio :

(9 / (9+ 13)) × 132

(9 / 22) × 132

= 54

For the 13 portion of the ratio :

(13 / (9+ 13)) × 132

(13 / 22) × 132

= 78

Therefore, the two numbers are 54 and 78

Learn more : https://brainly.com/question/18109354

The time traveler explained that time travel was possible by utilizing a time machine that allowed him to manipulate the fabric of space-time.

"The Time Machine" by H.G. Wells, the Time Traveler explains that time travel is possible by using a device he invented called the Time Machine. He describes the concept of the fourth dimension, suggesting that time is like a spatial dimension that can be traversed.
The Time Traveller's experimental verification involves him actually using the Time Machine to travel into the future. He shares his experiences of traveling to the year 802,701 AD, where he encounters two different species: the Eloi and the Morlocks. He provides vivid descriptions of the future society and the physical changes that have occurred over time.
By sharing his personal experiences and observations from his journey, the Time Traveller provides experimental evidence for the possibility of time travel.

To know more about observations visit:

https://brainly.com/question/9679245
#SPJ11

Answer:

MP=(6,8)

Step-by-step explanation:

\(MP= (\frac{x_1+x_2}{2} )(\frac{y_1+y_2}{2} )\\MP= (\frac{9+3}{2} )(\frac{7+9}{2})\\MP= (\frac{12}{2} )(\frac{16}{2} )\\MP= (6,8)\)

The median of all these numbers in dollars is 7.5.

When the no. of given data are odd we arrange those nos. in an order increasing or decreasing order and the middle no. is the median of the given odd numbers.

According to the given question the following values represent the amount of money (in dollars) 10 people have in their wallets: 10, 12, 19, 5, 6, 8, 1, 13, 4, 7 and we have to find the median.

First we observe that no. of people is even so there will be two middle nos.

Now lets arrange these nos. in an order from least to greatest which is

1, 4, 5, 6, 7, 8, 10, 12, 13, 19 in this 7 and 8 are middle numbers.

So, to find the median of all these nos. we will divide these two middle nos. by 2.

∴  ( 7 + 8 )/2

= 15/2

= 7.5.

Learn more about median here :

https://brainly.com/question/28060453

#SPJ4

the equation of the line can be written in slope-intercept form as

To get the equation of the line, solve for the value of m and b.

Based on the given plot, the first point (lower point) has the coordinates (-3,-3) while the second point (higher point) has the coordinates (3, 5). We need these to solve for the slope of the line. The slope of the line can be computed using the equation

Substitute the values on the equation above based on the coordinates of the two points and compute

What's left to solve is the value of b. To solve this, use one of the coordinates and input the values on the slope-intercept form of the equation of the line along with the value of m, In this case, I will be using (3, 5). We have

We now have the values for m and b. Just put it on the slope-intercept line form to represent the equation of the line

Answer: y = (4/3)x + 1

The population of New York City in 2013, which is approximately 8,406,000 people, can be approximated as 8.4 million. This represents a single digit (8) multiplied by a power of 10 (million).

When we approximate the population of New York City as 8.4 million, we are expressing the number in scientific notation, where the single digit is 8 and the power of 10 is 6 (million).

In scientific notation, a number is written as a decimal coefficient multiplied by a power of 10. The coefficient is typically chosen to be a single digit, which in this case is 8. The power of 10 represents the number of zeros that follow the coefficient, and in this case, it is 6 because we have "million," which corresponds to 6 zeros.

By approximating the population as 8.4 million, we are representing it as a single digit (8) multiplied by a power of 10 (million), which fulfills the criteria of being a population approximated as a single digit times a power of 10.

Learn more about power here:

https://brainly.com/question/13303295

#SPJ11

The complete question is:

The population of new york city in 2013 was about 8,406,000 people. which number best approximates the population as a single digit times a power of 10?

Answer:

37

Step-by-step explanation:

k(x) = 4x2 + 1

\( = 4( - 3) {}^{2} + 1 \\ 4(9) + 1 \\ 36 + 1 \\ 37\)

Given:

An exterior angle of a triangle = 2x+30°

Two opposite interior angles are 33° and 41°.

To find:

The value of x.

Solution:

According to the exterior angle thereom, the exterior angle of a triangle is equal to the sum of opposite interior angles.

Using exterior angle theroem, we get

\((2x+30)^\circ=33^\circ+41^\circ\)

\((2x+30)^\circ=74^\circ\)

\((2x+30)=74\)

On further simplification, we get

\(2x=74-30\)

\(2x=44\)

\(x=\dfrac{44}{2}\)

\(x=22\)

Therefore, the value of x is 22.

Answer:  Marty would receive $69.00.

Step-by-step explanation:

15% is 9 of 60.

Answer:

3,5 .4,4.6,8.

Step-by-step explanation:

tfjfkggkhhkjgiifkgftthvgyybf

a) X is an unbiased estimator of p. b) The Var(X) is p(1-p)/n. c) The E[X(1-X)] is (n-1)[p(1-p)/n]. d) The value of c is c = 1/(n-1).

(a) To show that X = Y/n is an unbiased estimator of p, we need to show that E[X] = p.

Since Y is a sum of n iid Bern(p) random variables, we have E[Y] = np.

Now, let's find the expected value of X:

E[X] = E[Y/n] = E[Y]/n = np/n = p.

Therefore, X is an unbiased estimator of p.

(b) To find the variance of X, we'll use the fact that Var(aX) = a^2 * Var(X) for any constant a.

Var(X) = Var(Y/n) = Var(Y)/n² = np(1-p)/n² = p(1-p)/n.

(c) To show that E[X(1-X)] = (n-1)[p(1-p)/n], we expand the expression:

E[X(1-X)] = E[X - X²] = E[X] - E[X²].

We already know that E[X] = p from part (a).

Now, let's find E[X²]:

E[X²] = E[(Y/n)²] = E[(Y²)/n²] = Var(Y)/n² + (E[Y]/n)².

Using the formula for the variance of a binomial distribution, Var(Y) = np(1-p), we have:

E[X²] = np(1-p)/n² + (np/n)² = p(1-p)/n + p² = p(1-p)/n + p(1-p) = (1-p)(p + p(1-p))/n = (1-p)(p + p - p²)/n = (1-p)(2p - p²)/n = 2p(1-p)/n - p²(1-p)/n = 2p(1-p)/n - p(1-p)²/n = [2p(1-p) - p(1-p)²]/n = [p(1-p)(2 - (1-p))]/n = [p(1-p)(1+p)]/n = p(1-p)(1+p)/n = p(1-p)/n.

Therefore, E[X(1-X)] = E[X] - E[X²] = p - p(1-p)/n = (n-1)p(1-p)/n = (n-1)[p(1-p)/n].

(d) To find the value of c such that cX(1-X) is an unbiased estimator of p(1-p)/n, we need to have E[cX(1-X)] = p(1-p)/n.

E[cX(1-X)] = cE[X(1-X)] = c[(n-1)[p(1-p)/n]].

For unbiasedness, we want this to be equal to p(1-p)/n:

c[(n-1)[p(1-p)/n]] = p(1-p)/n.

Simplifying, we have:

c(n-1)p(1-p) = p(1-p).

Since this should hold for all values of p, (n-1)c = 1.

Therefore, the value of c is c = 1/(n-1).

To know more about unbiased estimator:

https://brainly.com/question/32063886

#SPJ4

Based on the formula of the quadratic function y=-x^2+6x-5, we know that its graph is a downward-facing parabola that opens wide, with a vertex at (3,-14), and an axis of symmetry at x=3.

Based on the formula of the quadratic function y=-x^2+6x-5, we can determine several properties of its graph, including its shape, vertex, and axis of symmetry.

First, the negative coefficient of the x-squared term (-1) tells us that the graph will be a downward-facing parabola. The leading coefficient also tells us whether the parabola is narrow or wide. Since the coefficient is -1, the parabola will be wide.

Next, we can find the vertex using the formula:

Vertex = (-b/2a, f(-b/2a))

where a is the coefficient of the x-squared term, b is the coefficient of the x term, and f(x) is the quadratic function. Plugging in the values for our function, we get:

Vertex = (-b/2a, f(-b/2a))

= (-6/(2*-1), f(6/(2*-1)))

= (3, -14)

So the vertex of the parabola is at the point (3,-14).

Finally, we know that the axis of symmetry is a vertical line passing through the vertex. In this case, it is the line x=3.

Know more about quadratic function here;

https://brainly.com/question/18958913

#SPJ11