Answers
Answer:
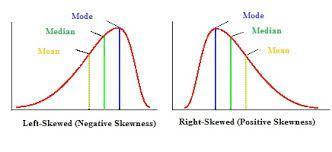
so for the mean u add all the numbers on there and then divide it by 5 since there are 5 numbers on there so 78+84+100+78+81=421 now we divide 421 by 5 so 421÷5= 84!
now the median would be 100? and the mode is 78 since 78 is the number that showed the most!
Median = 100
Mode= 78
Related Questions
Write an equation for the function graphed

Answers
The equation for the function graphed above is g(x) = |x-2 | + 1.
What is Function?In mathematics, a function is represented as a rule that produces a distinct result for each input x. The collection of all the values that the function may input while it is defined is known as the domain. The entire set of values that the function's output can produce is referred to as the range. The set of values that could be a function's outputs is known as the co-domain.
Given:
We have the Function f(x) = |x|.
Here the expression of g(x) is the consequence of translating both horizontally and vertically regarding f(x), which it can be defined as
g(x) = f(x-h)+ k
where (h, k) Coordinates of the "center" of the resulting function.
From graph we have (h, k)= (2, 1) and f(x) = |x| then the resulting function is
g(x) = |x-2 | + 1
Learn more about function here:
https://brainly.com/question/22775707
#SPJ1
Consider a medium with parameters € = 1.2 (10^-10 )F/m , n= 3(10^-3) H/m and sigma=0. Magnetic field intensity in the medium is given as R = 2cos (10^10t- 600x)äz Am.
Use Maxwell's equations to obtain the followings:
1) Magnetic flux density
These questions is circuit theory
Answers
Using Maxwell's equations, we can determine the magnetic flux density. One of the Maxwell's equations is:
\(\displaystyle \nabla \times \mathbf{H} = \mathbf{J} + \frac{\partial \mathbf{D}}{\partial t}\),
where \(\displaystyle \nabla \times \mathbf{H}\) is the curl of the magnetic field intensity \(\displaystyle \mathbf{H}\), \(\displaystyle \mathbf{J}\) is the current density, and \(\displaystyle \frac{\partial \mathbf{D}}{\partial t}\) is the time derivative of the electric displacement \(\displaystyle \mathbf{D}\).
In this problem, there is no current density (\(\displaystyle \mathbf{J} =0\)) and no time-varying electric displacement (\(\displaystyle \frac{\partial \mathbf{D}}{\partial t} =0\)). Therefore, the equation simplifies to:
\(\displaystyle \nabla \times \mathbf{H} =0\).
Taking the curl of the given magnetic field intensity \(\displaystyle \mathbf{R} =2\cos( 10^{10} t-600x)\hat{a}_{z}\, \text{Am}\):
\(\displaystyle \nabla \times \mathbf{R} =\nabla \times ( 2\cos( 10^{10} t-600x)\hat{a}_{z}) \, \text{Am}\).
Using the curl identity and applying the chain rule, we can expand the expression:
\(\displaystyle \nabla \times \mathbf{R} =\left( \frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial y} -\frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial z}\right) \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Since the magnetic field intensity \(\displaystyle \mathbf{R}\) is not dependent on \(\displaystyle y\) or \(\displaystyle z\), the partial derivatives with respect to \(\displaystyle y\) and \(\displaystyle z\) are zero. Therefore, the expression further simplifies to:
\(\displaystyle \nabla \times \mathbf{R} =-\frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial x} \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Differentiating the cosine function with respect to \(\displaystyle x\):
\(\displaystyle \nabla \times \mathbf{R} =-2( 10^{10}) \sin( 10^{10} t-600x)\hat{a}_{z} \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Setting this expression equal to zero according to \(\displaystyle \nabla \times \mathbf{H} =0\):
\(\displaystyle -2( 10^{10}) \sin( 10^{10} t-600x)\hat{a}_{z} \mathrm{d} x\mathrm{d} y\mathrm{d} z =0\).
Since the equation should hold for any arbitrary values of \(\displaystyle \mathrm{d} x\), \(\displaystyle \mathrm{d} y\), and \(\displaystyle \mathrm{d} z\), we can equate the coefficient of each term to zero:
\(\displaystyle -2( 10^{10}) \sin( 10^{10} t-600x) =0\).
Simplifying the equation:
\(\displaystyle \sin( 10^{10} t-600x) =0\).
The sine function is equal to zero at certain values of \(\displaystyle ( 10^{10} t-600x) \):
\(\displaystyle 10^{10} t-600x =n\pi\),
where \(\displaystyle n\) is an integer. Rearranging the equation:
\(\displaystyle x =\frac{ 10^{10} t-n\pi }{600}\).
The equation provides a relationship between \(\displaystyle x\) and \(\displaystyle t\), indicating that the magnetic field intensity is constant along lines of constant \(\displaystyle x\) and \(\displaystyle t\). Therefore, the magnetic field intensity is uniform in the given medium.
Since the magnetic flux density \(\displaystyle B\) is related to the magnetic field intensity \(\displaystyle H\) through the equation \(\displaystyle B =\mu H\), where \(\displaystyle \mu\) is the permeability of the medium, we can conclude that the magnetic flux density is also uniform in the medium.
Thus, the correct expression for the magnetic flux density in the given medium is:
\(\displaystyle B =6\cos( 10^{10} t-600x)\hat{a}_{z}\).
Could someone help me solve this? TIA

Answers
The exact value of the specified trigonometric identity found using the the trigonometric identity for tan(A - B) and tan(arccos(x)) and tanarcsin(x)) is presented as follows;
\(tan\left(sin^{-1}\left(\dfrac{3}{4} \right) - cos^{-1}\left(\dfrac{1}{5}\right) \right) =\dfrac{32\cdot \sqrt{6}- 75\cdot \sqrt{7} }{209}\)
What is a trigonometric identity?A trigonometric identity is an equality that involves trigonometric functions that is valid for all values of the arguments of the equation
The required trigonometric identities are;
\(tan (A - B) = \dfrac{tan(A) -tan(B)}{1-tan(A)\cdot tan(B)}\)
\(tan(sin^{-1}(x)) = \dfrac{x}{\sqrt{1-x^2} }\)
\(tan(cos^{-1}(x)) = \dfrac{\sqrt{1-x^2}}{x }\)
Therefore;
\(tan\left(sin^{-1}\left(\dfrac{3}{4} \right) - cos^{-1}\left(\dfrac{1}{5}\right) \right) = \dfrac{tan\left(sin^{-1}\left(\dfrac{3}{4} \right)\right)-tan\left(cos^{-1}\left(\dfrac{1}{5} \right)\right)}{1-tan\left(sin^{-1}\left(\dfrac{3}{4} \right)\right)\times tan\left(cos^{-1}\left(\dfrac{1}{5} \right)\right)}\)
Which gives;
\(\dfrac{\dfrac{\frac{3}{4} }{\sqrt{1-\left(\frac{3}{4} \right)^2} } -\dfrac{\sqrt{1-\left(\frac{1}{5} \right)^2}}{\frac{1}{5} } }{1+\dfrac{\frac{3}{4} }{\sqrt{1-\left(\frac{3}{4} \right)^2} } \times \dfrac{\sqrt{1-\left(\frac{1}{5} \right)^2}}{\frac{1}{5} }}=\dfrac{\dfrac{3\cdot \sqrt{7}-14\cdot \sqrt{6} }{7} }{\dfrac{7+6\cdot \sqrt{42} }{7} }\)
\(\dfrac{\dfrac{3\cdot \sqrt{7}-14\cdot \sqrt{6} }{7} }{\dfrac{7+6\cdot \sqrt{42} }{7} }=\dfrac{32\cdot \sqrt{6}- 75\cdot \sqrt{7} }{209}\)
Which indicates that we have;
\(tan\left(sin^{-1}\left(\dfrac{3}{4} \right) - cos^{-1}\left(\dfrac{1}{5}\right) \right) =\dfrac{32\cdot \sqrt{6}- 75\cdot \sqrt{7} }{209}\)
Learn more about trigonometric identity here:
https://brainly.com/question/24496175
#SPJ1
PLEASE HELP MEE‼️‼️
Tell me which each 3 boxes should I pick for each one of them PLEASE READ them I beg (proportional relationships)

Answers
number one take the second
An initial amount of 10,000 bacteria is decreasing continuously at a rate of 2% per day. How many bacteria will there be after 2 weeks?
Answers
there will be approximately 7,389 bacteria after 2 weeks of continuous decrease at a rate of 2% per day.
what is exponential?The formula for an exponential function is f (x) = axe, where x is a variable and an is a constant that serves as the function's base and must be bigger than 0. The transcendental number e, or roughly 2.71828, is the most often used exponential function basis.
from the question:
Bacteria are being eliminated at a daily rate of 2%. This means that every day, the quantity of germs reduces by 2% of the previous day's level.
Using the exponential decay method, we can determine how many germs are present after two weeks (14 days):
\(N = N0 * e^(-rt)\)
where N is the number of bacteria after time t, t is the amount of time that has passed in days, r is the rate of reduction (in decimal form), and N0 is the starting number of bacteria.
replacing the specified values:
N0 = 10,000 (initial number of bacteria)
r = 0.02 (rate of decrease is 2% per day)
t = 14 (time elapsed in days)
N = 10,000 *\(e^(-0.02 * 14)\)
Simplifying, we get:
N = 10,000 *\(e^(-0.28)\)
Using a calculator, we get:
N ≈ 7,389
As a result, there will be roughly 7,389 bacteria left after two weeks of steadily declining at a rate of 2% every day.
To know more about exponential:
brainly.com/question/28596571
#SPJ1
What is an equation of the line that passes through the point ) (8,−5) and is parallel to the line
5x+4y=24?
Answers
By rearranging the equation, we get the equation of the line parallel to 5x + 4y = 24 that passes through the point (8, -5) as y = (-5/4)x + 5.To find the equation of a line parallel to another line, we need to determine the slope of the given line.
The equation of a line can be written in slope-intercept form as y = mx + b, where m represents the slope.
To determine the slope of the given line 5x + 4y = 24, we need to rearrange the equation in slope-intercept form. First, subtract 5x from both sides: 4y = -5x + 24. Next, divide all terms by 4: y = (-5/4)x + 6. Therefore, the slope of the given line is -5/4.
Since the line we are looking for is parallel to this line, it will also have a slope of -5/4. Now we can use the point-slope form of a line to find the equation. The point-slope form is given as y - y1 = m(x - x1), where (x1, y1) represents the given point (8, -5) and m is the slope.
Substituting the values into the equation, we have y - (-5) = (-5/4)(x - 8). Simplifying further, y + 5 = (-5/4)x + 10.
For more such questions on equation.
https://brainly.com/question/16949303
#SPJ11
A study was commissioned to find the mean weight of the residents in certain town.
The study found the mean weight to be 187 pounds with a margin of error of 3
pounds. Which of the following is not a reasonable value for the true mean weight of
the residents of the town?
Answers
The value that is not reasonable for the true mean weight of the residents of the town is 193 pounds
Given that the mean weight is 187 pounds with a margin of error of 3 pounds, we can construct the interval as follows:
Mean weight - Margin of error = 187 - 3 = 184 pounds
Mean weight + Margin of error = 187 + 3 = 190 pounds
So, the reasonable range for the true mean weight of the residents of the town is between 184 and 190 pounds.
Now, let's evaluate the options to identify the value that falls outside this reasonable range:
A. 170 pounds - This value falls below the lower limit of the reasonable range (184 pounds). Therefore, it is not a reasonable value for the true mean weight.
B. 188 pounds - This value falls within the reasonable range of 184 to 190 pounds. It is a reasonable value.
C. 193 pounds - This value falls above the upper limit of the reasonable range (190 pounds). Therefore, it is not a reasonable value for the true mean weight.
D. 186 pounds - This value falls within the reasonable range of 184 to 190 pounds. It is a reasonable value.
E. 182 pounds - This value falls below the lower limit of the reasonable range (184 pounds). Therefore, it is not a reasonable value for the true mean weight.
From the options provided, the value that is not reasonable for the true mean weight of the residents of the town is 193 pounds.
Learn more about Margin of Error here:
https://brainly.com/question/16981466
#SPJ1
An initial sample of 458 grams of a radioactive substance decays according to the function A(t)=458e^-0.038t. What is the half-life of the substance?
Answers
If initial sample of 458 grams of a radioactive substance decays according to the function \(A(t)=458e^{-0.038t}\) then the half-life of the substance is 0.
What is half life?Half-life is the time required for a quantity (of substance) to reduce to half of its initial value.
Given,
An initial sample of 458 grams of a radioactive substance decays according to the function
\(A(t)=458e^{-0.038t}\)
We need to find the half life
\(458=458e^{-0.038t}\)
Divide both sides by 458
\(1=e^{-0.038t}\)
Take log on both sides
\(log1=-0.038t\)
0=-0.038t
t=0
Hence, the half-life of the substance is 0.
To learn more on Half life click:
https://brainly.com/question/24710827
#SPJ1
Please break down how to do these pls

Answers
The value of given expressions is -4\(x^{-2}\) + 3\(y^{0}\) = 19 and 2\(x^{0}\)\(y^{-2}\) = 0.08
Simplifying an equation is simply another way of saying solving a math problem. When you simplify a phrase, you are attempting to write it in the simplest way feasible. In conclusion, there should be no more adding, subtracting, multiplying, or dividing to do.
Given expression 1. -4\(x^{-2}\) + 3\(y^{0}\) 2. 2\(x^{0}\)\(y^{-2}\)
Expression for x =2 and y=5
-4x-2 + 3y0
= -4(2)-2 + 3(5)0
= 16+3
=19
Now
2x0y-2
= 2(2)0x(5)-2
= 2 x (1/25)
= 2 x 0.04
= 0.08
Therefore the value of given expressions is -4\(x^{-2}\) + 3\(y^{0}\) = 19 and 2\(x^{0}\)\(y^{-2}\) = 0.08
To learn more about simplification visit
https://brainly.com/question/4356706
#SPJ1
Benjamin had 12 lb of modeling clay. He used 1/5 lb on Monday and another 1/4 lb on Tuesday.
How many pounds of clay does Benjamin have left after Tuesday?
Enter your answer in simplest fractional form in the box.
Answers
Answer:1/2 = 10/20. 1/5 = 4/20. 1/4 = 5/20.
10/20 - 4/20 = 6/20.
6/20 - 5/20 = 1/20 lbs
Step-by-step explanation:
A business gained 50 new customers in April, 100 new customers in May, and 150 new customers in June. During that time, they were running a campaign with a budget of $3000. What was their Customer Acquisition cost?
Answers
Their Customer Acquisition cost was $10
What is customer acquisition cost?Customer Acquisition Cost is the cost of winning a customer to purchase a product or service. As an important unit economic, customer acquisition costs are often related to customer lifetime value. Customer acquisition cost can also be referred as the fee associated with convincing a customer to buy your product or service.
To calculate customer acquisition cost
Customer Acquisition Cost (CAC) = Customer Acquisition Cost/total marketing cost
From the question,
The business gained 50+100+150= 300 new customers
Campaign budget = $30000
Customer Acquisition Cost (CAC) = $3000/300
=$10
Hence, it cost the business $10 to acquire a new customer
Learn more about customer acquisition cost at: https://brainly.com/question/15325223
#SPJ1
What are the solutions to the system of equations? {y=2x2−8x+5y=x−2 (3.5, 0.5) and (1, −1) (7, 5) and (0.5, −1.5) (3.5, 1.5) and (1, −1) (3.5, 1.5) and (−1, −3)
Answers
Answer:
\((1,-1)\) and \((3.5,1.5)\)
Step-by-step explanation:
Given
\(y = 2x^2 - 8x+5\)
\(y = x - 2\)
Required
Determine the solution
Substitute x - 2 for y in \(y = 2x^2 - 8x+5\)
\(x - 2 = 2x^2 - 8x+5\)
Collect like terms
\(0 = 2x^2 - 8x - x + 5 + 2\)
\(0 = 2x^2 - 9x + 7\)
Expand the expression
\(0 = 2x^2 - 7x - 2x+ 7\)
Factorize
\(0 = x(2x - 7) -1(2x - 7)\)
\(0 = (x-1)(2x - 7)\)
Split the expression
\(x - 1 = 0\) or \(2x - 7 = 0\)
Solve for x in both cases
\(x = 1\) or \(2x = 7\)
\(x = 1\) or \(2x/2 = 7/2\)
\(x = 1\) or \(x = 3.5\)
Recall that
\(y = x - 2\)
When \(x = 1\)
\(y = 1 -2\)
\(y = -1\)
When \(x = 3.5\)
\(y = 3.5 - 2\)
\(y = 1.5\)
Hence, the solution is;
\((1,-1)\) and \((3.5,1.5)\)
A graduate student is studying bacteria known to have a growth rate of 7% per day. If the population of a bacterial sample is currently 63,740 bacteria, then how many bacteria will there be in 12 days?
Answers
The number of bacteria in 12 days is 143,555
What is an exponential function?A mathematical function called an exponential function is employed frequently in everyday life. It is mostly used to compute investments, model populations, determine exponential decay or exponential growth, and so on.
Exponential function is a type of function of the form: f(x) = a(b)^x. It is made up of 3 main parts
a = the starting or initial value
b = the base function
x = the exponents
Considering the given problem,
the starting = 63,740 bacteria
the base = 1 + rate = 1 + 0.07 = 1.07
the exponents = x = number of days
The number of bacteria will there be in 12 days
f(x) = a(b)^x
f(x) = 63740 * (1.07)^12
f(x) = 143,555
Learn more about exponential function here:
https://brainly.com/question/29716012
#SPJ1
19.
Your gross income is $4,520.00/month. Your deductions are FICA (7.65%), federal tax withholding (11.75%), and state tax withholding (8.5%). Your fixed expenses are 30% of your realized income. You saved 5 months' worth in an emergency fund, placing 75% in a 60-day CD at a 5.25% APR and the rest in a regular savings account at a 3.8% APR. How much is in the savings account?
$1,969.55
$1,222.10
$1,777.10
$1,315.07
Answers
The correct answer is C. $ 3,666.30 is in the savings account.
What is percentage?A percentage is a number or ratio that can be expressed as a fraction of 100. A percentage is a number or ratio expressed as a fraction of 100. It is often denoted using the percent sign, "%", although the abbreviations "pct.", "pct" and sometimes "pc" are also used. A percentage is a dimensionless number; it has no unit of measurement.
here, we have,
Let's calculate how much money you have in the CD after 5 months, this way:
Gross Income = $ 4,520
Total deductions on taxes = 27.9% (11.75 + 7.65 + 8.50) * 4,520 = $ 1,261.08
Realized income = Gross income - Total deductions on taxes
Realized income = 4,520 - 1,261.08
Realized income = $ 3,258.92
Fixed expenses = 3,258.92 * 0.3 = $ 977.68
Emergency fund = 977.68 * 5 = $ 4,888.40
Certificate of Deposit = 4,888.40 * 0.75 = $ 3,666.30
The correct answer is C. $ 3,666.30
To learn more on percentage click:
brainly.com/question/13450942
#SPJ9
Which are correct representations of the inequality –3(2x – 5) < 5(2 – x)? Select two options.
Answers
The correct representations of the inequality are -6x + 15 < 10 - 5x and x <-5. Options C and D
What are inequalities?Inequalities are described as mathematical relations that makes a non-equal comparison between two elements, variables, numbers or mathematical expressions.
They are often used to compare two numbers on the number line based their sizes.
From the information given, we have the inequality;
–3(2x – 5) < 5(2 – x)
expand the bracket
-6x + 15 < 10 - 5x
collect like terms
-6x + 5x < 10 - 15
add or subtract the like terms
-x < -5
Make 'x' the subject of formula
x < 5
Hence, the value is -6x + 15 < 10 - 5x
Learn more about inequality here:
https://brainly.com/question/25275758
#SPJ1
The complete question:
Which are correct representations of the inequality –3(2x – 5) < 5(2 – x)? Select two options. x < 5 –6x – 5 < 10 – x –6x + 15 < 10 – 5x A number line from negative 3 to 3 in increments of 1. An open circle is at 5 and a bold line starts at 5 and is pointing to the right. A number line from negative 3 to 3 in increments of 1. An open circle is at negative 5 and a bold line starts at negative 5 and is pointing to the left.
I need help with this question please.

Answers
Answer:
It's B. 2/5
Step-by-step explanation:
Because: line G to E is 2/5 of G to F.
Find the sine of angle Ø in the triangle below.

Answers
SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Show the given right-angled triangle
STEP 2: Write the given values for the sides and the appropriate trigonemtric ratio to use
\(\begin{gathered} \text{opposite}=\text{?,adjacent}=9,\text{hypotenuse}=15 \\ \sin \theta=\frac{\text{opposite}}{\text{hypotenuse}} \\ \cos \theta=\frac{\text{adjacent}}{\text{hypotenuse}} \\ \tan \theta=\frac{\text{opposite}}{\text{adjacent}} \end{gathered}\)STEP 3: Get the third side
Since we were to find the sine of the given angle, we need to find the opposite to allow us use the trig ratio in step 2
\(\begin{gathered} U\sin g\text{ pythagoras theorem,} \\ \text{hypotenuse}^2=opposite^2+adjacent^2 \\ \text{hypotenuse}^2-adjacent^2=opposite^2 \\ By\text{ substitution,} \\ 15^2-9^2=opposite^2 \\ \text{opposite}^2=225-81=144 \\ \text{opposite}=\sqrt[]{144}=12 \end{gathered}\)STEP 4: Express the sine of the given angle
\(\begin{gathered} \text{From step 2,} \\ \sin \theta=\frac{opposite}{hypotenuse} \\ \text{opposite}=12,\text{hypotenuse}=15 \\ By\text{ substitution,} \\ \sin \theta=\frac{12}{15} \end{gathered}\)Hence, the sine of the angle is 12/15

need help asap look in file attached

Answers
Answer:
length: 21 cm
width: 16 cm
Step-by-step explanation:
. A rectangle has two lengths and two widths, or two sides that are vertical (up and down) and two sides that are horizontal (left and right)
. In order to find the perimeter we must add up all four side lengths.
. You can find the perimeter of a rectangle by adding the length and the width then multiplying by 2, because there are two of each side length.
P = 2(l+w)
In the question the perimeter is given, which is 74.
We can divide 74 by 2 so that we can find the sum of the length and width.
74/2 = 37
l + w = 37
In the question is states that the length is 5 inches longer than the width.
l = (5 + w)
There are two widths and two lengths in a rectangle, the measurement of the two lengths is 5 inches longer than the two widths.
5 + w + w = 37
5 + 2w = 37
Now that we have our equation we can solve for w, or the width.
1. Move the term containing the variable to the left
5 + 2w = 37
2w + 5 = 37
2. Subtract 5 from both sides of the equation, the opposite of adding 5
2w + 5 = 37
2w + 5 - 5 = 37 - 5
2w = 32
3. Divide by 2 in both sides of the equation, the opposite of multiplying 2
2w = 32
2w/2 = 32/2
4. Cancel out the 2s on the left, but leave the x
2w/2 = 32/2
w = 16
So, now that w, or the width = 16, we can find the length:
l = 5 + w
l = 5 + 16
l = 21
You can check your answer by plugging in our values into the original perimeter formula:
P = 2(l+w)
P = 2(21 + 16)
P = 2(37)
P = 74, so my answer is correct, because 74 is the perimeter given in the question.
The triangle shown has an area of 32.5 square centimeters. Find the measure of the base (segment XY).
Answers
Answer:
XY = 13 cm
Step-by-step explanation:
Area of a triangle formula:
area = base × height / 2
a = bh / 2
Plug numbers into equation:
32.5 = b × 5 / 2
Multiply both sides by 2 to isolate the variable
65 = b × 5
Divide both sides by 5 to isolate the variable
13 = b
Check your work:
32.5 = 13 × 5 / 2
32.5 = 65 / 2
32.5 = 32.5
Correct
Nelson lands 4650 on 2% interest rate. He plans to pay this after 2 months. What will the total principal and interest payment be?
Answers
The total principal and interest payment that Nelson will have to pay after 2 months is $4665.50.
To calculate the total principal and interest payment, we need to determine the interest amount and add it to the principal.
First, let's find the interest amount:
Interest = Principal x Interest Rate x Time
Given:
Principal = $4650
Interest Rate = 2% per year
Time = 2 months
Since the interest rate is given on an annual basis, we need to convert the time from months to years. There are 12 months in a year, so 2 months is equivalent to 2/12 = 1/6 years.
Interest = $4650 x 0.02 x (1/6) = $15.50
Now, we can calculate the total principal and interest payment:
Total Payment = Principal + Interest
Total Payment = $4650 + $15.50 = $4665.50
For more such questions on principal visit:
https://brainly.com/question/25720319
#SPJ8
What are 2 institutions from the Industrial Revolution? NEED ANSWER NOW PLEASE!!!!!!!
A. Corporations
B. National Institute of Space and Technology
C. Labor Unions
D. National Institute of Disaster Management
Answers
The institution from the industrial revolution is the national institute of space and technology. Hence, option B is correct.
What is Industrial Revolution?Agrarian and handcraft economies were replaced by industrialized and machine production during the Industrial Revolution in modern history. New modes of living and working were made possible by these technical advancements, which profoundly altered society.
In the 18th century, this practice started in Britain and then extended to other regions of the world. The English economics professor Arnold Toynbee (1852–83), who originally used the word to characterize Britain's economic growth from 1760 to 1840, although it had been used by French writers earlier.
To know more about Industrial Revolution:
https://brainly.com/question/855594
#SPJ1
Select the correct answer from each drop-down menu.
The total area of the three triangles is
square units.
The area of the figure is
square units.
Answers
The total area of the three triangles is square units is 36 and the area of the figure is square units is 60.
What is the triangle?The triangle can be defined as a three-sided polygon in geometry, and it consists of three vertices and three edges. The sum of all the angles inside the triangle is 180°.
From the figure, the area of triangles can be calculated using the:
Area = (1/2)height×base length
Area of three triangle = 1/2(4×6) + 1/2(6×4) + 1/2(4×6)
Area of three triangle = 1/2(24×3) = 36 square units
Area of the figure = area of three triangle + area of the rectangle
= 36 + 6×4
= 60 square units
Thus, the total area of the three triangles is square units is 36 and the area of the figure is square units is 60.
Learn more about the triangle here:
brainly.com/question/25813512
#SPJ1

Ullany TVd How much 20k stamps can #2.00 buy
Answers
Answer: 4000
Step-by-step explanation:
(5k+35) -8=12 need help solving this
Answers
Answer:
k= -6.48 approx
Step-by-step explanation:
(5k+35) -8=12
opening bracket
-45k-280=12
-45k=12+280
-45k=292
k=-6.48 approx
Answer:
Step-by-step explanation:
I don't say you have to mark my ans as brainliest but if you think it has really helped you plz don't forget to thank me...

Alex records the running time—the number of minutes a movie lasts from start to finish—of 50 popular movies. The distribution of times, in minutes, is displayed in the histogram below.
A histogram titled Movie running times has time (minutes) on the x-axis and frequency on the y-axis. 80 to 90, 8; 90 to 100, 15; 100 to 110, 13; 110 to 120, 6; 120 to 130, 4; 130 to 140, 2; 140 to 150, 1; 150 to 160, 1.
Which of the following correctly describes the shape of the distribution?
A. uniform
B. skewed left
C. skewed right
D. roughly symmetric

Answers
The shape of the distribution is skewed right.
Option C is the correct answer.
What is a histogram?A histogram is an representation of the distribution of data with intervals.
We have,
From the histogram, we see that,
The shape of the distribution is skewed right.
For skewed distributions,
We have one tail of the distribution considerably longer relative to the other tail.
A skewed right distribution is one in which the tail is on the right side.
We get,
Mode > Mean > Median.
A skewed left distribution is one in which the tail is on the left side.
A figure is given below to compare the distribution.
Thus,
The shape of the distribution is skewed right.
Learn more about histograms here:
https://brainly.com/question/16819077
#SPJ1
Write the given second order equation as its equivalent system of first order equations. u′′−5u′−4u=1.5sin(3t),u(1)=1,u′(1)=2.5 Use v to represent the "velocity function", i.e. v=u′(t). Use v and u for the two functions, rather than u(t) and v(t). (The latter confuses webwork. Functions like sin(t) are ok.)
Answers
Answer:
hi your question options is not available but attached to the answer is a complete question with the question options that you seek answer to
Answer: v = 5v + 4u + 1.5sin(3t),
0 1 4 5 0 1.5sin(3t) 1 2.5Step-by-step explanation:
u" - 5u' - 4u = 1.5sin(3t) where u'(1) = 2.5 u(1) = 1
v represents the "velocity function" i.e v = u'(t)
As v = u'(t)
u' = v
since u' = v
v' = u"
v' = 5u' + 4u + 1.5sin(3t) ( given that u" - 5u' - 4u = 1.5sin(3t) )
= 5v + 4u + 1.5sin(3t) ( noting that v = u' )
so v' = 5v + 4u + 1.5sin(3t)
d/dt \(\left[\begin{array}{ccc}u&\\v&\\\end{array}\right]\)= \(\left[\begin{array}{ccc}0&1&\\4&5&\\\end{array}\right]\) \(\left[\begin{array}{ccc}u&\\v&\\\end{array}\right]\) + \(\left[\begin{array}{ccc}0&\\1.5sin(3t)&\\\end{array}\right]\)
Given that u(1) = 1 and u'(1) = 2.5
since v = u'
v(1) = 2.5
note: the initial value for the vector valued function is given as
\(\left[\begin{array}{ccc}u(1)&\\v(1)\\\end{array}\right]\) = \(\left[\begin{array}{ccc}1\\2.5\\\end{array}\right]\)

Triangle ABC has coordinates A(4, 1), B(5, 9), and C(2, 7). If the triangle is translated 7 units to the left, what are the coordinates of B'?
Answers
Answer:
(-2,9)
Step-by-step explanation:
7 to the left would only change the x coordinate
Use the substitution u = 9x2 + 8 to find the following indefinite integral Check your answer by differentiation '18x sin (9x2 + 8) 18x sin (9x2 + 8) dx=
Answers
The value of the given indefinite integral is found to be: y = -cos (9x² + 8) + c.
Explain about the indefinite integral?A function that accepts the antiderivative of that other function is said to take an endless integral. Visually, it is shown as an integral indicator, a function, and finally a dx. It is simpler to represent taking the antiderivative using the indefinite integral.The given integral is;
y = ∫18x sin (9x² + 8) dx
Put u = 9x² + 8
Then, on differentiation
18x dx = du
substitute the values:
y = ∫ sin (u) du.
y = -cos u
Put u = 9x² + 8
y = -cos (9x² + 8) + c
c is the constant of integration.
Thus, the value of the given indefinite integral is found to be: y = -cos (9x² + 8) + c.
To know more about the indefinite integral, here
https://brainly.com/question/27419605
#SPJ4
which fraction is equivalent to 6/12
Answers
Answer:
1/2
Step-by-step explanation:
....................
Same set up as the problem to the left. Fill in the blanks.

Answers
The blanks that are missing in the sequence are -3 and 11
How to fil in the blanks in the sequencefrom the question, we have the following parameters that can be used in our computation:
The blanks in the sequence
When listed out, we have
_, _, 25, 39
Assuming that the sequence, is an arithmetic sequence, then we have
Common difference = 39 - 25
Common difference = 14
This means that
Previous term = 25 - 14 = 11
Firs term = 11 - 14 = -3
So, the missing terms are -3 and 11
Read more about sequence at
https://brainly.com/question/30499691
#SPJ1
