Calculate the APR for a $2000 loan that is paid off in 12 equal monthly payments. The stated annual interest rate is 8%. Show your work.
Answers
The APR (annual percentage rate) for a $2,000 loan paid off in 12 equal monthly payments with a stated annual interest rate of 8% is 14.452%.
How the APR is computed:The annual percentage rate (APR) can be determined using an online finance calculator as follows:
The APR is the total cost of borrowing money, reflecting not only the interest rate but also other loan fees.
N (# of periods) = 12 months
PV (Present Value) = $2,000
PMT (Periodic Payment) = $-180
FV (Future Value) = $-0
Results:
I/Y = 14.452% if interest compounds 12 times per year (APR)
I/Y = 15.449% if interest compounds once per year (APY)
I/period = 1.204% interest per period
Sum of all periodic payments = $-2,160.00 ($180 x 12)
Total Interest = $160.00 ($2,000 x 8%)
Learn more about the annual percentage rate (APR) at https://brainly.com/question/2772156.
#SPJ1
Related Questions
Tina currently has $60 and is earning $4 a day dog walking. Tony has $68 and is spending 3$ a day on candy! In how many days will they both have the same amount of candy?
Answers
Answer:
8 days
Step-by-step explanation:
Let us represent the number of days as x
For Tina
Tina currently has $60 and is earning $4 a day dog walking.
= $60 + $4 × x
= 60 + 4x
For Tony
Tony has $68 and is spending 3$ a day on candy!
= $68 + $3 × x
= 68 + 3x
To calculate the number of days that they will both have the same amount of candy we equate both equations to each other
60 + 4x = 68 + 3x
Collect like terms
4x - 3x = 68 - 60
x = 8 days
Therefore, they will both have the same amount of candy in 8 days
An internet service provider charges a $35 sign-up fee and $40 per month for an internet plan. Which representation shows the relationship between the number of months, x, and the total cost of the internet plan, y? What is it?
Answers
Answer:
Y= 35+40x
Step-by-step explanation:
You pay $40 a month. The total is Y. And the Beginning Fee is $35! Please mark me brainliest, and have a great day!
Answer:Y= 35+40x
Step-by-step explanation:
Let f(x) = x3 + 3x2 -9x + 14
a. On what interval is f increasing (include the endpoints in the interval)?
b. On what interval is f concave downward (include the endpoints in the interval)?
Answers
The function f(x) is concave downward on the interval (-∞, -1).
a. To determine the interval on which the function f(x) = x³+ 3x² - 9x + 14 is increasing, we need to find the values of x for which the derivative of f(x), denoted as f'(x), is positive.
Taking the derivative of f(x) with respect to x, we get:
f'(x) = 3x² + 6x - 9.
Setting f'(x) > 0, we have:
3x² + 6x - 9 > 0.
Factoring the left-hand side of the inequality, we get:
3(x² + 2x - 3) > 0.
Now, solving for x, we have:
x²+ 2x - 3 > 0.
To find the values of x that satisfy this inequality, we can factor the quadratic expression on the left-hand side:
(x + 3)(x - 1) > 0.
From this expression, we can see that the inequality is satisfied when x < -3 or x > 1. Therefore, the function f(x) is increasing on the intervals (-∞, -3) and (1, ∞), and including the endpoints, the interval on which f(x) is increasing is [-∞, -3] U [1, ∞].
b. To determine the interval on which the function f(x) is concave downward, we need to find the values of x for which the second derivative of f(x), denoted as f''(x), is negative.
Taking the second derivative of f(x) with respect to x, we get:
f''(x) = 6x + 6.
Setting f''(x) < 0, we have:
6x + 6 < 0.
Solving for x, we get:
x < -1.
Therefore, the function f(x) is concave downward on the interval (-∞, -1), including the endpoint, the interval on which f(x) is concave downward is [-∞, -1].
To know more about Concave downward refer here:
https://brainly.com/question/29121586
#SPJ11
A coffee shop is running a promotion where a number of free coffee samples are given away each day. The equation above can be used to model the number of free coffee samples, y, that remain to be given away x days after the promotion began. What does it mean that (11, 0) is a solution to this equation?
110xy = 1,210
A) During the promotion, 11 samples are given away each day.
B) It takes 11 days during the promotion to see 1,210 customers.
C) It takes 11 days during the promotion until none of the samples are remaining.
D) There are 11 samples available at the start of the promotion
Answers
Answer:
C
Step-by-step explanation:
First, let us clarify what (11, 0) represent
(x, y) ---> (11, 0)
The values are as followed:
x = 11
y = 0
If the problem states that x is the number of days after the promotion started, then it will be 11 days.
When we assert that it has been 11 days, we rule answers A and D.
If the problem states that y is the number of free coffee samples that remain after 11 days (because x is included in this statement), then it will be 0 samples.
Therefore, the answer will be C. After 11 days of the promotion, there will be 0 samples that are left.
there are 5 black balls and 9 red balls in an urn. if 5 balls are drawn without replacement, what is the probability that exactly 3 black balls are drawn? express your answer as a fraction or a decimal number rounded to four decimal places.
Answers
The probability of drawing exactly 3 black balls out of 5 is 0.2846, or approximately 0.2846 rounded to four decimal places.
To find the probability of drawing exactly 3 black balls out of 5, we need to use the binomial probability formula, which is:
P(X=k) = (n choose k) * p * (1-p)ⁿ⁻ᵏ
where P(X=k) is the probability of getting k successes, n is the number of trials, p is the probability of success, and (n choose k) is the number of ways to choose k items out of n.
In this case, n = 5, k = 3, p = 5/14 (the probability of drawing a black ball on the first draw is 5/14, and this probability decreases with each subsequent draw), and (n choose k) = 5 choose 3 = 10 (the number of ways to choose 3 black balls out of 5).
Plugging these values into the formula, we get:
P(X=3) = (5 choose 3) * (5/14)³ * (9/14)²
= 10 * 0.0752 * 0.3778
= 0.2846
To learn more about probability click on,
https://brainly.com/question/29196823
#SPJ4
\(3x-4=14\\\)
Answers
\(\text {Hello! Let's Solve this Problem!}\)
\(\text {\underline {The First Step is to Add 4}}\)
\(\text {3x-4+4=14+4}\)
\(\text {3x=18}\)
\(\text {\underline {The Final Step is to Divide 3}}\)
\(\text {3x/3=18/3}\)
\(\text {Your Answer Would Be:}\)
\(\Huge\boxed {x=6}\)
\(\text {Best of Luck!}\)
\(\huge\text{$x=\boxed{6}$}\)
We can solve for the variable \(x\) by isolating it on one side of the equals sign.
Start by adding \(4\) to both sides to cancel out the \(-4\) on the left side of the equation.
\(\begin{aligned}3x-4+4&=14+4\\3x&=18\end{aligned}\)
Now divide both sides of the equation by \(3\) since \(3x\) is the same as \(3*x\) and we want to isolate \(x\), keeping in mind that anything multiplied by \(1\) is itself.
\(\begin{aligned}3x&=18\\3*x&=18\\3*x\div3&=18\div3\\x*3\div3&=18\div3\\x*1&=6\\x&=\boxed{6}\end{aligned}\)
A linear function contains the following points. X - 4 | 4 0 5 What are the slope and y-intercept of this function?
A. The slope is 4. The y-intercept is (5.
B. The slope is The y-intercept is (0,5).
C. The slope is - 1 Tthe y-intercept is (0,5).
D. The slope is -4. The y-intercept is (0,5).
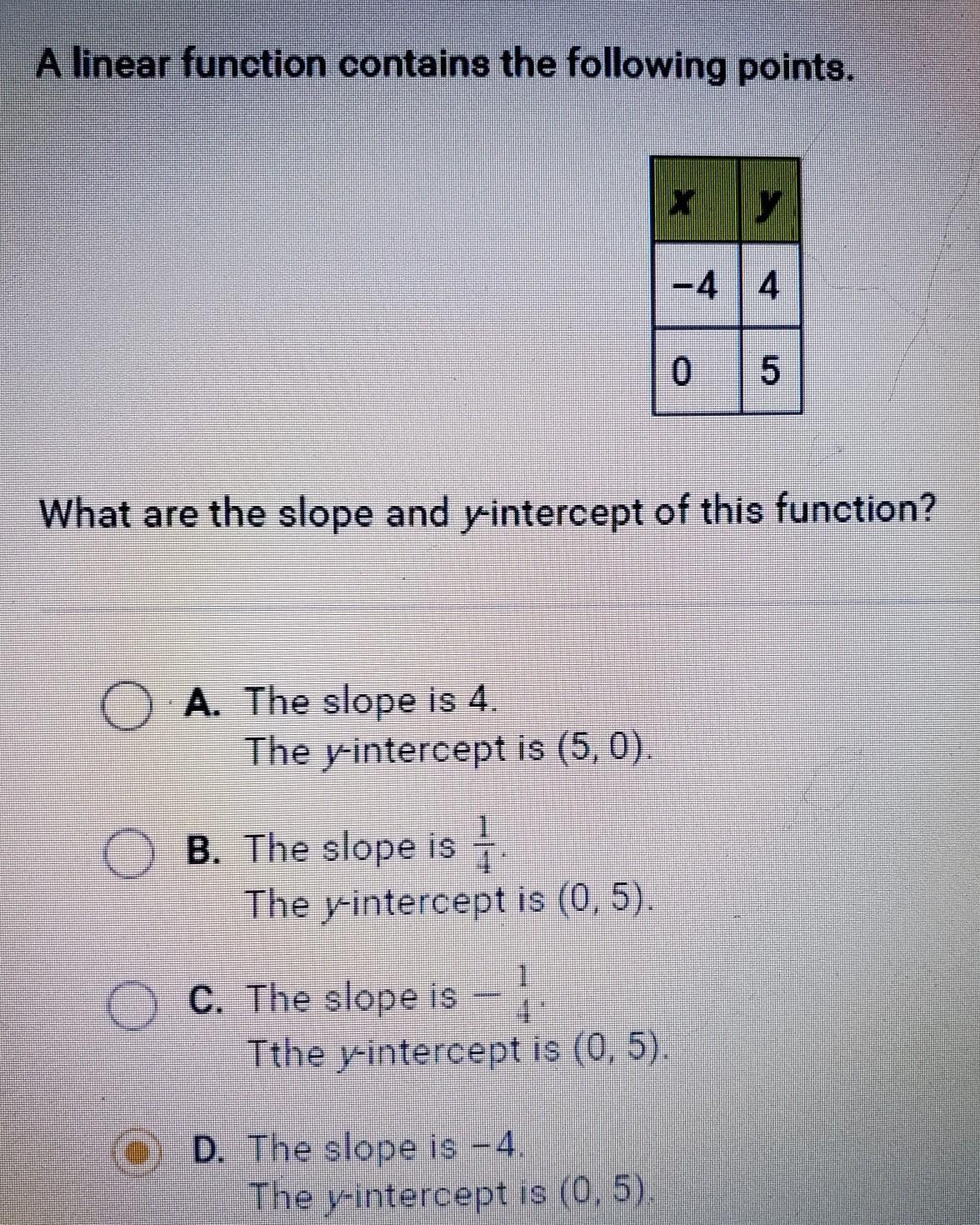
Answers
Answer:
The answer is B.
Step-by-step explanation:
when x is 0, y is 5. So that is the yintercept and 4-5=-1 -4-0=-4 do 1/4
Lin can type 192 words in 6 minutes. Hoi can type 112 words in 4 minutes. Which statement is true?
A.Hoi can type 4 more words per minute than Lin.
B.Lin can type 4 more words per minute than Hoi.
C.Lin can type 8 more words per minute than Hoi.
D.Hoi can type 8 more words per minute than Lin.
Answers
Answer:
112 words in 4 minutes
Step-by-step explanation:
Hoi can type 112 words in 4 minutes. Therefore, Lin's typing speed is 32 words per minute. Therefore, Hoi's typing speed is 28 words per minute. We can see that Lin's typing speed is 4 more (32-28) words per minute more than Hoi, therefore, option B is the correct choice.
A function f: t1 -> t2 is total iff for all values x: t1, f x is valuable. We have to evaluate whether it's true or false
Answers
The statement "A function f: t1 -> t2 is total iff for all values x: t1, f x is valuable" is true.
In other words, for every element x in the domain t1, the function f must produce a meaningful output in the codomain t2. To evaluate the truthfulness of this statement, we need to consider the definition of a function and its properties.
A function maps each element from the domain to a unique element in the codomain. Therefore, for a function to be total, it must cover all elements in the domain and assign a valid value in the codomain.
Let's suppose we have a function f: t1 -> t2. To determine if it is total, we need to check if it satisfies the condition for all values x in t1. If there is any element x in t1 for which f does not produce a valid value in t2, then the function is not total.
However, if for every x in t1, f(x) produces a valid value in t2, then the function is considered total.
The evaluation of whether a function is total or not depends on the specific definition of the function and the domain and codomain involved. It is important to ensure that the function is defined for all elements in the domain and that it assigns a meaningful output for each input value.
In summary, a function f: t1 -> t2 is total if it produces a valid value in t2 for every element in the domain t1.
To know more about function refer here:
https://brainly.com/question/31017064#
#SPJ11
A gumball machine contains 7 red, 5 yellow, and 6 orange gumballs. What is the probability that the next gumball that comes out will be either red or yellow?
show work pls tnx!
Answers
Answer:
2/3
Step-by-step explanation:
7 red, 5 yellow, and 6 orange =18
P( red or yellow) = number of red or yellow / total
= (5+7)/18
=12/18
=2/3
Question 3
20 pts
A map uses the scale of 2 inches represents 3 miles. If the actual distance between two
cities is 27 miles, then what is the length on the map?
Answers
The length on the map representing the 27 miles between the two cities is 18 inches.Therefore, the length on the map would be 18 inches.
To solve this problem, we can use the scale of the map to set up a proportion:
2 inches / 3 miles = x inches / 27 miles
We can then cross-multiply to solve for x:
3x = 2 * 27
3x = 54
x = 18
Therefore, the length on the map would be 18 inches.
To find the length on the map representing the actual distance between two cities, we'll use the given scale:
2 inches represents 3 miles.
First, we'll determine the ratio between inches and miles:
2 inches / 3 miles
The actual distance between the cities is 27 miles. To find the corresponding length on the map, we can set up a proportion:
Length on map (in inches) / 27 miles = 2 inches / 3 miles
Next, we'll solve for the length on the map (in inches):
Length on map (in inches) = (2 inches / 3 miles) * 27 miles
The miles cancel out, and we're left with:
Length on map (in inches) = (2 inches * 27) / 3
Length on map (in inches) = 54 inches / 3
Length on map (in inches) = 18 inches
So, the length on the map representing the 27 miles between the two cities is 18 inches.
Visit here to learn more about length : https://brainly.com/question/20985033
#SPJ11
nine people sit down at random seats around a round table. four of them are math majors, three others are physics majors, and the two remaining people are biology majors. what is the probability that all four math majors sit in consecutive seats?
Answers
The probability that all four math majors sit in consecutive seats is;
1/126.
There are a total of;
9! = 362880 possible ways for the people to sit down at the table, since the order in which they sit matters.
Since there are 9 places that the group of 4 math majors can start, the group must be seated consecutively, so there is only 1 way to seat the math majors once a starting point has been chosen.
To find the number of ways that all four math majors can sit in consecutive seats therefore, we should first seat the math majors and then seat the other people.
There are 5! (5 factorial) ways to seat the other people, since the order in which they sit does not matter. Thus, there are a total of;
4! * 5! = 4! * 120 = 480 ways for the math majors to sit in consecutive seats.
If we do not consider math majors first, here are 6! = 720 ways to arrange the math, physics, and biology majors around the table, and for each of these arrangements, there are 4! = 24 ways to arrange the math majors in the 4 seats.
Thus, the probability that all four math majors sit in consecutive seats is 480/9! = 1/126.
To find more on probability, look into:
brainly.com/question/30034780
#SPJ4
can you please help me??

Answers
V= 14 1/2 • 6 1/2 • 5
V = 471. 25 inches
6 is added to the
product of 7 and a number.
Answers
The equation model of the given statement in question is 6 + 7× x.
What are equation models and arithmetic?The model of equation is defined as the model of the given situation in the form of an equation using constants and variables.
In math, it deals with numbers of operations given according to the statements. The four major arithmetic operators are, addition, subtraction, multiplication, and division.
Given that;
6 is added to product of a number and 7
Now,
Let, the number multiplied by 7 be x,
=7*x
6 is added to the product;
= 6 + 7 × x
Therefore, the equation of model will be given as 6 + 7 × x;
To know more about models visit:
brainly.com/question/22591166
#SPJ9
The directions on a seed packet say to plant the seeds 178 inches apart. What is the decimal equivalent of this mixed number?Enter your answer in the box.
Answers
The Decimal equivalent of the mixed number is 1.875
Given:
Mixed number = 1⁷/₈ inches
First step is to convert from mixed number to simple fraction
Simple fraction= [(8 × 1) + 7]/ 8
Simple fraction= (8 + 7) / 8
Simple fraction= 15 / 8
Now let Convert the simple fraction to decimal equivalent:
Decimal equivalent= 15 ÷ 8
Decimal equivalent= 1.875
Therefore the Decimal equivalent of the mixed number is 1.875.
Learn more here:
https://brainly.com/question/6462615
what is the vertex and axis of symmetry for this?

Answers
Answer:
Vertex is (0,0)
Axis of Symmetry is 0
Step-by-step explanation:
A vertex is the highest or lowest point of the parabola where the curve ends. An axis of symmetry is what number (on the x-axis) the vertex is on. There is an invisible up and down dotted line that marks the axis of symmetry.

The weights of certain candles are normally distributed with a mean of 720mg and a standard deviation of 20mg. What proportion of candles weigh between 695mg and 734mg?
Answers
Answer:
ufoufoydiyd8yf86fiyxitdkydyofiyd8yfoyfoycoycoycoycoyfiyfiyfyocyiciycigxitc8txitditxt8xtix8tx8td8yd8yc8yyc8yf58d8txt7x85d85duts7td8txits
Step-by-step explanation:
yfid8yydyofoyf0
Add: 410 + 210 Write your answer in simplest terms
Answers
The addition of two numbers is 410+210 is 620.
From the given numbers,
First number is 410
Second number is 210.
One of the arithmetic operations is addition. The total of the numbers is provided. In other words, addition refers to the operation of adding the numbers together. "+" is the symbol used to denote addition. The outcome of the adding procedure is referred to as the sum. Addends are the numbers that are added together.
One of the four fundamental mathematical operations, addition indicates the sum of two or more numbers added together.The following are the rules of addition operation:
Positive Number + Positive Number = (Add) Positive NumberNegative Number + Negative Number = (Add) Negative NumberNegative Number + Positive Number = (Subtract) Take the sign of the number with the largest absolute valueNow,
⇒410+210=620
Therefore, the value is 620.
For more such questions on simplest form
https://brainly.com/question/14100507
#SPJ4
Eight out of 100 =___%
Answers
...........
Answer:
8%
Step-by-step explanation:
Hope this helps :)
A bicycle is on sale for $189.00. The sales tax rate is 5%. How much is the sales tax?
Answers
Answer:
The tax rate is 9 dollars and 45 cents.
Step-by-step explanation:
Pls help I’m getting confused even though should be pretty easy.

Answers
Answer:
V = 108
Step-by-step explanation:
B = 9 x 4 = 36 Height of Triangular prism is 3 so 36 x 3 = 108
pls answer
brainiest guaranteed
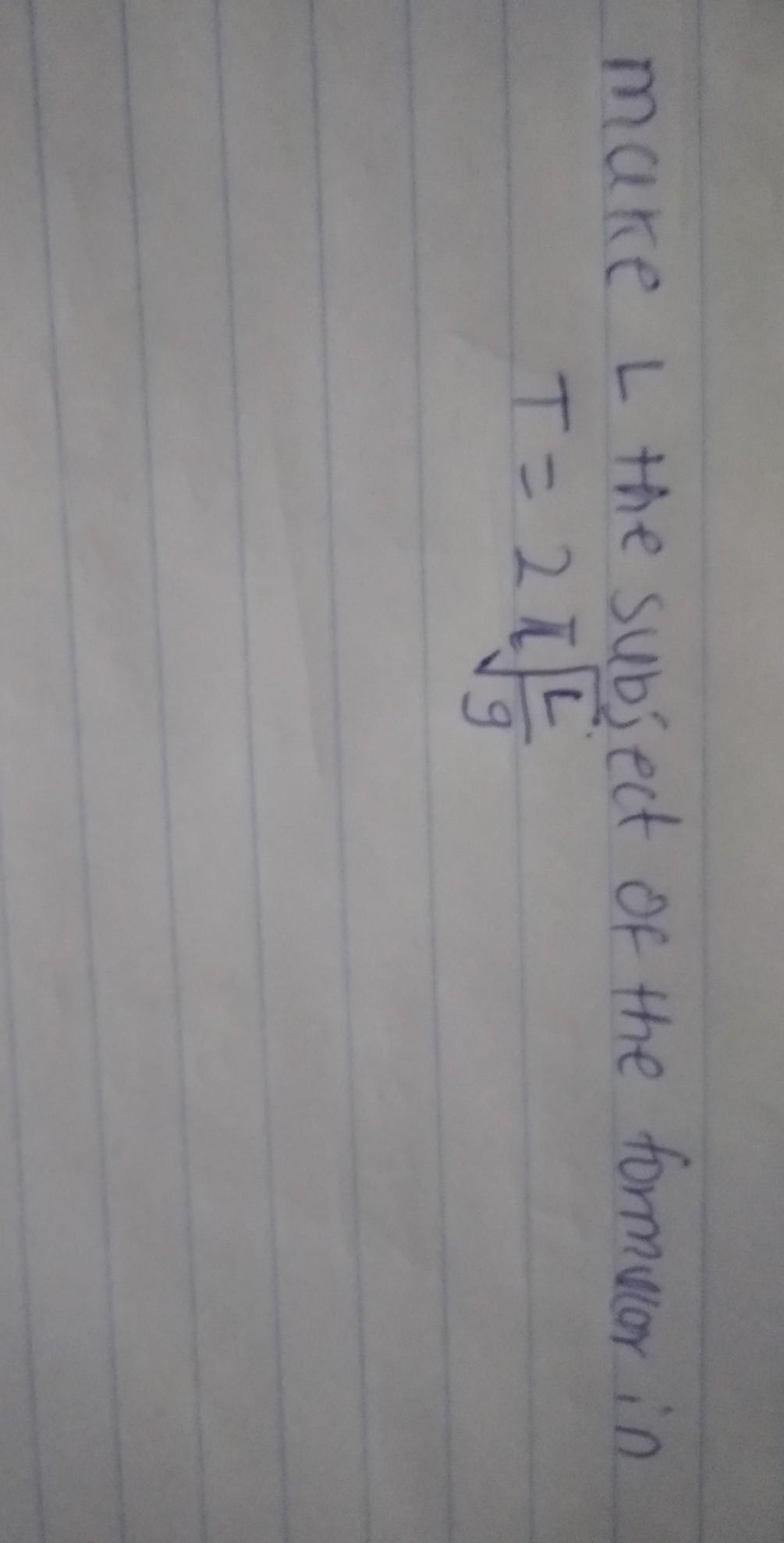
Answers
Answer:
T^2g / (4 pi^2) = L
Step-by-step explanation:
T = 2 pi sqrt( L /g)
Divide each side by 2 pi
T / 2 pi = 2 pi sqrt( L /g) / 2 pi
T / 2 pi = sqrt( L /g)
Square each side
(T / 2 pi) ^2 =( sqrt( L /g))^2
T^2 / (4 pi^2) = L /g
Multiply each side by g
T^2 / (4 pi^2) *g= L /g *g
T^2g / (4 pi^2) = L
Answer:
Step-by-step explanation:

An important application of the chi-square distribution is a. testing for goodness of fit b. testing for the independence of two variables c. both of the above d. none of the above
Answers
An important application of the chi-square distribution is testing for goodness of fit and testing for the independence of two variables The correct answer is c. both of the above.
The chi-square distribution is a probability distribution that is used in statistics for hypothesis testing and confidence interval estimation. Two important applications of the chi-square distribution are testing for goodness of fit and testing for the independence of two variables.
Testing for goodness of fit involves comparing observed data to expected data, and determining whether the differences between the observed and expected data are statistically significant. The chi-square distribution is used to calculate a test statistic, which measures the degree of divergence between the observed and expected data.
Testing for the independence of two variables involves examining whether there is a relationship between two categorical variables. The chi-square distribution is used to calculate a test statistic that measures the degree of dependence or independence between the two variables. If the test statistic is large enough, it indicates that there is a significant relationship between the two variables.
for such more question on chi-square distribution
https://brainly.com/question/17142834
#SPJ11
The foundation of a building is in the shape of a rectangle, with a length of 20 meters (m) and a width of 18 m.
Answers
The distance from the top left corner of the foundation to the bottom right corner is 27 meters.
The distance between two points in space can be calculated using the Pythagorean theorem. In this case, we want to find the distance from the top left corner of the foundation to the bottom right corner.
To do this, we will use the length and width of the foundation, which are 20 meters and 18 meters respectively.
The Pythagorean theorem states that in a right triangle, the square of the distance (c) between the two points is equal to the sum of the squares of the other two sides (a and b). Mathematically, this can be represented as
=> c² = a² + b².
In our case, the two sides are the length (20m) and width (18m) of the foundation. To find the distance, we will first find the square of c by adding the squares of a and b. So,
=> c² = 20² + 18² = 400 + 324 = 724.
To find the distance, we will take the square root of c².
So,
c = √724 = 26.83
When we rounded to the nearest meter, c = 27m.
Complete Question:
The foundation of a building is in the shape of a rectangle, with a length of 20 meters(m) and a width of 18m. To the nearest meter, what is the distance from top left corner of the foundation to the bottom right corner.
To know more about rectangle here.
https://brainly.com/question/8663941
#SPJ4
Find the volume of a right circular cone that has a height of 11.9 ft and a base with a radius of 16.3 ft. Round your answer to the nearest tenth of a cubic foot.
Answers
Answer:
V≈3310.94ft³
Step-by-step explanation:
explanation is in screenshot.

How do I solve for Y?

Answers
Start with the small triangle on the right:
35 + 96 + x = 180
x = 49
Ah, you already have that. Nice!
Now move to the biggest triangle:
x + 77 + (35+y) = 180
but x = 49, so
49 + 77 + 35+y = 180
y = 19
Solve the following linear system of equations by Cramer's rule method;
2x+4y+2z=16
−2x−3y+z=−5
2x+2y−3z=−3
Rearrange as the form of Ax=B
Find the inverse of the coefficient matrix (A⁻¹); and
Solve the system of equations
Answers
The solution of the given linear system of equations is x = 2, y = 1 and z = 2.
Given that the linear system of equations is
2x + 4y + 2z = 16-2x - 3y + z = -52x + 2y - 3z = -3
To solve the system of equations by Cramer's rule method, arrange them in the form of Ax = B as below:
A = [2, 4, 2; -2, -3, 1; 2, 2, -3], x = [x, y, z] and B = [16, -5, -3]
To find the inverse of the coefficient matrix A⁻¹, first, find the determinant of A as below:
|A| = 2[-3 - 2] - 4[-2 + 2] + 2[-8 + 1] = -12
The determinant is non-zero, hence A is invertible
A⁻¹ = 1/|A| [adj A]
where adj A is the transpose of the cofactor matrix [C] of A:
adj A = [C]T
So, we find [C] by replacing each element of A with its cofactor and taking its transpose matrix as below:
C = [5, 2, 6; 2, -2, 2; -4, -4, -4]
Then [C]T = [5, 2, -4; 2, -2, -4; 6, 2, -4]So, A⁻¹ = 1/|A| [adj A] = 1/(-12) [5, 2, -4; 2, -2, -4; 6, 2, -4] = [-5/6, -1/2, 1/2; -1/6, 1/2, 1/2; 1/2, 1/2, 1/2]
To solve the system of equations, we have x = A⁻¹B as below:
x = [-5/6, -1/2, 1/2; -1/6, 1/2, 1/2; 1/2, 1/2, 1/2][16; -5; -3] = [2; 1; 2]
To know more about linear system, visit:
https://brainly.com/question/26544018
#SPJ11
Determine the solution set for x.
X - 180 > 120
Answers
The solution set for x is all values greater than 300. means that any value of x greater than 300 would make the inequality true.
The given inequality is: x - 180 > 120
To solve for x, we need to isolate x on one side of the inequality. We can start by adding 180 to both sides:
x - 180 + 180 > 120 + 180
x > 300
So the solution set for x is all values greater than 300. We can express this in interval notation as (300, infinity) or using set builder notation as {x | x > 300} This means that any value of x greater than 300 would make the inequality true.
To know more about value click here
brainly.com/question/30760879
#SPJ11
true or false: 3^-1 x 3^-1=3^1
Answers
Answer:
the answer I got is false
For the past 16 months, susie has been paying $126.50 each month to her insurance company. after causing an accident last month, her insurance company notified her that her monthly payment will be increased by $21.25. what increase in her annual premium did susie’s insurance company apply as a result of the accident? a. $21.25 b. $125.60 c. $147.75 d. $255.00 please select the best answer from the choices provided a b c d
Answers
The annual premium of Susie's insurance company apply as a result of accident is $255 for an year. This is because the monthly insurance payment has been increased by $21.25.
What is Health insurance?
Health insurance or the medical insurance is an insurance which covers the whole or a part of the risk of a person which is incurring the medical expenses. Depending upon the health insurance plan, the risk is shared among many individuals.
Main body:
The increase in monthly insurance payment = $21.25
So, the annual increase in the premium amount paid by Susie will be:
Monthly increase in insurance payment × 12
(As there are 12 months in an year)
Annual increase in premium amount = $21.25 × 12
Annual increase in premium amount = $255
Therefore, the annual increase in the amount of premium paid by Susie for health insurance is $225.
Learn more about Health insurance here:
brainly.com/question/29042328
#SPJ4