C an someone show me step by step how to do this and correctly please
A city just opened a new playground for children in the community. An image of the land that the playground is on is shown.
A polygon with a horizontal top side labeled 45 yards. The left vertical side is 20 yards. There is a dashed vertical line segment drawn from the right vertex of the top to the bottom right vertex. There is a dashed horizontal line from the bottom left vertex to the dashed vertical, leaving the length from that intersection to the bottom right vertex as 10 yards. There is another dashed horizontal line that comes from the vertex on the right that intersects the vertical dashed line, and it is labeled 12 yards.
What is the area of the playground?
900 square yards
855 square yards
1,710 square yards
1,305 square yards
Answers
First, let's find the area of the rectangle. The rectangle has a height of 20 yards and a width of 10 yards + 12 yards = 22 yards. So the area of the rectangle is:
Area of rectangle = height x width
Area of rectangle = 20 yards x 22 yards
Area of rectangle = 440 square yards
Next, let's find the area of the two triangles. The triangle on the left has a base of 20 yards and a height of 45 yards. So the area of the triangle is:
Area of triangle 1 = (1/2) x base x height
Area of triangle 1 = (1/2) x 20 yards x 45 yards
Area of triangle 1 = 450 square yards
The triangle on the right has a base of 12 yards and a height of 20 yards. So the area of the triangle is:
Area of triangle 2 = (1/2) x base x height
Area of triangle 2 = (1/2) x 12 yards x 20 yards
Area of triangle 2 = 120 square yards
Finally, we can add up the areas of the rectangle and the two triangles to get the total area of the playground:
Total area = area of rectangle + area of triangle 1 + area of triangle 2
Total area = 440 square yards + 450 square yards + 120 square yards
Total area = 1,010 square yards
Therefore, the area of the playground is 1,010 square yards.
HOPE THIS HELPS
Related Questions
The numbered list gives instructions to bisect a line segment, but the steps are out of order.
1. Use a straightedge or ruler to draw a straight line from the point where the arcs cross above the line segment to the point where the arcs cross below
2. Adjust the compass so that it is just a bit larger than half of the length of the line segment.
3. Use the compass to draw arcs above and below the line segment.
4. Place the pointed end of a compass at one of the terminal points of the line segment.
5. Without changing the compass width, place the point at the other terminal point, and draw arcs above and below the lir
If the line segment is already given, which is the correct order of the remaining steps to bisect the line segment?
O 1, 3, 2, 4, 5
O 3, 5, 1, 4, 2
O 4, 2, 3, 5, 1
O 5, 4, 3, 2, 1
Answers
Answer: 4, 2, 3, 5, 1
Step-by-step explanation:
First, you need to set your compass width or set the compass at one of the terminal points.
After, you can draw arcs above and below.
Then, repeat for the other terminal point.
Finally, connect the intersection of the arcs.
Could anyone find the answer for this?

Answers
Answer:
63cm
3 x 21 = 63
Answer: 63 cm
Step-by-step explanation: For every one cm deep, there is a further scale of 21 cm more. If the pond is 3 cm deep, then the scale would be 21 * 3, which is equivalent to 63.
Clayton sells computers. He makes $220 per week plus $50 for each computer he sells. He must make at least $770 per week.
How many computers must he sell to meet his needs?
Answers
Answer:
11 computers
Step-by-step explanation:
770 = 220 + 50x
770-220=550
550 = 50x
550/50
11=x
A cylindrical container 30cm in diameter holds approximately 30 litres of oil. how far does the oil level fall after 1 litre of oil has been used
Answers
The fall in the level of oil is 1.4147 cm when the total volume of oil consumed is 1 liter.
We assume the drop in the level of water to be d cm.
Since the container is cylindrical in shape, its volume is given as:
V = πr²h, where V is the volume, r is the radius, and h is the height.
In the question, we are given that the diameter of the can is 30 cm.
Hence its radius = 30/2 = 15 cm.
The capacity of the container is given to be 30 liters or 30*1000 = 30000 cm³.
The volume of the oil used = 1 liter or 1*1000 = 1000 cm³.
Thus, substituting V = 1000, r = 15, and h = d, in the formula of the volume, V = πr²h, we get:
1000 = π(15)²(d),
or, d = 1000/(225π) = 1.4147.
Thus, the fall in the water level is 1.4147 cm.
Therefore, the fall in the level of oil is 1.4147 cm when the total volume of oil consumed is 1 liter.
Learn more about the volumes of cylinders at
https://brainly.com/question/9554871
#SPJ4
what is the quotient?

Answers
Answer:
the answer is 4x \(10^{2}\)
Step-by-step explanation:
I hope this helps
have a nice day/night
Mark brainiest please
Answer:
First of all, a quotient is a number that the answer to a division number basically. So, I think the best answer would be the first choice: 4 times 10 with an exponent of 12. I think that is the correct answer.
help me im dying and i

Answers
Answer:
The better bar to buy is the Nutty Crunch
Step-by-step explanation:
4.74 / 6 = 0.79 per bar
7.80 / 10 = 0.78 per bar
:)
Answer:
Nutty Crunch is better
Step-by-step explanation:
write, but do not evalutate, an ittegral expression of the volume of the solid generated when r is roated about the horizantal line y=6
Answers
The integral expression of the volume of the solid generated when r is roated about the horizantal line y=6 is, V = π∫[f(y)]^2 dy
Let's consider the region bounded by the function r=f(y) and the horizontal line y=6 in the xy-plane, where r represents the distance between the y-axis and a point on a curve.
When this region is rotated around the horizontal line y=6, it generates a solid whose volume can be expressed as an integral in terms of y as follows:
V = π∫[f(y)]^2 dy
Here, the limits of integration are determined by the range of y-values for which the curve exists within the region bounded by the x-axis and the line y=6.
Note that we have not evaluated this integral yet since we do not have enough information about the specific function f(y).
Know more about volume of solid here:
https://brainly.com/question/20284914
#SPJ11
A Bar of steel is 340 cm long Issa cuts two 55cm lengths of the bar He then cuts the rest into as many 40cm lengths as possible Work out how many 40cm lengths of bar Issa cut.
Answers
Answer:
5 pieces of 40 cm
Step-by-step explanation:
A Bar of steel is 340 cm long Issa cuts two 55cm lengths of the bar
He then cuts the rest into as many 40cm lengths as possible
Work out how many 40cm lengths of bar Issa cut.
so
340cm - 55 cm - 55 cm = 230 cm remains
230 cm to cut into 40 cm as many as possible
40 cm
therefore, there are 5 pieces of 40 cm
I need help with this ( but I need to send another picture that has the answers )
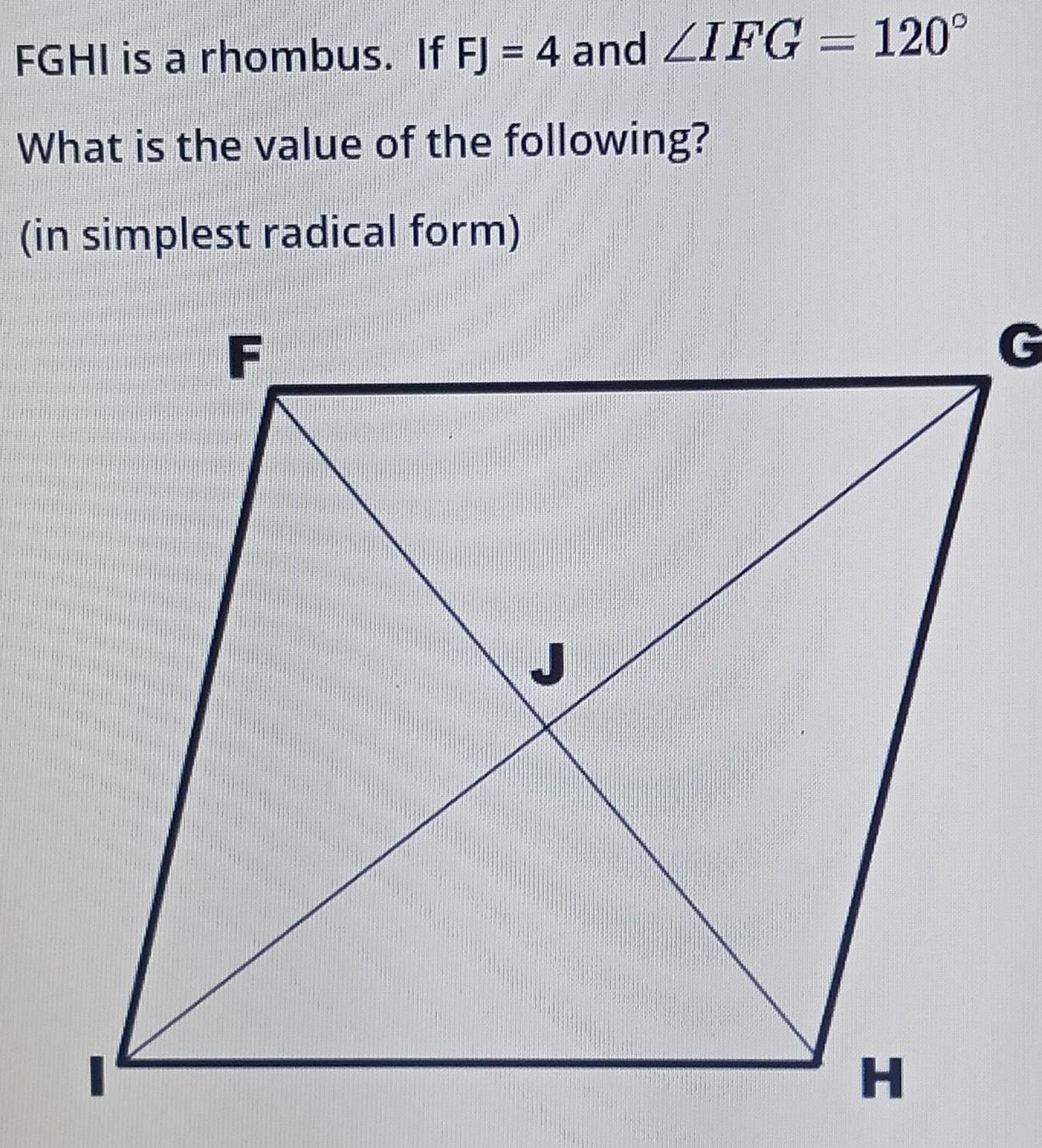

Answers
Step 1:
Draw the figure
The diagonals of a rhombus bisect each other,
therefore
FJ = JH
this implies that
JH = 4.
Opposite angles of a rhombus are equal, so
The diagonals of a rhombus bisect the interior angles.
Therefore,
\(\text{ angle JHG = }\frac{120^0}{2}=60^0\)The diagonals of a rhombus are perpendicular
\(\begin{gathered} Hence, \\ \cos 60^0=\frac{4}{GH} \\ \Rightarrow GH=\frac{4}{\cos60^0}=\frac{4}{\frac{1}{2}}=4\times2=8 \end{gathered}\)GH = 8 (b)
Also,
Using the Pythagorean rule,
\(\begin{gathered} JG^2+4^2=GH^2 \\ \Rightarrow JG^2+16=8^2 \\ \Rightarrow JG=\sqrt[]{64-16}=\sqrt[]{48}=4\sqrt[]{3}=6.928\text{ } \\ \text{right choice is C} \end{gathered}\)FH = FJ + JH
this implies that
FH = 4 + 4 = 8
FH = 8
right choice B
The diagonals of a rhombus bisect the interior angles.
therefore
\(\begin{gathered} angle\text{ JFG = }\frac{angle\text{ IFG}}{2}=\frac{120^0}{2}=60^0 \\ \text{ right choice is h} \end{gathered}\)Sum of the interior angles of a rhombus is 360degrees.
And opposite interior angles of a polygon are congruent.
Therefore
\(2(\text{angle FGH) +2(angle IFG) = 360degr}ees\)\(\begin{gathered} \text{this implies that} \\ 2(\text{angle FGH) = 360 - 2(angle IFG)} \\ \Rightarrow\text{angle FGH = 180 -angle IFG = 180 - 120= }60^0 \\ \text{ right choice is h} \end{gathered}\)\(\begin{gathered} \text{ but }FGJ\text{ = }\frac{FGH}{2}\text{ (diagonals bisect interior angles)} \\ \Rightarrow\text{FGJ =}\frac{60^0}{2}=30^0 \\ \text{right choice is j} \end{gathered}\)Also,
\(\begin{gathered} \(\begin{gathered} \text{JGH}=\text{ }\frac{FGH}{2}=\frac{60}{2}=30^0 \\ right\text{ choice is j} \end{gathered}\)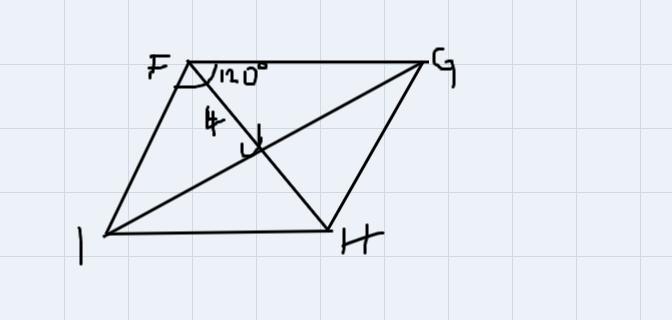
Translate the sentence into an inequality. Twice the difference of a number and 8 is greater than −21. Use the variable b for the unknown number.
Answers
Answer:
b > - 5/1Step-by-step explanation:
The statement
Twice the difference of a number and 8 is written as
2( b - 8)
The expression is greater than - 21 so we represent it by the > sign
So we have
2( b - 8) > - 21
Expand
2b - 16 > - 21
2b > - 21 + 16
2b > - 5
Divide both sides by 2
b > - 5/2Hope this helps you
Find the volume of the prism. (Image down below)

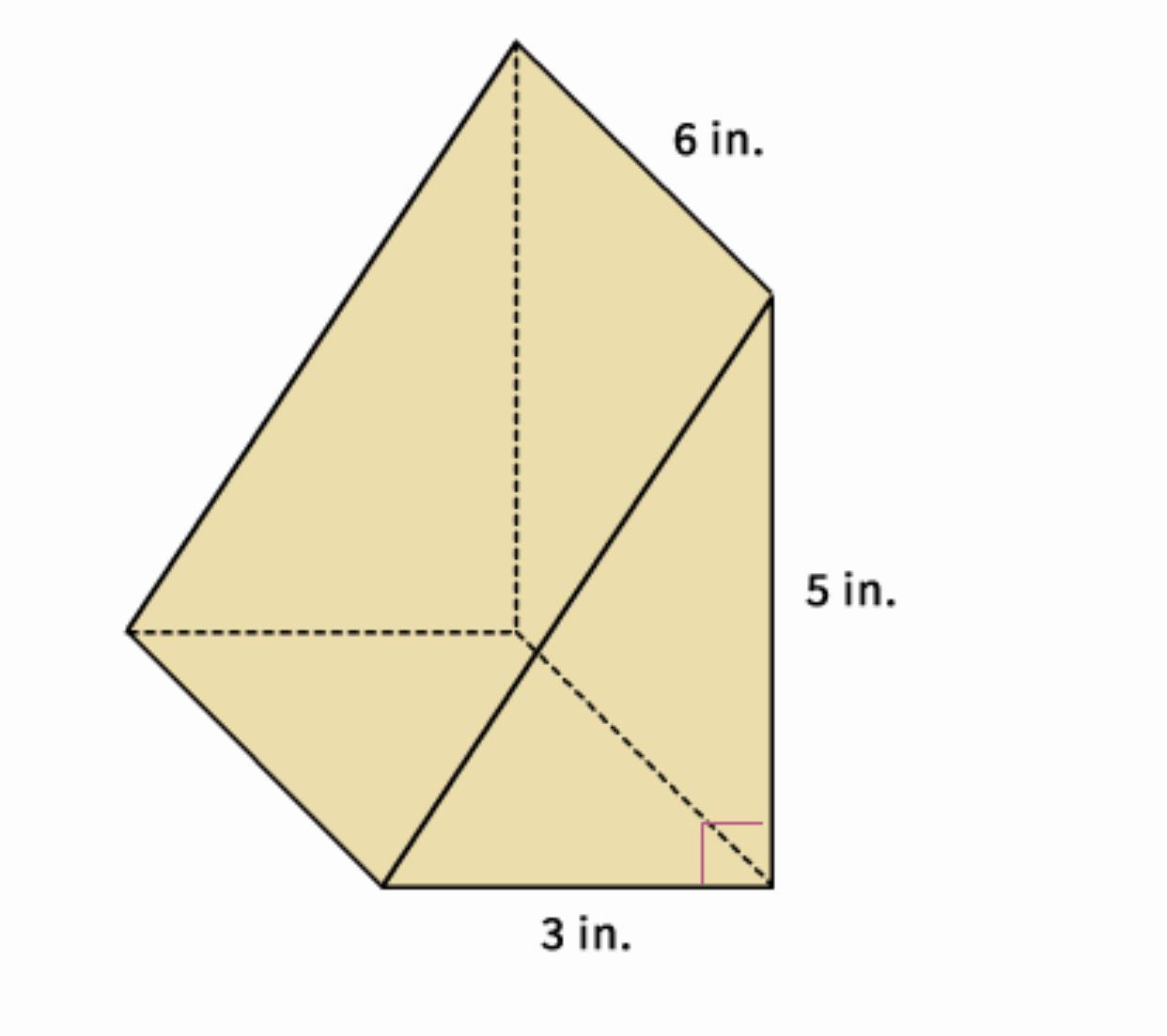
Answers
Answer:
Option (A)
Step-by-step explanation:
In the figure attached,
A prism has been given with two triangular bases.
If we put this prism with one of the triangular face as the base of the prism, height of the prism will be 6 in.
Volume of a prism is calculated with the formula,
Volume = (Area of the triangular base) × Height
Area of the triangular base = \(\frac{1}{2}(\text{Base})(\text{Height of the triangular base})\)
= \(\frac{1}{2}(3)(5)\)
= 7.5 in²
Volume of the prism = 7.5 × 6
= 45 in³
Therefore, Option (A) will be the answer.
Here is a list of 27 scores on a Statistics midterm exam: 20, 30, 31, 32, 46, 48, 49, 52, 54, 59, 61, 69, 71, 73, 74, 79, 81, 81, 81, 85, 86, 87, 88, 91, 94, 96, 97 Find Q2- Find Q1
Answers
The first quartile of the data set is 48.
Here is a list of 27 scores on a Statistics midterm exam: 20, 30, 31, 32, 46, 48, 49, 52, 54, 59, 61, 69, 71, 73, 74, 79, 81, 81, 81, 85, 86, 87, 88, 91, 94, 96, 97. Find Q2 and Q1.The median is the middle number of a data set arranged in ascending or descending order. There are 27 numbers in this data set. As a result, the median will be the 14th value when sorted in ascending order. The data set is given in ascending order. As a result, the median of the data set is 81. To find the first quartile or Q1 of this data set, the formula below will be used: Q1 = (n+1)/4th term Q1 = (27+1)/4th termQ1 = 7th terTo find the 7th term, the data set must be arranged in ascending order. The 7th term of the data set is 48.Therefore, the first quartile of the data set is 48.
Learn more about Quartile
brainly.com/question/17198478
#SPJ11
what number subtracted by 6, divided by 2, and added by 5 equals 9
Answers
Answer:
16
Step-by-step explanation:
What number subtracted by 6, divided by 2, and added by 5 equals 9
Step-by-step explanation:
x-6/2+5=9
x-6/2=9-5
x-6/2=4
x-6=4×2
x-6= 8
x=6+8
x=14
How long will it take to fill the pool if two hoses are used, one that fills at a rate of 40 gallons per hour and one that fills at a rate of 60 gallons per hour? 100 hours 150 hours 180 hours 200 hours.
Answers
It will take 180 Hours to fill the pool if both hoses are used.
In our question, one data is missing. You require the pool's volume or some information that enables you to calculate it. The same statement given by you is part of a problem where you know a series of data that shows the time required to fill the pool at different flow rates:
flow rate time
60 gal/h 300 h => 60 gal/h * 300 h = 18,000 gal
45 gal/h 400 h => 45 gal/h * 400 h = 18,000 gal
36 gal/h 500 h => 36 gal/h * 500 h = 18,000 gal
30 gal/h 600 h => 30 gal/h * 600 h = 18,000 gal
So for this pool to calculate (several times) that the volume is 18,000 gal.
You now possess two hoses, one of which has a flow rate of 40 gals per hour and the other of which has a flow rate of 60 gals per hour.
The total flow rate is the sum of the two flow rates"
total flow rate = 40 gal/h + 60 gal/h = 100 gal/h
And you just must divide the volume of the pool (18,000 gals) by the total flow rate (100 gal/h) to get the time to fill the pool:
time = volume / flow rate = 18,000 gal / 100 gal/h = 180 hours.
So, finally, our answer to fill the pool will be about 180 hours.
To know more about Volume, visit: https://brainly.com/question/23477586
#SPJ4
flow rate time
60 gal/h 300 h => 60 gal/h * 300 h = 18,000 gal
45 gal/h 400 h => 45 gal/h * 400 h = 18,000 gal
36 gal/h 500 h => 36 gal/h * 500 h = 18,000 gal
30 gal/h 600 h => 30 gal/h * 600 h = 18,000 gal
So for this pool to calculate (several times) that the volume is 18,000 gal.
You now possess two hoses, one of which has a flow rate of 40 gals per hour and the other of which has a flow rate of 60 gals per hour.
The total flow rate is the sum of the two flow rates"
total flow rate = 40 gal/h + 60 gal/h = 100 gal/h
And you just must divide the volume of the pool (18,000 gals) by the total flow rate (100 gal/h) to get the time to fill the pool:
time = volume / flow rate = 18,000 gal / 100 gal/h = 180 hours.
ASAP NEED HELP DUE TMR

Answers
!!HELP ME PLEASE!!
Which describes the graph of y = (x + 6)2 + 1?
A. Vertex at (−6, 1)
B. Vertex at (6, −1)
C. Vertex at (−6, −1)
D. Vertex at (6, 1)
Answers
Answer:
answers
Step-by-step explanation:
A. Vertex at (−6, 1)
You are running a fuel economy study. One of the cars you find is blue. It can travel 38 1/2 miles on 1 1/4 of gasoline. Another car is red. It can travel 21 3/5 on 4/5 of gasoline. What is the unit rate for miles per gallon for each car? Which car could travel the greater distance on 1 gallon of gasoline?
Answers
Answer:
Blue car: 30.8 miles per galon
Red car: 27 miles per galon
Blue car can travel longer distances on one galon!
Step-by-step explanation:
Blue car:
38 1/2=77/2=38.5 miles
1 1/4=5/4=1.25 gasoline
38.5/1.25=30.8miles per galon
Red car:
21 3/5=108/5=21.6 miles
4/5=0.8 gasoline
21.6/0.8=27 miles per galon
what are the terms a0, a1, a2, and a3 of the sequence {an}, where an equals a) 2n 1? b) (n 1)n 1? c) n/2? d) n/2 n/2?
Answers
When a\(_{n}\) = \(2^{n}\)+ n, a₀ = 1, a₁ = 3, a₂ = 6, and a₃ = 11
When a\(_{n}\) = n^(n+1)!, a₀ = 0, a₁ = 2, a₂ = 2⁶, and a₃ = 3²⁴
When a\(_{n}\) = [n/2], a₀ = 0, a₁ = 1/2, a₂ = 1, and a₃ = 3/2
When a\(_{n}\) = [n/2] + [n/2], a₀ = 0, a₁ = 1, a₂ = 2, and a₃ = 3/2
Number sequence
A number sequence is a progression or a list of numbers that are directed by a pattern or rule.
Here,
a₀, a₁, a₂, and a₃ are terms of a sequence
from option a, a\(_{n}\) = \(2^{n}\)+ n
⇒ a₀ = 2⁰+ 0 = 1+0 = 1
⇒ a₁ = 2¹+ 1 = 2+1 = 3
⇒ a₂, = 2²+ 2 = 4+2 = 6
⇒ a₃ = 2³+ 3 = 8 +3 = 11
from option b, a\(_{n}\) = n^(n+1)!
⇒ a₀ = 0^(0+1)! = 0
⇒ a₁ = 1^(1+1)! = 2² = 2
⇒ a₂, = 2^(2+1)! = 2^(3)! = 2⁶ [ ∵ 3! = 6 ]
⇒ a₃ = 3^(3+1)! = 3^(4)! = 3²⁴ [ ∵ 4! = 24 ]
from option c, a\(_{n}\) = [n/2]
⇒ a₀ = [0/2] = 0
⇒ a₁ = [1/2] = 1/2
⇒ a₂, = [2/2] = 1
⇒ a₃ = [3/2] = 3/2
from option d, a\(_{n}\) = [n/2] + [n/2]
⇒ a₀ = [0/2] + [0/2] = 0
⇒ a₁ = [1/2] + [1/2] = 1/2 + 1/2 = 1
⇒ a₂, = [2/2] + [2/2] = 1 + 1 = 2
⇒ a₃ = [3/2] + [3/2] = 6/4 = 3/2
Learn more about Number sequence problems at
https://brainly.com/question/28680939
#SPJ4
The Complete Question is -
What are the terms a₀, a₁, a₂, and a₃ of the sequence {a\(_{n}\)}, where a\(_{n}\) is where a\(_{n}\) equals
a. \(2^{n}\) + n b. n^(n+1)!
c. [n/2] d. [n/2] + [n/2]
A square has an area of
x^2-14x + 49cm2.
What is the perimeter of the square?
Answers
Answer:
Step-by-step explanation:
what is 672x787=___?
Answers
Answer:
528864
Step-by-step explanation:
Solve for x.
7.82x+1.83<15.42
Enter your answer in the boxes to correctly state the solution. Round your final answer to the nearest hundredth.
x
Answers
Answer:
26.44%
Step-by-step explanation:
The change in temperature is:
1535 - 1214 = 321
This change represents a percent increase:
321/1214*100% = 26.44% (rounded)
Yuson must complete 30 hours of community service. She does 2 hours each day. Which linear equation represents the hours Yuson has left after x days?
A.) y= -2x + 30
B.) y= 2x + 30
C.) y= -2x - 30
D.) y= 2x - 30
Answers
Answer:
A
Step-by-step explanation:
Because it's subtracting 2 hours every day, the slope is -2. Also because it's 30 hours, it's 30. Therefore: A.) y=-2x+30 is the answer.
Hopes this Helps!
Is this statement true or false?Why?Researchers conducted a study and obtained a p-value of 0.30. Because the p-value is quite high, there is evidence to accept the null hypothesis.
Answers
Researchers conducted a study and obtained the p-value is 0.30, which is higher than the common significance level of 0.05. This means that there is not enough evidence to reject the null hypothesis, but it does not mean that the null hypothesis is accepted.
Hence this statement is false.
When researchers conduct a study and obtain a p-value, they use it to make a decision regarding the null hypothesis.
However, a high p-value does not provide evidence to accept the null hypothesis.
Instead, it indicates that there is not enough evidence to reject the null hypothesis.
1. Researchers start with a null hypothesis (H0), which is a statement that there is no effect or relationship between variables being studied.
They also have an alternative hypothesis (H1), which is a statement that there is an effect or relationship between variables.
2. They collect data and perform statistical tests to calculate the p-value, which represents the probability of observing the test results (or more extreme results) assuming the null hypothesis is true.
3. The p-value is then compared to a pre-determined significance level (alpha), commonly set at 0.05 or 5%.
If the p-value is less than the significance level, researchers reject the null hypothesis in favor of the alternative hypothesis.
4. In this case, the p-value is 0.30, which is higher than the common significance level of 0.05.
This means that there is not enough evidence to reject the null hypothesis, but it does not mean that the null hypothesis is accepted.
5. Instead, researchers should say that they "fail to reject" the null hypothesis, meaning they cannot confidently conclude that the alternative hypothesis is true based on the data and analysis.
For similar question on researchers.
https://brainly.com/question/7965468
#SPJ11
1. five friends go to the movie theater together. (a) if there are 5 seats open in a row, how many ways can the friends choose seats? (b) if there are 7 seats open in a row, how many ways can the friends choose seats? (note that two seats will remain empty.) (c) repeat part (b), but where two of the friends are required to sit next to each other. (d) repeat part (b), but where two of the friends are required to not sit next to each other.
Answers
he number of ways the friends can choose seats without sitting next to each other is 7! - 4! = 5040
If there are 5 seats open in a row and no restrictions on the seating arrangement, each friend can choose one seat independently. Therefore, the total number of ways the friends can choose seats is 5 factorial (5!) which is equal to 5 × 4 × 3 × 2 × 1 = 120.
(b) If there are 7 seats open in a row and no restrictions on the seating arrangement, each friend can choose one seat independently. Therefore, the total number of ways the friends can choose seats is 7 factorial (7!) which is equal to 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040.
(c) If two friends are required to sit next to each other, we can treat them as a single entity. This reduces the problem to arranging four entities (three individual friends and one pair of friends) and three empty seats. The total number of ways the friends can choose seats is then 4 factorial (4!) which is equal to 4 × 3 × 2 × 1 = 24.
(d) If two friends are required to not sit next to each other, we can count the complement of the situation in part (c). There are 7 factorial (7!) total seating arrangements without any restrictions. From part (c), we found that there are 4 factorial (4!) seating arrangements where the two friends sit next to each other. - 24 = 5016.
Know more about arrangement here:
https://brainly.com/question/28406752
#SPJ11
Hey could u help me thankss

Answers
Answer:
B) 146 ≥ 9c+10
Step-by-step explanation:
$9 per yoga class can be represented with 9c, and then we have 9c+10 to represent the additional $10 yoga mat bought.
Since she can't use more than $146, then we have the inequality 9c+10≤146, which is the same as 146≥9c+10, so option B is correct.
Which parent function is represented by the table?
O A. f(x) = Ixl
B. f(x) = 2x
C. f(x) = x²
D. f(x) = x
x y
-2 -2
-1 -1
0
1
0
1
2 2

Answers
Answer:
D. f(x) = x
Step-by-step explanation:
You want the parent function described by a table that has its y-values equal to its x-values.
TableWe observe that each row of the table has the same value in the y-column as in the x-column. That is, ...
y = x
Written using function notation, this is ...
f(x) = x
#95141404393
The perimeter of a rectangle is 172 feet. Find the length and width if the length is an integer and the width is 2 times the next consecutive integer.
Answers
The length and width of the rectangle is 28 feet and 58 feet respectively.
How to find the sides of a rectangle?A rectangle is a quadrilateral with opposite sides equal to each other and opposite sides parallel to each other.
Therefore, the perimeter of a rectangle is the sum of the whole 4 sides of the rectangle.
Hence, the perimeter of a rectangle is 172 feet.
perimeter of a rectangle = 2(l + w)
where
l = lengthw = widthl = x
w = 2(x + 1) = 2x + 2
Therefore,
172 = 2(x + 2x + 2)
172 = 2(3x + 2)
divide both sides by 2
172 / 2 = 3x + 2
86 = 3x + 2
86 - 2 = 3x
3x = 84
divide both sides by 3
x = 84 / 3
x = 28
Therefore,
length = 28 feet
width = 2(28) + 2 = 58 feet
learn more on rectangle here: https://brainly.com/question/14656866
#SPJ1
I WILL GIVE BRAINLIEST
Dan’s dog-walking job pays $15 per hour. His job as a car-wash attendant pays $400 each week. Dan wants to know how many hours he needs to spend walking dogs to earn more than $520 in a week.
Which three inequalities can model this situation?
Select all the correct answers.
A. x(15 + 400) > 520
B. 520 < 400 + 15x
C. 15x > 120
D. 15x + 520 > 400
E. 520 < 15x + 400x
F. 15x + 400 > 520
Answers
\(\large\underline{\underline{\maltese{\purple{\pmb{\sf{\: Explanation :-}}}}}}\)
Let the number of hours be x for his job of Dog walking..
So, The equation would be:
\( \blue \dashrightarrow \green{ \sf15x +400}\)
Dan wants to earn more than $520 in a week, so this means that the expression is greater than 520:
\( \blue \dashrightarrow \green{ \sf15x + 400 > 520}\)
If we move the constant to the right-hand side and change its sign, The equation would be:
\( \blue \dashrightarrow \green{ \sf15x > 520 - 400} \\ \blue \dashrightarrow \green{ \sf15x > 120}\)
Also, the first inequality can be rearranged as:
\( \blue \dashrightarrow \green{ \sf520 < 400 + 15x}\)
URGENTT PLS ANSWER!!!!!
Mt.Whitney is the highest peak in California at 14,949 feet. The city of El Centro, also in California, is 39 feet below sea level. What is the difference in elevation between in Mt. Whitney’s peak and city of El Centro?
Answers
Answer:
14988 feet
Step-by-step explanation:
To find the difference, subtract.
14949 - (-39)
= 14949 + 39
= 14988
Use "add the opposite" to change "minus a negative" to "plus a positive"
Given P(A) =0.5 and P(B) =0.4 do the following.
(a) If A and B are mutually exclusive, compute P(A or B)
(b) If P(A and B) =0.3, compute P(A or B)
Answers
(a) The probability of either A or B occurring is 0.9.
(b) The probability of either A or B occurring when P(A and B) is 0.6.
Given that P(A) = 0.5 and P(B) = 0.4
(a) If A and B are mutually exclusive, compute P(A or B)
When two events A and B are mutually exclusive, it means that the occurrence of one event precludes the occurrence of the other event. That is, the two events have no common outcome.
Therefore, the probability of either A or B occurring is the sum of the probabilities of A and B.
This is denoted as P(A or B).
Hence, if A and B are mutually exclusive, the P(A or B) = P(A) + P(B) - P(A and B) [since P(A and B) = 0]
The probability of either A or B occurring is:P(A or B) = P(A) + P(B) - P(A and B)= 0.5 + 0.4 - 0= 0.9
(b) If P(A and B) = 0.3, compute P(A or B)
If A and B are not mutually exclusive, it means that the occurrence of one event does not preclude the occurrence of the other event.
That is, the two events have a common outcome.
Therefore, the probability of either A or B occurring is the sum of the probabilities of A and B, minus the probability of their intersection (common outcome).
This is denoted as P(A or B).Hence, if A and B are not mutually exclusive, P(A or B) = P(A) + P(B) - P(A and B)
The probability of either A or B occurring is:
P(A or B) = P(A) + P(B) - P(A and B)= 0.5 + 0.4 - 0.3= 0.6
Therefore, the probability of either A or B occurring when P(A and B) = 0.3 is 0.6.
Know more about the mutually exclusive,
https://brainly.com/question/12961938
#SPJ11