bryan has a bag containing 12 red marbles, 8 blue marbles, 5 green marbles, and 3 yellow marbles, he will randomly select one marble form the bag. what is the probability he will select a red marble?
Answers
You would add all the colors together which would be 28. The you would make a fraction and put the number of red marbles on top. Which would look like this: 12/28
Then you would simply 12/28 by 4 and you would get 3/7. Then if you need it in decimal form it would be 0.43
Related Questions
The expression 43πr3 represents the volume of a sphere, with radius r. Why is this expression a monomial?
Put responses in the correct input to answer the question. Select a response, navigate to the desired input and insert the response. Responses can be selected and inserted using the space bar, enter key, left mouse button or touchpad. Responses can also be moved by dragging with a mouse.
It is the product of a number, represented by Response area, and a variable with a whole number exponent, represented by Response area.
Question 2
What is the degree of the monomial?
The degree is
.
Answers
Degree of a polynomial is the highest power that its terms contain which is 3 in the given monomial.
What is a polynomial?They are mathematical expressions involving variables raised with non negative integers and coefficients(constants who are in multiplication with those variables) and constants with only operations of addition, subtraction, multiplication and non negative exponentiation of variables involved.
WE have been given an expression as 43πr³ represents the volume of a sphere, with radius r.
Terms can be added or subtracted to make a polynomial. They are composed of variables and constants all in multiplication.
So we know that if there is one term, then the polynomial will be called monomial.
Therefore, this expression is a monomial which have inly one term as 43πr³ .
Degree of a polynomial is the highest power that its terms contain which is 3 in the given monomial.
Learn more about polynomials here:
https://brainly.com/question/27343162
#SPJ1
Javon is helping his dad build a tree house. He has a piece of trim that is 11 feet long.
How many pieces can Javon cut that are 1 yard long?
How much of a yard will he have left over?
Answers
Answer:
Step-by-step explanation:
1 yard = 3 feet
11 feet * (1 yard)/(3 feet) =11/3 yards = 3⅔ yards
Javon can cut three one-yard pieces. ⅔ yard is left over.
Tomas has $1,000 to spend on a vacation. His
plane ticket costs $348.25. If he stays 5.5 days at
his destination, how much can he spend each
day? Write an inequality and then solve.
Inequality
Answers
1000 - 348.25 = 651.75
651.75 / 5.5 = 118.5 spendable per day
NO LINKS!! URGENT HELP PLEASE!!
1. Find the area of a regular octagon. Each side is 12 m.
2. The perimeter of a regular polygon is 72 feet. An exterior angle of the polygon measures 40°. Find the length of each side.
3. If the perimeter of a regular pentagon is 50 in. Find the area. Show a drawing and work please.
Answers
Answer:
1) 695.3 m²
2) 8 ft
3) 172.0 in²
Step-by-step explanation:
Question 1To find the area of a regular polygon, we can use the following formula:
\(\boxed{\begin{minipage}{5.5cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{s^2n}{4 \tan\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\end{minipage}}\)
Given the polygon is an octagon, n = 8.
Given each side measures 12 m, s = 12.
Substitute the values of n and s into the formula for area and solve for A:
\(\implies A=\dfrac{(12)^2 \cdot 8}{4 \tan\left(\dfrac{180^{\circ}}{8}\right)}\)
\(\implies A=\dfrac{144 \cdot 8}{4 \tan\left(22.5^{\circ}\right)}\)
\(\implies A=\dfrac{1152}{4 \tan\left(22.5^{\circ}\right)}\)
\(\implies A=\dfrac{288}{\tan\left(22.5^{\circ}\right)}\)
\(\implies A=695.29350...\)
Therefore, the area of a regular octagon with side length 12 m is 695.3 m² rounded to the nearest tenth.
\(\hrulefill\)
Question 2The sum of an interior angle of a regular polygon and its corresponding exterior angle is always 180°.
If the exterior angle of a polygon measures 40°, then its interior angle measures 140°.
To determine the number of sides of the regular polygon given its interior angle, we can use this formula, where n is the number of sides:
\(\boxed{\textsf{Interior angle of a regular polygon} = \dfrac{180^{\circ}(n-2)}{n}}\)
Therefore:
\(\implies 140^{\circ}=\dfrac{180^{\circ}(n-2)}{n}\)
\(\implies 140^{\circ}n=180^{\circ}n - 360^{\circ}\)
\(\implies 40^{\circ}n=360^{\circ}\)
\(\implies n=\dfrac{360^{\circ}}{40^{\circ}}\)
\(\implies n=9\)
Therefore, the regular polygon has 9 sides.
To determine the length of each side, divide the given perimeter by the number of sides:
\(\implies \sf Side\;length=\dfrac{Perimeter}{\textsf{$n$}}\)
\(\implies \sf Side \;length=\dfrac{72}{9}\)
\(\implies \sf Side \;length=8\;ft\)
Therefore, the length of each side of the regular polygon is 8 ft.
\(\hrulefill\)
Question 3The area of a regular polygon can be calculated using the following formula:
\(\boxed{\begin{minipage}{5.5cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{s^2n}{4 \tan\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\end{minipage}}\)
A regular pentagon has 5 sides, so n = 5.
If its perimeter is 50 inches, then the length of one side is 10 inches, so s = 10.
Substitute the values of s and n into the formula and solve for A:
\(\implies A=\dfrac{(10)^2 \cdot 5}{4 \tan\left(\dfrac{180^{\circ}}{5}\right)}\)
\(\implies A=\dfrac{100 \cdot 5}{4 \tan\left(36^{\circ}\right)}\)
\(\implies A=\dfrac{500}{4 \tan\left(36^{\circ}\right)}\)
\(\implies A=\dfrac{125}{\tan\left(36^{\circ}\right)}\)
\(\implies A=172.047740...\)
Therefore, the area of a regular pentagon with perimeter 50 inches is 172.0 in² rounded to the nearest tenth.
Answer:
1.695.29 m^2
2.8 feet
3. 172.0477 in^2
Step-by-step explanation:
1. The area of a regular octagon can be found using the formula:
\(\boxed{\bold{Area = 2a^2(1 + \sqrt{2})}}\)
where a is the length of one side of the octagon.
In this case, a = 12 m, so the area is:
\(\bold{Area = 2(12 m)^2(1 + \sqrt{2}) = 288m^2(1 + \sqrt2)=695.29 m^2}\)
Therefore, the Area of a regular octagon is 695.29 m^2
2.
The formula for the exterior angle of a regular polygon is:
\(\boxed{\bold{Exterior \:angle = \frac{360^o}{n}}}\)
where n is the number of sides in the polygon.
In this case, the exterior angle is 40°, so we can set up the following equation:
\(\bold{40^o=\frac{ 360^0 }{n}}\)
\(n=\frac{360}{40}=9\)
Therefore, the polygon has n=9 sides.
Perimeter=72ft.
We have
\(\boxed{\bold{Perimeter = n*s}}\)
where n is the number of sides in the polygon and s is the length of one side.
Substituting Value.
72 feet = 9*s
\(\bold{s =\frac{ 72 \:feet }{ 9}}\)
s = 8 feet
Therefore, the length of each side of the polygon is 8 feet.
3.
Solution:
A regular pentagon has five sides of equal length. If the perimeter of the pentagon is 50 in, then each side has a length = \(\bold{\frac{perimeter}{n}=\frac{50}{5 }= 10 in.}\)
The area of a regular pentagon can be found using the following formula:
\(\boxed{\bold{Area = \frac{1}{4}\sqrt{5(5+2\sqrt{5})} *s^2}}\)
where s is the length of one side of the Pentagon.
In this case, s = 10 in, so the area is:
\(\bold{Area= \frac{1}{4}\sqrt{5(5+2\sqrt{5})} *10^2=172.0477 in^2}\)
Drawing: Attachment

18
6+5e-0.1x
Let f(x) =
What is f(6)?
Enter your answer in the box rounded to the nearest tenth.
Answers
The value of function for x = 6 is f(6) = 2.1
Given that f(x) = \(18 / [ 6 + 5^{e-0.1x ]\)
We have to find the value of this function at x = 6.
f(6) =
\(18 / [ 6 + 5^{e-0.1 * 6} ] \\ \\ = 18 / [ 6 + 5^{e-0.6} ]\)
≈ 2.1
Therefore, f(6) = 2.1
Learn more about functions here -
brainly.com/question/12431044
#SPJ1

Answer:
2.1
Step-by-step explanation:

Given the following exponential function, identify whether the change represents
growth or decay, and determine the percentage rate of increase or decrease.
Y=38(1.09)^x
Answers
The exponential equation represents a growth, and the rate of increase is 9%.
Is it a growth or a decay?The general exponential equation is written as:
y = A*(1 + r)^x
Where A is the intial value, and r is the rate of growth or decay, depending of the sign of it (positive is growth, negative is decay).
Here we have:
y = 38*(1.09)^x
We can rewrite this as:
y = 38*(1 + 0.09)^x
So we can see that r is positive, thus, we have a growth, and the percentage rate of increase is 100% times r, or:
100%*0.09 = 9%
Learn more about exponential equations at:
https://brainly.com/question/11832081
#SPJ1
Charles drew a plan for a rectangular piece of material that he will use for a blanket. Three of the vertices are (−2.2,−2.3), (−2.2,1.5), and (1.5,1.5). What are the coordinates of the fourth vertex?
Answers
The coordinates of the fourth vertex are (-2.2, 1.5).
Understanding how to estimate coordinatesTo find the coordinates of the fourth vertex, we can use the fact that opposite sides of a rectangle have equal length and are parallel to each other.
First, we can find the length of one of the sides of the rectangle. Let's take the side connecting the points (-2.2, -2.3) and (-2.2, 1.5):
length = |1.5 - (-2.3)| = 3.8
Since this is a rectangle, the length of the side opposite to this one must also be 3.8. We can find this side by taking the points (-2.2, 1.5) and (1.5, 1.5):
width = |1.5 - (-2.2)| = 3.7
Now we know the length and width of the rectangle, so we can find the coordinates of the fourth vertex. Let's call this point (x, y).
Since the fourth vertex is opposite to the point (-2.2, -2.3), the x-coordinate of the fourth vertex must be the same as the x-coordinate of (-2.2, -2.3):
x = -2.2
Similarly, since the fourth vertex is opposite to the point (1.5, 1.5), the y-coordinate of the fourth vertex must be the same as the y-coordinate of (1.5, 1.5):
y = 1.5
Learn more about coordinates here:
https://brainly.com/question/17206319
#SPJ1
Plllzzzz answer this question, if Ronny when 68 miles per hour in his Tesla sports, how long will it be till he gets to his brother's house, his house is 92 miles from him consider- ring the fact that his wheel popped and lost two hours fixing it since he simply could not go that fast he, reduced his speed by 20 mph, how long will it take him to show up.
yes this is on my test
Answers
Answer:
the class has 12 girls and 16 boys what is the ratio of the total students to boys in simplest form
The following data give the estimated prices of a 6-ounce can or a 7.06-ounce pouch of water-packed tuna for 14 different brands, based on prices paid nationally in supermarkets. 1.04 1.95 1.23 0.83 0.70 0.48 1.45 1.14 0.58 0.64 0.69 0.63 0.62 0.67 Find the range. Find the sample variance. (Round your answer to four decimal places.) Find the sample standard deviation. (Round your answer to three decimal places.)
Answers
For the given data, the range, variance, and standard deviation is 1.47, 0.1716, and 0.414, respectively.
To find the range, subtract the minimum value from the maximum value in the set of data. The minimum value is 0.48 and the maximum value is 1.95, so the range is: 1.95 - 0.48 = 1.47.
To find the sample variance, follow these steps.
1. Calculate the mean of the data set.
2. Subtract the mean from each value in the data set.
3. Take the summation of the squares of the result.
4. Divide the sample size minus 1.
Upon calculation, the sample variance is 0.1716.
Lastly, to find the sample standard deviation, take the square root of the sample variance: √0.1716. = 0.414.
Learn more about range here: https://brainly.com/question/24326172
#SPJ4
If a hotel has 126 rooms. 4 floors in all . Ok if 334 rooms have been cleaned how many are left to be cleaned
Answers
Answer:
170 rooms left to clean.
Step-by-step explanation:
If you are implying that there are 126 rooms for each floor of the 4 floors total.
Given the scenario that there are 126 rooms for each floor with 4 floors total with 334 of the rooms cleaned. The rooms left to clean are calculated by finding the difference between the total amount of rooms, and the rooms cleaned.
This relationship can be given by:
#total rooms - #cleaned rooms = #rooms left to clean.
The total rooms are found by multiplying the number of floors by the number of rooms on each floor: 126 × 4 = 504 rooms total.
Now we have all the variables needed, and can solve for the missing one:
(126×4) - (334) = #rooms left to clean
504 - 334 = 170 = #rooms left to clean
I WILL GIVE YOU 20 POINTS AND THE BRAINLYEST
all of the points in the picture are on the same line.
Find the slope on the like exain or show your reasoning
write and equation for the line.
find the values for A and B. Explain your reasoning.
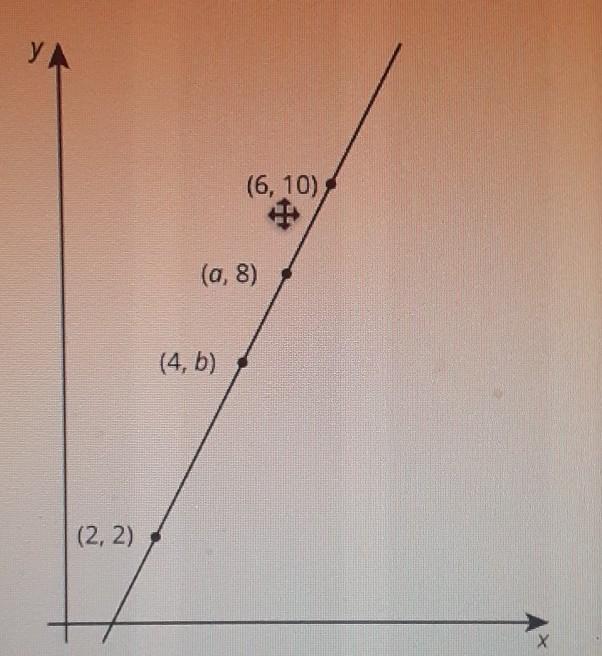
Answers
Answer/Step-by-step explanation:
✍️Slope of the line using two points, (2, 2) and (6, 10),
\( slope (m) = \frac{y_2 - y_1}{x_2 - x_1} = \frac{10 - 2}{6 - 2} = \frac{8}{4} = 2 \)
✍️To find the equation of the line in slope-intercept form, we need to find the y-intercept (b).
Substitute x = 2, y = 2, and m = 2 in y = mx + b, and solve for b.
2 = (2)(2) + b
2 = 4 + b
2 - 4 = b
-2 = b
b = -2
Substitute m = 2 and b = -2 in y = mx + b.
✅The equation would be:
\( y = 2x + (-2) \)
\( y = 2x - 2 \)
✍️To find the value of a, plug in (a, 8) as (x, y) into the equation of the line.
\( 8 = 2(a) - 2 \)
\( 8 = 2a - 2 \)
Add 2 to both sides
\( 8 + 2 = 2a \)
\( 10 = 2a \)
Divide both sides by 2
\( \frac{10}{2} = a \)
\( 5 = a \)
a = 5
✍️To find the value of b, plug in (4, b) as (x, y) into the equation of the line.
\( b = 2(4) - 2 \)
\( b = 8 - 2 \)
\( b = 6 \)
Please provide the correct answers! Be careful! Thank you! comment if you have questions. Look at photo.

Answers
The absolute maximum and minimum values obtained from the graph of the functions are;
Absolute maximum of g; [1, 4]
Absolute minimum of g; [4, -3]
Absolute maximum h; [4, 3]
Absolute minimum of h; (-4, -5)
What is the absolute maximum and minimum of a function?The absolute maximum and minimum of a function are the coordinates of the highest and lowest points on the graph of the function, within the specified domain.
The points on the graph of the functions indicates that the maximum and minimum values of the functions are;
Graph of g; Absolute maximum of g = (1, 4)
Absolute minimum of g ; [4, -3]
Graph of h
Absolute maximum of h; [4, 3]
Absolute minimum of h; (-4, -5)
Learn more on the absolute maximum of a function here: https://brainly.com/question/15358878
#SPJ1
A survey of 800 randomly selected adults in a certain country found that 82% believed that
protecting the rights of those with unpopular views is a very important component of a strong
democracy.
a. Verify the Central Limit Theorem conditions.
b. Find a 95% confidence interval for the proportion of adults in the country who believe that
protecting the rights of those with unpopular views is a very important component of a strong
democracy.
c. Would a 90% confidence interval based on this sample be wider or narrower than the 95%
interval? Give a reason for your answer.
Answers
a) the Central Limit Theorem conditions are met. b) The 95% confidence interval for the proportion of adults who believe in protecting the rights of those with unpopular views is approximately 0.7934 to 0.8466.
c) . A 90% confidence interval would be wider than the 95% interval
How to Verify the Central Limit Theorem conditions.To verify the Central Limit Theorem (CLT) conditions, we need to check the following:
1. Random Sampling: The survey states that 800 adults were randomly selected, which satisfies this condition.
2. Independence: We assume that the responses of one adult do not influence the responses of others. This condition is met if the sample is collected using a proper random sampling method.
3. Sample Size: To apply the CLT, the sample size should be sufficiently large. While there is no exact threshold, a common rule of thumb is that the sample size should be at least 30. In this case, the sample size is 800, which is more than sufficient.
Therefore, the Central Limit Theorem conditions are met.
b. To find a 95% confidence interval for the proportion of adults who believe in protecting the rights of those with unpopular views, we can use the formula for calculating a confidence interval for a proportion:
CI = p ± z * √(p(1-p)/n)
where:
- p is the sample proportion (82% or 0.82 in decimal form).
- z is the z-score corresponding to the desired confidence level. For a 95% confidence level, the z-score is approximately 1.96.
- n is the sample size (800).
Calculating the confidence interval:
CI = 0.82 ± 1.96 * √(0.82(1-0.82)/800)
CI = 0.82 ± 1.96 * √(0.82*0.18/800)
CI = 0.82 ± 1.96 * √(0.1476/800)
CI = 0.82 ± 1.96 * √0.0001845
CI ≈ 0.82 ± 1.96 * 0.01358
CI ≈ 0.82 ± 0.0266
The 95% confidence interval for the proportion of adults who believe in protecting the rights of those with unpopular views is approximately 0.7934 to 0.8466.
c. A 90% confidence interval would be wider than the 95% interval. The reason is that as we increase the confidence level, we need to account for a larger margin of error to be more certain about the interval capturing the true population proportion. As a result, the interval needs to be wider to provide a higher level of confidence.
Learn more about confidence interval at https://brainly.com/question/73194
#SPJ1
Help me out here pleaseeeeeeeeeeeeeeeeeee

Answers
Answer:
im 90% sure its A
Step-by-step explanation:
Which choices are equivalent to the expression below

Answers
Answer:
b and c for future help look up and equivalent calculator
What is the measure of each angle in the circle?
36°
40°
45°
60°

Answers
Answer:
45 degrees
Step-by-step explanation:
360 degrees is a whole circle, and there are 8 slots
360 / 8 = 45
Turn 8/6 into a mixed fraction
Answers
6/6 = 1
2/6 = 1/3
the mixed fraction is 1 1/3
see question above ^^

Answers
Solve
\(2 \times 2(3 \times 2) \\ hurry \: first \: person \: brainest \\ thank \: you\)
Pls
hurry
Thank you
Answers
Answer:
24
Step-by-step explanation:
2×2(3×2)
2×2(6)
2×12
24
80 people where asked why there favourite animal was
Answers
Answer:
need more to help solve your problem
Step-by-step explanation:
Solve the inequality |1-2x| -4 > -1
. Simplify all fractions as much as possible. Express your answer as an integer or fraction, and not as a decimal. If the answer is a fraction, provide the answer as "a/b". Do not leave spaces between characters.
x< ? or x> ?
Answers
Answer:
\(x < -3\text{ or }x > 3\)
Step-by-step explanation:
\(|1-2x|-4 > 1\\|1-2x| > 5\\\\1-2x > 5\\-2x > 6\\x < -3\\\\1-2x < -5\\-2x < -6\\x > 3\)
devide 60 in the ratio of 2:3
Answers
Answer:
Let the amounts be 2x and 3x.
Then 2x+3x=60
So, 5x=60
So, x=60/5=12
So, amounts are
2x=2*12=24
And 3x=3*12=36
Hope this helps you!
Step-by-step explanation:
Solution:
The two parts are 22+3
2
2
+
3
× 60 and 32+3
3
2
+
3
× 60
i.e., 25
2
5
× 60 and 35
3
5
× 60
i.e., 24 and 36
Which of the following would be true regarding the following exponential expression?
3m 7/9
A - The exponent of 3 is 7/9.
B - If written in radical form, 9 would be the exponent
inside the radicand.
C - The rational exponent is 9/7.
Report an Error
question 4 of 5
D - If written in radical form, 7 would be the index.
E - If written in radical form, 9 would be the index.
Answers
Answer:
A - The exponent of 3 is 7/9.
Step-by-step explanation:
The expression 3^(7/9) can be read as "3 to the power of 7/9".
This means that the number 3 is being multiplied by itself 7/9 times.
For example
3^(2/3) can be written as cube root of 3, cube root of 3 is equal to 3^(1/3) .
When the exponent of an expression is a fraction, it can be written in radical form, with the denominator of the fraction as the index of the radical. However, it's not true in this case as the index is not 9 but 7.
So, the correct answer is A - The exponent of 3 is 7/9.
What
is an arithmetic sequence with a common difference of −2?
Answers
Answer:
An arithmetic sequence with a common difference of −2 is 20,18,16,14,12..
Step-by-step explanation:
An arithmetic sequence is a sequence of numbers in which the difference between consecutive terms is same. Here, the common difference is -2, which means that each term in the sequence is obtained by subtracting 2 from the previous term.
To find the arithmetic sequence with a common difference of -2, you can start with an first term and then subtract 2 successively to find the subsequent terms.
Let the initial term is 20. Subtracting 2 from 20, we get 18. Subtracting 2 from 18, we get 16. Continuing this pattern, we subtract 2 from each subsequent term to generate the sequence. The arithmetic sequence with a common difference of -2 starting from 20 is
20,18,16,14,12
In this sequence, each term is obtained by subtracting 2 from the previous term, resulting in a common difference of -2.
4D. Jenna has ten 50 coins, ten 100 coins and ten 20c coins.
She chooses three of these coins and adds them together to find the
total amount.
How many different total amounts could she get?
Answers
Answer:
10 different amounts
Step-by-step explanation:
50+50+50= 150
100+100+100= 300
20+20+20= 60
100+50+50= 200
100+100+50= 250
20+50+50= 120
20+20+50= 90
100+20+20= 140
100+100+20= 220
50+20+100= 170
What is the value of c?
a)4 units
b)5 units
c)6 units
d)7 units

Answers
The value of c in the triangle is (b) 5 units
Finding the value of c in the triangleFrom the question, we have the following parameters that can be used in our computation:
The right triangle
The length c is the hypotenuse of one of the triangles and can be calculated using the following Pythagoras theorem
c² = sum of squares of the legs
Using the above as a guide, we have the following:
c² = 3² + 4²
Evaluate
c² = 25
Take the square roots
c = 5
Hence, the hypotenuse of the right triangle is 5
Read more about right triangle at
https://brainly.com/question/2437195
#SPJ1
An education researcher would like to test whether 2nd graders retain or lose knowledge during the summer when they are presumably not in school. She asks nine 2nd graders to take a comprehension exam at the end of the school year (May), and then asks those same students to come back after the summer (late August) to retake a different but equivalent exam, to see if their level of comprehension has changed. Using the data below, test this hypothesis using an alpha level of .05.
May August
90 100
65 80
78 92
50 60
89 90
92 98
75 70
90 96
65 87
a) What is the appropriate test? Is it a one or two tailed test?
b) State the null hypothesis (in words and using means).
c) State the alternative hypothesis (in words and using means).
d) Find the critical value.
e) Calculate the obtained value by hand. What does your decision mean?
Answers
Answer:
See step by step explanation
Step-by-step explanation:
From the problem statement, we understand that we need to investigate if 2nd graders RETAIN OR LOSE knowledge comparing information concerning two different months, therefore we are going to find out if the information gives us enough evidence of a difference in the two groups
a) The test should be a two tail-test
Sample sizes are small ( n₁ = n₂ = 9 ) which means we have to use t-student test
b and c) Test Hypothesis:
For Null Hypothesis H₀, we establish that the two means are equal, which in this case means that the two samples´ means are equal. And as Hypothesis alternative Hₐ that the H₀ is not true, or that the samples mean are different.
Null Hypothesis H₀ x₁ - x₂ = 0 or x₁ = x₂
Alternative Hypothesis Hₐ x₁ - x₂ ≠ 0 or x₁ ≠ x₂
d) Significance level α = 0,05 then α/2 = 0,025
then t(c) with α/2 = 0,025 and degree of freedom
df = n₁ + n₂ - 2 df = 9 + 9 -2 df = 16
From t s-tudent table we find t(c) = 2,12
e) Calculating:
x₁ and σ₁
x₂ and σ₂
σₓ = [ ( n₁ - 1 )* σ₁² + ( n₂ - 1 )*σ₂² ]/ n₁ + n₂ - 2
Using a calculator:
x₁ = 77,11 σ₁ = 13,86
x₂ = 85,89 σ₂ = 12,74
σₓ = [ ( 8*(13,86)² + 8*( 12,74 )² ] / 16
σₓ = (8* 192,1) + 8* ( 162,31) / 16
σₓ = (1536,8 + 1298,48 ) / 16
σₓ = 177,205
t(s) = ( x₁ - x₂ ) /√ σₓ²/ n₁ + σₓ²/ n₂
t(s) = ( 77,11 - 85,89 )/ (177,205)²/n₁ + (177,205)²/n₂
t(s) = - 8,78 / √3489,07 + 3489,07
t(s) = -8,78 / 83,54
t(s) = - 0,11
Comparing t(s) and t(c)
|t(s)| < |t(c)|
0,11 < 2,12
t(s) is in the acceptance region. We accept H₀
I need someone to solve b ASAP please help

Answers
b) The 99% confidence interval for the population proportion is given as follows: (0.57, 0.68).
What is a confidence interval of proportions?A confidence interval of proportions has the bounds given by the rule presented as follows:
\(\pi \pm z\sqrt{\frac{\pi(1-\pi)}{n}}\)
In which the variables used to calculated these bounds are listed as follows:
\(\pi\) is the sample proportion, which is also the estimate of the parameter.z is the critical value.n is the sample size.The confidence level is of 99%, hence the critical value z is the value of Z that has a p-value of \(\frac{1+0.99}{2} = 0.995\), so the critical value is z = 2.575.
The parameters for this problem are given as follows:
\(n = 520, \pi = \frac{325}{520} = 0.625\)
Then the lower bound of the interval is given as follows:
\(0.625 - 2.575\sqrt{\frac{0.625(0.375)}{520}} = 0.57\)
The upper bound of the interval is given as follows:
\(0.625 + 2.575\sqrt{\frac{0.625(0.375)}{520}} = 0.68\)
More can be learned about the z-distribution at https://brainly.com/question/25890103
#SPJ1
the distance-time graph represents a journey made by joe
Answers
If the question is 1st image:-
Second image contains answer.
I hope it helps.


Simplify the expression. Write the answer without using negative exponents. Assume that the variable is restricted to those numbers for which the expression is defined.
−m−8m9
Answers
The simplified expression is m^1 or simply m.
To simplify the expression −m^(-8) * m^9 without using negative exponents, we can utilize the properties of exponents.
First, let's deal with the negative exponent. A negative exponent indicates that the term should be moved to the denominator. So, we can rewrite −m^(-8) as 1/m^8.
Now, we can simplify the expression further: 1/m^8 * m^9.
When multiplying terms with the same base, we add the exponents. In this case, we have m^(-8) * m^9, which becomes m^(-8 + 9) = m^1 = m.
Finally, multiplying 1/m^8 by m gives us (1/m^8) * m = 1/m^(8-1) = 1/m^7.
Therefore, the simplified expression is 1/m^7, where m is the variable restricted to those numbers for which the expression is defined. By eliminating the negative exponent and combining like terms, we've simplified the expression without using negative exponents.
for such more question on simplified expression
https://brainly.com/question/723406
#SPJ8