What is the radius of a circle with a diameter of 240 mm?
A) 76.43 mm
B) 480.00 mm
C)12.00 mm
D) 120.00 mm
Answers
The radius of a circle is half of its diameter so the radius of a circle with a diameter of 240 mm is 120.00 mm. Option D is the correct answer.
To find the radius of a circle with a given diameter, you can follow these steps:
Given that the diameter is 240 mm, divide it by 2 to obtain the radius. Recall that the radius is half the length of the diameter.
Radius = Diameter / 2
In this case, Radius = 240 mm / 2 = 120 mm.
Therefore, the radius of the circle with a diameter of 240 mm is 120.00 mm.
Learn more about Radius at
https://brainly.com/question/31224639
#SPJ4
Related Questions
h(x)=(32)x−1 the outputs
Answers
The possible outputs of the function for different values of [x] are given below.
What is a expression? What is a mathematical equation? What do you mean by domain and range of a function?A mathematical expression is made up of terms (constants and variables) separated by mathematical operators.A mathematical equation is used to equate two expressions. Equation modelling is the process of writing a mathematical verbal expression in the form of a mathematical expression for correct analysis, observations and results of the given problem.For any function y = f(x), Domain is the set of all possible values of [y] that exists for different values of [x]. Range is the set of all values of [x] for which [y] exists.Given is the following function -
h(x) = 32x - 1
We can write the output for the given function as -
[x] h(x) = 32x - 1 h(x)
1 {32 x 1 - 1 = 31} 31
2 {32 x 2 - 1 = 63} 63
3 {32 x 3 - 1 = 95} 95
4 {32 x 4 - 1 = 127} 127
Therefore, the possible outputs of the function for different values of [x] are given above.
To solve more questions on Equations, Equation Modelling and Expressions visit the link below -
brainly.com/question/14441381
#SPJ1
asap answer dont get it wrong


Answers
Answer:
B
Step-by-step explanation:
The parabola minimum is 3
The top quadratic minimum is 2 so
g(x) minimum is greater
Avery has two books and a lunch box in his backpack Each book weighs 7/8 pound. The total weight in his backpack it 2 2/3 pounds. How much does Avery's lunch box weigh?
Answers
The weight of the Avery's lunch box using given weights is equal to 0.92 pounds (rounded to two decimal places).
Total weight of the backpack= 2 2/3 pounds
= 8/3 pounds
The weight of the each book =7/8 pounds.
Let x be the weight of the lunch box in pounds.
An equation that represents the total weight in Avery's backpack,
2(7/8) + x = 8/3
To solve for x, simplify and solve for x,
⇒14/8 + x = 8/3
Multiplying both sides by 24 the least common multiple of 8 and 3 to clear the fractions,
⇒42 + 24x = 64
Subtracting 42 from both sides,
⇒24x = 22
Dividing both sides by 24,
⇒x = 22/24
Simplifying the fraction,
⇒x = 11/12
= 0.92 pounds (rounded to two decimal places).
Therefore, the weight of the lunch box is equal to 0.92 pounds (rounded to two decimal places).
learn more about weight here
brainly.com/question/14315665
#SPJ4
Let theta be an acute angle of a right triangle. Find the values of the other five trigonometric functions of theta.

Answers
The exact values of the remaining trigonometric functions are listed below:
Case 3: cos θ = 3 / 5, tan θ = 4 / 3, cot θ = 3 / 4, sec θ = 5 / 3, csc θ = 5 / 4
Case 4: sin θ = √11 / 6, tan θ = √11 / 5, cot θ = 5√11 / 5, sec θ = 6 / 5, csc θ = 6√11 / 11
Case 5: cos θ = 8√73 / 73, sin θ = 3√73 / 73, tan θ = 3 / 8, cot θ = 8 / 3, csc θ = √73 / 3
Case 6: sin θ = 1 / 2, cos θ = √3 / 2, tan θ = √3 / 3, sec θ = 2√3 / 3, csc θ = 2
How to find the exact values of trigonometric functions
In this problem we find four cases of trigonometric functions, whose exact values of remaining trigonometric functions must be found. The trigonometric functions are defined below:
sin θ = y / √(x² + y²)
cos θ = x / √(x² + y²)
tan θ = y / x
cot θ = x / y
sec θ = √(x² + y²) / x
csc θ = √(x² + y²) / y
Now we proceed to determine the exact values of the trigonometric functions:
Case 3: y = 4, √(x² + y²) = 5
x = √(5² - 4²)
x = 3
cos θ = 3 / 5
tan θ = 4 / 3
cot θ = 3 / 4
sec θ = 5 / 3
csc θ = 5 / 4
Case 4: x = 5, √(x² + y²) = 6
y = √(6² - 5²)
y = √11
sin θ = √11 / 6
tan θ = √11 / 5
cot θ = 5√11 / 5
sec θ = 6 / 5
csc θ = 6√11 / 11
Case 5: x = 8, √(x² + y²) = √73
y = √(73 - 8²)
y = 3
cos θ = 8√73 / 73
sin θ = 3√73 / 73
tan θ = 3 / 8
cot θ = 8 / 3
csc θ = √73 / 3
Case 6: x = √3, y = 1
sin θ = 1 / 2
cos θ = √3 / 2
tan θ = √3 / 3
sec θ = 2√3 / 3
csc θ = 2
To learn more on trigonometric functions: https://brainly.com/question/25618616
#SPJ1
I REALLY NEED THE HELP FAST AND CORRECTLY PLEASE
What is the quotient of the complex numbers below?
7 + i/3-i
Answers
Answer:
I think it's 7- 2i over 3. hopefully that helps
a differentiable function ff has the property that f′(x)≤3f′(x)≤3 for 1≤x≤81≤x≤8 and f(5)=6f(5)=6. which of the following could be true?
Answers
If a differentiable function ff has the property that f′(x)≤3f′(x)≤3 for 1≤x≤81≤x≤8 and f(5)=6f(5)=6, then f(1) can be true when its value is -6. Option (C) is correct.
Given that a differentiable function f has the property that
f′(x)≤3f′(x)≤3 for 1≤x≤8 and f(5)=6.
We need to determine which of the following could be true.
As per the question, a differentiable function f has the property that f′(x)≤3f′(x)≤3 for 1≤x≤8 and f(5)=6.
So, integrating f′(x)≤3f′(x)≤3
we get,
f(x) ≤3x + C ……(1)
Differentiating (1) w.r.t. x,
we get,
f′(x) ≤3 …..(2)
Now, we can say that f′(x) is maximum when f′(x) =3
From (2),
we get that the function f(x) increases continuously from left to right and there are no minima.
So, the value of f(1) can be minimum when f(x) is minimum i.e. when x=1
So, f(1) ≤3 + C …. (3)
Also, as per the question, f(5)=6Substitute x=5 in (1),
we get,f(5) ≤3*5 + C ….. (4)
Substitute f(5) = 6 in (4),
we get,
6 ≤3*5 + C or C ≥ -9
Now substitute C ≥ -9 in (3),
we get,
f(1) ≤ 3 - 9 = -6
Option (C) is correct.
learn more about differentiable function
https://brainly.com/question/1164377
#SPJ11
2cm + 5cm + 6.4cm cuboid
Answers
Answer:
64 volume of the cuboid
formula used is lbh multiplies together.
Mark me as brainliest
Hope it helps:)
Step-by-step explanation:
Adrian bought a car worth $12000 on 36 easy installments of $375. Answer the following questions. (1) How much total amount did Adrian pay in 36 months? Answer: Total payment A = $ (2) Identify the letters used in the simple interest formula I = Prt. I= $ P= $ and t years. (3) Find the rate of interest in percentage. Answer: r %. ASK YOUR TEACHER
Answers
3) since we don't have the information about the interest paid (I), we cannot determine the rate of interest at this time.
(1) To find the total amount Adrian paid in 36 months, we can multiply the monthly installment by the number of installments:
Total payment A = Monthly installment * Number of installments
= $375 * 36
= $13,500
Therefore, Adrian paid a total of $13,500 over the course of 36 months.
(2) In the simple interest formula I = Prt, the letters used represent the following variables:
I: Interest (the amount of interest paid)
P: Principal (the initial amount, or in this case, the car worth)
r: Rate of interest (expressed as a decimal)
t: Time (in years)
(3) To find the rate of interest in percentage, we need more information. The simple interest formula can be rearranged to solve for the rate of interest:
r = (I / Pt) * 100
To know more about Number visit:
brainly.com/question/3589540
#SPJ11
On a coordinate plane, 3 parallelograms are shown. Parallelogram A B C D has points (3, 5), (6, 5), (4, 1), (1, 1). Parallelogram A prime B prime C prime D prime has points (3, negative 5), (6, negative 5), (4, negative 1), (1, negative 1). Parallelogram A double-prime B double-prime C double-prime D double-prime has points (negative 3, negative 4), (0, negative 4), (negative 2, 0), (negative 4, 0).
Which rule describes the composition of transformations that maps pre-image ABCD to final image A"B"C"D"?
Reflection across the x-axis composition translation of negative 6 units x, 1 unit y.
Translation of negative 6 units x, 1 unit y composition reflection across the x-axis.
90 degree rotation about point 0 composition translation of negative 6 units x, 1 unit y.
Translation of negative 6 units x, 1 unit y composition 90 degree rotation about point 0.
Answers
Translation of negative 6 units x, 1 units y composition reflection across the x-axis
The composition transformation that maps ABCD to A''B''C''D'' comprises
of two or more transformations that maps the image
The rule that describes the composition transformation that maps ABCD to
A''B''C''D'' is the option;
Translation of negative 6 units x, 1 units y composition reflection across the x-axis.
The given coordinates of parallelogram ABCD are (3, 5), (6, 5), (4, 1), (1, 1)
The coordinates of the parallelogram A'B'C'D' are; A'(3, -5), B'(6, -5), C'(4, -1), D(1, -1)
The coordinates of the parallelogram A''B''C''D'' are;
D(-5, 0), C''(-2, 0), A''(-3, -4), B''(0, -4)
The image of the point (x, y), following a reflection about the x-axis is the point (x, -y)
The difference in the coordinates of the parallelogram ABCD and A'B'C'D'
is the change in the sign of the y-coordinates
Therefore, the transformation that gives the parallelogram A'B'C'D' from
the parallelogram ABCD is a reflection about the x-axis
The difference between the coordinates of the vertices of the
parallelogram A'B'C'D' and the parallelogram A''B''C''D'', is a change in the
x-value by (-6), and a change in the y-value by (+1)
Therefore, the parallelogram A''B''C''D'' can be obtained from parallelogram
A'B'C'D', by a translation of -6 units (left) in the x-direction and a translation
of 1 unit, x in the y-direction
Which gives;
The composition transformation that maps the pre-image ABCD to the
final image A''B''C''D'', (given that in a composition transformation, the
transformation to the right is done first) are;
\($\mathrm{T}_{-6,1} \cdot \mathrm{r}_{\mathrm{x}-\{axis}}(\mathrm{x}, \mathbf{y})$\)which is the option;
Translation of negative 6 units x, 1 units y composition reflection across the x-axis
Learn more about composition transformation visit here:
brainly.com/question/15832612
#SPJ1

find the probability that the data value will be more extreme than 3.65 standard deviations from the mean.
Answers
The probability of the data vale more extreme than 3.65 is 0.000131.
First of all given that x(value) = μ+3.65σ , where μ is the mean and σ is the standard deviation.
we know that z-score = (x - μ)/σ
z-score = (μ+3.65σ - μ)/σ
z = 3.65σ/σ
z = 3.65
From the normal distribution table,
P(z>3.65) = 0.000131
To know more about probability
https://brainly.com/question/18651306
#SPJ4
I need help please thank you

Answers
Answer:
question 1 would be A because the answer are expanded brackets
factor the following 6x^2-11x+4
Answers
Answer:
(2x-1) (3x-4)
Step-by-step explanation:
Answer:
Step-by-step explanation:
(3x -4)(2x - 1)
ERROR ANALYSIS Describe and correct the error in solving the equation.
❌ 2(x+1)²+3=21
2(x+1)²=18
(x+1)²=9
x+1=3
x=2
Answers
Answer:
see explanation
Step-by-step explanation:
the error is in the line x + 1 = 3 , that is
2(x + 1)² + 3 = 21 ( subtract 3 from both sides )
2(x + 1)² = 18 ( divide both sides by 2 )
(x + 1)² = 9 ( take square root of both sides )
x + 1 = ± \(\sqrt{9}\) = ± 3 ← note ±
subtract 1 from both sides
x = - 1 ± 3
Then
x = - 1 - 3 = - 4 , or
x = - 1 + 3 = 2
That is a quadratic equation has 2 solutions
for which (if any) of the three dependent variables in this data set (gender, age, ethnicity) would you report the standard deviation?
Answers
Gender and ethnicity are categorical variables and therefore, the standard deviation cannot be calculated for variables.
The standard deviation is a measure of the spread or dispersion of the data around the mean. In other words, it tells us how far each data point in a set is from the average of the set.
When we analyze data, it's important to understand how much variation there is in the data, and the standard deviation is one way to do this.
When it comes to the three dependent variables in the data set (gender, age, and ethnicity), it is important to understand that the standard deviation is only calculated for numerical data.
However, age is a numerical variable, and the standard deviation can be calculated for it.
To find the standard deviation of the ages, we need to first find the mean of the ages and then subtract each age value from the mean and square the result.
Next, we add up all the squared deviations and divide by the number of ages minus one. Finally, we take the square root of the result, and that gives us the standard deviation of the ages in the data set.
To know more about standard deviation here.
https://brainly.com/question/16555520
#SPJ4
60in what is the area
Answers
Answer:
wdym 60 inches measures length (?????)
Answer:
Area = Side2
Step-by-step explanation:
If cos x = sin(20 + x) and 0° < x < 90°, the value of xis
Answers
Answer:
x= 35
Step-by-step explanation:
Cos x = Sin( 20+x)
Sin ( 90 – x) = Sin(20+x)
90 – x = 20+x
2x = 70
x = 35
A company is looking to hire a lawyer. One law rm states that their legal fees can be determined using the
expression 350x + 22,000, where x is the number of hours of legal assistance. A second law rm states that their legal
fees can be determined using the expression 410x+16,000. The company president wants to know when the legal fees
would cost the same for each law rm. What number of hours of legal assistance makes the equation 350x+22,000 =
410x+16,000 true?
Answers
Answer:
100 hours
Step-by-step explanation:
Law firm A = 350x + 22,000,
Law firm B = 410x+16,000
Where,
x = number of hours of legal assistance
What number of hours of legal assistance makes the equation 350x+22,000 = 410x+16,000 true?
Equate the legal fees of the two law firms
350x + 22,000 = 410x + 16,000
Collect like terms
350x - 410x = 16,000 - 22,000
-60x = -6,000
Divide both sides by -60
x = -6,000 / -60
= 100
x = 100 hours
The number of hours of legal assistance makes the equation true is 100 hours
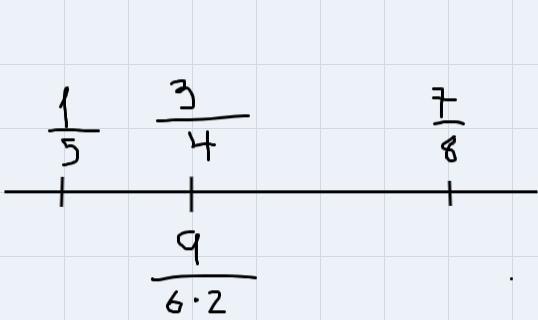
Fractions least to highest. The numbers can only be used once and it is from 1-9. Any help?

Answers
There are two fractions that are equal, but one of them has a product in the denominator. We need to choose 3 numbers such that the simplified fraction lead to two different numbers. Those numbers are:
\(\frac{9}{6\cdot2}=\frac{3}{4}\)Then, there are 4 more numbers: 1, 5, 7, and 8. 1/5 is lower than 3/4, and 7/8 is higher than 3/4. Then, the answer is:
12 + 4r-9= 9x + 7 - 5x
Answers
Answer:
-2x+4r = 4 i think
Step-by-step explanation:
what are the statements and reasons for 19 and 20?? pls help i will mark brainliest!!! 35 points ^^

Answers
1. The proof is completed using transitive property as follows
Statement Reason
c || d Given
∠ 1 ≅ ∠ 2 Given
∠ 1 ≅ ∠ 3 Corresponding angles
∠ 2 ≅ ∠ 3 Alternate exterior angles
∠ 4 + ∠ 3 = 180 Definition of supplementary angles
∠ 4 + ∠ 2 = 180 Substitution property of equality
2.
The second proof is achieved using transitive property
Statement Reason
∠ 1 + ∠ 2 = 180 Given
∠ 4 ≅ ∠ 5 Given
∠ 4 ≅ ∠ 5 Alternate interior angles are equal (s || r).
linear pair of ∠ 1 ≅ ∠ 2 Corresponding angles are equal (s || q)
q || r || s Transitive property
What is Substitution property of equality?The substitution property of equality is a fundamental principle in mathematics that states that if two quantities or expressions are equal, then one can be substituted for the other in any equation, inequality, or expression without changing the truth or validity of the statement.
This helped us to complete the proof, knowing that ∠ 2 ≅ ∠ 3 (Alternate exterior angles are equal) the we can substitute 2 for 3. so we have that
∠ 4 + ∠ 3 = 180
∠ 4 + ∠ 2 = 180
Learn more about Substitution property of equality at
https://brainly.com/question/16846643
#SPJ1
What is -x-y=5 in function form solving for y
Answers
Answer:
f(x) = - x - 5
Step-by-step explanation:
- x - y = 5 ( multiply through by - 1 )
x + y = - 5 ( subtract x from both sides )
y = - x - 5 , that is
f(x) = - x - 5
(2x+1)(z-7) = 2711
2x+1
11(x-7)
O A. All real numbers except 7
O B. All real numbers except - 1/2
C. All real numbers except - and 7
O
O D. All real numbers
Answers
Select each expression that is equivalent to 3/16 if x=34 . 2x+116 x2−616 (38)2÷x x−14 2x−x2−34 HELPPPP
Answers
Given statement solution:- None of the expressions evaluated are equivalent to 3/16 when x=34.
Let's evaluate each expression to determine if it is equivalent to 3/16 when x=34:
2x+116:
Substituting x=34, we have: 2(34) + 116 = 68 + 116 = 184
184 is not equal to 3/16.
\(x^2\) - 616:
Substituting x=34, we have: \((34)^2\) - 616 = 1156 - 616 = 540
540 is not equal to 3/16.
\((38)^2\)÷ x:
Substituting x=34, we have:\((38)^2\) ÷ 34 = 1444 ÷ 34 = 42.47 (approx.)
42.47 is not equal to 3/16.
x - 14:
Substituting x=34, we have: 34 - 14 = 20
20 is not equal to 3/16.
2x -\(x^2\)- 34:
Substituting x=34, we have: 2(34) - \((34)^2\) - 34 = 68 - 1156 - 34 = -1122
-1122 is not equal to 3/16.
None of the expressions evaluated are equivalent to 3/16 when x=34.
For such more questions on Equivalent Expressions
https://brainly.com/question/15775046
#SPJ11
6. an economics researcher wants to estimate the mean number of hours worked by all grocery store employees in the county. how many employees must be included in the sample to be 95% confident that the sample mean is within 1.5 hours of the population mean? a previous study showed that the population standard deviation is 7.9. the critical value for a level of confidence of 95% is 1.96.
Answers
The number of employees that must be included in the sample to be 95% confident that the sample mean is within 1.5 hours of the population mean is 107 employees.
To estimate the mean number of hours worked by all grocery store employees in the county with 95% confidence and a margin of error of 1.5 hours, we can use the sample size formula:
n = (Z * σ / E)²
where:
- n is the required sample size
- Z is the critical value (1.96 for a 95% level of confidence)
- σ is the population standard deviation (7.9 from the previous study)
- E is the margin of error (1.5 hours)
Plugging in the given values:
n = (1.96 * 7.9 / 1.5)²
n ≈ 106.56
Since you cannot have a fraction of an employee, you need to round up to the nearest whole number. Therefore, the researcher must include 107 employees in the sample to be 95% confident that the sample mean is within 1.5 hours of the population mean.
Learn more about sample size here: https://brainly.com/question/29766751
#SPJ11
5 cars enter the mall parking lot every 5 minutes.
a. How many cars enter the parking lot in 10 minutes?
b. How many cars enter the parking lot in 25 minutes?
Answers
Answer:
Step-by-step explanation:
2 x 5=10
5x5=25
a=10
b=25
Let X1and X2 be independent random variables with normal distributions N(6,1) and N(7,1), respectively. Find P(X 1>X 2). Write P(X1>X 2)=P(X 1−X 2 >0) and determine the distribution of X 1−X 2
Answers
By reframing the problem as P(X1 - X2 > 0) and using the properties of independent normal random variables, we determine that the distribution of X1 - X2 is N(-1, 2). The probability P(X1 > X2) is 0.3085.
To find the probability that X1 is greater than X2, we can reframe the problem as finding the probability that X1 - X2 is greater than 0. This allows us to determine the distribution of the random variable X1 - X2. Given that X1 and X2 are independent random variables with normal distributions N(6,1) and N(7,1) respectively, we can calculate the probability P(X1 - X2 > 0) and determine the distribution of X1 - X2.
To find P(X1 > X2), we reframe it as P(X1 - X2 > 0). The difference between X1 and X2, denoted as X1 - X2, follows a normal distribution with mean μ1 - μ2 and variance σ\(1^2\) + σ\(2^2\) since X1 and X2 are independent normal random variables. In this case, μ1 = 6, μ2 = 7, σ\(1^2\) = 1, and σ\(2^2\) = 1.
The distribution of X1 - X2 is N(μ1 - μ2, σ\(1^2\) + σ\(2^2\)), which is N(6 - 7, 1 + 1) = N(-1, 2). We now need to calculate the probability P(X1 - X2 > 0) using the distribution N(-1, 2).
To do this, we can standardize the distribution by subtracting the mean and dividing by the standard deviation. Standardizing gives us P((X1 - X2 - (-1))/\(\sqrt{(2)}\) > (0 - (-1))/\(\sqrt{(2)}\)), which simplifies to P((X1 - X2 + 1)/\(\sqrt{(2) }\)> 1/\(\sqrt{(2)}\)).
We can now use the standard normal distribution table or a calculator to find the probability that a standard normal random variable is greater than 1/\(\sqrt{(2)}\). This probability is approximately 0.3085.
Therefore, P(X1 > X2) or P(X1 - X2 > 0) is approximately 0.3085.
In summary, by reframing the problem as P(X1 - X2 > 0) and using the properties of independent normal random variables, we determine that the distribution of X1 - X2 is N(-1, 2). The probability P(X1 > X2) is approximately 0.3085.
Learn more about standard deviation here:
https://brainly.com/question/29115611
#SPJ11
Keith buy 3 yard of material to make a blanket. He trim off a total of 1/6 yard before he begin ewing. How much material remain for the blanket?
Answers
The material remained for the blanket after trimming off by Keith is 2.5 yards.
Simple subtraction and multiplication can provide the result. Beginning will be by the multiplication. Firstly finding the exact amount of material trimmed = 3×1/6
Performing multiplication and division on Right Hand Side of the equation
Trimmed material = 1/2 or 0.5
Now, we need to subtract the trimmed material from overall amount of material
Remaining material = 3 - 0.5
Performing subtraction on Right Hand Side of the equation
Remaining material = 2.5 yards
Hence, 2.5 yards of material remained.
Learn more about multiplication -
https://brainly.com/question/10873737
#SPJ4
an investment of $1000 earns 6% annual interest, compounded monthly. how much money would you have after 20 years
Answers
Answer:
The answer is 14,400
Step-by-step explanation:
A candy store allows customers to select 3 different candies to be packaged and mailed. If there are 13 varieties available, how many possible selections can be made?
Answers
There are 286 different possible selections of three candies from 13 varieties.
To find out how many possible selections can be made, we can use the combination formula: nCk = n! / (k! (n-k)!), where n is the total number of candies available and k is the number of candies to be selected.
In this case, n = 13 (the number of candy varieties) and k = 3 (the number of candies to be selected). So the number of possible selections can be calculated as follows: 13C3 = 13! / (3! (13-3)!) = 286. Therefore, there are 286 different possible selections of three candies from the 13 varieties available in the candy store.
Learn more about combination here:
https://brainly.com/question/28720645
#SPJ11
The probability that X is a 2, 11, or 12 is:
a.) 1/36
b.) 2/36
c.) 3/36
d.) 4/36
Answers
Answer:
The correct answer is c.) 3/36.There are three favorable outcomes (2, 11, and 12) out of a total of 36 possible outcomes (assuming a fair six-sided number cube). Therefore, the probability of X being a 2, 11, or 12 is 3/36, which can be simplified to 1/12.
Step-by-step explanation: