What is the distance to the earth's horizon from point P?
Enter your answer as a decimal in the box. Round only your final
answer to the nearest tenth.

Answers
Answer: 351.8
Step-by-step explanation:
Assuming a tangent is drawn, by the Pythagorean theorem,
\(x=\sqrt{(3959+15.6)^{2}-3959^{2}} \approx \boxed{351.8}\)
Related Questions
Combine the following expressions. a√ 125y-b √45y (-5a - 3b) (5a - 3b) (5a + 3b)
Answers
Combining the following expressions a√ 125y-b √45y will gives √5y(5a -3b)
How can the expressions be combined?given that a√125y-b √45y
a√125y = a5√5y
b √45y = b 3√5y
a5√5y - b 3√5y
Then we can now re arrange and collect like terms
√5y(5a -3b)
Therefore, if we combine the expresssion that was given from the question we can see that be will have √5y(5a -3b) which is the option Cbecause we can see that if we open the bracket by using the √5y to multiply the expression that is inside the bracket we will still have the given initial expression.
Learn more about expressions at:
https://brainly.com/question/1859113
#SPJ1

Billy went to the hardware store and bought 18 identical sections of pipe. The total length of the pipes was 45.18 meters. How
long was each pipe?

Answers
Answer:
2.51 meters
Step-by-step explanation:
The total length of the pipes was 45.18 meters
45.18/18 = 2.51 meter each identical section of pipe
Determine which line passing through the given points has a steeper slope.
Line 1:(0,-4) and (2,2)
Line 2:(0,-4) and (4,5)
Answers
The line which have a steeper slope is Line 1.
It is given in the question that the points on the line are given by:-
Line 1: (0,-4) and (2,2)
Line 2:(0,-4) and (4,5)
We have to find which line has a steeper slope.
First we will find the slope of each line.
We know that slope of a line with points (a,b) and (c,d) is given by:-
(d-b)/(c-a)
Slope of Line 1:
(2-(-4))/(2-0) = 6/2 = 3
Slope of Line 2:
(5-(-4))/(4-0) = 9/4 = 9/4 = 2.25
We know that greater the slope of the line means greater the steep of the line.
As,
3 > 2.25
Hence, Line 1 is steeper than Line 2.
To learn more about slope of a line, here:-
brainly.com/question/16180119
#SPJ4
Zeke and six of his friends are going to a baseball game. Their combined money totals $28.50. At the game, hot dogs cost $1.25 each, hamburgers cost $2.50 each, and sodas cost $0.50 each. Each person buys one soda. They spend all $28.50 on food and soda. Determine how many different combinations, including those combinations containing zero, of hot dogs and hamburgers Zeke and his friends can buy, spending all $28.50. ENTER
Answers
1.25x + 2.5y + 0.5z ≤ 28.5
is your inequality
Citrix Apps Apps CANVAS > Home EPB Intranet 7. -/2 points RogaCalcET4 13.5.017.Tutorial. Find r(t) and v(t) given a(t) and the initial velocity and position. a(t) = tk, v(0) = 4i, r(0) = 2; v(t) = r(t) = Additional Materials Tutorial +-12 points RogaCalcETA 19 rann
Answers
The position value, r(t) is equals to the (t³/6)k + 2j and velocity value, v(t) is equals to ( t²/2 )k + 4i , for a(t) = tk, v(0) = 4i, r(0) = 2j.
Acceleration is defined as the rate of change of the velocity of an object with respect to time. Accelerations are vector quanty.
a = dv/dt
We have the following informations are available,
Initial velocity, v(0) = 4i
Initial position, r(0) = 2j
Acceleration at any time "t",
a(t) = tk
we have to determine the value of v(t) and r(t).
As we know, a(t) = dv(t)/dt = tk
integrating the above equation ,
v(t) = ∫tk dt = ( t²/2 )k + c
at t = 0 , v(0) = 0 + c = 4i ( since, v(0) = 4i
=> c = 4i
So, v(t) = ( t²/2 )k + 4i
Also, velocity is calculated by derivative of postion (r) with respect to time.
=> v(t) = dr(t) /dt
=> r(t) = ∫ v(t) dt
=> r(t) = ∫ ( t²/2 )k dt
integrating value of the right hand side,
r(t) = ( t³/2×3 )k +d
= (t³/6)k + d
At t = 0, r(0) = (0/6)k + d
=> r(0) = d = 2j
so, r(t) = (t³/6)k + 2j
Hence, the required position and velocity are
(t³/6)k + 2j and ( t²/2 )k + 4i.
To learn more about Accelation , refer:
https://brainly.com/question/10307723
#SPJ4
8-7x-6-8x=5
solve for x
Answers
Answer:
x =-1/5Step-by-step explanation:
\(8-7x-6-8x=5\\\\\mathrm{Group\:like\:terms}\\-7x-8x+8-6=5\\\\\mathrm{Add\:similar\:elements:}\:-7x-8x=-15x\\-15x+8-6=5\\\\\mathrm{Add/Subtract\:the\:numbers:}\:8-6=2\\-15x+2=5\\\\\mathrm{Subtract\:}2\mathrm{\:from\:both\:sides}\\-15x+2-2=5-2\\\\Simplify\\-15x=3\\\\\mathrm{Divide\:both\:sides\:by\:}-15\\\frac{-15x}{-15}=\frac{3}{-15}\\\\Simplify\\x=-\frac{1}{5}\)
Find The Value of X.

Answers
Answer:
Step-by-step explanation:
The 2 angles with x in them are complementary. They add to 90. This is a right triangle.
3x - 14 + 2(3x - 6) = 90 Remove the brackets.
3x - 14 + 6x - 12 = 90 Combine
9x - 26 = 90 Add 26 to both sides.
9x = 116 Divide by 9
9x/9 = 116/9
x = 12.89
Chin was shown the graph of a line that contained point (1, 7). He wrote f(x) = 4x + 3 to correctly represent the line. Which of these equations could represent the same line?
y – 7 = 3(x – 1)
y – 1 = 3(x – 7)
y – 7 = 4(x – 1)
y – 1 = 4(x – 7)
Answers
Answer: it’s the third option
Step-by-step explanation:
Answer:
y – 7 = 4(x – 1)
Step-by-step explanation:
Third option
a(n) ? is a device that indicates whether two ac sources to be connected in parallel are in the correct phase relationship.
Answers
The device that indicates whether two AC sources to be connected in parallel are in the correct phase relationship is called a synchronizing device.
A synchronizing device is a mechanism that ensures that two AC sources are in sync when they are connected in parallel. It's used to match the voltage, frequency, and phase angle of two alternating current (AC) sources.
It guarantees that the power supplied by both generators is synchronized, allowing them to be combined into a single electrical system without disrupting the balance of the current or causing a short circuit.
As a result, it is critical to the safe and efficient operation of power systems. A phase sequence indicator (PSI) or a synchroscope is often used as a synchronizing device. It works by providing an indication of the voltage difference, the phase angle difference, and the frequency difference between two AC sources that are to be synchronized.
Therefore, a synchronizing device is an instrument that determines whether two alternating current (AC) sources to be connected in parallel are in the appropriate phase relationship.
To know more about synchronizing device click here:
https://brainly.com/question/4223074
#SPJ11
PLEASE HELP ASAP!!!! SUPER URGENT

Answers
Answer:
y = 2(x + 3)(x + 1)
Step-by-step explanation:
Use the formula y = a(x-b)(x-c)
b and c are the x-intercepts
The x-intercepts in this function are -3 and -1
y = a(x+3)(x+1)
substitute the point (-2, -1)
-2 = a(-2 + 3)(-2 + 1)
-2 = a(1)(-1)
-2 = -a
a = 2
y = 2(x + 3)(x + 1)
Which of the following is the most appropriate unit.to describe the rate at which a person reads
A) Minutes per word, because the independent quantity is in the minutes
B) Minutes per word, because the independent quantity is the words
C) Minutes per word, because the independent quantity is the minutes
D) Words per minute, because the independent quantity is the words
Answers
Evaluate the surface integral of the function g(x,y,z) over the surface s, where s is the surface of the rectangular prism formed from the coordinate planes and the planes x=2 y=2 z=3
Answers
The surface integral of the function g(x, y, z) over the surface S is evaluated.
To evaluate the surface integral, we consider the rectangular prism formed by the coordinate planes and the planes x = 2, y = 2, z = 3. This prism encloses a six-sided surface S. The surface integral of a function over a surface measures the flux or flow of the function across the surface.
In this case, we are integrating the function g(x, y, z) over the surface S. The specific form of the function g(x, y, z) is not provided in the given question. To evaluate the surface integral, we need to know the expression of g(x, y, z).
Once we have the expression for g(x, y, z), we can set up the integral by parameterizing the surface S and calculating the dot product of the function g(x, y, z) and the surface normal vector. The integral will involve integrating over the appropriate range of the parameters that define the surface.
Without the specific expression for g(x, y, z) or further details, it is not possible to provide the exact numerical evaluation of the surface integral. However, the general procedure for evaluating a surface integral involves parameterizing the surface, setting up the integral, and then performing the necessary calculations.
Learn more about Surface
brainly.com/question/32235761
brainly.com/question/1569007
#SPJ11
Explain how to change 36/60 into a decimal. Then turn it into a decimal.
Answers
Answer:
you divide 36/60 the decimal form is 0.6
Please help I will give brainliest

Answers
explanation in mistake done:
it is supposed to be like this : -27x - 5x = -32x in the 3rd line
other than that everything's ok
step by step:
= -27x - 5x = -32x
= -27x+26-5x
= -27x-5x+26
= -32x+26
btw, ur final answer is r8 tho
Find an explicit rule for the nth term of the arithmetic sequence. -20, -14, -8, -2, ... A. an = -20 + 6(n+2) B. an = -20 + 6(n-1) C. an = -20 Ã 6(n-1) D. an = -20 + 6(n+1)
Answers
the explicit rule of the nth term of the arithmetic
sequence is A. aₙ = 6n-8
B. aₙ = 6n-26
C. aₙ= 6n-26
D. aₙ =6n-14
What is arithmetic sequence?the sequence of numbers having constant differences between two successive numbers.
why explicit formula for arithmetic sequence is used?the explicit formula is used for determining any term of an arithmetic sequences directly in where only the first term and differences between two consecutive terms are needed to know.
Given, -20,-14,-8,-2,...are the terms. an explicit rule for the nth term of the arithmetic sequence is given by the formula, aₙ=a₁+(n-1) d
where, a₁ is the first term, aₙ is the nth term, d is the difference between two terms, n is the number of terms.
as per question a₁= -20, d= 6
now A. aₙ = -20+6(n+2)
aₙ = 6n-8
B. aₙ= -20+6(n-1)
aₙ = 6n-26
C. aₙ =-20+6(n-1)
aₙ = 6n-26
D. aₙ= -20+6(n+1)
aₙ = 6n-14
the above are the explicit rules for the arithmetic sequence.
to learn more about arithmetic sequence visit the link:
https://brainly.com/question/29755089
#SPJ4
is -(-3/2) equivalent to -3/2
Answers
Answer:
no it's equal to 3/2 because 2 negatives equal a positive number
hope this helps
have a good day :)
Step-by-step explanation:
Answer:
No, it's not equivalent
Step-by-step explanation:
\(-(\frac{3}{2} ) = 1\frac{1}{2\\}\)
\(-\frac{3}{2} = -1\frac{1}{2}\)
o. How much money is 8% of $15.00?
Answers
Answer: 1.2
Step-by-step explanation:
To get 8% you have to do 8/100
that equals .08
Multiply .08 with 15 and it equals 1.2
Answer1.2:
Step-by-step explanation:
find the missing number 9:4::63: ?
Answers
Answer: 28
Step-by-step explanation:
28 is thhe missing number
A cylindrical tank has a height of 11 feet and a diameter of 14 feet. Tallulah fills the tanks with water at a rate of 12 cubic feet per minute. At this rate, how many minutes will it take Tallulah to completely fill the tank without it overflowing?
Answers
It will take Tallulah approximately 141.17 minutes, or about 2 hours and 22 minutes, to completely fill the tank without it overflowing.
Volume of the cylinder:The volume of a cylinder can be calculated using the formula V = πr²h, where V is the volume, r is the radius, and h is the height.
By dividing the volume of the tank by the rate of filling, we can find the time it takes to completely fill the tank.
Here we have
A cylindrical tank has a height of 11 feet and a diameter of 14 feet.
Hence, Radius of tank = 14/2 = 7 feet
Tallulah fills the tanks with water at a rate of 12 cubic feet per minute.
Using the volume formula, V = πr²h
V = π(7²)(11) = 1694 cubic feet
Tallulah fills the tank at a rate of 12 cubic feet per minute.
=> 1694 / 12 = 141.17 minutes
Therefore,
It will take Tallulah approximately 141.17 minutes, or about 2 hours and 22 minutes, to completely fill the tank without it overflowing.
Learn more about Cylinder at
https://brainly.com/question/15621744
#SPJ1
One serving of a certain brand of microwave popcorn provides 150 calories, 90 of which are from fat. One serving of a certain brand of low-sodium pretzels provides 120 calories, 12 of which are from fat. How many more calories from fat are provided by a 100 calorie serving of the microwave popcorn than are provided by a 100-calorie serving of the pretzels?
Answers
Answer: 50 calories
Step-by-step explanation:
One serving of a certain brand of microwave popcorn provides 150 calories, 90 of which are from fat. The fraction that comes from fat:
= 90/150 = 3/5
One serving of a certain brand of low-sodium pretzels provides 120 calories, 12 of which are from fat. The fraction that comes from fat here:
= 12/120 = 1/10
The fat that are provided by a 100 calorie serving of the microwave popcorn would be:
= 3/5 × 100
= 60
The fat that are provided by a 100-calorie serving of the pretzels would be:
= 1/10 × 100 = 10
The difference from fat that are provided by a 100 calorie serving of the microwave popcorn than are provided by a 100-calorie serving of the pretzels would be:
= 60 - 10
= 50 calories
2. Write ONE algebraic rule that represents triangle JKL being translated to triangle J"K"L".
Answers
The original coordinates of JKL:
J(-3, -3), K(-4, 2) and L(2,1)
First, it is translated by the algebraic rule (x,y)->(x+2, y-3):
J(-3, -3)-> J'(-3+2, -3-3)=J'(-1, -6)
K(-4, 2) -> K'(-4+2, 2-3)= K'(-2, -1)
L(2,1) -> L'(2+2, 1-3)= L'(4, -2)
Then, this image is translated by (x,y)-> (x-2, y-1)
J'(-1, -6) -> J''(-1-2, -6-1) = J''(-3, -7)
K'(-2, -1) -> K''(-2-2, -1-1)= K''(-4, -2)
L'(4, -2) -> L''(4-2, -2-1)= L''( 2, -3)
Coordinates for triangle J''K''L'':
J''(-3, -7), K''(-4, -2) and L''( 2, -3)
2. To find algebraic rule that represents JKL to J''K''L'':
\(\begin{gathered} J^{\doubleprime}(-3,-7)\text{ and J(-3, -3)} \\ (x,y)\rightarrow(x,\text{ y+4)} \end{gathered}\)a racing car consumes a mean of 101 gallons of gas per race with a variance of 49 . if 43 racing cars are randomly selected, what is the probability that the sample mean would differ from the population mean by greater than 2.4 gallons? round your answer to four decimal places.
Answers
The probability that the sample mean would differ from the population mean by greater than 2.4 gallons
To solve this problem, we need to use the central limit theorem and the formula for the standard error of the mean:
Standard error of the mean = standard deviation / square root of sample size
In this case, the standard deviation is the square root of the variance, which is 7. Therefore, the standard error of the mean is:
Standard error of the mean = 7 / square root of 43 ≈ 1.061
Next, we need to calculate the z-score for a difference of 2.4 gallons:
z-score = (sample mean - population mean) / standard error of the mean
z-score = (101 - 101.6) / 1.061 ≈ -0.566
Note that we subtract the population mean from the sample mean because we want to know how much the sample mean differs from the population mean.
Finally, we can use a standard normal distribution table (or a calculator) to find the probability that a z-score is less than -0.566 or greater than 0.566 (since the distribution is symmetric). The probability of a z-sitcore less than -0.566 is approximately 0.2881, so the probability of a z-score greater than 0.566 is also approximately 0.2881. Therefore, the probability that the sample mean would differ from the population mean by greater than 2.4 gallons is:
Probability = 0.2881 + 0.2881 ≈ 0.5762
Rounding to four decimal places, the answer is 0.5762.
to learn more about probability click here -
https://brainly.com/question/13604758
#SPJ11
A airplane flies 3 hours. The distance is 1200 miles. What is the speed?
Answers
Answer:
400 mph
Step-by-step explanation:
1200/3 = 400 miles per hour
For the linear regression y = ẞ1 + ẞ2x + e, assuming that the sum of squared errors (SSE) takes the following form:
SSE = 382 +681 +382 + 18ẞ1ẞ2
Derive the partial derivatives of SSE with respect to B1 and B2 and solve the optimal values of these parameters.
a. B₁ = B1
b. B₂ =
Answers
The optimal values of these parameters are:
a. β₁ = 0
b. β₂ = 0
The linear regression y = β1 + β2x + e, assuming that the sum of squared errors (SSE) takes the following form:
SSE = 382 + 681 + 382 + 18β1β2
Derive the partial derivatives of SSE with respect to β1 and β2 and solve the optimal values of these parameters.
Given that SSE = 382 + 681 + 382 + 18β1β2 ∂SSE/∂β1 = 0 ∂SSE/∂β2 = 0
Now, we need to find the partial derivative of SSE with respect to β1.
∂SSE/∂β1 = 0 + 0 + 0 + 18β2 ⇒ 18β2 = 0 ⇒ β2 = 0
Therefore, we obtain the optimal value of β2 as 0.
Now, we need to find the partial derivative of SSE with respect to β2. ∂SSE/∂β2 = 0 + 0 + 0 + 18β1 ⇒ 18β1 = 0 ⇒ β1 = 0
Therefore, we obtain the optimal value of β1 as 0. Hence, the partial derivative of SSE with respect to β1 is 18β2 and the partial derivative of SSE with respect to β2 is 18β1.
Thus, the optimal values of β1 and β2 are 0 and 0, respectively.
Therefore, the answers are: a. β₁ = 0 b. β₂ = 0
Learn more about regression analysis at
https://brainly.com/question/31691955
#SPJ11
The following are the amounts of time, in minutes, that it took a random sample of 20 technicians to perform a certain task: 18.1, 20.3, 18.3, 15.6, 22.5, 16.8, 17.6, 16.9, 18.2, 17.0, 19.3, 16.5, 19.5, 18.6, 20.0, 18.8, 19.1, 17.5, 18.5, and 18.0. Assuming that this sample came from a symmetrical continuous population, use the sign test at the 0.05 level of significance to test the null hypothesis that the mean of this population is 19.4 minutes against the alternative hypothesis that it is not 19.4 minutes. Perform the test using(a) Table I;(b) the normal approximation to the binomial distribution.Rework Exercise 16.16 using the signed-rank test based on Table X.
Answers
Since the test statistic (-2.24) falls outside the range of the critical values (-1.96 to 1.96), we reject the null hypothesis.
What is sign test?
The sign test is a non-parametric statistical test used to determine whether the median of a distribution is equal to a specified value. It is a simple and robust method that is applicable when the data do not meet the assumptions of parametric tests, such as when the data
The given problem can be solved using the one-sample sign test to test the null hypothesis that the mean of the population is 19.4 minutes against the alternative hypothesis that it is not 19.4 minutes.
(a) Using Table I:
Step 1: Set up the hypotheses:
Null hypothesis (H0): The mean of the population is 19.4 minutes.
Alternative hypothesis (H1): The mean of the population is not 19.4 minutes.
Step 2: Determine the test statistic:
We will use the sign test statistic, which is the number of positive or negative signs in the sample.
Step 3: Set the significance level:
The significance level is given as 0.05.
Step 4: Perform the sign test:
Count the number of observations in the sample that are greater than 19.4 and the number of observations that are less than 19.4. Let's denote the count of observations greater than 19.4 as "+" and the count of observations less than 19.4 as "-".
In the given sample, there are 5 observations greater than 19.4 (18.1, 20.3, 19.3, 19.5, and 20.0), and 15 observations less than 19.4 (18.3, 15.6, 16.8, 17.6, 16.9, 17.0, 16.5, 18.6, 18.8, 19.1, 17.5, 18.5, and 18.0).
Step 5: Calculate the test statistic:
The test statistic is the smaller of the counts "+" or "-". In this case, the test statistic is 5.
Step 6: Determine the critical value:
Using Table I, for a significance level of 0.05 and a two-tailed test, the critical value is 3.
Step 7: Make a decision:
Since the test statistic (5) is greater than the critical value (3), we reject the null hypothesis.
(b) Using the normal approximation to the binomial distribution:
Alternatively, we can use the normal approximation to the binomial distribution when the sample size is large. Since the sample size is 20 in this case, we can apply this approximation.
Step 1: Set up the hypotheses (same as in (a)).
Step 2: Determine the test statistic:
We will use the z-test statistic, which is calculated as (x - μ) / (σ / √n), where x is the observed number of successes, μ is the hypothesized value (19.4), σ is the standard deviation of the binomial distribution (calculated as √(n/4), where n is the sample size), and √n is the standard error.
Step 3: Set the significance level (same as in (a)).
Step 4: Calculate the test statistic:
Using the formula for the z-test statistic, we get z = (5 - 10) / (√(20/4)) ≈ -2.24.
Step 5: Determine the critical value:
For a significance level of 0.05 and a two-tailed test, the critical value is approximately ±1.96.
Step 6: Make a decision:
Since the test statistic (-2.24) falls outside the range of the critical values (-1.96 to 1.96), we reject the null hypothesis.
Rework Exercise 16.16 using the signed-rank test based on Table X:
To provide a more accurate solution, I would need additional information about Exercise 16.16 and Table X.
To know more about sign test visit:
https://brainly.com/question/31486709
#SPJ4
the height of a cone is 16 cm and its base radius is 12 cm. find the curved surface area and the total surface area of the cone
Answers
Answer:
A≈1206.37 cm²
Step-by-step explanation:
Radius = 12
Height = 16
Using the formulas
A= πrl+πr²
l = √r²+h²
A=πr(r + √h²+r²)=
π·12·(12+√16²+12²) ≈1206.37158cm²

Given :
The height of a cone is 16 cm.Its base radius is 12 cm.⠀
To Find :
The curved surface area of the cone. The total surface area of the cone.⠀
Solution :
h = 16 cmr = 12 cmHere,
h is denoted as height. r is denoted as radius.So, from l² = h² + r², we have :
⠀
The slang height of the cone is represented by l.⠀
\({\qquad \sf \dashrightarrow{ \: l = \sqrt{ {h}^{2} + {r}^{2} \: }cm }}\)
\({\qquad \sf \dashrightarrow{ \: l = \sqrt{ {(16)}^{2} + {(12)}^{2} \: }cm }}\)
\({\qquad \sf \dashrightarrow{ \: l = \sqrt{ 256 + 144 } \: cm }}\)
\({\qquad \sf \dashrightarrow{ \: l = \sqrt{ 400} \: cm }}\)
\({\qquad \sf \dashrightarrow{ \: \bf l = 20 \: cm }}\)
⠀
So, Curved surface area = \( \pi{rl}\)
\({\qquad \sf \dashrightarrow \: 3.14 \times 12 \times 20 \: {cm}^{2} }
\)
\({\qquad \bf \dashrightarrow \: 753.6 \: {cm}^{2} }
\)
⠀
Further, total surface area = \( \pi{rl} + \pi{ {r}^{2} }\)
\({\qquad \sf \dashrightarrow \: (753.6 + 3.14 \times 12 \times 12 )\: {cm}^{2} }\)
\({\qquad \sf \dashrightarrow \: (753.6 + 452.16 )\: {cm}^{2} }\)
\({\qquad \bf \dashrightarrow \: 1205.76 \: {cm}^{2} }\)
$n$ is a four-digit positive integer. dividing $n$ by $9$, the remainder is $5$. dividing $n$ by $7$, the remainder is $3$. dividing $n$ by $5$, the remainder is $1$. what is the smallest possible value of $n$?
Answers
To find the smallest possible value of $n$, we need to find the smallest value that satisfies all three conditions.
From the first condition, we know that $n = 9a + 5$ for some positive integer $a$.
From the second condition, we know that $n = 7b + 3$ for some positive integer $b$.
From the third condition, we know that $n = 5c + 1$ for some positive integer $c$.
We can set these equations equal to each other and solve for $n$:
$9a + 5 = 7b + 3 = 5c + 1$
Starting with the first two expressions:
$9a + 5 = 7b + 3 \Rightarrow 9a + 2 = 7b$
The smallest values of $a$ and $b$ that satisfy this equation are $a=2$ and $b=3$, which gives us $n = 9(2) + 5 = 7(3) + 3 = 23$.
Now we need to check if this value of $n$ satisfies the third condition:
$n = 23 \not= 5c + 1$ for any positive integer $c$.
So we need to try the next possible value of $a$ and $b$:
$9a + 5 = 5c + 1 \Righteous 9a = 5c - 4$
$7b + 3 = 5c + 1 \Righteous 7b = 5c - 2$
If we add 9 times the second equation to 7 times the first equation, we get:
$63b + 27 + 49a + 35 = 63b + 45c - 36 + 35b - 14$
Simplifying:
$49a + 98b = 45c - 23$
$7a + 14b = 5c - 3$
$7(a + 2b) = 5(c - 1)$
So the smallest possible value of $c$ is 2, which gives us $a + 2b = 2$. The smallest values of $a$ and $b$ that satisfy this equation are $a=1$ and $b=1$, which gives us $n = 9(1) + 5 = 7(1) + 3 = 5(2) + 1 = 46$.
Therefore, the smallest possible value of $n$ is $\boxed{46}$.
To find the smallest possible value of $n$ which is a four-digit positive integer such that dividing $n$ by $9$, the remainder is $5$, dividing $n$ by $7$, the remainder is $3$, and dividing $n$ by $5$, the remainder is $1$, follow these steps:
Step 1: Write down the congruences based on the given information.
$n \equiv 5 \pmod{9}$
$n \equiv 3 \pmod{7}$
$n \equiv 1 \pmod{5}$
Step 2: Use the Chinese Remainder Theorem (CRT) to solve the system of congruences. The CRT states that for pairwise coprime moduli, there exists a unique solution modulo their product.
Step 3: Compute the product of the moduli.
$M = 9 \times 7 \times 5 = 315$
Step 4: Compute the partial products.
$M_1 = M/9 = 35$
$M_2 = M/7 = 45$
$M_3 = M/5 = 63$
Step 5: Find the modular inverses.
$M_1^{-1} \equiv 35^{-1} \pmod{9} \equiv 2 \pmod{9}$
$M_2^{-1} \equiv 45^{-1} \pmod{7} \equiv 4 \pmod{7}$
$M_3^{-1} \equiv 63^{-1} \pmod{5} \equiv 3 \pmod{5}$
Step 6: Compute the solution.
$n = (5 \times 35 \times 2) + (3 \times 45 \times 4) + (1 \times 63 \times 3) = 350 + 540 + 189 = 1079$
Step 7: Check that the solution is a four-digit positive integer. Since 1079 is a three-digit number, add the product of the moduli (315) to the solution to obtain the smallest four-digit positive integer that satisfies the conditions.
$n = 1079 + 315 = 1394$
The smallest possible value of $n$ is 1394.
Visit here to learn more about Chinese Remainder Theorem:
brainly.com/question/30806123
#SPJ11
Solve -2/3x>8 or -2/3x<4
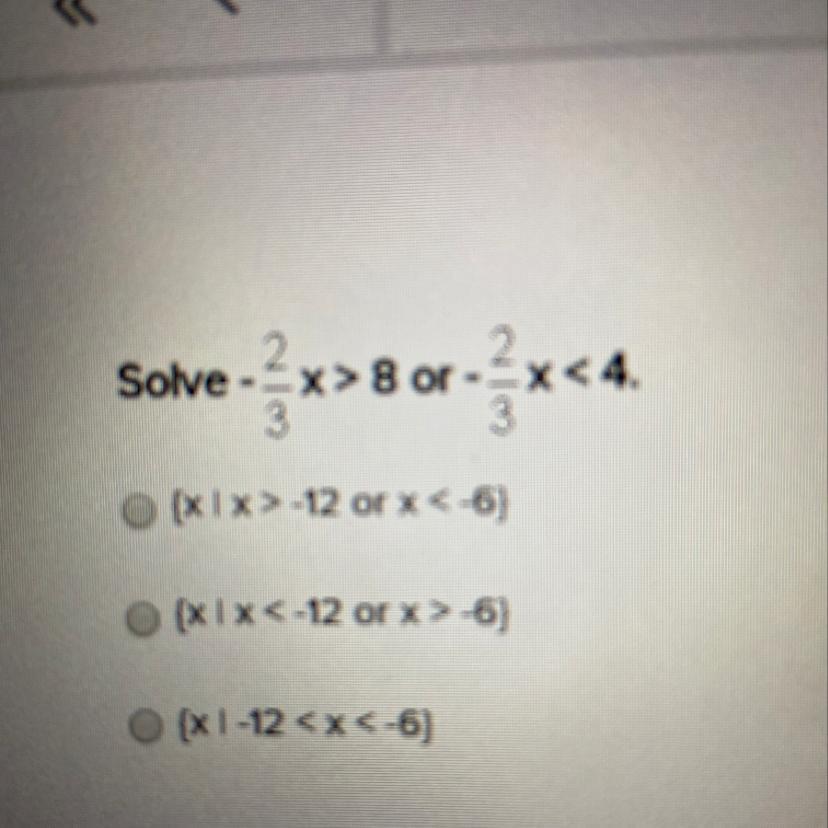
Answers
Answer:
u = -32
Step-by-step expla
Simplify
Answer:
(x | x< -12 or x> -6)
Step-by-step explanation:
-2/3x>8 ⇒ -2/3x*3/2>8*3/2 ⇒ -x> 12 ⇒ x< -12
-2/3x<4 ⇒ -2/3x*3/2<4*3/2 ⇒ -x< 6 ⇒ x> -6
(x | x< -12 or x> -6)
15 points :) ill mark BRAINIEST

Answers
Answer:
7 = 7x - 48
Step-by-step explanation:
Use point slope formula: y - y1 = m(x - x1)
Find slope:
(8 -(-6)) / (8 - 6)
14/2
m = 7/1
Subsitute x1 and y1, solve for y.
y - 8 = 7(x - 8)
y - 8 = 7x - 56
y = 7x - 48
in the morning, the train went 170 miles. in the afternoon the train went 50 more miles. how far did the train end up going?
Answers
In the morning, the train went 170 miles. in the afternoon the train went 50 more miles. The Train ended up going 220 miles in total.
In the morning, the train traveled 170 miles.
In the afternoon, it traveled an additional 50 miles.
To find the total distance traveled by the train, we need to add the distance traveled in the morning and the distance traveled in the afternoon:
Total distance = Distance traveled in the morning + Distance traveled in the afternoon
Total distance = 170 miles + 50 miles
Total distance = 220 miles
So, the train ended up traveling a total of 220 miles.
To learn more about trains click on,
https://brainly.com/question/29326122
#SPJ4