What interest is needed to earn $137.50 on a deposit of $500 for five years if it earns simple interest?
Answers
Answer:
5.5%
Step-by-step explanation:
Given data
Simple interest = $137.50
Principal= $500
time = 5 years
We want to find the rate R
Simple interest= PRT/100
137.50 = 500*R*5/100
137.50=2500R/100
cross multiply
137.5*100= 2500R
13750= 2500R
divide both sides by 2500
R= 13750/2500
R=5.5%
Hence the rate is 5.5%
Related Questions
HURRY ANSWER Determine whether the graph shows a positive correlation, a negative correlation, or no correlation. If there is a positive on
negative correlation, describe its meaning in the situation.
Consumer Price Index, 1950-2002
700
600+
500
400
300
200+
100
1950
1960
1970
1980
1990
2000
Year
Source: Bureau of Labor Statistics, U.S. Dept. of Labor
a. no correlation
b. positive correlation; as time passes, the CPI increases.
C.positive correlation as time passes
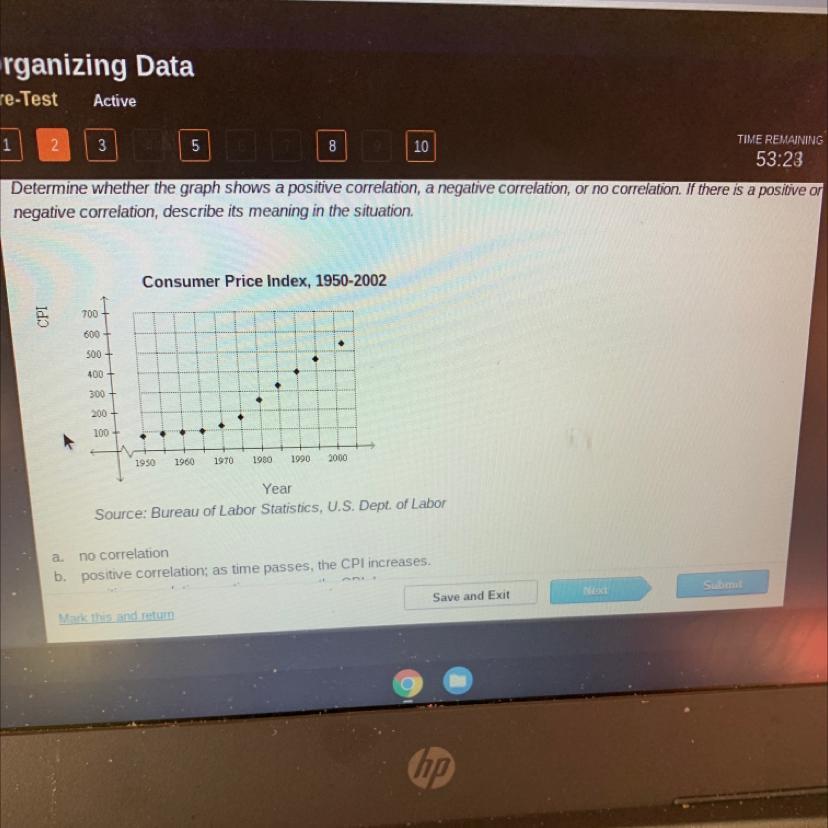
Answers
Answer:
B
Step-by-step explanation:
The meaning in the situation is B; positive correlation; as time passes, the CPI increases.
What does correlation coefficient convey?The correlation coefficient is the degree of association between two quantities in terms of linear relation. The range of correlation coefficient is -1 to 1
If the correlation is -1, then that refers as the one quantity increases, the other quantity decreases , also the correlation is 0, then there is no linear relationship between two variables.
There are two types of Correlation;
Positive Correlation= With Increase in x value, y value also increases, we call it positive correlation.
Negative Correlation= With Increase in x value, if y value decreases, we call it negative correlation.
As we can see from the points plotted on the graph ,with increase in x value , y value decreases.
Hence, positive correlation; as time passes, the CPI increases.
Learn more about correlation coefficient here:
https://brainly.com/question/10725272
#SPJ3
please help asap!!!!!!!!!!!!!!!!!!!!!

Answers
Answer:
X=29
Step-by-step explanation:
Sin62=x/33
X=29.137≈29
In a lottery, the top cash prize was $642 million, going to three lucky winners. Players pick five different numbers from 1 to 56 and one number from 1 to 49.
Save
A player wins a minimum award of $225 by correctly matching three numbers drawn from the white balls (1 through 56) and matching the number on the gold ball (1 through 49). What is the probability of winning the minimum award?
The probability of winning the minimum award is
Answers
Total number of possible outcomes:
Number of ways to choose 3 numbers from 56 (56 choose 3): 56! / (3! * (56 - 3)!) = 22,957
Number of ways to choose 1 number from 49: 49
Total number of possible outcomes = 22,957 * 49 = 1,128,593
Number of favorable outcomes:
Number of ways to choose 1 number from 49: 1
Number of favorable outcomes = 1
Probability of winning the minimum award:
Probability = Number of favorable outcomes / Total number of possible outcomes
Probability = 1 / 1,128,593 ≈ 0.000000888, or approximately 0.0000888%
What is the net force for this free body diagram below?

Answers
20.
What should be added to 2/3+3/5 to get-2/15
Answers
Answer:
no it gate 19/15 or 1 4/15
Step-by-step explanation:
Michelle is also a contestant. On day 21, she is informed by the wellness team that she has lost 17% of her body weight. Michelle weighed 145 lb. at the start of the competition. How much does she weigh now?
Answers
Answer:
Michelle weighs 120.15 lb. now.
You can calculate it by
145lb x (1-.17) = 145lb x .83 = 120.15lb
this month the middle school media newspaper has 25 pages. Twenty-five schools order the paper for each of their students. Each of the students has 25 classrooms with 25 students in each classroom. What expression with an exponent shows the total number of pages in all of the newspapers?
Answers
Answer:
56
Step-by-step explanation:
7 times 8=56
Below are monthly rents paid by 30 students who live off campus.
640 640 640 840 610 500
600 940 650 530 630 595
470 650 560 570 760 830
510 530 670 600 620 410
640 710 730 750 630 655
Answers
1. We want to know how much money Houston people would like to spend on
restaurants every month. So we randomly find 500 volunteers to do a survey
questionnaire. Identify the population.
A. 500 volunteers
B. Houston people
Answers
Part A: Elijah has 1/2 bag of candy. A bag of candy weighs 5 pounds. How many pounds of candy does Elijah have?
Part B: Elijah has 2 1/2 bags of candy. A bag of candy weighs 5 pounds. How many pounds of candy does Elijah have?
Answers
Answer:
A. 2.5 pounds
B. 12.5 pounds
Step-by-step explanation:
Answer:
a 2.5 b 12.5
Step-by-step explanation:
The maximum height of a vehicle that can safely pass under a bridge is 12 feet 5 inches. A truck measures 162 inches in height. Which best explains whether or not the truck can pass safely under the bridge?
Answers
162 inches is 13.5 feet or 13 feet 6 inches, so it would not fit underneath the bridge
Answer:
The truck cannot pass safely under the bridge. The truck is 13 inches taller than the maximum height.
all the cubes root of
\( \sqrt{3 + i} \)
Answers
If you're looking for the cube roots of √(3 + i ), you first have to decide what you mean by the square root √(…), since 3 + i is complex and therefore √(3 + i ) is multi-valued. There are 2 choices, but I'll stick with 1 of them.
First write 3 + i in polar form:
3 + i = √(3² + 1²) exp(i arctan(1/3)) = √10 exp(i arctan(1/3))
Then the 2 possible square roots are
• √(3 + i ) = ∜10 exp(i arctan(1/3)/2)
• √(3 + i ) = ∜10 exp(i (arctan(1/3)/2 + π))
and I'll take the one with the smaller argument,
√(3 + i ) = ∜10 exp(i arctan(1/3)/2)
Then the 3 cube roots of √(3 + i ) are
• ∛(√(3 + i )) = ¹²√10 exp(i arctan(1/3)/6)
• ∛(√(3 + i )) = ¹²√10 exp(i (arctan(1/3)/6 + π/3))
• ∛(√(3 + i )) = ¹²√10 exp(i (arctan(1/3)/6 + 2π/3))
On the off-chance you meant to ask about the cube roots of 3 + i, and not √(3 + i ), then these would be
• ∛(3 + i ) = ⁶√10 exp(i arctan(1/3)/3)
• ∛(3 + i ) = ⁶√10 exp(i (arctan(1/3)/3 + 2π/3))
• ∛(3 + i ) = ⁶√10 exp(i (arctan(1/3)/6 + 4π/3))
I just need brainliest please
Answers
Answer:
alright if you give me brianliest on this, when you answer one of my questions ill give you brainliest. brailiest for a brianliest?
Step-by-step explanation:
Answer
Catfishing, In LOl rate 0-10 Im bored
Step-by-step explanation:
The linear equations 4x - 2y = 7 and 3x + y = 4 intersect. find the coordinates of the point where the equations intersect.
Answers
Answer: (1.5,-0.5)
Step-by-step explanation:
Simplify the expression.
4+ 5(3x - 2) – 3x
Help plsss and no links plsss
Remember no links

Answers
Step-by-step explanation:
→ 4 + 5(3x - 2) - 3x
→ 4 + 15x - 10 - 3x
→ 12x - 6
therefore, option A is correct.
hope this answer helps you dear!
The required simplified solution of the given expression is 12x -6. Option A is correct.
What is simplification?The process in mathematics to operate and interpret the function to make the function or expression simple or more understandable is called simplifying and the process is called simplification.
Here,
= 4 + 5(3x -2) - 3x
Following the distributive property,
= 4 + 15x - 10 - 3x
Following the associative property,
= 4 - 10 + 15x - 3x
= -6 + 12x
= 12x - 6
Thus, the required simplified solution of the given expression is 12x -6. Option A is correct.
Learn more about simplification here:
https://brainly.com/question/12501526
#SPJ2
hi i will give 50 POINTS and BRAINLIEST to whoever answers this question

Answers
Answer:
\(x = - \frac{13}{3} \)Step-by-step explanation:
\(6x + 7 = 3x - 6\)
Move variable to L.H.S and change its sign
Similarly, Move constant to R.H.S and change its sign
\(6x - 3x = - 6 - 7\)
Collect like terms
\(3x = - 6 - 7\)
Calculate
\( 3x = - 13\)
Divide both sides of the equation by 3
\( \frac{3x}{3} = - \frac{13}{3} \)
Calculate
\(x = - \frac{13}{3} \)
Hope this helps...
Best regards!!
Answer:
x= -13/3
Step-by-step explanation:
To solve for x, we need to get x by itself.
6x+7= 3x-6
First, move all the terms with variables to the left side of the equation.
Subtract 3x from both sides of the equation.
6x-3x +7 = 3x-3x-6
(6x-3x)+7=-6
3x+7=6
Now, we must move all the constants (terms without variables) to the right side of the equation.
Subtract 7 from both sides of the equation.
3x+7-7=-6-7
3x= -6-7
3x= -13
Now all the variables are on side and the constants are on the other. x is not by itself yet, it is being multiplied by 3. The inverse of multiplication is division. Divide both sides by 3.
3x/3= -13/3
x= -13/3
This fraction cannot be simplified, therefore it is our final answer.
Coaching companies claim that their courses can raise the SAT scores of high school students. But students who retake the SAT without paying for coaching also usually raise their scores. A random sample of students who took the SAT twice found 427 who were coached and 2733 who were uncoached. Starting with their verbal scores on the first and second tries, we have these summary statistics: Try 1 Try 2 Gain n \overline x s \overline x s \overline x sCoached 427 500 92 529 97 29 59Uncoached 2733 506 101 527 101 21 52Use Table C to estimate a 90% confidence interval for the mean gain of all students who are coached.toat 90% confidence.Now test the hypothesis that the score gain for coached students is greater than the score gain for uncoached students. Let \mu_1 be the score gain for all coached students. Let \mu_2 be the score gain for uncoached students.(a) Give the alternative hypothesis: \mu_1 - \mu_20.(b) Give the t test statistic:(c) Give the appropriate critical value for \alpha =5%: .
Answers
Answer:
Step-by-step explanation:
The question is incomplete. The complete question is
Coaching companies claim that their courses can raise the SAT scores of high school students. But students who retake the SAT without paying for coaching also usually raise their scores. A random sample of students who took the SAT twice found 427 who were coached and 2733 who were uncoached. Starting with their verbal scores on the first and second tries, we have these summary statistics:
Try 1 Try 2 Gain
n x s x s x s
Coached 427 500 92 529 97 29 59
Uncoached 2733 506 101 527 101 21 52
Use Table C to estimate a 90% confidence interval for the mean gain of all students who are coached.
at 90% confidence.
Now test the hypothesis that the score gain for coached students is greater than the score gain for uncoached students. Let μ1 be the score gain for all coached students. Let μ2 be the score gain for uncoached students.
(a) Give the alternative hypothesis:
μ1 - μ2.
(b) Give the t test statistic:
(c) Give the appropriate critical value for \alpha =5%:
Solution:
The formula for determining the confidence interval for the difference of two population means is expressed as
Confidence interval = (x1 - x2) ± z√(s²/n1 + s2²/n2)
Where
x1 = sample mean score gain for all coached students
x2 = sample mean score gain for all uncoached students
s1 = sample standard deviation score gain of coached students
s2 = sample standard deviation score gain of uncoached students
For a 90% confidence interval, the z score is 1.645
From the information given,
x1 = 29
s1 = 59
n1 = 427
x2 = 21
s2 = 52
n2 = 2733
x1 - x2 = 29 - 21 = 8
z√(s1²/n1 + s2²/n2) = 1.645√(59²/427 + 52²/2733) = 4.97
90% Confidence interval = 8 ± 4.97
a) The population standard deviations are not known. it is a two-tailed test. The random variable is μ1 - μ2 = difference in the score gain for coached and uncoached students.
We would set up the hypothesis.
The null hypothesis is
H0 : μ1 = μ2 H0 : μ1 - μ2 = 0
The alternative hypothesis is
H1 : μ1 > μ2 H1 : μ1 - μ2 > 0
This is a right tailed test.
b) Since sample standard deviation is known, we would determine the test statistic by using the t test. The formula is
(x1 - x2)/√(s1²/n1 + s2²/n2)
t = (29 - 21)/√(59²/427 + 52²/2733)
t = 2.65
The formula for determining the degree of freedom is
df = [s1²/n1 + s2²/n2]²/(1/n1 - 1)(s1²/n1)² + (1/n2 - 1)(s2²/n2)²
df = [59²/427 + 52²/2733]²/[(1/427 - 1)(59²/427)² + (1/2733 - 1)(52²/2733)²] = 9.14/0.1564
df = 58
c) from the t distribution table, the critical value is 1.67
In order to reject the null hypothesis, the test statistic must be smaller than - 1.67 or greater than 1.67
Since - 2.65 < - 1.67 and 2.65 < 1.67, we would reject the null hypothesis.
Therefore, at 5% significance level, we can conclude that the score gain for coached students is greater than the score gain for uncoached students.
URGENT PLEASE HELP asap

Answers
Answer:
4x-4 < -76
Step-by-step explanation:
Four times a number (x), minus 4, is less than -76.
Answer:
x is less than —18
Step-by-step explanation:
Check out the attached photo

A bucket contains six white balls and five red balls. A sample of four balls is selected
at random from the bucket, without replacement. What is the probability that the
sample contains...
Exactly two white balls and two red balls?
At least two white balls?
Answers
To solve this problem, we can use the formula for probability:
P(event) = number of favorable outcomes / total number of outcomes
First, let's find the total number of outcomes. We are selecting 4 balls from 11 without replacement, so the total number of outcomes is:
11C4 = (11!)/(4!(11-4)!) = 330
where nCr is the number of combinations of n things taken r at a time.
Now let's find the number of favorable outcomes for each part of the problem.
Part 1: Exactly two white balls and two red balls
To find the number of favorable outcomes for this part, we need to select 2 white balls out of 6 and 2 red balls out of 5. The number of ways to do this is:
6C2 * 5C2 = (6!)/(2!(6-2)!) * (5!)/(2!(5-2)!) = 15 * 10 = 150
So the probability of selecting exactly two white balls and two red balls is:
P(2W2R) = 150/330 = 0.45 (rounded to two decimal places)
Part 2: At least two white balls
To find the number of favorable outcomes for this part, we need to consider two cases: selecting 2 white balls and 2 red balls, or selecting 3 white balls and 1 red ball.
The number of ways to select 2 white balls and 2 red balls is the same as the number of favorable outcomes for Part 1, which is 150.
To find the number of ways to select 3 white balls and 1 red ball, we need to select 3 white balls out of 6 and 1 red ball out of 5. The number of ways to do this is:
6C3 * 5C1 = (6!)/(3!(6-3)!) * (5!)/(1!(5-1)!) = 20 * 5 = 100
So the total number of favorable outcomes for selecting at least two white balls is:
150 + 100 = 250
And the probability of selecting at least two white balls is:
P(at least 2W) = 250/330 = 0.76 (rounded to two decimal places)
Find the volume, v of the largest right circular cone that can be inscribed in a sphere of radius, r=18 cm.
Answers
The volume of the largest right circular cone that can be inscribed in a sphere of radius 18 cm is approximately 11622.85 cubic centimeters.
To find the largest right circular cone that can be inscribed in a sphere of radius 18 cm, we need to find the cone with the largest possible volume that can fit inside the sphere.
Let's assume that the apex of the cone is at the center of the sphere. Since the cone is a right circular cone, the base of the cone will lie on the surface of the sphere, forming a circle with radius equal to the radius of the sphere, which is 18 cm.
Let's call the height of the cone "h" and the radius of the base of the cone "r". Then we can use the Pythagorean theorem to relate the height, radius, and slant height (which is equal to the radius of the sphere):
r^2 + h^2 = (18 cm)^2
The volume of a cone can be expressed as V = (1/3)πr^2h. We want to maximize this expression subject to the constraint above. We can use the constraint to eliminate one of the variables in the volume expression, then differentiate with respect to the remaining variable and set the derivative equal to zero to find the maximum.
From the constraint, we can solve for h^2:
h^2 = (18 cm)^2 - r^2
Substituting into the volume expression, we get:
V = (1/3)πr^2(18 cm - sqrt(r^2 + h^2))
Simplifying this expression, we get:
V = (1/3)πr^2(18 cm - sqrt((18 cm)^2 - r^2))
Differentiating with respect to r, we get:
dV/dr = (1/3)π(36 cm)r - (1/3)πr^3/sqrt((18 cm)^2 - r^2)
Setting this equal to zero and solving for r, we get:
r = (18 cm)/sqrt(2)
Substituting this value of r back into the expression for h, we get:
h = (18 cm)/sqrt(2)
Finally, substituting these values of r and h into the expression for the volume, we get:
V = (1/3)π((18 cm)/sqrt(2))^2((18 cm) - sqrt(((18 cm)/sqrt(2))^2 + ((18 cm)/sqrt(2))^2))
Simplifying this expression, we get:
V ≈ 11622.85 cubic centimeters
Learn more about volume here
brainly.com/question/30209128
#SPJ4
A physician orders a dosage of 85mg. The drug on hand is labeled “0.1g in 1.5mL”. How many ML should the pharmacy technician give the patient?
Answers
Answer:
Step-by-step explanation:
0.1 g = 100 mg
85 mg / 100 mg = x mL / 1.5 mL
x = 1.275 mL
3 6 9 12 15 18 21 24 27 30 is odd or even numbers?
Answers
Answer: Half of them are even and half of them are odd.
Step-by-step explanation:
The even numbers are 6, 12, 18, 24, and 30. An even number is defined as a number that is divisible by 2, meaning it has no remainder when divided by 2. For example, 6 divided by 2 equals 3 with no remainder, so 6 is even.
The odd numbers are 3, 9, 15, 21, and 27. An odd number is defined as a number that is not divisible by 2, meaning it has a remainder of 1 when divided by 2. For example, 9 divided by 2 equals 4 with a remainder of 1, so 9 is odd.
Therefore, out of the given numbers, half of them are even and half of them are odd.
________________________________________________________
Recorded here are the germination times (in days) for ten randomly chosen seeds of a new type of bean. See Attached Excel for Data. Assume that the population germination time is normally distributed. Find the 99% confidence interval for the mean germination time.
Answers
Answer:
The 99% confidence interval for the mean germination time is (12.3, 19.3).
Step-by-step explanation:
The question is incomplete:
Recorded here are the germination times (in days) for ten randomly chosen seeds of a new type of bean: 18, 12, 20, 17, 14, 15, 13, 11, 21, 17. Assume that the population germination time is normally distributed. Find the 99% confidence interval for the mean germination time.
We start calculating the sample mean M and standard deviation s:
\(M=\dfrac{1}{n}\sum_{i=1}^n\,x_i\\\\\\M=\dfrac{1}{10}(18+12+20+17+14+15+13+11+21+17)\\\\\\M=\dfrac{158}{10}\\\\\\M=15.8\\\\\\\)
\(s=\sqrt{\dfrac{1}{n-1}\sum_{i=1}^n\,(x_i-M)^2}\\\\\\s=\sqrt{\dfrac{1}{9}((18-15.8)^2+(12-15.8)^2+(20-15.8)^2+. . . +(17-15.8)^2)}\\\\\\s=\sqrt{\dfrac{101.6}{9}}\\\\\\s=\sqrt{11.3}=3.4\\\\\\\)
We have to calculate a 99% confidence interval for the mean.
The population standard deviation is not known, so we have to estimate it from the sample standard deviation and use a t-students distribution to calculate the critical value.
The sample mean is M=15.8.
The sample size is N=10.
When σ is not known, s divided by the square root of N is used as an estimate of σM:
\(s_M=\dfrac{s}{\sqrt{N}}=\dfrac{3.4}{\sqrt{10}}=\dfrac{3.4}{3.162}=1.075\)
The degrees of freedom for this sample size are:
df=n-1=10-1=9
The t-value for a 99% confidence interval and 9 degrees of freedom is t=3.25.
The margin of error (MOE) can be calculated as:
\(MOE=t\cdot s_M=3.25 \cdot 1.075=3.49\)
Then, the lower and upper bounds of the confidence interval are:
\(LL=M-t \cdot s_M = 15.8-3.49=12.3\\\\UL=M+t \cdot s_M = 15.8+3.49=19.3\)
The 99% confidence interval for the mean germination time is (12.3, 19.3).
A quiz consists of 20 multiple-choice questions, each with 4 possible answers. For someone who makes random guesses for all of the answers, find the probability of passing if the minimum passing grade is 70 %.
Answers
evaluate -4 - 5+4+(-5)
Answers
We open the bracket so it becomes -4-5+4-5
-4-1-5
=-10
The triangle above has the following measures.
s = 29 m
r= 63 m
Find the m/Q.
Round to the nearest tenth and include correct units.
Show all your work.


Answers
The value of m∠Q as shown in the right-angled triangle below is 62.59°.
The Formula used is:
m∠Q = cos⁻¹(s/r)........................ (1)
Where:
s = 29 m
r = 63 m
Now, Substitute these values into equation 1
m∠Q = cos⁻¹(29/63)
m∠Q = cos⁻¹(0.46)
m∠Q = 62.59°
Learn more about right-angle triangle here:
brainly.com/question/31203729
#SPJ1
What is the sum of the first 37 terms of the arithmetic sequence?
−27,−21,−15,−9,...
Enter your answer in the box.
Answers
Answer:
The sum of the first 37 terms of the arithmetic sequence is 2997.
Step-by-step explanation:
Arithmetic sequence concepts:
The general rule of an arithmetic sequence is the following:
\(a_{n+1} = a_{n} + d\)
In which d is the common diference between each term.
We can expand the general equation to find the nth term from the first, by the following equation:
\(a_{n} = a_{1} + (n-1)*d\)
The sum of the first n terms of an arithmetic sequence is given by:
\(S_{n} = \frac{n(a_{1} + a_{n})}{2}\)
In this question:
\(a_{1} = -27, d = -21 - (-27) = -15 - (-21) = ... = 6\)
We want the sum of the first 37 terms, so we have to find \(a_{37}\)
\(a_{n} = a_{1} + (n-1)*d\)
\(a_{37} = a_{1} + (36)*d\)
\(a_{37} = -27 + 36*6\)
\(a_{37} = 189\)
Then
\(S_{37} = \frac{37(-27 + 189)}{2} = 2997\)
The sum of the first 37 terms of the arithmetic sequence is 2997.
Peter set off from Town A at 10 am, driving at an average speed of 84 km/h. He reached
Town B at 2 pm. If William set off 1 hour 25 minutes earlier than Peter and took the
same route at an average speed of 70 km/h, at what time would William reach Town B?
Answers
Peter left Town A around 10 a.m., traveling at an average speed of 84 km/h. William would reach Town B at 1:23 PM.
Firstly, we need to find the distance between Town A and Town B which can be calculated by calculating the distance travelled by Peter
Time taken by Peter = 2PM - 10AM
= 4 hrs
Speed of Peter = 84 km/h
Distance travelled by Peter = speed × time
= 84 × 4
= 336 km
So, the distance between Town A and Town B = distance travelled by Peter = 336 km.
Now, we will calculate time taken by William.
Speed of William = 70 km / hr
Distance travelled by William = distance between Town A and town B = 336 km
Time taken by William = distance / speed
= 336 / 70 hr
= 4.8 hr
This can b converted into hrs and minutes
4.8 hr = 4 hr + 0.8 × 60
= 4 hr 48 mins
Time William took off = 10 AM - 1hr 25 mins
= 8:35 AM
Now, we will calculate the time William would reach town B.
Time = 8:35 + 4hr 48 mins
= 1:23 PM
To know more about speed:
https://brainly.com/question/31756299
#SPJ1
how do i work out 320.041 - 47.96
Answers
To subtract 47.96 from 320.041, you can align the decimal points and then subtract each digit from right to left.
First, write the numbers with the decimal points aligned:
320.041
- 47.960
Next, subtract the digits in the ones place, which is 1 minus 0, resulting in 1. Then, subtract the digits in the tenths place, which is 4 minus 6. Since 4 is less than 6, you need to borrow 1 from the digit to the left, making the 2 into a 1 and adding 10 to the 4, giving you 14. So, 14 minus 6 equals 8.
Continue subtracting each digit in the same way:
320.041
- 47.960
= 272.081
Therefore, 320.041 minus 47.96 is equal to 272.081.
To learn more about subtraction click on,
https://brainly.com/question/2346316
#SPJ1
Solve the equation below for x.
1/2(x+2)=7/5
Answers
Answer:
x = 4/5
Step-by-step explanation: