\((5 \sqrt{3} ) {}^{2} + 5 { }^{2} = x {}^{2} \)
Answers
is that what you’re looking for ?
Related Questions
when performing a hypothesis test on μ when σ is known, h0 can never be rejected if
Answers
When performing a hypothesis test on the population mean (μ) when the population standard deviation (σ) is known, the null hypothesis (H0) can never be rejected if the sample mean falls within the acceptance range determined by the chosen significance level and the critical values.
In hypothesis testing for the population mean when the population standard deviation is known, the null hypothesis (H0) represents the claim or assumption that the population mean is equal to a specific value. The alternative hypothesis (Ha) states that the population mean is not equal to the specific value.
To determine whether to reject or fail to reject the null hypothesis, we compare the sample mean to the expected value under the null hypothesis. If the sample mean falls within the acceptance range determined by the chosen significance level and the critical values, we do not have sufficient evidence to reject the null hypothesis. The acceptance range is defined by the margin of error around the expected value, and it indicates the range of values that can be considered reasonably close to the expected value.
To know more about hypothesis test,
https://brainly.com/question/29540386
#SPJ11
The table shows the speeds of the four fastest drivers in a car race.
Driver
Speed (miles per hour)
Marco
224.362
Finn
224.136
Will
224.48
Liz
224.392
Did Marco win this week's race? Use words and numbers to justify your answer.
Answer:
14
Answers
Marco only got 2nd place
Step-by-step explanation:
Which of the following is equivalent to 2x - 5y = 10?

Answers
y = 2x/5 - 2 (option B)
Explanation:We work based on the format of the options
We make y the subject of formula:
2x - 5y = 10
subtract 2x from both sides of the equation:
2x - 2x - 5y = 10 - 2x
-5y = 10 - 2x
Rewritting:
-5y = -2x + 10
divide both sides by -5:
-5y/-5 = -2x/-5 + 10/-5
Division of same sign gives positive number. Division of opposite signs give negative number.
y = 2x/5 - 2
2x - 5y = 10 is equivalent to y = 2x/5 - 2 (option B)
1.75k + 1.25 < 3 help
Answers
Answer:
1.75k + 1.25 < 3.
Corrected:
1.75k + 1.25 < 3.
where's the construction of what todo
Shaloo runs along the sides of a square garden which is 85 m long. if she covers 50 cm in one how many steps will she take to run once step. round the garden
Answers
Shaloo will take 680 steps to run once around the garden.
To find the number of steps Shaloo will take to run around the square garden, we need to calculate the perimeter of the garden first. The garden is given to be 85 meters long, and since it is a square, all sides are equal. Therefore, the perimeter of the garden is 4 times the length of one side. Since the length of one side is 85 meters, the perimeter of the garden is 4 * 85 = 340 meters.
Now, we need to convert the distance covered in one step by Shaloo from centimeters to meters. Given that she covers 50 cm in one step, we can convert it to meters by dividing by 100. Thus, one step is equal to 50/100 = 0.5 meters.
To find the number of steps, we divide the perimeter of the garden by the distance covered in one step: 340 meters / 0.5 meters = 680 steps.
To know more about garden visit:
brainly.com/question/22114631
#SPJ11
tiffany walks x miles in 90 minutes. How many miles can she walk in 120 minutes?
A. 4/3 x
B. 30x
C. 3/4
D. 0.75x
Answers
Answer: A. 4/3 x
Step-by-step explanation:
x miles in 90 minutes to ? miles in 120 minutes
90 miles to 120 miles is 1.3333 which is equal to 4/3.
Multiply it to x and you have A. 4/3x
The following sets are defined: - C={ companies },e.g.: Microsoft,Apple I={ investors },e.g.JP Morgan Chase John Doe - ICN ={(i,c,n)∣(i,c,n)∈I×C×Z +
and investor i holds n>0 shares of company c} o Note: if (i,c,n)∈
/
ICN, then investor i does not hold any stocks of company c Write a recursive definition of a function cwi(I 0
) that returns a set of companies that have at least one investor in set I 0
⊆I. Implement your definition in pseudocode.
Answers
A recursive definition of a function cwi (I0) that returns a set of companies that have at least one investor in set I0 is provided below in pseudocode. The base case is when there is only one investor in the set I0.
The base case involves finding the companies that the investor owns and returns the set of companies.The recursive case is when there are more than one investors in the set I0. The recursive case divides the set of investors into two halves and finds the set of companies owned by the first half and the second half of the investors.
The recursive case then returns the intersection of these two sets of def cwi(I0):
companies.pseudocode:
if len(I0) == 1:
i = I0[0]
return [c for (j, c, n) in ICN if j == i and n > 0]
else:
m = len(I0) // 2
I1 = I0[:m]
I2 = I0[m:]
c1 = cwi(I1)
c2 = cwi(I2)
return list(set(c1) & set(c2))
To know more about intersection visit :
https://brainly.com/question/30722656
#SPJ11
HEEEELPPPPPP
-4x – (-3 − 5x) = -3(2x − 8)
Answers
Answer:
x=3
Step-by-step explanation:
U 2 can help me by marking as brainliest.........
Answer:
x = 3
Step-by-step explanation:
-4x - (-3 - 5x) = -3(2x - 8)
=> -4x + 3 + 5x = -6x + 24
=> x + 3 = -6x + 24
=> x + 6x = 24 - 3
=> 7x = 21
=> x = 3
PLEASE HELP !!!!!!??

Answers
Answer:
( 1, 35 )
Step-by-step explanation:
y=mx+c
c= y-intercept ( where the graph line crosses the cross line)
c=0
mx = gradient ( rise/run, up/across )
mx = 175/5 ( you could have picked any point in the graph )
mx = 35
the m is useless now so we discard it
y= 35x+0
if x = 1
then y = 35(1)+0
y= 35
at the coordinate x=1 y is 35
How do you find 15% of 160?
Answers
2) Find 5% = 8
3) Therefore 15% = 10% + 5% = 24
HELPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPP

Answers
Answer:
the trig function you would use to find x would be cosine becuase its adjacent/ hypotenuse.
solving it would give you 49 becuase its cosine(x)=13/20 and you have to multiply by the inverse of cosine
to solve for y you would use sine of y which would be opposite/ hypotenuse = 13/20
Check all statements that are true,
1) In Euclidean geometry, the sum of the angle measures of a triangle is equal to 180°
2) In both Eudidean and spherical geometry, a triangle can have two right angles.
3) In both Euclidean and spherical geometry, through any point not on a given line there is a line
parallel to the given line.
4) In spherical geometry, some quadrilaterals are parallelograms.
5) In spherical geometry, any two given lines must intersect.
6) None of these are true.
Answers
4) In spherical geometry, some quadrilaterals are parallelograms.
In spherical geometry, some quadrilaterals are parallelograms is a true statement. Thus option D is correct.
What is spherical geometry?Instead of the sort of geometries studied in trigonometry or solid geometry, the research of shapes on a structure's surface. White lines are large rounds in spherical, therefore any three layers intersect at two locations.
A spherical quadrilateral is a bounded surface that is homomorphic to a compact disk. It has four distinct local maxima called extremities, a Riemannian measurement that has constant curvature 1 everywhere else, aside from the corners, and or the demarcation arcs between it intersections. a dome shape. the collection of rectangular shapes with specified angles.
Therefore, option D is the correct option.
Learn more about spherical geometry, Here:
https://brainly.com/question/4637858
#SPJ2
Three times Tara's age decreased by 2 years is the same as twice her age increased by 13 years. How old is
Tara?
Answers
The area of the rectangular portion of the window can be represented by the function A(x) = 2x^2 + 10x. The area of the trapezoidal portion can be represented by the function A(t) = 6((x + 15) + (2x + 10)/2). Formulate a function A(w) that can be used to represent the area of the entire window.
A(w) = 9x + 75
A(w) = x(2x + 10)
A(w) = 21x^2 + 75x
A(w) = 2x^2 + 19x + 75
Answers
The function A(w) that can be used to represent the area of the entire window is 2x^2+17x+95.
We have given that,
The area of the rectangular portion of the window can be represented by the function A(x) = 2x^2 + 10x.
The area of the trapezoidal portion can be represented by the function A(t) = 6((x + 15) + (2x + 10)/2).
A(t)=6x+90+x+5
A(t)=7x+95
What is the area of the formula?\(Area\ of \ the\ rectangle=Length \times width\)
Therefore the function A(w) that can be used to represent the area of the entire window is
A(W)=A(t)+A(x)
A(W)=7x+95+2x^2 + 10x
A(W)=2x^2+17x+95
The function A(w) that can be used to represent the area of the entire window is 2x^2+17x+95.
To learn more about the rectangle visit:
https://brainly.com/question/25292087
#SPJ2
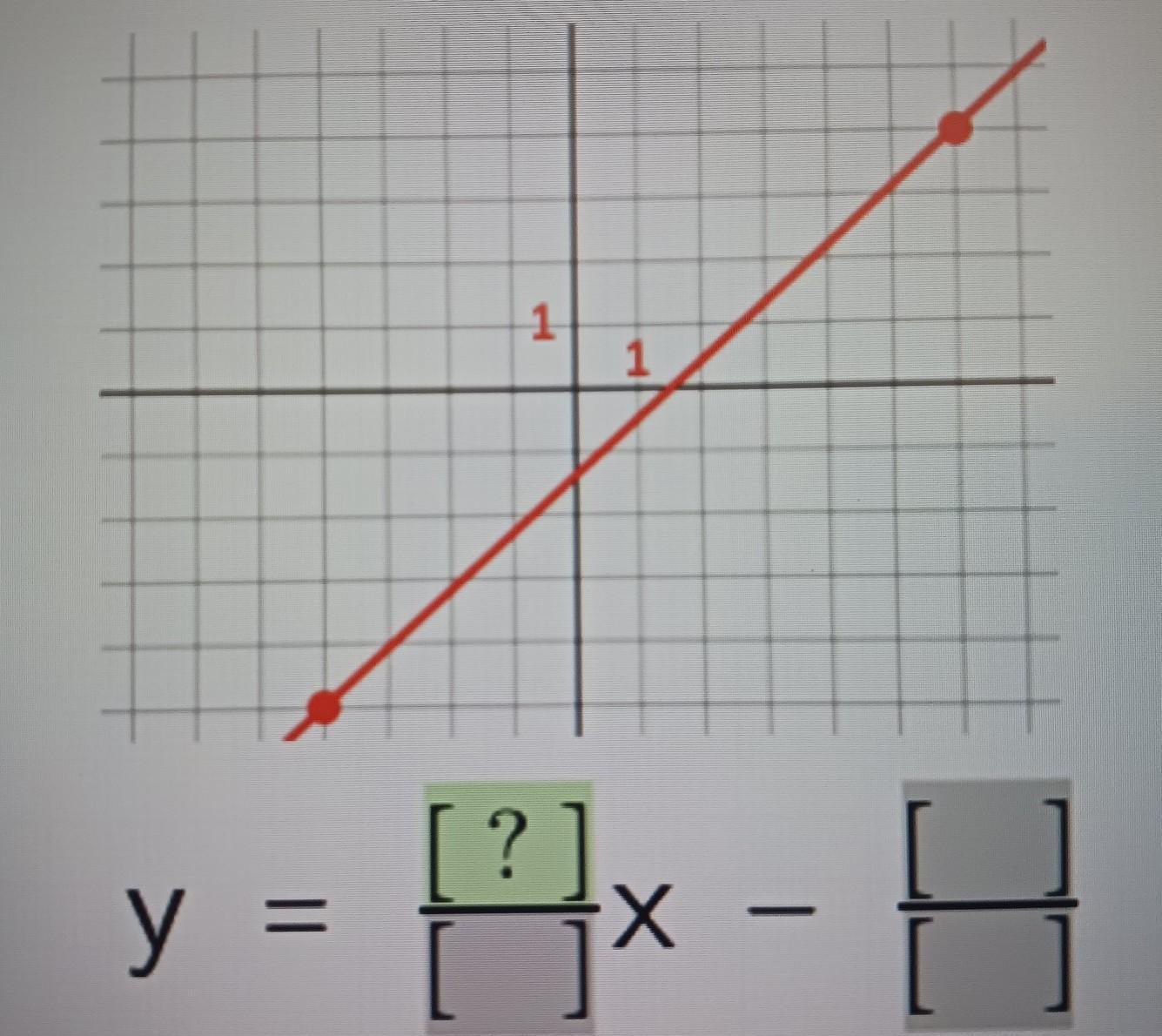
Find the equation of the line.
Answers
Answer:
\(y=\frac{9}{10}x-\frac{7}{5}\)
Step-by-step explanation:
Using the points \((-4,-5)\) and \((6,4)\), the slope is \(m=\frac{-5-4}{-4-6}=\frac{9}{10}\).
Using point-slope form:
\(y+5=\frac{9}{10}(x+4) \\ \\ y+5=\frac{9}{10}x+\frac{18}{5} \\ \\ y=\frac{9}{10}x-\frac{7}{5}\)
The number of boys and girls in a school are in the ratio 5: 7. What is
the number of girls if 1200 boys are there in the school.
Answers
Answer:
There are 1,680 Girls
Step-by-step explanation:
1 ratio = 240
5 ratio = 1,200
7 ratio = 1,680
Therefore, 5:7 = 1,200 : 1,680
In 1994, the moose population in a park was measured to be 3000. By 1998, the population was measuredagain to be 3400. If the population continues to change linearly:Find a formula for the moore population, P, in terms of t, the years since 1990.P(t)-What does your model predict the moose population to be in 2005?
Answers
We will consider a graph
Where x on the graph represent years since 1990 and y on the graph to represent the population of the moose
We have two points on the graph: ( 4, 3000) and (8, 3400)
Using the slope formula;
slope(m) = y₂-y₁ / x₂-x₁
=3400-3000 / 8-4
=400/4
=100
We can now use the slope formula to find the equation for the line;
y- y₁ = m (x- x₁)
y - 3000 = 100( x- 4)
y - 3000= 100x - 400
add 3000 to both-side of the equation
y-3000+3000=100x-400+3000
y= 100x + 2600
But the formula is in term of p and t
Hence, we will replace y by p and then x with t
p(t) = 100t + 2600
Hence, the above is the formula for the Moore population since 1990
To predict the moose population in 2005, we determine the years from 1990 to 2005
years = 2005 - 1990 = 15
substituting into the equation;
p(t) = 100t + 2600
p(15) = 100(15) + 2600
= 1500 + 2600
= 4100
p(15) = 4100
The model predict the moose population to be 4100 in 2005
Type the correct answer in the box. Write your answer as a reduced fraction, using / for the fraction bar.
A six-sided fair die is rolled 4 times in a row. The probability of getting a 4 only on the last trial is
Answers
Answer:
Step-by-step explanation:
P(4 only on the last roll) = P(not 4 on first roll) and P(not 4 on the second roll) and P(not 4 on the third roll) and P(4 on the last roll)
in probability and = multiplication
P( not roll a 4) = 1 - P(roll a 4)
P(4 only on the last roll) = 1-P(4) * 1-P(4) *1-P(4) * P(4)
P(4) = 1 (1 time# 4 appears on the die)/6 (#of possible outcomes 1,2,3,4,5,6)
P(4 only on the last roll) = 1-(1/6) * 1-(1/6) *1-(1/6) * (1/6)
P(4 only on the last roll) =(5*5*5*1)/(6*6*6*6) = 125/1296
Answer: 125/1296
Step-by-step explanation:
The price of one share of a company declined $3.50 per day for 4 days in a row. What is the overall change in the price of one share? You may find using a number line to be helpful.
The overall change in the price of one share is
dollars.
Answers
Leslie invest 42,000 into an account that pays 7%compounded weekly. How much is the account worth after 5 years?
Answers
Answer:
$41,998.58
Step-by-step explanation:
The computation of the account worth after 5 years is shown below:
As we know that
Future value = Present value ×(1+ rate of interest)^number of years
= 42,000 × (1 + 0.07 ÷ 52)^5× 52
= 42,000 × (1 + 0.0013461)^260
= $41,998.58
An entity has the following balances: Bank: R5 000; Machinery: R3 000: Trade payables: R2 000.
The equity of the entity according to the basic accounting equation is …
NB: Instructions
1. Use a full stop to indicate any decimals (eg: 1000.01)
2. Only show the amount, do not show the R (eg: 12141.72)
Answers
The equity of the entity, according to the basic accounting equation, is R6 000. The basic accounting equation is Assets = Liabilities + Equity. To find the equity of the entity, we need to subtract the total liabilities from the total assets.
Bank balance: R5 000
Machinery balance: R3 000
Trade payables: R2 000
Total assets = Bank + Machinery
= R5 000 + R3 000
= R8 000
Total liabilities = Trade payables
= R2 000
Equity = Total assets - Total liabilities
= R8 000 - R2 000
= R6 000
Therefore, the equity of the entity, according to the basic accounting equation, is R6 000.
Learn more about equity here:
brainly.com/question/29436253
#SPJ11
The function:
V(x) = x(10-2x)(16-2x), 0
a) Find the extreme values of V.
b) Interpret any valuse found in part (a) in terms of volumeof the box.
Answers
The minimum value of V occurs at x ≈ 0.93, which means that the volume of the box is smallest when the height is about 0.93 units.
To find the extreme values of V, we need to take the derivative of V and set it equal to zero. So, let's begin:
\(V(x) = x(10-2x)(16-2x)\)
Taking the derivative with respect to x:
\(V'(x) = 10x - 4x^2 - 32x + 12x^2 + 320 - 48x\)
Setting V'(x) = 0 and solving for x:
\(10x - 4x^2 - 32x + 12x^2 + 320 - 48x = 0\\8x^2 - 30x + 320 = 0\)
Solving for x using the quadratic formula:
\(x = (30 ± \sqrt{(30^2 - 4(8)(320))) / (2(8))\\x = (30 ± \sqrt{(1680)) / 16\\x = 0.93 or x =5.07\)
So, the extreme values of V occur at x ≈ 0.93 and x ≈ 5.07. To determine whether these are maximum or minimum values, we need to examine the second derivative of V. If the second derivative is positive, then the function has a minimum at that point. If the second derivative is negative, then the function has a maximum at that point. If the second derivative is zero, then we need to use a different method to determine whether it's a maximum or minimum.
Taking the second derivative of V:
V''(x) = 10 - 8x - 24x + 24x + 96
V''(x) = -8x + 106
Plugging in x = 0.93 and x = 5.07:
V''(0.93) ≈ 98.36 > 0, so V has a minimum at x ≈ 0.93.
V''(5.07) ≈ -56.56 < 0, so V has a maximum at x ≈ 5.07.
Now, to interpret these values in terms of the volume of the box, we need to remember that V(x) represents the volume of a box with length 2x, width 2x, and height x. So, the maximum value of V occurs at x ≈ 5.07, which means that the volume of the box is greatest when the height is about 5.07 units. The minimum value of V occurs at x ≈ 0.93, which means that the volume of the box is smallest when the height is about 0.93 units.
learn more about extreme values
https://brainly.com/question/1286349
#SPJ11
a) The extreme values of V are:
Minimum value: V(0) = 0
Relative maximum value: V(3) = 216
Absolute maximum value: V(4) = 128
b) The absolute maximum value of V at x = 4 represents the case where the box has a square base of side length 4 units, height 2 units, and width 8 units, which has a volume of 128 cubic units.
a) To find the extreme values of V, we first need to find the critical points of the function. This means we need to find where the derivative of the function equals zero or is undefined.
Taking the derivative of V(x), we get:
\(V'(x) = 48x - 36x^2 - 4x^3\)
Setting this equal to zero and solving for x, we get:
\(48x - 36x^2 - 4x^3 = 0\)
4x(4-x)(3-x) = 0
So the critical points are x = 0, x = 4, and x = 3.
We now need to test these critical points to see which ones correspond to maximum or minimum values of V.
We can use the second derivative test to do this. Taking the derivative of V'(x), we get:
\(V''(x) = 48 - 72x - 12x^2\)
Plugging in the critical points, we get:
V''(0) = 48 > 0 (so x = 0 corresponds to a minimum value of V)
V''(4) = -48 < 0 (so x = 4 corresponds to a maximum value of V)
V''(3) = 0 (so we need to do further testing to see what this critical point corresponds to)
To test the critical point x = 3, we can simply plug it into V(x) and compare it to the values at x = 0 and x = 4:
V(0) = 0
V(3) = 216
V(4) = 128
So x = 3 corresponds to a relative maximum value of V.
b) In terms of the volume of the box, the function V(x) represents the volume of a rectangular box with a square base of side length x and height (10-2x) and width (16-2x).
The minimum value of V at x = 0 represents the case where the box has no dimensions (i.e. it's a point), so the volume is zero.
The relative maximum value of V at x = 3 represents the case where the box is a cube with side length 3 units, which has a volume of 216 cubic units.
for such more question on extreme values
https://brainly.com/question/30886356
#SPJ11
The value of R2 always ...
lies below 0
lies above 1
lies between 0 and 1
lies between -1 and +1
Answers
The value of R2 always lies between 0 and 1.The value of R2 represents the proportion of the variation in the dependent variable that can be explained by the independent variables, ranging from 0 to 1.
The value of R2, also known as the coefficient of determination, measures the goodness of fit of a regression model. It represents the proportion of the total variation in the dependent variable that is explained by the independent variables in the model.
R2 ranges between 0 and 1, where 0 indicates that the independent variables have no explanatory power and cannot predict the dependent variable's variation. On the other hand, an R2 value of 1 indicates that the independent variables perfectly explain all the variation in the dependent variable.
An R2 value greater than 1 or less than 0 is not possible because it would imply that the model explains more than 100% or less than 0% of the dependent variable's variation, which is not meaningful. Therefore, the value of R2 always lies between 0 and 1, providing a measure of the model's explanatory power.
To learn more about coefficient, click here:
/brainly.com/question/1594145
#SPJ1
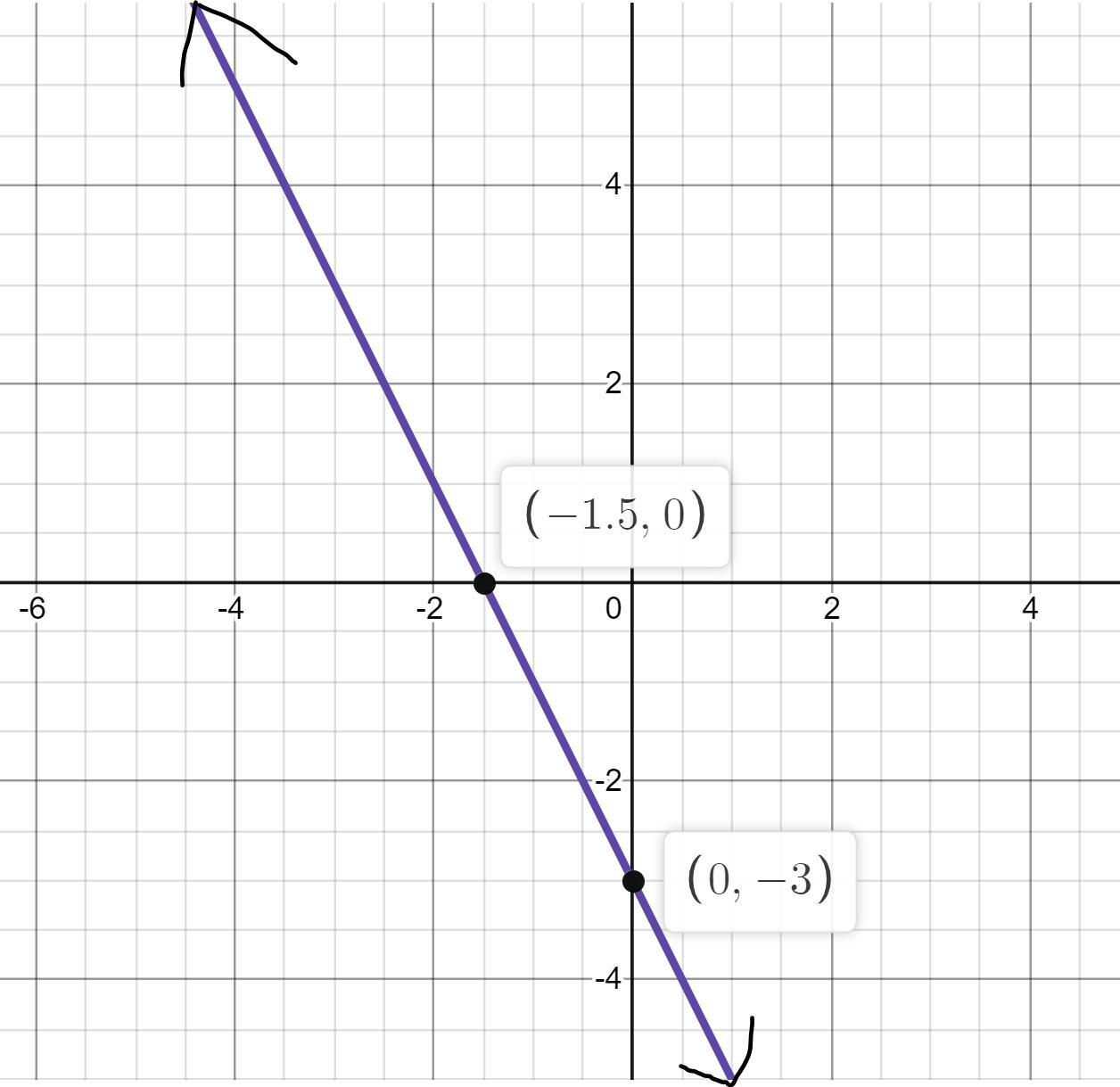
A line has a slope of -2 and a y-intercept of –3. Graph the line using the slope and y-intercept.
Which of the following points lie on this same line? Check all that apply.
(–2, 0)
(–1.5, 0)
(–6, 9)
(2, –3)
(3, –9)
(–4, 4)
Answers
Answer & Step-by-step explanation:
First write the line equation.
y=mx+b is the format where m=slope, b= y intercept
y=-2x-3
plug each x in to see if they match the point
y= -2(-2) -3 = -4 - 3 = -7 ; the point is (-2,0) so NO
y= -2(-1.5) -3= 3-3 = 0; point is (-1.5, 0) so YES it matches
y= -2(-6) -3 = 12-3 = 0; point matches so YES
y= -2(2) -3 = -4-3 = -7; point is (2, -3) so NO
y = -2(3) -3 = -6-3= -9; point matches so YES
y= -2(-4)-3 = 8-3 = 5; point is (-4, 4) so NO
(-1.5, 0) & (-6, 9) & (3, -9)
please give thanks by clicking the heart button :)
Answer:
the answers are B C E
Step-by-step explanation:
-1,5, 0
-6, 9
3, -9
Can someone help me??? Evaluate piecewise functions
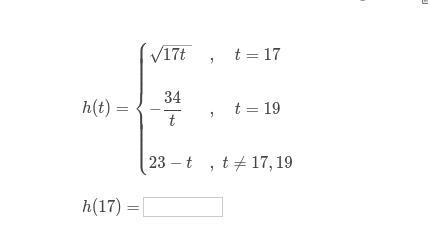
Answers
Answer: 17h
Step-by-step explanation:
H * 17 = 17h
Can somebody plz help answer all the questions correctly thanks!!
WILL MARK BRAINLIEST WHOEVERR ANSWERS FIRST :DD

Answers
Answer:
16.32.5
17.1.32
18.3.25
19.540
20.5.49
21.4.75
Step-by-step explanation:
Answer:
16=$32.5
17=$1.32
18=$3.25
19=$540
20=$5.49
21=$4.75
Step-by-step explanation:trust me bro
In parallelogram best, diagonals bs and et bisect each other at o.
1. if es = 10cm, how long is bt?
2. if be = 13cm, how long is ts?
3. if eo = 6cm and so = 7cm, what is the length of et? bs?
4. if et + bs = 18cm and so = 5cm, find et and bs.
Answers
When the parallelogram, diagonals bs and et bisect at each other at o, we get the following answers:
1. In a parallelogram, the diagonals bisect each other. So, if ES = 10 cm, then EO = OS = 5 cm. Since EO and OS are half of the diagonal ET, then ET = EO + OS = 5 cm + 5 cm = 10 cm. Similarly, diagonal BT will also be equal to 10 cm, as it has the same length as diagonal ET.
2. In a parallelogram, opposite sides are equal. So, if BE = 13 cm, then TS = 13 cm, as they are opposite sides.
3. If EO = 6 cm and SO = 7 cm, then the length of diagonal ET is EO + OS = 6 cm + 7 cm = 13 cm. Since the diagonals of a parallelogram are equal, the length of diagonal BS will also be 13 cm.
4. If ET + BS = 18 cm and SO = 5 cm, we can use the fact that diagonals bisect each other to find ET and BS. Let EO = x cm. Then, ET = 2x cm and BS = 2(5-x) cm. Now, we can set up the equation: 2x + 2(5-x) = 18. Solving for x, we get x = 4 cm. So, ET = 2x = 8 cm and BS = 2(5-x) = 10 cm.
To learn more about diagonal, refer below:
https://brainly.com/question/12274248
#SPJ11
PLEASEEEEEE HELPPPPPPPPP

Answers
\(5x + 3 = - 9 \\ = > 5x = - 9 - 3 \\ = > 5x = - 12 \\ = > x = \frac{ - 12}{5} \\ = > x = - 2 \frac{2}{5} \)
Answer:Option A .
\( - 2 \frac{2}{5} \)
If someone could please answer this for me it’s 9th grade math 12 points:) asap pleaseee

Answers
I just copied what the other person said because I'm not in 9th grade lol
A side of the triangle below has been extended to form an exterior angle of
67º. Find the value of x.
52
xº
67°
Answers
The value of x in the given triangle is 61 degrees.
In the given triangle, we have an exterior angle of 67 degrees formed by extending one side of the triangle. Let's label the interior angles of the triangle as A, B, and C, with angle A being the exterior angle of 67 degrees.
According to the property of exterior angles of a triangle, the exterior angle is equal to the sum of the two interior opposite angles. Therefore, we have the equation:
A = B + C
Substituting the given values, we have:
67° = B + C
Now, we can observe that angle C is the interior angle labeled as x degrees. So we rewrite the equation as:
67° = B + x
Since the sum of the interior angles in a triangle is always 180 degrees, we have the equation:
A + B + C = 180°
Substituting the given values and rearranging the equation, we get:
67° + B + x = 180°
Simplifying further:
B + x = 180° - 67°
B + x = 113°
Now, we can equate the two expressions for B + x:
B + x = 113°
Since B is given as 52 degrees, we can substitute this value:
52° + x = 113°
Subtracting 52 from both sides, we find:
x = 113° - 52°
x = 61°
Therefore, the value of x in the given triangle is 61 degrees.
Learn more about exterior angle here:
https://brainly.com/question/28835566
#SPJ11