Quadrilateral WXYZ is a rectangle.
If X W=3, W Z=4 , and X Z=b , find Y W .
Answers
The length of the diagonal YW of rectangle WXYZ is; 5 units.
How to find the diagonals of a rectangle?
The diagonals of a rectangle are congruent and so;
YW ≅ XZ
Thus; YW = XZ = b
Now, given the three sides of right triangle XWZ, we can solve for XZ using Pythagorean Theorem:
(XW)² + (WZ)² = (XZ)²
Plugging in the relevant values gives;
3² + 4² = b²
9 + 16 = b²
25 = b²
b = √25
b = 5
Thus, we can conclude that the length of the diagonal YW is 5 units.
Read more about Pythagoras Theorem at; https://brainly.com/question/231802
#SPJ1
Related Questions
Given that h=m²-h/2k rewrite the formula by making m the subject of the formula.
Answers
With given h= \(\frac{m^2 -h}{2k}\), after rewriting the formula by making m the subject, it will be, \(\sqrt{h(2k+1)}\).
Given,
h= \(\frac{m^2 -h}{2k}\) ......... (i)
⇒h×2k =\(m^2 -h\)
⇒\(m^2\) =2kh+h.
⇒\(m^2\)= h×(2k+1)
⇒m=\(\sqrt{h(2k+1)}\) ....................................(ii)
Now in this equation m is the subject.
Read more about the equation,
https://brainly.com/question/29174899
if x=5, y=-3, and z=-7 z=-7, evaluate 3x^2-9y/yz
Answers

how many elementary events are in the sample space of the experiment of rolling three fair coins?
a.2
b.9
c.8
d.6
Answers
The sample space of the experiment of rolling three fair coins consists of all possible outcomes when three coins are tossed simultaneously. Therefore, there are 2 x 2 x 2 = 8 possible outcomes in the sample space.
In this experiment, we are rolling three fair coins. To find the number of elementary events in the sample space, we need to consider all possible outcomes.
An elementary event is an individual outcome in the sample space. The sample space is the set of all possible outcomes for an experiment. In this case, each coin can have 2 possible outcomes: heads (H) or tails (T).
Each outcome in the sample space is an elementary event, which is an outcome that cannot be further broken down into simpler outcomes. Therefore, there are 8 elementary events in the sample space of this experiment.
Since there are three coins, we can determine the number of elementary events in the sample space by multiplying the number of outcomes for each coin: 2 (for the first coin) x 2 (for the second coin) x 2 (for the third coin) = 8.
So, there are 8 elementary events in the sample space of this experiment. The correct answer is c. 8.
Learn more about sample space:
brainly.com/question/30206035
#SPJ11
A recent study reported that 60% of the children in a particular community were overwoight or obese. Suppose a random sample of 200 public school children is taken from this community. Assume the sample was taken in such a way that the conditions for using the Central Limit Theorem are met. We are interested in finding the probability that the proportion of overveightfobese children in the sample will be greater than 0.57. Complete parts (a) and (b) below. a. Before doing any calculations, determine whether this probability is greater than 50% or less than 50%. Why? A. The answer should be less than 50%. because 0.57 is less than the population proportion of 0.60 and because the sampling distribution is approximately Normal. B. The answer should be greater than 50%, because the resulting z-score will be positive and the sampling distribution is approximately Normal. C. The answer should be greater than 50%, because 0.57 is less than the population proportion of 0.60 and because the sampling distribution is approximately Normal. 0. The answer should be less than 50%, because the resulting z-score will be negative and the sampling distribution is approximately Normal.
Answers
The probability that the proportion of overweight or obese children in the sample will be greater than 0.57 is less than 50%.
The first paragraph summarizes the answer, stating that the probability is less than 50% because 0.57 is less than the population proportion of 0.60, and the sampling distribution is approximately normal.
In the second paragraph, we can explain the reasoning behind this conclusion. The Central Limit Theorem states that for a large sample size, the sampling distribution of the sample proportion will be approximately normal, regardless of the shape of the population distribution. In this case, the sample was taken in a way that meets the conditions for using the Central Limit Theorem.
Since the population proportion of overweight or obese children is 0.60, any sample proportion below this value is more likely to occur. Therefore, the probability of obtaining a sample proportion greater than 0.57 would be less than 50%. This is because the resulting z-score, which measures how many standard deviations the sample proportion is away from the population proportion, would be negative.
To summarize, the probability of the proportion of overweight or obese children in the sample being greater than 0.57 is less than 50% because 0.57 is less than the population proportion of 0.60, and the sampling distribution is approximately normal.
To learn more about probability click here, brainly.com/question/31828911
#SPJ11
Taylor kept track of the number of hours that he spent at the media center each week for several weeks. He spent 8, 2, 5, 10, and 5 hours.
Answers
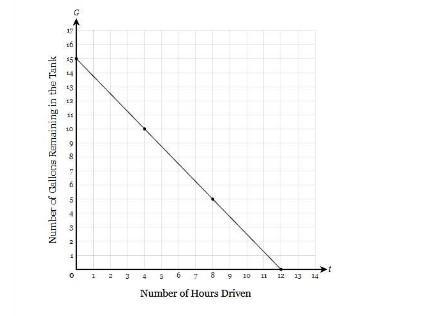
Serenity filled up her car with gas before embarking on a road trip across the country. Let � G represent the number of gallons of gas remaining in her gas tank after driving for � t hours. A graph of � G is shown below. Write an equation for � G then state the � y-intercept of the graph and determine its interpretation in the context of the problem.
Answers
The equation is: G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
How to find the linear equation of the graph?The formula for the equation of a line in slope intercept form is:
y = mx + c
where:
m is slope
c is y-intercept
From the graph, we see that:
y-intercept = 15 gallons
Now, the slope is gotten from the formula:
Slope = (y₂ - y₁)/(x₂ - x₁)
Slope = (10 - 5)/(4 - 8)
Slope = -⁵/₄
Thus, equation is:
G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
Read more about Linear equation graph at: https://brainly.com/question/28732353
#SPJ1
Kathy is a scientist who is working in a remote part of Australia. She earns a salary of $86 840 plus a weekly allowance of $124.80 for working under extreme and isolated conditions. Calculate Kathy’s fortnightly pay.
Answers
Answer:
$3589.60
Step-by-step explanation:
Salary per fortnight {52 weeks in a year; 2 weeks in a fortnight}
= 86840 / 52 × 2
= 3340
Allowance per fortnight = 124.80 × 2 = 249.60
Therefore, total fortnightly pay is:
3340 + 249.60 = 3589.60
What is the polar equation of the graph below
Select one:
r = 5cos40
O b. r=
4cos50
O c. r = 4sin50
O d. r = 4cos100
a.
Answers
The polar equation of the graph shown below include the following: B. r = 4cos5θ.
How to graph a polar equation?In Mathematics and Geometry, the relationship between a polar coordinate (r, θ) and a rectangular coordinate (x, y) based on the conversion rules is given by the following polar equations:
a = rcos(θ) ....equation 1.
b = rsin(θ) ....equation 2.
Where:
θ is the angle.r is the radius of a circle.By critically observing the graph of this polar equation, we can logically conclude that it represents a rose and it is symmetric with respect to the polar axis;
-r = -4cos5(π - θ)
-r = -4cos(5π - 5θ)
-r = 4cos(-5θ)
-r = -4cos(5θ)
r = 4cos(5θ)
In conclusion, the graph shown below can be modeled by this polar equation r = 4cos(5θ).
Read more on polar coordinates here: brainly.com/question/32313794
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.

Witch of the s-values satisfy the following inequality?
7-s/2>3
Choose all answers that apply:
A 8 = 6
B 8 =8
C 8= 10

Answers
Answer:
the possible answer would be A, 6.
Step-by-step explanation:
6/2 is equal to 3 wholes. 7 minus 3 is 4. the sign > is used to indicate that the left number is greater than the right number, which is 3. 4 > 3 would be shown. this means that 6, or A, is the answer! :)
(6 IS ALSO THE ONLY OPTION. I NOTICED IT SAYS “ALL ANSWERS“
24. Seven tenths of a number plus 14 is less than forty-nine.
Answers
Answer:
50. ☺️☺️
Step-by-step explanation:
I'm going to assume you need this inequality solved.
First, write it as numbers, not words.
7/10n + 14 < 49
where "n" is the unknown number.
Second, if I were you, I'd change that fraction into a decimal, as it'll make life easier later on.
7/10 = 0.7
Now, solve it like you would any other equation.
0.7n + 14 < 49
0.7n +14 - 14 < 49 - 14
0.7n < 35
0.7n ÷ 0.7 < 35 ÷ 0.7
n < 50
The answer is n < 50
Answer: 50
Step-by-step explanation:
49 - 14 = 35
35/7 = 5
10 x 5 = 50
Since, 35 is Seven tenths of a number, One tenth is 5 and there are ten tenths, One tenth which is 5 times ten since there are ten tenths equals to 50 (5 x 10 = 50).
Which expression is equivalent to 7(d - 4)?
Submit
7(-4+ d)
-4(d + 7)
(d + 7).-4
-28d + 7
Answers
The phrase that is identical to 7(d - 4) in option B is -4(d+ 7). A mathematical expression is a statement that contains a minimum of two numbers .
what is expression ?A mathematical expression is a phrase having a minimum of two numbers or variables and at least one mathematical operation. This mathematical operation may be addition, subtraction, multiplication, or division. An expression's basic components are as follows: Expression is (Number/Variable, Math Operator, Number/Variable). A mathematical expression is a statement that contains a minimum of two numbers or variables and at least one mathematical operation. Let's learn how to write expressions. A number is 6 more than half of another number, and that other number is called x. In a mathematical expression, this statement is represented as x/2 + 6.
given
The correct response is 4 less than 7, since 4 is less than 7.
Thus, 7-4=3 could be considered.
The first section of 7–4 appears to be answer B.
The phrase that is identical to 7(d - 4) in option B is -4(d+ 7).
To know more about expression visit :-
https://brainly.com/question/14083225
#SPJ1
Find the exact value of cos J in simplest form.
√29
14
15
H
Answers
The cosine of angle J is given as follows:
\(\cos{J} = \frac{14\sqrt{2}}{49}\)
What are the trigonometric ratios?The three trigonometric ratios are the sine, the cosine and the tangent of an angle, and they are obtained according to the rules presented as follows:
Sine = length of opposite side/length of hypotenuse.Cosine = length of adjacent side/length of hypotenuse.Tangent = length of opposite side/length of adjacent side = sine/cosine.For the angle J in this problem, we have that:
4 is the adjacent side.\(\sqrt{98}\) is the hypotenuse.Hence the cosine of angle J is given as follows:
\(\cos{J} = \frac{4}{\sqrt{98}} \times \frac{\sqrt{98}}{\sqrt{98}}\)
\(\cos{J} = \frac{4\sqrt{98}}{98}\)
\(\cos{J} = \frac{2\sqrt{98}}{49}\)
As 98 = 2 x 49, we have that \(\sqrt{98} = \sqrt{49 \times 2} = 7\sqrt{2}\), hence:
\(\cos{J} = \frac{14\sqrt{2}}{49}\)
A similar problem, also about trigonometric ratios, is given at brainly.com/question/24349828
#SPJ1

The Robot Factory is a learning center where children can build robots. The project fee per visit is $18, and each hour of time (x) at the factory costs $6. Jesse goes to the Robot Factory one afternoon, and the total charge for his visit is $33. Write and solve and equation to find the number of hours Jesse spent at the Robot Factory.
Answers
Answer:
equation=33=6x+18
Step-by-step explanation:
33=6x+18
-18 -18
15/6=6x/6
15/6=x
2.5 hours at the robot factory
Kevin bought 30 pounds of flour for $12.
How many pounds of flour did he get per dollar?
Answers
Answer:
2.5
Step-by-step explanation:
pounds/dollar = 30pounds/12dollars = 2.5
A firm produces two goods in quantities x and y. Its cost function is C(x,y) = 10x + xy + 10y and the prices P, and P, it can charge are, respectively, Ps = 50 - x + y and Py = 50 - x + y. The firm is committed to delivering a total of 15 units. How much should the firm produce of each good to maximize profits?
Answers
To maximize profits, the firm should produce a quantity of goods x = 5 and y = 10, based on the cost function and price constraints.
To maximize profits, the firm needs to find the quantities of goods x and y that will yield the highest profit. The profit function can be defined as the revenue minus the cost. Revenue is calculated by multiplying the quantity of each good produced with their respective prices, while the cost function is given as C(x, y) = 10x + xy + 10y.
The firm is committed to delivering a total of 15 units, which can be expressed as x + y = 15. To determine the optimal production quantities, we need to maximize the profit function subject to this constraint.
By substituting the price expressions Ps = 50 - x + y and Py = 50 - x + y into the profit function, we obtain the profit equation. To find the maximum profit, we can take the partial derivatives of the profit equation with respect to x and y, set them equal to zero, and solve the resulting system of equations.
Solving the equations, we find that the optimal production quantities are x = 5 and y = 10, which maximize the firm's profits.
Learn more about Partial derivatives click here :brainly.com/question/28376218
#SPJ11
Please help 60 points for a rapid answer-In the figure below which of the following is true in circle E?


Answers
Answer:
all 3 options are true : A, B, C
Step-by-step explanation:
warning : it has come to my attention that some testing systems have an incorrect answer stored as right answer for this problem.
they say that A and C are correct.
but I am going to show you that if A and C are correct, then also B must be correct.
therefore, my given answer above is the actual correct answer (no matter what the test systems say).
originally the information about the alignment of the point F in relation to point E was missing.
therefore, I considered both options :
1. F is on the same vertical line as E.
2. F is not on the same vertical line as E.
because of optical reasons (and the - incomplete - expected correct answers of A and C confirm that) I used the 1. assumption for the provided answer :
the vertical line of EF is like a mirror between the left and the right half of the picture.
A is mirrored across the vertical line resulting in B. and vice versa.
the same for C and D.
this leads to the effect that all 3 given congruence relationships are true.
if we consider assumption 2, none of the 3 answer options could be true.
but if the assumptions are true, then all 3 options have to be true.
now, for the "why" :
remember what congruence means :
both shapes, after turning and rotating, can be laid on top of each other, and nothing "sticks out", they are covering each other perfectly.
for that to be possible, both shapes must have the same basic structure (like number of sides and vertices), both shapes must have the same side lengths and also equally sized angles.
so, when EF is a mirror, then each side is an exact copy of the other, just left/right being turned.
therefore, yes absolutely, CAD is congruent with CBD. and ACB is congruent to ADB.
but do you notice something ?
both mentioned triangles on the left side contain the side AC, and both triangles in the right side contain the side BD.
now, if the triangles are congruent, that means that each of the 3 sides must have an equally long corresponding side in the other triangle.
therefore, AC must be equal to BD.
and that means that AC is congruent to BD.
because lines have no other congruent criteria - only the lengths must be identical.
In circle G with m<FJH=31° , Find the angle measure of minor arc FH

Answers
Answer:
62°
Step-by-step explanation:
Inscribed Angle Theorem
Inscribed angles measures are 1/2 of the arc they create.
m∠FJH x 2 = arc FH
Just take the 31° and double it.
if amount is 7,500, time is 2years and rate is 10% then find principal?
Answers
Answer:
Principal = $9,152.93
Step-by-step explanation:
A = $9,152.93
A = P + I where
P (principal) = $7,500.00
I (interest) = $1,652.93
Calculation Steps:
First, convert R as a percent to r as a decimal
r = R/100
r = 10/100
r = 0.1 rate per year,
Then solve the equation for A
A = P(1 + r/n)nt
A = 7,500.00(1 + 0.1/12)(12)(2)
A = 7,500.00(1 + 0.008333333)(24)
A = $9,152.93
Summary:
The total amount accrued, principal plus interest, with compound interest on a principal of $7,500.00 at a rate of 10% per year compounded 12 times per year over 2 years is $9,152.93.
If a rocket in space is moving at a constant velocity of 9. 8 m/s and then uses its propulsion system to accelerate to 10. M/s during a 3. 0 second burn, what would be the acceleration of the rocket?
Answers
The acceleration of the rocket is 0.2 m/s^2.
We can use the equation for average acceleration to find the acceleration of the rocket:
a = (v_f - v_i) / t
where a is the acceleration, v_f is the final velocity, v_i is the initial velocity, and t is the time over which the acceleration occurs.
In this case, the initial velocity is 9.8 m/s, the final velocity is 10 m/s, and the time is 3.0 seconds. Plugging in these values, we get:
a = (10 m/s - 9.8 m/s) / 3.0 s
Simplifying, we get:
a = 0.2 m/s^2
To learn more about acceleration here:
https://brainly.com/question/30595529
#SPJ4
Which fraction represents the slope formula for the line containing (4, 9) and (0, 5)?
Answers
The fraction which represents the slope formula for the line is equal to \(\frac{4}{4}\).
Given the following data:
Points on x-axis = (4, 0)
Points on y-axis = (9, 5).
What is a slope?The slope of a line can be defined as the gradient of a line and it's typically used to describe both the ratio, direction and steepness of an equation of a straight line.
How to calculate the slope of a line.Mathematically, the slope of a line is given by the following formula;
\(Slope, m = \frac{Change\;in\;y\;axis}{Change\;in\;x\;axis}\\\\Slope, m = \frac{y_2\;-\;y_1}{x_2\;-\;x_1}\)
Substituting the given parameters into the formula, we have;
\(Slope, m = \frac{9\;-\;5}{4\;-\;0}\\\\Slope, m = \frac{4}{4}\)
Read more on slope here: brainly.com/question/3493733
Please Help me - You will get 60 points for the rapid reply- Use isosceles trapezoid ABCD to determine the following measurements-

Answers
Answer:
1) AD = 9 in
2) DE = 9.25 in
3) ∠EDC = 36°
4) ∠AEB = 108°
5) 11.5 in
Step-by-step explanation:
1) AD = BC = 9in
2) AC = BD (diagonals are equal)
⇒ BD = 14.25
⇒ BE + DE = 14.25
⇒ 5 + DE = 14.25
DE = 9.25
3) Since AB ║CD,
∠ABE = ∠EDC = 36°
4) ∠ABE = ∠BAE = 36°
Also ∠ABE + ∠BAE + ∠AEB = 180 (traingle ABE)
⇒ 36 + 36 + ∠AEB = 180
∠AEB = 108
5) midsegment = (AB + CD)/2
= (8 + 15)/2
11.5
what will be the value of x after the following code is executed? int x = 10; for (int y=5; y<20; y = 5) x = y;
Answers
The value of x after the following code 'int x = 10; for (int y=5; y<20; y = 5) x = y' is executed will be 5.
The given for loop initializes the variable y to 5, then checks if y is less than 20, and then sets y to 5 again in each iteration. This means that the loop will execute only once with the value of y being 5, and after that, the loop condition will always be false because y is never incremented or changed in any way.
During the execution of the loop, the value of y is assigned to the variable x. Therefore, after the loop, the value of x will be 5.
So, the final value of x will be 5.
For more questions on Algebra
https://brainly.com/question/432678
#SPJ4
What is next year's expected cash flow if there is a 50/50 probability that it will be either $10 million or $60 million?
Answers
The next year's expected cash flow if there is a 50/50 probability that it will be either $10 million or $60 million is $35 million.
What is probability?Probability refers to possibilities. This branch of mathematics deals with the occurrence of a random event. The value's range is 0 to 1. The probability formula states that the ratio of positive outcomes to all other outcomes determines how likely an event is to occur.
Sum of outcomes= 410+$60=$70 million
Number of outcomes=2
As the probability is 50/50, the next year’s expected cash flow will be
10+60/(2)
=70/2
=35 million dollars.
To learn more about probability, visit: https://brainly.com/question/9793303
#SPJ4
I need help with this ASAP, please.

Answers
Answer:
Step-by-step explanation:
2x - y = -8
3x + y = -2
5x = -10
x = -2
3(-2) + y = -2
-6 + y = -2
y = 4
(-2, 4)
Answer: (-2, 4)
Good luck!
Find the equation that intersects the x-axis at point (3, 0) and
intersects the y-axis at
point (0, 5). Then sketch the diagram.
Answers
The equation of the line that intersects the x-axis at point (3, 0) and intersects the y-axis at point (0, 5) is y = (-5/3)x + 5.
To find the equation of a line that intersects the x-axis at point (3, 0) and intersects the y-axis at point (0, 5), we can use the slope-intercept form of a linear equation, which is y = mx + b. Given the point (3, 0) on the x-axis, we know that when x = 3, y = 0. This gives us one point on the line, and we can use it to calculate the slope (m).
Using the slope formula: m = (y2 - y1) / (x2 - x1)
Substituting the values (0 - 5) / (3 - 0) = -5 / 3
So, the slope (m) is -5/3. Now, we can substitute the slope and one of the given points (0, 5) into the slope-intercept form (y = mx + b) to find the y-intercept (b).
Using the point (0, 5):
5 = (-5/3) * 0 + b
5 = b
The y-intercept (b) is 5. Therefore, the equation of the line that intersects the x-axis at point (3, 0) and intersects the y-axis at point (0, 5) is:
y = (-5/3)x + 5
To sketch the diagram, plot the points (3, 0) and (0, 5) on the x-y plane and draw a straight line passing through these two points. This line represents the graph of the equation y = (-5/3)x + 5.
To know more about equation,
https://brainly.com/question/28164076
#SPJ11
a researcher obtain a statistically significant r=-.91 when n=30. how would you report this?
Answers
A statistically significant negative correlation coefficient of r = -0.91 was obtained from a sample of n = 30. This indicates a strong and significant negative relationship between the variables.
The researcher conducted a correlation analysis and found a correlation coefficient (r) of -0.91, which indicates a strong negative relationship between the variables under investigation. The negative sign indicates that as one variable increases, the other variable tends to decrease, and vice versa.
The statistical significance of the correlation coefficient is crucial in determining whether the observed relationship is likely to be due to chance or if it truly exists in the population. In this case, the report should highlight that the obtained correlation coefficient is statistically significant.
To establish statistical significance, the researcher likely conducted a hypothesis test, such as a t-test or a permutation test, to determine the probability of obtaining a correlation coefficient as extreme as -0.91 under the null hypothesis of no correlation. Since the obtained correlation coefficient is statistically significant, it suggests that the observed negative relationship is unlikely to be a result of chance and provides evidence for a genuine association between the variables in the population from which the sample was drawn.
Reporting this finding is important for conveying the strength and significance of the negative relationship to the readers, providing valuable insights for further analysis and interpretation of the variables under investigation.
Learn more about correlation coefficient here:
https://brainly.com/question/29704223
#SPJ11
Help please and thank you

Answers
Answer:
B) 60
Step-by-step explanation:
180-46= 134
134-74= 60
What must be true about two nonzero integers that combine to equal zero?
Answers
Which expression is equivalent to –3 – 3x – 1 x? 2x – 4 –2x 4 –2x – 4? 4 – 2x
Answers
The expression equivalent to -3 - 3x -1x is 4 - 2x.
An expression in math is a sentence with a minimum of two numbers or variables and at least one math operation. This math operation can be addition, subtraction, multiplication, or division. For example, x + y is an expression, where x and y are terms having an addition operator in between. In math, there are two types of expressions, numerical expressions - that contain only numbers; and algebraic expressions- that contain both numbers and variables.
To get to this you can combine like terms:
-3 - 3x - 1x = -3 - (3x + 1x)
= -3 - (4x)
= -3 - 4x
= -4x - 3
= 4 - 2x
Hence 4 - 2x is equivalent to -3 - 3x -1x
To learn more about expression visit -
brainly.com/question/14083225
#SPJ4
A randomly selected group of 35 adult American men (subscript M) was asked if they owned a handgun. 20 said yes. A randomly selected group of 40 adult American women (subscript W) was asked if they owned handgun. 21 said yes. Test the claim that the proportion of adult men who own handguns is the same as the proportion of adult women who own handguns. Use a = .05. Express the claim in symbolic form. a. PM-Pw=0 b. PM-Pw30 c. PM-PW<0 d. PM-Pw>0 e. PM-Pw20 f. PM-PW70
Answers
The claim that the proportion of adult men who own handguns is the same as the proportion of adult women who own handguns is PM-PW=0 the correct answer is option a
To test the claim that the proportion of adult men who own handguns is the same as the proportion of adult women who own handguns, we can use a hypothesis test. Let's define the following variables:
PM = Proportion of adult men who own handguns
PW = Proportion of adult women who own handguns
The claim that the proportions are the same can be expressed as:
Null hypothesis (H0): PM = PW
Alternative hypothesis (H1): PM ≠ PW
Now, we need to perform the hypothesis test using the given data. We can use the two-proportion z-test for this purpose. The formula for the test statistic is:
z = (p1 - p2) / sqrt(p * (1 - p) * (1/n1 + 1/n2))
Where:
p1 = proportion of men who own handguns = 20/35 ≈ 0.571
p2 = proportion of women who own handguns = 21/40 = 0.525
n1 = sample size of men = 35
n2 = sample size of women = 40
p = (p1 * n1 + p2 * n2) / (n1 + n2)
Using the given values, we can calculate the test statistic:
z = (0.571 - 0.525) / sqrt(0.549 * (1 - 0.549) * (1/35 + 1/40)) ≈ 0.466
To determine if this test statistic is statistically significant, we compare it to the critical value corresponding to a significance level (α) of 0.05. Since the alternative hypothesis is two-sided (PM ≠ PW), we will perform a two-tailed test.
Looking up the critical value from the standard normal distribution table, we find that the critical z-value for a two-tailed test with α = 0.05 is approximately ±1.96.
Since the calculated test statistic of 0.466 does not exceed the critical value of ±1.96, we fail to reject the null hypothesis. This means that there is not enough evidence to support the claim that the proportion of adult men who own handguns is different from the proportion of adult women who own handguns.
Therefore, the correct answer is option a. PM-PW=0, as it represents the null hypothesis that the proportions are equal.
To learn more about proportion click here:
https://brainly.com/question/1496357#
#SPJ11