=
Given g(x) = -x +4, solve for x when g(x) = -3.
Answers
9514 1404 393
Answer:
x = 7
Step-by-step explanation:
Put -3 where g(x) is and solve the resulting equation for x.
g(x) = -x +4
-3 = -x +4
x -3 = 4 . . . . . . add x (so we can work with a positive coefficient
x = 7 . . . . . . . . add 3
Answer:
x=-7 i guess
Step-by-step explanation:
Related Questions
Jean wants to save up to put a $2,000 down pay payment on a car. If he deposits $1,800 in an account that earns 4.8% interest compounded monthly, how long will it take for the account to. reach $2,000 Round to the hundredths place.
I am lost
Answers
\(~~~~~~ \textit{Compound Interest Earned Amount} \\\\ A=P\left(1+\frac{r}{n}\right)^{nt} \quad \begin{cases} A=\textit{accumulated amount}\dotfill & \$ 2000\\ P=\textit{original amount deposited}\dotfill &\$1800\\ r=rate\to 4.8\%\to \frac{4.8}{100}\dotfill &0.048\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{monthly, thus twelve} \end{array}\dotfill &12\\ t=years \end{cases}\)
\(2000 = 1800\left(1+\frac{0.048}{12}\right)^{12\cdot t} \implies \cfrac{2000}{1800}=(1.004)^{12t}\implies \cfrac{10}{9}=1.004^{12t} \\\\\\ \log\left( \cfrac{10}{9} \right)=\log(1.004^{12t})\implies \log\left( \cfrac{10}{9} \right)=t\log(1.004^{12}) \\\\\\ \cfrac{\log\left( \frac{10}{9} \right)}{\log(1.004^{12})}=t\implies 2.20\approx t\qquad \textit{about 2 years and 73 days}\)
what is reciprocal of the fraction in the equation 3/5(2x+8)=18?
Answers
9514 1404 393
Answer:
5/3
Step-by-step explanation:
The reciprocal of any fraction is obtained by swapping the numerator and denominator, turning it "upside down."
the reciprocal of the fraction 3/5 is 5/3
-12.40 in simplest from
Answers
Answer: \(- \frac{62}{5}\)
Convert the decimal number into a fraction
Multiply by 10
\((- \frac{12.40}{1} ) (\frac{10}{10})\)
\(- \frac{124}{10}\)
Divide the fraction by 2
\(- \frac{62}{5}\)
Question 9 ONLY!!! Please show work!!

Answers
Step-by-step explanation:
Andrew paid 30% in taxes, which means he has 70% remaining
30% Cash Prize + 70% Cash Prize = 100% Cash Prize
If C = Original Cash Price
Remaining Cash = 70% x C = $28,000
C = $28,000 / 70% = 28000/0.7 = $40,000
I just need a favor please use pemdas and if you can write your work thank you so much

Answers
Answer:
Do you need all 6 of them?
Answer and Step-by-step explanation:
w = -1
x = 6
y = 3
z = -2
32. Plug -2 for z and 6 for x.
(9(-2)) / 6
-18 / 6
3
33.
\(6^{2} - 3^{2}\)
36 - 9
27
34.
\(3^{2} - (-2)^{2}\)
9 - 4
5
35.
\(\frac{2(6)+3}{-2 + -1} \\\\\frac{12+3}{-3}\\\\\frac{15}{3} \\\\5\)
36.
\(\frac{3(6)-(-2)}{-(-1)} \\\\\frac{18 + 2)}{1)} \\\\\frac{20}{1} \\\\20\)
37.
\(\frac{6 + -1}{3 - (-2)} \\\\\frac{5}{5}\\\\1\)
#teamtrees #WAP (Water And Plant) #SPEW (Society for the Promotion of Elfish Welfare)
Can anyone explain how to simplify the square root of 20, in a simple and detailed way?
Answers
Accoreding to the given statement,
The simple method to find the value of √20 is to factorise the number under the root.
What is Factorisation?The process of breaking or decomposing an entity (such as a number, a matrix, or a polynomial) into a product of another entity, or factors, whose multiplication results in the original number, matrix, etc., is known as factorisation or factoring.
According to the given value;
The prime factorisation of 20 = 2 x 2 x 5 = 2 2 x 5
Thus, here we can see, 20 is not a perfect square, because we cannot pair digit 5 after factoring 20.
Only 2 2 can be taken out of the root.
To know more about Factorisation, visit
https://brainly.com/question/20293447
#SPJ9
Solve the following:
A man borrowed a Rs 5000 from a money lender for 5 years at the rate of 8% per annum. How much interest did he pay for 5 years? Also find the amount.
Answers
Answer:
Interest = Rs 2000
Amount = Rs 7000
Step-by-step explanation:
Amount = Principal + Interest
Given
Principal = Rs 5000
Interest= PRT/100
Interest = 5000*8*5/100
Interest = 50*40
Interest = Rs 2000
Amount after 5years = 5000 + 2000
Amount after 5years = Rs 7000
If DEF Is equivalent to GHF, what is the value of X?

Answers
The value of x is 19.44
What are similar triangles?Similar triangles are triangles that have the same shape, but their sizes may vary.
For two triangles to be similar, the corresponding angles must be congruent and also, the ratio of the corresponding sides of similar triangles are equal,
therefore,
27/9x-13 = 15/90
27 × 90 = 15(9x-13)
2430 = 135x - 195
collecting like terms
2430+195 = 135x
2625 = 135x
divide both sides by 135
x = 2625/135
x = 19.44
therefore the value of x is 19.44
learn more about similar triangles from
https://brainly.com/question/14285697
#SPJ1
3
2-
-2
7777
-3
2 3 456
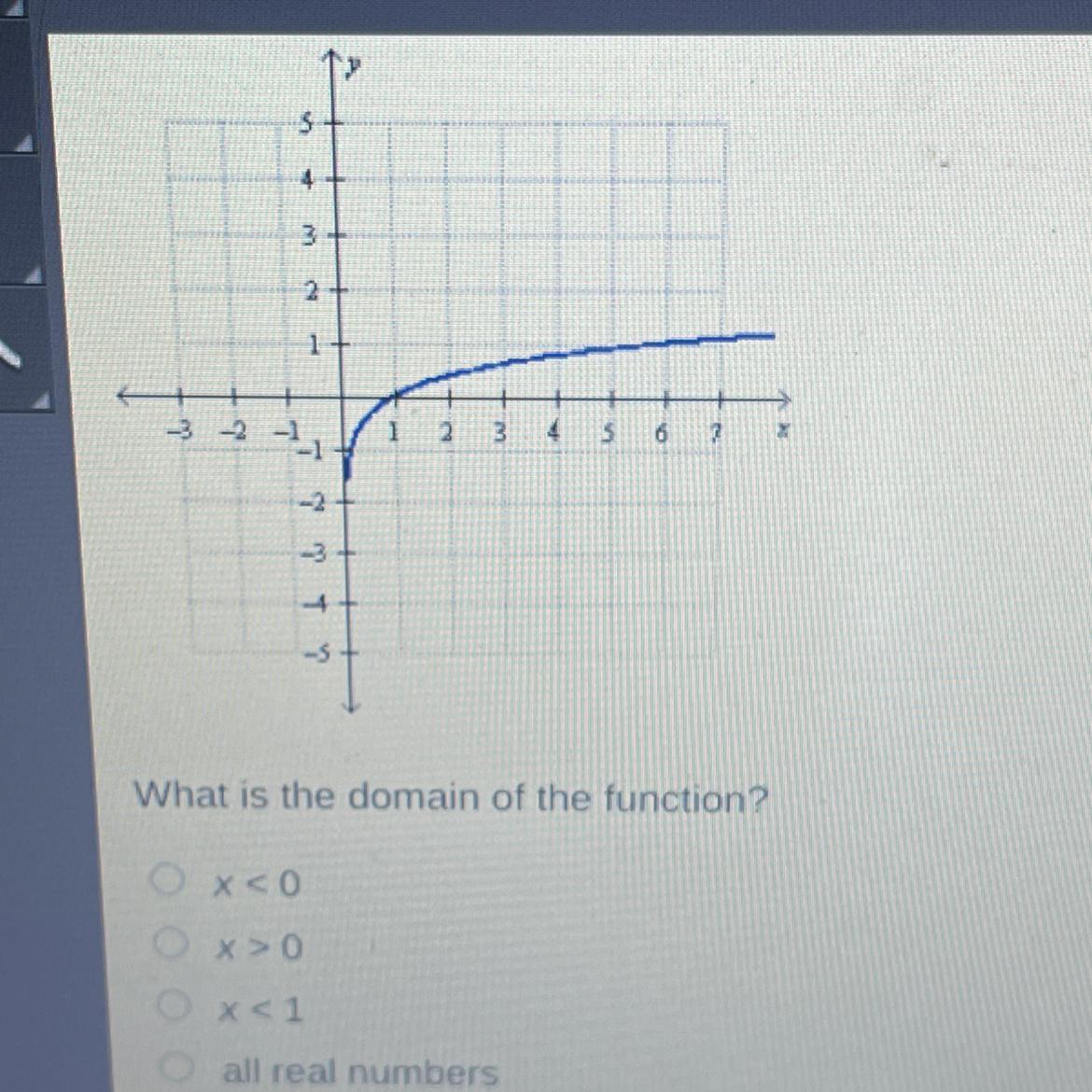
What is the domain of the function?
x<0
X>0
O x < 1
all real numbers
Answers
Answer:
\(x > 0\)
Step-by-step explanation:
The x-values (domain/input) are greater than 0
In other words, the graph covers the x-axis on all points greater than 0
Answer: the function is defined for all real values of x. Therefore, the domain of the function is the set of all real numbers, which can be denoted as:
Domain = (-∞, ∞) or (-∞, +∞)
On Melissa's 6th birthday, she gets a $4000 CD that earns 6% interest, compounded quarterly. If the CD
matures on her 16th birthday, how much money will be available?
Answers
Answer:
On melissa's 6th birthday, she gets a $4000 cd that earns 3% interest, compounded quarterly. If... | like | dislike ... The amount accumulated in a certificate of deposit (CD) is found using the compound interest formula as a CD also earns compounding interest. ... The number of years between the 6th and 12th birthdays is 6
Step-by-step explanation:
There will be $41142.87 available on Melissa's 16th birthday.
What is compound interest?Interest accrued on both the principal sum of money and the interest already earned.
The formula for compound interest is p(1+r/100)ⁿ - p
Where p is principal, r is rate and n is time.
Given that,
Amount that Melissa gets on her 6th birthday = $4000
Rate of interest = 6% compounded quarterly.
Melissa gets amount on her 16th birthday, time = 6 years
The amount that Melissa will get on her 16th birthday
= 4000(1+6/100)¹⁰ˣ⁴
= 4000 (106/100)⁴⁰
= 4000 x 10.2857
= 41142.87
Melissa will get $41142.87 on her 16th birthday.
To know more about Compound interest on:
https://brainly.com/question/22621039
#SPJ2
Find an equation for the nth term of the arithmetic sequence. 9, 11, 13, 15, ...
Answers
Answer:
2n+7
Step-by-step explanation:
First lets find the common difference which is 2, now we can use this formula to find the nth term.
an = a1 + (n - 1 ) d
an= 9+(n-1)2
=9+2n-2
=2n+7
To check let's insert n=5, 2(5)=10+7=17.
15+2=17!
(1) (1 pt. Find the volume trapped below the cone z = V x2 + y2 = r over the semicircular disk: 2.0 y 7 1.5 + r dr do 1.0 r: 0 ??? 0.5 0: 0 + 7/2 ...
Answers
The volume trapped below the cone and over the semicircular disk can be calculated using the given equation z = Vx^2 + y^2 = r. The integral to evaluate the volume is ∫∫(0 to 1)(0 to 0.5 + √(7/2 - r^2))(r dr do).
To find the volume, we first need to understand the geometry of the problem. The equation z = Vx^2 + y^2 = r represents a cone with its vertex at the origin and its axis along the z-axis. The parameter V determines the slope of the cone, while r represents the radial distance from the origin. The semicircular disk lies in the xy-plane and is defined by the inequality 0 ≤ r ≤ 0.5 and 0 ≤ θ ≤ π.
To calculate the volume, we need to express the volume element in terms of the cylindrical coordinates r, θ, and z. In cylindrical coordinates, the volume element is given by dV = r dr do dz. However, in this case, since we are integrating over a semicircular disk, the range of θ is limited to π. Thus, the volume element becomes dV = r dr do dz, where r ranges from 0 to 0.5, θ ranges from 0 to π, and dz ranges from 0 to 0.5 + √(7/2 - r^2).
Now, we can set up the integral to evaluate the volume trapped below the cone and over the semicircular disk. The integral becomes ∫∫∫(0 to 1)(0 to π)(0 to 0.5 + √(7/2 - r^2))(r dr do dz). Evaluating this integral will give us the desired volume.
In conclusion, the volume trapped below the cone z = Vx^2 + y^2 = r over the semicircular disk is given by the integral ∫∫∫(0 to 1)(0 to π)(0 to 0.5 + √(7/2 - r^2))(r dr do dz), where V is the slope of the cone and r ranges from 0 to 0.5.
Learn more about volume here
https://brainly.com/question/27710307
#SPJ11
a function f(z)=u(x,y) iv(x,y) is analytic on a set g answer if the first partial derivatives of u and v satisfy the cauchy-riemann equations on g.
Answers
A function f(z) = u(x, y) + iv(x, y) is considered analytic on a set G if the first partial derivatives of u and v satisfy the Cauchy-Riemann equations on G.
The Cauchy-Riemann equations are given by:
1. ∂u/∂x = ∂v/∂y
2. ∂u/∂y = -∂v/∂x
To determine if the function is analytic on G, follow these steps:
1. Calculate the first partial derivatives of u with respect to x and y, denoted as ∂u/∂x and ∂u/∂y.
2. Calculate the first partial derivatives of v with respect to x and y, denoted as ∂v/∂x and ∂v/∂y.
3. Check if the calculated partial derivatives satisfy the Cauchy-Riemann equations mentioned above.
4. If both equations are satisfied, the function f(z) is analytic on the set G.
To learn more about “function” refer to the https://brainly.com/question/2328150
#SPJ11
A triangle has two sides of length 1 and 4. What is the largest possible whole-number length
for the third side?
Answers
Using the triangle inequality theorem, the largest possible whole-number length for the third side is 4.
How to Apply the Triangle Inequality Theorem to Find the Length of the Third Side of a Triangle?The third side of a triangle must be shorter than the sum of the other two sides and longer than the difference between the other two sides.
So, for a triangle with sides of length 1, 4, and x (where x is the length of the third side), we have:
1 + 4 > x
4 + x > 1
1 + x > 4
Simplifying these inequalities, we get:
5 > x
x > 3
x > -3 (this inequality is always true)
The largest possible whole-number length for the third side is 4, since it is the largest integer that satisfies the above inequalities.
Learn more about the triangle inequality theorem on:
https://brainly.com/question/309896
#SPJ1
Answer questions 8,9 and 10
If the resistance voltage is given by 200 \( \cos (t) \), then Vout after 5 minutes is: (0/2 Points) \( 173.2 \) volt 200 volt \( 6.98 \) volt 343.6 Volt None of them
Answers
the correct answer is: Vout after 5 minutes is approximately -173.2 volts.
To find the value of Vout after 5 minutes when the resistance voltage is given by 200 \( \cos (t) \), we need to evaluate the expression 200 \( \cos (t) \) at t = 5 minutes.
Given that 1 minute is equal to 60 seconds, 5 minutes is equal to \( 5 \times 60 = 300 \) seconds.
So, we need to calculate 200 \( \cos (300) \).
Evaluating this expression using a calculator, we find:
200 \( \cos (300) \approx -173.2 \) volts.
Therefore, the correct answer is:
Vout after 5 minutes is approximately -173.2 volts.
Please note that the negative sign indicates a phase shift in the cosine function, which is common in AC circuits.
to learn more about Vout.
https://brainly.com/question/30481853
#SPJ11
2. How many bits are needed to represent decimal values ranging from 0 to 12,500?
Answers
To represent decimal values ranging from 0 to 12,500, we need 14 bits.
To determine the number of bits needed to represent decimal values ranging from 0 to 12,500, we need to find the smallest number of bits that can represent the largest value in this range, which is 12,500.
The binary representation of a decimal number requires log base 2 of the decimal number of bits. In this case, we can calculate log base 2 of 12,500 to find the minimum number of bits needed.
log2(12,500) ≈ 13.60
Since we can't have a fraction of a bit, we round up to the nearest whole number. Therefore, we need at least 14 bits to represent values ranging from 0 to 12,500.
Using 14 bits, we can represent decimal values from 0 to (2^14 - 1), which is 0 to 16,383. This range covers the values 0 to 12,500, fulfilling the requirement.
Learn more about whole number
brainly.com/question/29766862
#SPJ11
Elise says, "If you subtract 18 from my number and multiply the difference by - 3, the result is
- 33." What is Elise's number?
Answers
Elise's number is 29.
If you think of multiplying a value by -3 to get -33, it would obviously be 11.
So in this case, you would want to add 18 to 11 to get Elise's number, which is 29. Subtracting 18 from 29 would get you back to the value of 11, which you can then multiply it by -3 again to get -33.
7th grade math help me plzzz
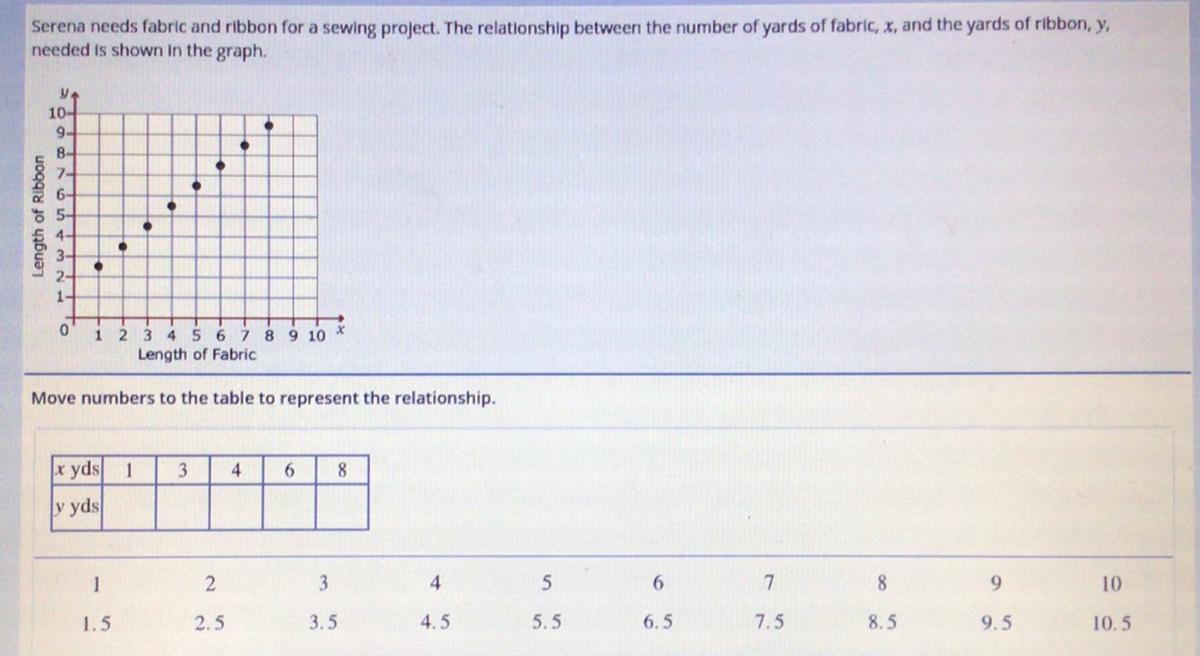
Answers
Answer:
1,2.5
3,4.5
4,5.5
6,7.5
8,9.5
Step-by-step explanation:
Help me pleaseeeeee!!!
Anyone???

Answers
Answer:
Sorry if this is wrong I haven't done this in like a year or two but it should be B.
Step-by-step explanation:
Would take seven years to type out and not sure if I even did the math right
Prizes and the chances of winning in a sweepstakes are given in the table below.
Prize Chances
$10,000,000 1 chance in 300,000,000
$350,000 1 chance in 150,000,000
$50,000 1 chance in 10,000,000
$20,000 1 chance in 1,000,000
$400 1 chance in 200,000
A watch valued at $75 1 chance in 6,000
(a) Find the expected value (in dollars) of the amount won by one entry.
(b) Find the expected value (in dollars) if the cost of entering this sweepstakes is the cost of a postage stamp (34 cents)
Answers
The expected value of the discrete distribution, for each case, is given as follows:
a) Amount won by one entry: $0.075.
b) If the cost is the cost of a postage stamp: -$0.525.
How to obtain the expected value of a discrete distribution?The expected value of a discrete distribution is obtained with the sum of each outcome multiplied by it's probabillity.
In this problem, the distribution for the prizes is given as follows:
P(X = 10,000,000) = 1/300,000,000.P(X = 350,000) = 1/150,000,000.P(X = 50,000) = 1/10,000,000.P(X = 20,000) = 1/1,000,000.P(X = 400) = 1/200,000.P(X = 75) = 1/6,000.Hence the expected value for the prizes is:
E(X) = 10,000,000 x 1/300,000,000 + 350,000 x 1/150,000,000 + 50,000 x 1/10,000,000 + 20,000 x 1/1,000,000 + 400 x 1/200,000 + 75 x 1/6,000 = $0.075.
The cost of a postage stamp is of $0.6, hence the expected value considering this cost would be of:
0.075 - 0.6 = -$0.525.
More can be learned about the expected value of a discrete distribution at https://brainly.com/question/27899440
#SPJ1
HELP!!! NEED ANSWER FAST

Answers
Answer:
y = 1.3x + 10
Step-by-step explanation:
as, y = 1.3 * 5 + 10
= 16.5
Answer: y = 1.3x + 10
Step-by-step explanation: 1.3 x 0 = 0→ 0 + 10 = 10
1.3 x 5 = 6.5→ 6.5 + 10 = 16.5
1.3 x 10 = 13→ 13 + 10 = 23
1.3 x 15 = 19.5→ 19.5 + 10 = 29.5
1.3 x 20 = 26→ 26 + 10 = 36
Hope this helps.
$5 is what percent of $10?
Answers
Answer:
It was 50%
Step-by-step explanation:
Name the property of real numbers illustrated by each equation.
-10+4 = 4+(-10)
Answers
The property of real numbers illustrated by the equation -10+4 = 4+(-10) is the commutative property of addition. This property states that changing the order of the numbers being added does not change the sum.
In this equation, both sides are equal because the order of the numbers being added is changed, but the sum remains the same. Therefore, the commutative property of addition is being illustrated.The property of real numbers illustrated by the equation:
-10 + 4 = 4 + (-10)
is the Commutative Property of Addition.
The Commutative Property of Addition states that the order of the numbers being added does not affect the sum. In other words, when adding two real numbers, changing the order of the numbers being added does not change the result.
In the given equation, both sides of the equation have the same sum (-6), even though the order of the terms has been reversed. This demonstrates the Commutative Property of Addition.
To know more about real numbers, visit:
https://brainly.com/question/17201233
#SPJ11
for the linear equation y = 2x 4, if x increases by 1 point, how much will y increase? (hint: think about the definition of the slope) group of answer choices 2 points 3 points 1 points 4 points
Answers
For the linear equation y = 2x 4, if x increases by 1 pointThe value of y will increase by 2 points(A).
The equation y = 2x + 4 represents a linear relationship, where the coefficient of x, which is 2, represents the slope of the line. The slope indicates how much y changes when x increases by 1. In this case, the slope is 2, meaning that for every increase of 1 in x, y will increase by 2.
Therefore, For the linear equation y = 2x 4, if x increases by 1 point,the value of y will increase by 2 points(A). This means that correct option is A.
For more questions like Equation click the link below:
https://brainly.com/question/16663279
#SPJ11
Regenerate response
CORE
SKILL
ADVANCED
If a is inversely related to the square of b, and a = 3 when bis
8, which of the following is another possible value for a and b?
(A) a = 4, b = 12
(B) a = 12, b = 4
(C) a = 8, b = 3
(D) a = 2, b = 4
(E) a = 6, b = 4
Answers
Another possible values for a and b are a = 12 and b = 4
How to find another possible value for a and b?
A variation is a relation between a set of values of one variable and a set of values of other variables
Given that: a is inversely related to the square of b, and a = 3 when bis
8.
This can be written as:
a α 1/b²
a = k/b² (where k is a constant)
k = ab²
since a = 3 and b = 8.
Thus, k = 3 × 8² = 3 × 64 = 192
For a value to be another possible value for a and b, they must give k = 192 when substituted into the equation k = ab²:
a = 4, b = 12: k = 4 × 12² = 576
a = 12, b = 4: k = 12 × 4² = 192
a = 8, b = 3: k = 8 × 3² = 72
a = 2, b = 4: k = 2 × 4² = 32
a = 6, b = 4: k = 6 × 4² = 96
The values that produce k = 192 are a = 12 and b = 4. Therefore, another possible value for a and b is a = 12 and b = 4. So option B is the answer
Learn more about variation on:
https://brainly.com/question/2375770
#SPJ1
Suppose the time spent by a randomly selected student who use a terminal connected to a local time -sharing computer facility has a gamma distribution with mean 20 min and variance 80 min^2.values of alpha and beta?b. probability that a student uses the terminal for at most 24min?c. probability that a student spends between 20 and 40min useing the terminal?
Answers
a) The values of alpha and beta are: α = 4, β = 5
b) The probability that a student uses the terminal for at most 24 min = 0.7149
c) The probability that a student spends between 20 and 40min useing the terminal = 0.3911
We know that the theorem: The limiting distribution of the gamma(α, β) distribution is the N(μ, σ²) distribution where μ = αβ and σ² = αβ²
Here, mean (μ) = 20 min and variance (σ²) = 80 min²
After solving these equation for α and β we get,
α = 80/20
α = 4
and β = 20/4
β = 5
The formula for the gamma distribution is shown in attached image.
And the formula for the gamma function is Γ(α) = ∫_{0-∞} (\(y^{\alpha -1}e^t\))dy
The probability that a student uses the terminal for at most 24 min:
P(X ≤ 24) = F(24; α, β)
= F(24/α , β)
= F(6, 5)
= 0.7149 ............(Using the gamma distribution formula)
The probability that a student spends between 20 and 40min using the terminal.
= P(X ≥ 20) - P(X ≥ 40)
= F(20/α , β) - F(40/α , β)
= F(5, 5) - F(10, 5)
= 0.43347 - 0.04238 ............(Using the gamma distribution formula)
= 0.3911
Learn more about the probability here:
https://brainly.com/question/15124899
#SPJ4

1. take away five from twelve times f. 2. one-half of the sum of k and six 3.x squared minus the sum of 5 4.the sum of the product of a and b, and three times c 5.twenty-four times the product of x and y, plus g.
Answers
The expressions formed are,
12f -5(k+6)/2x²-x+5ab+3c24xy+gFormation of expressions in 1, 2 and 3:
In 1, twelve times f is, 12f
Taking away 5, it becomes (12f-5)
In 2, sum of k and 6 is, (k+6)
One-half of the above quantity is, (k+6)/2
In 3, sum of 5 with x is, (x+5)
Now, x squared minus the above expression indicates (x²-x+5)
Formation of expressions in 4 and 5:
In 4, product of a and b, is ab and 3 times c is 3c
Sum of the expressions evaluated in the previous statement = ab+3c
In 5, 24 times the product of x and y is, 24xy
Adding, g in the above computed expression, we get, 24xy+g
Learn more about expressions here:
https://brainly.com/question/17167810
#SPJ4
what is the value of r of the geometric series?
Answers
Value of r is different for every series
let
a , b , c , d ..... be geometric series then
r = b/a or d/c and so on
where r is common ratio
A company had returns of 5%, 10%, -15%, 20%, -12%, 22%, 8% in
the last few years. Compute the arithmetic average return,
geometric average return, variance, and standard deviation of
returns.
Refer to
Answers
Arithmetic average return of the company is 2.57%.Geometric average return of the company is 13%.Variance of the company is 56.Standard deviation of the company is 7.48%.
Given, Returns of the company for the last few years are 5%, 10%, -15%, 20%, -12%, 22%, 8%
Arithmetic Average return:
Arithmetic Average return = (sum of all returns) / (total number of returns)
Arithmetic Average return = (5 + 10 - 15 + 20 - 12 + 22 + 8) / 7= 18 / 7= 2.57
Therefore, the arithmetic average return of the company is 2.57%.
Geometric average return:
Geometric average return = [(1+R1) * (1+R2) * (1+R3) * …….. * (1+Rn)]1/n - 1
Geometric average return = [(1.05) * (1.1) * (0.85) * (1.2) * (0.88) * (1.22) * (1.08)]1/7 - 1= 0.13
Therefore, the geometric average return of the company is 13%.
Variance:
Variance = (sum of (return - mean return)2) / (total number of returns)
Mean return = (5 + 10 - 15 + 20 - 12 + 22 + 8) / 7= 18 / 7= 2.57
Variance = [(5-2.57)2 + (10-2.57)2 + (-15-2.57)2 + (20-2.57)2 + (-12-2.57)2 + (22-2.57)2 + (8-2.57)2] / 7= 392.12 / 7= 56
Therefore, the variance of the company is 56.
Standard Deviation:
Standard Deviation = Square root of Variance
Standard Deviation = √56= 7.48
Therefore, the standard deviation of the company is 7.48%.
Thus, Arithmetic average return of the company is 2.57%.Geometric average return of the company is 13%.Variance of the company is 56.Standard deviation of the company is 7.48%.
To know more about arithmetic average return, click here
https://brainly.com/question/28562900
#SPJ11
Find the measures of the angles between the diagonals of the rectangle whose vertices are a = (1, 0), b = (0, 3), c = (3, 4), and d = (4, 1)
Answers
Answer:
The angle between the diagonal of the rectangle is \(\frac{\pi }{2}\).
Given:
The vertices of the rectangle are
a = (1, 0), b = (0, 3), c = (3, 4), and d = (4, 1)
To find:
The objective is to find the angle between the diagonals.
Step 1 of 3
Consider the diagram attached.
Step 2 of3
The position vector of diagonal AC is-
=(3-1)î+(4-0)j=2î+4j
And the position vector of diagonal BD is-
=(4-0)î+(1-3)j=4î-2j
Step 3 of 3
cosθ=\(\frac{AC.BD}{|AC|.|BD|}\)
cosθ=\(\frac{(2i-4j)(4i-2j)}{\sqrt{2^2+4^2} \sqrt{4^2+(-2)^2\\} }\)
=\(\frac{8-8}{\sqrt{20}.\sqrt{20} }\)
=0
θ=\(cos^{-1}\)(0)
θ=\(\frac{\pi }{2}\)
Therefore the angle between the diagonal of the rectangle is \(\frac{\pi }{2}\)
https://brainly.com/question/25705666
#SPJ4

The angle between the diagonals of a rectangle is π/2
A rectangle is a parallelogram, so opposite sides are equal. The diagonals of rectangle are equal and bisect each other at 90°. A diagonal of a rectangle is a line segment that connects two non-adjacent vertices.A diagonal divides the rectangle in 2 right triangles. where the sides are equal to the sides and the hypotenuse of the rectangle.
The vertices of the rectangle are
a = (1, 0), b = (0, 3), c = (3, 4), d = (4, 1)
The diagonal position vector AC
=(3-1)î+(4-0)j=2î+4j
And the diagonal position vector BD
=(4-0)î+(1-3)j=4î-2j
cos Ф = (AC.BD) / (|AC| . |BD|)
cos Ф = (8-8) / (root20 -roo20)
= 0
Ф = π/2
Therefore the angle between the diagonals of the rectangle is π/2
Learn more about diagonals here
https://brainly.com/question/26154016
#SPJ4
