Four students are getting ready for a running competition. They each set a goal to run
a certain number of laps in the week before the competition.

Ivory's goal is to run 50
laps. They ran 35 laps. What percent of their goal is this?

Answer:

\(\displaystyle \frac{dh}{dt}=-\frac{4}{\pi}\approx-1.2732\text{ centimeters per minute}\)

The water level is dropping by approximately 1.27 centimeters per minute.

Step-by-step explanation:

Please refer to the attached diagram.

The height of the conical container is 6 cm, and its radius is 1 cm.

The container is leaking water at a rate of 1 cubic centimeter per minute.

And we want to find the rate at which the water level h is dropping when the water height is 3 cm.

Since we are relating the water leaked to the height of the water level, we will consider the volume formula for a cone, given by:

\(\displaystyle V=\frac{1}{3}\pi r^2h\)

Now, we can establish the relationship between the radius r and the height h. At any given point, we will have two similar triangles as shown below. Therefore, we can write:

\(\displaystyle \frac{1}{6}=\frac{r}{h}\)

Solving for r yields:

\(\displaystyle r=\frac{1}{6}h\)

So, we will substitute this into our volume formula. This yields:

\(\displaystyle \begin{aligned} V&=\frac{1}{3}\pi \Big(\frac{1}{6}h\Big)^2h\\ &=\frac{1}{108}\pi h^3\end{aligned}\)

Now, we will differentiate both sides with respect to time t. Hence:

\(\displaystyle \frac{d}{dt}[V]=\frac{d}{dt}\Big[\frac{1}{108}\pi h^3\Big]\)

The left is simply dV/dt. We can move the coefficient from the right:

\(\displaystyle \frac{dV}{dt}=\frac{1}{108}\pi\frac{d}{dt}\big[h^3\big]\)

Implicitly differentiate:

\(\displaystyle\begin{aligned} \frac{dV}{dt}&=\frac{1}{108}\pi(3h^2\frac{dh}{dt})\\ &=\frac{1}{36}\pi h^2\frac{dh}{dt}\end{aligned}\)

Since the water is leaking at a rate of 1 cubic centimeter per minute, dV/dt=-1.

We want to find the rate at which the water level h is dropping when the height of the water is 3 cm.. So, we want to find dh/dt when h=3.

So, by substitution, we acquire:

\(\displaystyle -1=\frac{1}{36}\pi(3)^2\frac{dh}{dt}\)

Therefore:

\(\displaystyle -1=\frac{1}{4}\pi\frac{dh}{dt}\)

Hence:

\(\displaystyle \frac{dh}{dt}=-\frac{4}{\pi}\approx-1.2732\text{ centimeters per minute}\)

The water level is dropping at a rate of approximately 1.27 centimeters per minute.

Answer:

congruent and parallel those are two of them i dont know the other 2 sorry

Step-by-step explanation:

Answer: 3/4 of the original price.

Step-by-step explanation:

Ok, so Sam buys 4 boxes in Store A.

We know that in Store A you can get 4 boxes paying only for 3.

If P is the price of a Box, then he got 4 boxes and paid 3*P

then the amount that he paid for each box is equal to the total amount that he paid divided the number of boxes that he received.

this is: 3P/4 = (3/4)*P

Meaning that he paid 3/4 of the original price for each box.

The given series is convergent and the sum(S) is 5.555.

Consider 10 - 8 + 6.4 - 5.12 + ...

A geometric progression will converge if the common ratio of the series is between -1 and 1.

Here is the common ratio,

r = -8/10

⇒ r = -0.8

Which is -1 < -0.8 < 1.

Hence, the given series is convergent.

Sum of series = S = a/(1 - r)

Here, first term(a) = 10,

common ratio(r) = -0.8,

S = a/(1 - r)

⇒ S = 10/(1 - (-0.8))

⇒ S = 10/(1 + 0.8)

⇒ S = 10/1.8

⇒ S = 5.555

Therefore, the given series is convergent and the sum( S)is 5.555.

Read more about geometric progression :

https://brainly.com/question/12006112

#SPJ4

Using the length formula we know that the length of the given arc is 30.144 miles.

In mathematics, an arc is a portion of the boundary of a circle or curve. It is sometimes referred to as an open curve.

The measurement around a circle that determines its edge is called the circumference, often known as the perimeter.

So, the formula to find the length of the arc is:

Length of an Arc = θ × r

Now, insert values and calculate as follows:

Length of an Arc = θ × r

Length of an Arc = 4π/5 × 12

Length of an Arc = 4π/5 × 12

Length of an Arc = 12.56/5 * 12

Length of an Arc = 2.512 * 12

Length of an Arc =  30.144

Therefore, using the length formula we know that the length of the given arc is 30.144 miles.

Know more about an arc here:

https://brainly.com/question/2005046

#SPJ1

Answer:

A: x = AllRealNumbers

B: The solution is all real numbers except x = 2

Step-by-step explanation:

Part A:

(x^2 - 7x - 18)/(x + 2) = x - 9

(x - 9)(x + 2)/(x + 2) = x - 9

x - 9 = x - 9

x = AllRealNumbers

Part B:

Since the denominator is (x + 2), the only solution that will cause the equation to be undefined is x = 2.

Answer:

A: x = all real numbers

B: the solution is all real numbers except x = 2

Step-by-step explanation:

hope it helps

Answer:

Third graph is the correct choice. See below.

Step-by-step explanation:

See the attachment below.

Best Regards!

Answer: 6

Step-by-step explanation: Solution: Perimeter of the triangle is the sum of the lengths of its sides. Thus, perimeter = 10 cm. 6.

Answer:

i believe i have to multiply and i got 4 4/5

so 4 FULL servings and 4/5 cereal servings left over

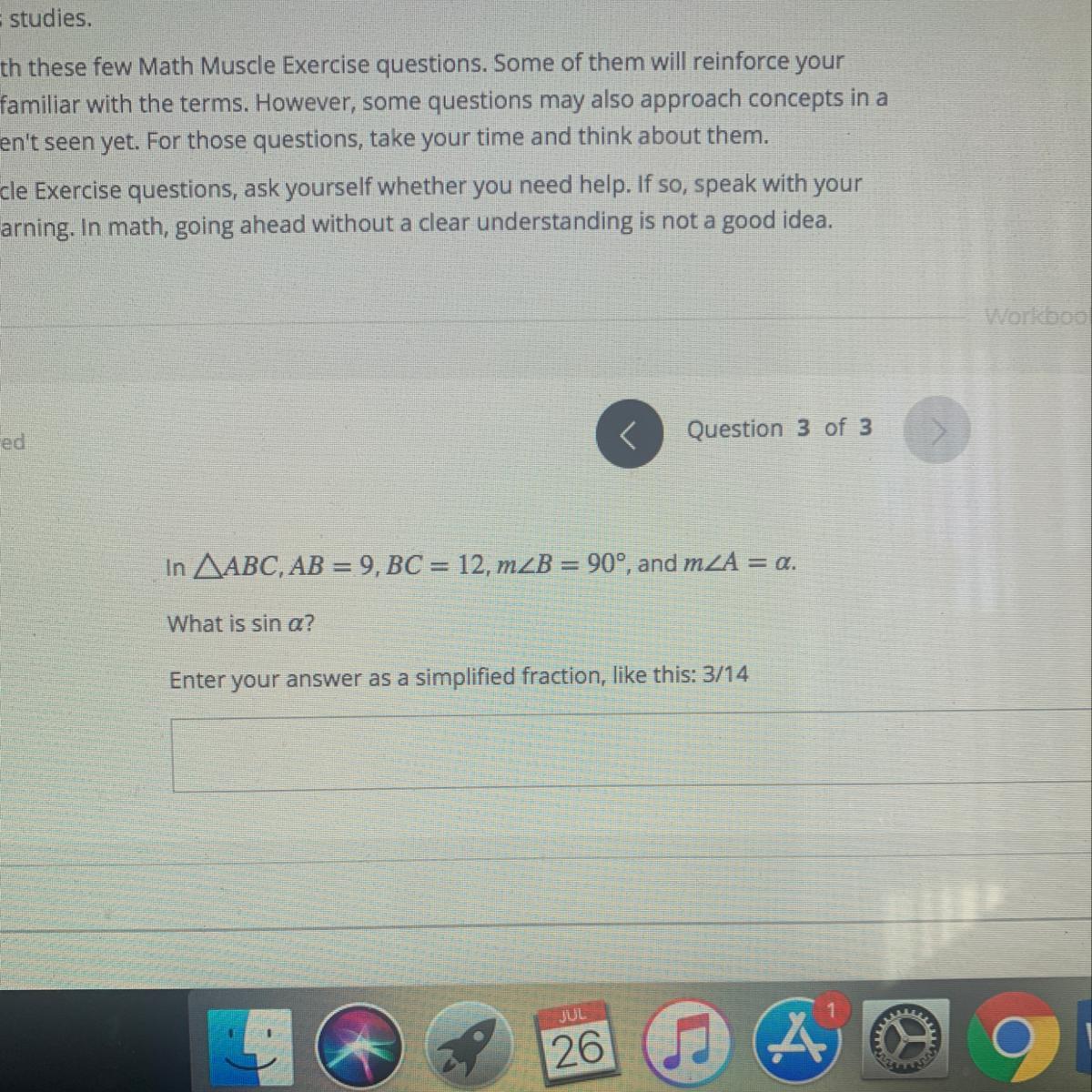
Answers:

sin a=12/15=4/5

step by step explanation:

AB=9, and BC=12

find c: hyp.=√12²+9²=c²

c=15

sin a=opp/hyp.=12/15=4/5 ( convert to degrees)

a=41.10

Answer:

\(\boxed{\sf \boxed{\sf n=\frac{11}{4}}\; or\;\boxed{\sf n=2.75}}\)

Step-by-step explanation:

\(\sf 3n + 2 + 5n = 24\)

Combine like terms:-

\(\sf 3n+5n+2=24\)

\(\sf 3n+5n=\bf 8n\)

\(\sf 8n+2=24\)

Subtract both sides by 2:-

\(\sf 8n+2-2=24-2\)

Simplify:-

\(\sf 8n=22\)

Divide both sides by 8:-

\(\sf \cfrac{8n}{8}=\cfrac{22}{8}\)

\(\sf n=\cfrac{11}{4}\)

___________________

Hope this helps!

Have a great day!

Answer:

n = 11/4

Step-by-step explanation:

Given equation,

→ 3n + 2 + 5n = 24

Now the value of n will be,

→ 3n + 2 + 5n = 24

→ 3n + 5n = 24 - 2

→ 8n = 22

→ n = 22/8

→ [ n = 11/4 ]

Hence, value of n is 11/4.

Answer:

First, evaluate 3^3

3^3 means three times itself three times.

\(3 * 3 * 3 = 27\)

\(\sqrt{27} = 5.19\)

Next, square root eight.

\(\sqrt{8} = 2.82\)

Now, divide the two numbers.

\(5.19 / 2.82 = 1.84\) if needed, include full form: 1.840425531914894

(3n)³ = 27

= 27√8 = 2.82

= 27√8 = 2.82√27 = 5.19

5.19/2.82 = 1.84

Here is your answer buddy..

Answer:

(0, 2)

Step-by-step explanation:

Answer:

A. {All Integers}, because it will go on forever

The value of the number is x = 34.

Let's break down the problem and solve it step by step.

1. "Five less than twice the value of a number": This can be represented as 2x - 5, where x is the number.

2. "Three times the quantity of 4 more than 1/2 the number": This can be represented as 3 * (x/2 + 4).

According to the problem statement, the two expressions are equal. We can set up the equation as follows:

2x - 5 = 3 * (x/2 + 4)

Now, let's solve the equation:

2x - 5 = 3 * (x/2 + 4)

Distribute the 3 to both terms inside the parentheses:

2x - 5 = (3/2)x + 12

Multiply through by 2 to eliminate the fraction:

2(2x - 5) = 2((3/2)x + 12)

4x - 10 = 3x + 24

Next, let's isolate the x term by moving the constant terms to the other side of the equation:

4x - 3x = 24 + 10

Simplify:

x = 34

For more such questions on number,click on

https://brainly.com/question/24644930

#SPJ8

\( \bf \underline{Given :-}\)

\( \\ \\ \)

\( \bf \underline{ To \: find:-}\)

\( \\ \\ \)

\( \bf \underline{Solution:-}\)

Strongly recommend to keep up with Digram , as name of sides are based according to Digram.

As we know soccer feild is rectangle , therefore ∠A = ∠B = ∠C = ∠D = 90°

Now as we have to just find value of diagonal AD therefore just focus on triangle ACD.

we know ∠C = 90° , triangle ACD. is a right angled triangle.

\( \\ \\ \)

\( \bigstar \boxed{ \rm Hypotenuse^2 = Base^2 + Perpendicular^2}\)

Here :-

Hypotenuse = AD

Base = CD

Perpendicular = AC

\( \\ \)

Therefore :-

\( \\ \)

\( \dashrightarrow\sf AD^2 =CD^2 + AC^2 \\ \)

\( \\ \\ \)

\( \dashrightarrow\sf AD^2 =(130)^2 + (80)^2 \\ \)

\( \\ \\ \)

\( \dashrightarrow\sf AD^2 =130 \times 130 + (80)^2 \\ \)

\( \\ \\ \)

\( \dashrightarrow\sf AD^2 =16900+ (80)^2 \\ \)

\( \\ \\ \)

\( \dashrightarrow\sf AD^2 =16900+80 \times 80 \\ \)

\( \\ \\ \)

\( \dashrightarrow\sf AD^2 =16900+6400\\ \)

\( \\ \\ \)

\( \dashrightarrow\sf AD^2 =23300\\ \)

\( \\ \\ \)

\( \dashrightarrow\sf AD= \sqrt{23300} \\ \)

\( \\ \\ \)

\( \dashrightarrow\bf AD =152.643 \: yds\\ \)

\( \\ \\ \)

By solving a system of equations, we will see that the scientist needs to use:

First, we need to define the variables, we will use:

We know that the scientist needs 5.4 liters, then we will have that:

x + y = 5.4

We also know that the end concentration for these 5.4 liters must be 28%, then the concentration in the left side must be the same as the one in the right side, this gives the equation:

0.12*x + 0.30*y = 0.28*(5.4)

0.12*x + 0.30*y = 1.512

Then the system of equations is:

x + y = 5.4

0.12*x + 0.30*y = 1.512

To solve it, we first need to isolate one of the variables in one of the equations, I will isolate x in the first one.

x = 5.4 - y

Now we can replace this in the other equation to get:

0.12*(5.4 - y) + 0.30*y = 1.512

0.81 - 0.12*y + 0.30*y = 1.512

(0.30 - 0.12)*y = 1.512 - 0.81

0.18*y = 0.712

y = (0.712)/0.18 = 3.956

And to find the value of x, we use:

x = 5.4 - y = 5.4 - 3.956 = 1.444

So the scientist needs to use:

If you want to learn more about systems of equations, you can read:

https://brainly.com/question/13729904

Answer:

3.25r

Step-by-step explanation:

Im converting them to decimals because its easier to write on brainly so 0.75r+2r+0.5r = 3.25r

Answer:

Answer is 11r/4 + 1/2

Step-by-step explanation:

3/4r + 2r + 1/2 = 11r/4 + 1/2

When a transversal cuts through a pair of parallel lines, it creates pairs of angles with special properties.

The complete proof is:

From the question, we have the following given parameter

\(\mathbf{\angle 2\ and\ \angle 5}\) are supplementary angles

So, the first blanks are:

Next, we have:

\(\mathbf{\angle 3 \cong \angle 2}\)

This is because both angles are vertical angles

So, the second blank is: vertical angle theorem.

Also,

Angles 3 and 5 are supplementary angles because they add up to 180 degrees, and they are both at the same interior side of the transversal.

So, the third blank is Same side interior angle.

The above highlights mean that \(\mathbf{l \ ||\ m}\) has been proved.

So, the last blanks are:

Read more about two-column proofs at:

https://brainly.com/question/9198561

The dude above me is 100% correct

The percentage of buyers is approximately 68.26% of buyers of new houses paid between \($149,000\) and \($151,000\) .

We are given that the prices of the new homes are normally distributed with a mean of \($150,000\) and a standard deviation of $1000.

Using the 68-95-99.7 rule, we know that: approximately 68% of the data falls within one standard deviation of the mean approximately 95% of the data falls within two standard deviations of the mean, approximately 99.7% of the data falls within three standard deviations of the mean.

In order to determine the proportion of customers who spent between $149,000 and , we must first determine the z-scores for these values:

z1 = (149,000 - 150,000) / 1000 = -1 z2 = (151,000 - 150,000) / 1000 = 1

Now, we can determine the proportion of data that falls between z1 and z2 using the z-table or a calculator. The region to the left of z1 is 0.1587, and the area to the left of z2 is 0.8413, according to the z-table. Thus, the region bounded by z1 and z2 is:

0.8413 - 0.1587 = 0.6826

We can get the percentage of consumers who spent between by multiplying this by 100% is  \($149,000\)  and \($151,000\):

0.6826 x 100% = 68.26%

Therefore, the standard deviation of customers who paid between is \($149,000\) and \($151,000\)  for this model of new homes.

For such more questions on standard deviation

https://brainly.com/question/30557671

#SPJ11

Answer:

(a) Always true

Step-by-step explanation:

In the case when there is a matrix of coefficient for a homogeneous system for n linear equations so it does not have an opposite and then the system would be have the infinite various solutions

So this is always true as in this it can be unique test or infinite.

So according to the given situation, the option a is correct

The dividends per share for preferred stock for each year are: Year 1 - $1.25, Year 2 - $2.25, Year 3 - $3.25. The dividends per share for common stock for each year are all $0.

To determine the dividends per share for preferred and common stock for each year, we need to divide the total dividends by the number of shares for each type of stock.

Preferred Stock:

Dividends per share of preferred stock = Total dividends for preferred stock / Number of preferred shares

Year 1:

Dividends per share of preferred stock for Year 1 = $50,000 / 40,000 shares = $1.25

Year 2:

Dividends per share of preferred stock for Year 2 = $90,000 / 40,000 shares = $2.25

Year 3:

Dividends per share of preferred stock for Year 3 = $130,000 / 40,000 shares = $3.25

Common Stock:

Dividends per share of common stock = Total dividends for common stock / Number of common shares

Year 1:

Dividends per share of common stock for Year 1 = ($50,000 - Total dividends for preferred stock) / 100,000 shares = ($50,000 - $50,000) / 100,000 shares = $0

Year 2:

Dividends per share of common stock for Year 2 = ($90,000 - Total dividends for preferred stock) / 100,000 shares = ($90,000 - $90,000) / 100,000 shares = $0

Year 3:

Dividends per share of common stock for Year 3 = ($130,000 - Total dividends for preferred stock) / 100,000 shares = ($130,000 - $130,000) / 100,000 shares = $0

The dividends per share for preferred stock for each year are: Year 1 - $1.25, Year 2 - $2.25, Year 3 - $3.25. The dividends per share for common stock for each year are all $0.

for more questions on stock

https://brainly.com/question/18124452

#SPJ8

Answer: is A

Step-by-step explanation:

Answer:

f(3) = 1728

f(-2) = 1/144

f(1/2) = 2sqrt(3)

Step-by-step explanation: all you is replace x with what ever is in the parenthesis

The year 1 housing cost  is $15,009.00, which includes rent , pet fee, cleaning fee and fee for renters’ insurance

What is annual housing cost?

The annual housing cost for bainters comprises the annual rent, cleaning fee, pet fee as well as the renters’ insurance, hence, the sum of all the listed cost components form the annual spend on housing for any given year

Year 1:

rent=$1190*12=$14,280

cleaning fee=$75

pet fee=$450

renters’ insurance=$17*12=$204

Year 1 housing cost=$14,280+$75+$450+$204

Year 1 housing cost=$15,009.00

Year 5 housing cost=$14,280*(1+1.7%)^4+$75+$450+$204

Year 5 housing cost=$16,005.08

Year 10 housing cost=$14,280*(1+1.7%)^9+$75+$450+$204

Year 10 housing cost=$17,348.46

Year 15 housing cost=$14,280*(1+1.7%)^14+$75+$450+$204

Year 15 housing cost=$ 18,809.96

Find out more about housing cost on:https://brainly.com/question/28693274

#SPJ1

The the minimum and maximum possible measures of 31 centimeters is {30.5. 31.5}

To find it, one need to add the biggest possible inaccuracy to each measurement, then multiply to get the biggest volume you can. Also Subtract the largest potential mistake from each measurement, then multiply, to to know the smallest volume that can be produced.

Note that the smallest value in the data set is the minimum. The highest value in the data collection is called the maximum.

Since only one data set is given, the  possible measures can only be around it hence the largest and the smallest value close to it.

Learn more about possible measures from

https://brainly.com/question/23655332
#SPJ1

Answer:

No solution

Step-by-step explanation:

5(x + 4) – x = 4(x + 5) – 1

x = ?

Solution:

5(x+4)−x=4(x+5)−1

Apply Distributive property:

Combine Like Terms:

Subtract 4x from both sides:

Subtract 20 from both sides:

There isn't any solutions.

The value of x = 2nπ,  (n ∈ Z) and

\(x=2(n\pi+(-1)^{n} \pi /6)\),  (n ∈ Z)

What are Trigonometric Identities?

Trigonometric Identities are useful whenever trigonometric functions are involved in an expression or an equation. Trigonometric Identities are true for every value of variables  being on both sides of an equation. Geometrically, these identities involve certain trigonometric functions(  similar as sine, cosine, tangent ) of one or  further angles.

According to question

⇒ sin(x/2) + cos(x) - 1 = 0

⇒ sin(x/2) + cos(x) - 1 = 0

{ cos(2x) = 1 - 2sin²(x) }

cos(x) = 1 - 2sin²(x/2)

⇒ sin(x/2) + cos(x) - 1 = 0

⇒ sin(x/2) + 1 - 2sin²(x/2) - 1 = 0

⇒ - 2sin²(x/2) + sin(x/2) + 1 - 1 = 0

⇒ - 2sin²(x/2) + sin(x/2)  = 0

⇒ sin(x/2)(- 2sin(x/2) + 1)  = 0

⇒ sin(x/2) = 0 , x = 2nπ (n ∈ Z)

and

⇒ sin(x/2) = 1/2 , \(x=2(n\pi+(-1)^{n} \pi /6)\) (n ∈ Z)

To Learn more About Trigonometric Identities, Check out :

https://brainly.com/question/24377281

#SPJ1

The tangent line approximation at x= 29.2 is

L(x) = 2x - 1 or L(29.2) = 57.4

The intuitive idea is that a tangent plane “just touches” a surface at a point. The formal definition mimics the intuitive notion of a tangent line to a curve. Let z = f(x,y) be the equation of a surface S in R3, and let P=(a,b,c) be a point on S.

A function f differentiable at tangent.

x=a, we can find that the slope of the tangent of y=f(x) at (a,f(a)) can be found by writing . ). The resulting tangent line through (a,f(a)) and the gradient m=f'(a) is the point-gradient given by

y−f(a)=f'(a)(x−a) has an equation of the form This can also be expressed as y=f'(a)(x−a)+f(a).

Replacing the variable y by the expression L(x) yields points (a, f( a)) called L(x)=f′(a)(x−a)+f(a). , L(x) is just the new name for the tangent, and

f(x)≈L(x) for x near a.

f(x) = 2x - 1

x= 29.0 near to 29.2

f(29.0) = 58 - 1 = 57

f'(x) = 2

So, the point is (29.0, 57) and slope of tangent is 2 .

Tangent line , 57 = 2(29) + b

=> b = -1

then equation is 2x - 1 = y

We to calculate tangent line approximation give as an approximation for at x = 29.2

Tangent line approximation,

y = 2 (29.2) - 1 = 57.4

Learn more about Tangent line at;

https://brainly.com/question/23265136

#SPJ4

The given question is incomplete, complete question is:

Suppose and f (x) = 2x - 1 , what does the tangent line approximation give as an approximation for x= 29.2??