Choose a reasonable estimate.
thickness of a paperback book
A. 25 mm
B. 25 m
C. 25 km
Answers
Answer:
A. 25mm
Step-by-step explanation:
Answer: 25 mm
Step-by-step explanation: No book is ever a meter or kilometer thick.
Related Questions
what is 57.8 divided by 3.4?
Answers
Answer: 17
Step-by-step explanation: 3.4 can go into 57.8 seventeen times. 3.4 x 17 is 57.8. Therefore, 57.8 divided by 3.4 is 17.
Because 3,4 can go into 54.8 seventeen times
an interaction of a binary variable with a continuous variable allows for separate calculation of the slope coefficient on the continuous variable for the two groups defined by the binary variable. T/F
Answers
It is true that an interaction of a binary variable with a continuous variable allows for separate calculation of the slope coefficient on the continuous variable for the two groups defined by the binary variable.
When there is an interaction between a binary variable and a continuous variable in a statistical model, it allows for separate calculation of the slope coefficient on the continuous variable for the two groups defined by the binary variable. This means that the effect of the continuous variable on the outcome can differ between the two groups, and the interaction term captures this differential effect. By including the interaction term in the model, we can estimate and interpret the separate slope coefficients for each group.
To know more about binary variable,
https://brainly.com/question/13950097
#SPJ11
Is 0.5ab a positive number.
Answers
Answer: Yes.
Step-by-step explanation:
Answer: Yes, it is positive
Can u help me with Circles and Composite Figures?
Answers
Answer:
What type 9f composite figure?
Step-by-step explanation:
Pls send an attachment
Answer:
please can you bring the images of the circles and Composite Figures you want us to help you out.
Step-by-step explanation:
There is no attachment so please how can your question be answered.
a special window has the shape of a rectangle surmounted by an equilateral triangle. see the figure. if the perimeter of the window is 16 feet, what dimensions will admit the most light?
Answers
A triangle whose sides are all equal is called an equilateral triangle and its area is given by A=\(\frac{\sqrt{3} }{4}\) \(x^{2}\), where x is the side of the triangle.
The area of a rectangle is found by using the formula
A=lw, where l is the length and w is the width.
The given figure can be split into two shapes: a rectangle and an equilateral triangle as shown in the diagram. Let l be the length of the rectangle.
Add all of the sides of the window and equate their result to 16. Then solve for l.
x + x + l + x + l = 16
3x + 2l = 16
2l = 16 - 3x
l = \(\frac{16-3x}{2}\)
The total area of the window will be the sum of the area of the equilateral triangle ABE and the area of rectangle BCDE.
A = \(\frac{\sqrt{3} }{4}\)\(x^{2}\) + lx
Subsitute \(\frac{16-3x}{2}\) for l into the obtained equation and simplify.
A =\(\frac{\sqrt{3} }{4}\)\(x^{2}\) + ( \(\frac{16-3x}{2}\))x
A = \(\frac{\sqrt{3} }{4} x^{2}\) + 8x - \(\frac{3}{2} x^{2}\)
Differentiate the obtained equation with respect to x and equate the first derivative to 0 to calculate the critical point x .
\(\frac{dA}{dx}\) = \(\frac{\sqrt{3} }{4}\) (2x) + 8 - \(\frac{3}{2}\) (2x)
0 = \(\frac{\sqrt{3} }{2}\) x - 3x + 8
x (3 - \(\frac{\sqrt{3} }{2}\)) = 8
x = \(\frac{16}{6-\sqrt{3} }\)≈3.74887
Again, differentiate the equation
\(\frac{dA}{dx}\) = \(\frac{\sqrt{3} }{2}\)x - 3x + 8 with respect to x.
\(\frac{d^{2}A }{dx^{2} }\) = \(\frac{\sqrt{3} }{2}\) - 3
The value of the second derivative is \(\frac{\sqrt{3} }{2}\)−3, which is negative. This implies that the area will be maximum at the critical point.
Subsitute x = 3.74887 into the equation
l = \(\frac{16-3x}{2}\) and simplify
l = \(\frac{16-(3)(.74887)}{2}\) ≈ 2.3767
The maximum light will enter through the window when the triangular portion will have the side length of 3.74887 feet and the dimensions of the rectangular portion will be 3.74887-ft-by-2.3767-ft.
Learn more about surmounted related word problems by:
https://brainly.com/question/27547781
#SPJ4

Given z= - sqrt 2- sqrt 2i, which letter represents z3
Answers
Answer:
A
Step-by-step explanation:
took test
Answer:
A edge 2021
Step-by-step explanation:
You will receive $500 per year forever starting from 5 -year from today, what is the value of this perpetuity today with 8% of annual interest rate? 3997.34 4125.25 4593.94 5000
Answers
The value of the perpetuity today, with an annual interest rate of 8%, is $4,125.25.
To calculate the present value of a perpetuity, we can use the formula: Present Value = Cash Flow / Interest Rate.
In this case, the cash flow is $500 per year, and the interest rate is 8% (or 0.08 in decimal form). Plugging these values into the formula, we get: Present Value = $500 / 0.08 = $6,250.
However, this calculation gives us the present value of the perpetuity starting from today. Since the payments start 5 years from today, we need to discount the value by the present value of $1 received 5 years from today.
Using the formula for the present value of a single amount, we find that the present value of $1 received 5 years from today, with an 8% interest rate, is approximately 0.6806.
To calculate the present value of the perpetuity starting 5 years from today, we multiply the present value of $6,250 by the discount factor of 0.6806: Present Value = $6,250 * 0.6806 ≈ $4,250.25.
Therefore, the value of the perpetuity today, with an 8% annual interest rate and payments starting 5 years from today, is approximately $4,125.25.
for such more questions on interest
https://brainly.com/question/25720319
#SPJ8
Dante is solving the system of equations below.
r+S-=-4
2r-35+=1
3r-2s+21= 3
He writes the row echelon form of the matrix. Which matrix did Dante write?

Answers
Answer:
The answer is the first matrix. Image attached.
Step-by-step explanation: Given that Dante is solving the system of equations:
In solving the above system of equations, Dante writes the row echelon form of the matrix. We are to select the correct row echelon of the matrix that he wrote.
We know that a matrix is said to be in row echelon form if the leading entry in each nonzero row is a 1 and each column containing a leading 1 has zeros everywhere else.
In the given options, these conditions are satisfied by the first option only. And also, if we write the solution from this matrix, we will have
r = -1, s = 0 and t = 3.
If we substitute these values in the given system, it will get satisfied.
Thus, the first matrix, attached herewith, is the correct matrix.
Your mom is building a garden around a fountain she has a space marked out but decides she wants to enlarge it without altering the center of it what type of transformation is this
Answers
Answer:
u didnt give out the choses but it might be a chance to be dilation
Step-by-step explanation:
"the action or condition of becoming or being made wider, larger, or more open."
since she enlarge it without altering the center of it
Can anyone please help me do 13 and 14 please

Answers
Answer:
hey we can only see 13 and for 13 is X = 57.36
Step-by-step explanation:
since we have opposite and the hypotenuse we use sin...
sin(theta) = opp/hyp
sin(38) = 17/x
and we multiple x to both sides which leaves us with
x * sin(38) = 17
and then divide sin(38) so x can be by it- self which gives us
x = 17/sin(38
X = 57.36
Amy's fish tank has 16 liters of water in it. She plans to add 6 liters per minute until the tank has more than 88 liters. What are the possible numbers of minutes Amy could add water?
Answers
Answer:
12 minutes till 88 liters
Step-by-step explanation:
Verify the parallelogram law for vectors u and v in R^n:?u+v?^2 +?u-v?^2 = 2?u?^2 +2?v?^2 (hint: Use the definition of the norm in terms of the inner product, and then use propertiesof inner product)
Answers
To verify the parallelogram law for vectors u and v in R^n, we will follow these steps:
1. Write the given equation: ||u+v||^2 + ||u-v||^2 = 2||u||^2 + 2||v||^2
2. Use the definition of the norm in terms of the inner product: ||u+v||^2 = and ||u-v||^2 =
3. Use properties of inner product.
Now, let's apply these steps:
Step 1: We have the equation ||u+v||^2 + ||u-v||^2 = 2||u||^2 + 2||v||^2.
Step 2: Replace the norms with their corresponding inner products:
+ = 2 + 2
Step 3: Apply properties of inner products and expand the terms:
(u⋅u + 2u⋅v + v⋅v) + (u⋅u - 2u⋅v + v⋅v) = 2(u⋅u) + 2(v⋅v)
Now, observe that the terms "2u⋅v" and "-2u⋅v" cancel each other out: 2(u⋅u) + 2(v⋅v) = 2(u⋅u) + 2(v⋅v)
As the equation holds true, we have successfully verified the parallelogram law for vectors u and v in R^n using the definition of the norm in terms of the inner product and properties of inner product.
Learn more about parallelogram law here, https://brainly.com/question/15590110
#SPJ11
3m-6n + 2m +4n
PLZZZZ HELPP
Answers
Answer:
5
−
2
Step-by-step explanation:
3
−
6
+
2
+
4
5
−
6
+
4
What is the least common multiple (LCM) of 5 and 12?
Answers
Answer:
60
Step-by-step explanation:
Hope this helps
Answer:
60
Step-by-step explanation:
Someone help me on 103 pls
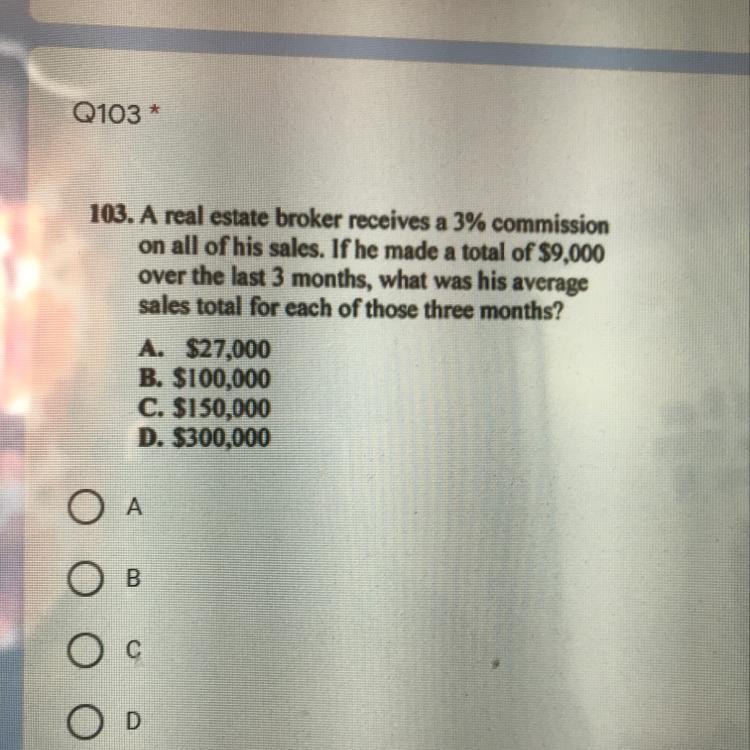
Answers
Answer:
it is A
27000
hope it helps u
Answer:
B
Step-by-step explanation:
3% x = 9000 change the per cent to a fraction
3/100 x = 9000 Multiply by 100
3x = 9000* 100
3x = 9000 00 Divide by 3
x = 900000/3
x = 300000 That is the total for all three months.
You must divide that total by three to get a monthly amount 300000/3
100000
B
Find the center, transverse axis, vertices, foci, and asymptotes. Graph the following equation. y²-16x²-8y-160x-400 = 0
Answers
Given equation of the graph:y² - 16x² - 8y - 160x - 400 = 0We need to find the center, transverse axis, vertices, foci, and asymptotes and graph the given equation of hyperbola.
First, let us write the given equation of the graph in standard form by completing the square.
y² - 16x² - 8y - 160x - 400 = 0
⇒ y² - 8y - 16x² - 160x - 400 = 0
⇒ (y - 4)² - 16x² - 160x - 436 = 0
⇒ (y - 4)² - 16(x² + 10x + 25/4) - 436 + 400 = 0
⇒ (y - 4)² - 16(x + 5)² + 36 = 0
⇒ (y - 4)²/36 - (x + 5)²/9 = 1.
Thus, the given equation is a hyperbola with the center (-5, 4), transverse axis length 2√10, conjugate axis length 2√6, vertices (-5 + √10, 4), (-5 - √10, 4), foci (-5 + √46, 4), (-5 - √46, 4), and asymptotes
y = (2/√3)(x + 5) + 4 and
y = -(2/√3)(x + 5) + 4.
To know more about asymptotes visit:-
https://brainly.com/question/32038756
#SPJ11
In the past month, Ashley rented 3 video games and 1 DVD. The rental price for each video game was $2.70. The rental price for the
DVD was $3.30. What is the total amount that Ashley spent on video game and DVD rentals in the past month?
Answers
Answer:
$11. 40
Step-by-step explanation:
(3×2.70)+3.30=8.10+3.30=$11.40
Answer:
11.40 dollars
Step-by-step explanation:
(2.70*3)+(3.30*1)=
8.10+3.30=
$11.40
Geometry please help! I’ll mark Brainlest

Answers
Answer:
it is 23.
Step-by-step explanation:
The hypotenuse has to be each leg added together which is 44. And 44 - 21 is 23.
Pls mark brainliest.
Use the Integral Test to determine whether the series is convergent or divergent.
[infinity] n
n2 + 6
n = 1
Evaluate the following integral.
[infinity] 1
x
x2 + 6
dx
Answers
The series ∑ₙ=₁ to ∞ (n/n² + 6) is divergent.
To determine whether the series ∑ₙ=₁ to ∞ (n/n² + 6) is convergent or divergent, we can use the Integral Test.
The Integral Test states that if f(x) is a continuous, positive, and decreasing function on the interval [1, ∞) and f(n) = aₙ for all positive integers n, then the series ∑ₙ=₁ to ∞ aₙ and the integral ∫₁ to ∞ f(x) dx either both converge or both diverge.
In this case, let's consider the function f(x) = x/(x² + 6). We can check if it meets the conditions of the Integral Test.
Positivity: The function f(x) = x/(x² + 6) is positive for all x ≥ 1.
Continuity: The function f(x) = x/(x² + 6) is a rational function and is continuous for all x ≥ 1.
Decreasing: To check if the function is decreasing, we can take the derivative and analyze its sign:
f'(x) = (x² + 6 - x(2x))/(x² + 6)² = (6 - x²)/(x² + 6)²
The derivative is negative for all x ≥ 1, which means that f(x) is a decreasing function on the interval [1, ∞).
Since the function f(x) = x/(x² + 6) satisfies the conditions of the Integral Test, we can evaluate the integral to determine if it converges or diverges:
∫₁ to ∞ x/(x² + 6) dx
To evaluate this integral, we can perform a substitution:
Let u = x² + 6, then du = 2x dx
Substituting these values, we have:
(1/2) ∫₁ to ∞ du/u
Taking the integral:
(1/2) ln|u| evaluated from 1 to ∞
= (1/2) ln|∞| - (1/2) ln|1|
= (1/2) (∞) - (1/2) (0)
= ∞
The integral ∫₁ to ∞ x/(x² + 6) dx diverges since it evaluates to ∞.
According to the Integral Test, since the integral diverges, the series ∑ₙ=₁ to ∞ (n/n² + 6) also diverges.
Therefore, the series ∑ₙ=₁ to ∞ (n/n² + 6) is divergent.
To know more about divergent check the below link:
https://brainly.com/question/927980
#SPJ4
Incomplete question:
Use the Integral Test to determine whether the series is convergent or divergent.
∑ₙ=₁ to ∞ = n/n² + 6
Evaluate the following integral ∫₁ to ∞ x/x²+6 . dx
What is the factored form of this expression?
18x2 − 50
Answers
Answer:
_14
Step-by-step explanation:
step1 18×2 -50
step2 18×2 =36_50
step3 36_50=_14
Answer:
2(9*x-25)=18×2-50
Step-by-step explanation:
the answer is in the problem since we know 1 times anything will stay the same. so just divide the other integers by 2 and put the problem in parentheses.
If the probability of a new employee in a fast-food chain still being with the company at the end of the year is 0. 5, what is the probability that out of 8 newly hired people?
Answers
Using binomial distribution, the probability of
a. 5 will still be with the company after 1 year is 28%.
b. at most 6 will still be with the company after 1 year is 89%.
The probability of a new employee in a fast-food chain still being with the company at the end of the year is given to be 0.6, which can be taken as the success of the experiment, p.
We are finding probability for people, thus, our sample size, n = 8.
Thus, we can show the given experiment a binomial distribution, with n = 8, and p = 0.6.
(i) We are asked for the probability that 5 will still be with the company.
Thus, we take x = 5.
P(X = 5) = (8C5)(0.6⁵)((1 - 0.6)⁸⁻⁵),
or, P(X = 5) = (56)(0.07776)(0.064),
or, P(X = 5) = 0.27869184 ≈ 0.28 or 28%.
(ii) We are asked for the probability that at most 6 will still be with the company.
Thus, our x = 6, and we need to take all values below it also.
P(X ≤ 6)
= 1 - P(X > 6)
= 1 - P(X = 7) - P(X = 8)
= 1 - (8C7)(0.6)⁷((1 - 0.6)⁸⁻⁷) - (8C8)(0.6)⁸((1 - 0.6)⁸⁻⁸)
= 1 - 8*0.0279936*0.4 - 1*0.01679616*1
= 1 - 0.08957952 - 0.01679616
= 0.89362432 ≈ 0.89 or 89%.
Learn more about the binomial distribution at
https://brainly.com/question/24756209
#SPJ4
The provided question is incomplete. The complete question is:
If the probability of new employee in a fast-food chain still being with the company at the end of 1 year is 0.6, what is the probability that out of 8 newly hired people,
a. 5 will still be with the company after 1 year?
b. at most 6 will still be with the company after 1 year?
(1 point) evaluate the surface integral ∬s(−2yj zk)⋅ds. where s consists of the paraboloid y=x2 z2,0≤y≤1 and the disk x2 z2≤1,y=1, and has outward orientation.
Answers
The surface integral ∬s(−2yj zk)⋅ds is 0
To evaluate the surface integral ∬s(−2yj zk)⋅ds over the given surface s, we need to first parameterize the surface and then calculate the dot product of the vector field with the surface normal vector, and integrate over the surface.
The given surface s consists of a paraboloid and a disk, and can be parameterized as:
r(x,y) = xi + yj + (x^2y^2)k 0≤y≤1 and x^2 + z^2 ≤ 1, y=1
To find the surface normal vector at each point on the surface, we can take the cross product of the partial derivatives of the parameterization with respect to x and y:
r_x = i + 0j + 2xyk
r_y = 0i + j + x^2*2yk
n = r_x x r_y = (-2xy)i + (x^2*2y)j + k
Since the surface has an outward orientation, we need to use the negative of the normal vector. Thus, we have:
-n = (2xy)i - (x^2*2y)j - k
Now, we can calculate the dot product of the vector field F = (-2yj zk) with the surface normal vector:
F · (-n) = (-2yj zk) · (2xy)i - (-2yj zk) · (x^2*2y)j - (-2yj zk) · k
= -4x^2y^2
Therefore, the surface integral becomes:
∬s(−2yj zk)⋅ds = ∫∫s -4x^2y^2 dS
To evaluate this integral, we can use the parameterization of the surface and convert the surface integral into a double integral over the region R in the xy-plane:
∬s(−2yj zk)⋅ds = ∫∫R -4x^2y^2 ||r_x x r_y|| dA
= ∫[0,1]∫[0,2π] -4r^2 cos^2 θ sin^3 θ dr dθ
= 0 (by symmetry)
Therefore, the value of the surface integral is 0.
Learn more about surface integral at https://brainly.com/question/2303591
#SPJ11
I need help pleasejfjdjs

Answers
Answer:
a) five more than ten b) five groups of ten c) five less than ten d) five into ten
Step-by-step explanation:
Step-by-step explanation:
five less than ten ( c)
five into ten (d)
five groups of ten (b)
five more than ten (a)
14 cm perimeter of circle
Answers
Step-by-step explanation:
Radius = 14 cm
π = 22/7 (Because the value of the circle's radius is the multiples of 7).
• Perimeter :
= 2 . π . r
= 2 . 22/7 . 14
= 28 . 22/7 (Divide 28 and 7 with 7)
= 4 . 22/1
= 4 . 22
= 88 cm is the answer
Khan Academy please show work

Answers
Answer:
Rewriting the equation in the form (x+c)²=d by completing the square
\(\left(x+5\right)^2=16\)The solutions to the quadratic equation are:
\(x=-1,\:x=-9\)Step-by-step explanation:
Given the equation
\(x^2+10x+22=13\)
subtract 22 from both sides
\(x^2+10x+22-22=13-22\)
simplify
\(x^2+10x=-9\)
Rewriting the equation in the form (x+c)²=d by completing the square
\(x^2+10x+5^2=-9+5^2\)
\(x^2+10x+5^2=16\)
\(\left(x+5\right)^2=16\)
\(\mathrm{For\:}f^2\left(x\right)=a\mathrm{\:the\:solutions\:are\:}f\left(x\right)=\sqrt{a},\:-\sqrt{a}\)
solve
\(x+5=\sqrt{16}\)
\(x+5=\sqrt{4^2}\)
\(x+5=4\)
\(x=-1\)
also solving
\(x+5=-\sqrt{16}\)
\(x+5=-4\)
\(x=-9\)
Therefore, the solutions to the quadratic equation are:
\(x=-1,\:x=-9\)
Make your angle measures correct to the nearest degree and side measures to 1 decimal place

Answers
The measure of angle Z is 34°, side length of YZ is 34.1, and the side length of XZ is 41.1. The correct option is the third option ∠Z = 34°, YZ = 34.1, XZ = 41.1
Calculating measures of angles and side measures of a triangleFrom the question, we are to determine the angles measures of and the side measures of the given triangle XYZ
From the given information,
∠Y = 90°
XY = 23
∠X = 56°
First, we will determine the measure of angle Z
m ∠X + m ∠Y + m ∠Z = 180° (Sum of angles in triangle)
56° + 90° + m ∠Z = 180°
m ∠Z = 180° - 56° - 90°
m ∠Z = 34°
Now, since the measure of one of the angles is 90°, ΔXYZ is a right triangle.
Thus,
From SOH CAH TOA, we can write that
tan X = |YZ| / |XY|
∴ tan 56° = |YZ| / 23
|YZ| = 23 × tan 56°
|YZ| = 34.0989
|YZ| ≈ 34.1
Also,
cos X = |XY| / |XZ|
cos 56° = 23 / |XZ|
|XZ| = 23 ÷ cos 56°
|XZ| = 41.1307
|XZ| ≈ 41.1
Hence, ∠Z = 34°, |YZ| = 34.1, and |XZ| = 41.1
Learn more on Calculating measures of angles and side measures of a triangle here: https://brainly.com/question/20734777
#SPJ1
what does 2x+5=8y-17
Answers
Translate a point (x,y) 3 units left and 5 units up. Then translate the image 5 units right and 2 units up. What are the coordinates of the point after the translations?
Answers
Answer:
\((x+2, y+7)\)
Step-by-step explanation:
\((x,y) \longrightarrow (x-3, y+5) \longrightarrow (x+2, y+7)\)
The double number line shows the number of children 1 adult supervises on a field trip. Adults Children Complete the table to show the same information as the double number line: Adults Children 66 15 Nee'
Pls I really need help I'm not the well at math

Answers
The number of 8 adults will supervise 48 children, 66 children will be supervised by 11 adults and 15 adults will supervise 90 children.
According to the question,
We have the following information:
1 adult supervises 6 children.
Now, for the first one, we have to find number of children to be supervised by 8 adults.
1 adult = 6 children
8 adults = 8*6 children
8 adults = 48 children
Now, for the second one, we have to find the number of adults for 66 children:
1 children = 1/6 adult
66 children = 66/6 adults
66 children = 11 adults
Now, for the third one, we have to find number of children for 15 adults:
15 adults = 15*6 children
15 adults = 90 children
Hence, the number of 8 adults will supervise 48 children, 66 children will be supervised by 11 adults and 15 adults will supervise 90 children.
To know more about number here
https://brainly.com/question/1340474
#SPJ1
Answer: First is 48 Second is 11 Third is 90
Step-by-step explanation: I did it on Khan ✔
i really need somebody to help me with this question. i’m gonna fail. this is year 8 maths btw.

Answers
Answer:
Three questions for the equation 18 × y^3 :-
9y × 2y^26y^2 × 3y18 × 1y^3hope it helps!