Solve each system by substitution.

x² - y = x + 4 x-1 = y + 3

Answer: (v + 7)(v -3)

Step-by-step explanation:

(v +7)(v -3)

v x v = v^2

v x -3 = -3v

7 x v = 7v

7 x -3 = -21

v^2 -3v +7v -21 = v^2 +4v -21 = 0

Answer:

The answer is (v - 3)(v + 7).

Step-by-step explanation:

First, you have to elaborate it :

v² + 4v - 21 = 0

v² - 3v + 7v - 21 = 0

Next, you have to collect like terms :

v(v - 3) + 7(v - 3) = 0

(v - 3)(v + 7) = 0

In order to determine whether the vector -GH is tangent to the vector ®F, we need to analyze their directions and compare them.

If two vectors are tangent to each other, it means they share the same direction. In other words, they are parallel.

Let's break down the problem:

GH is a vector. Since it is denoted as -GH, we can assume that GH is a vector in the opposite direction of -GH.

®F is also a vector, but we don't have any specific information about its direction or magnitude.

Without knowing any additional details about the vectors GH and ®F, we cannot determine whether -GH is tangent to ®F. The information provided is insufficient for making a conclusive judgment.

To determine tangency or parallelism between two vectors, we would need information about their directions, magnitudes, or any other relationships that could be established between them.

Learn more about vector from the given link:

https://brainly.com/question/28028700

#SPJ11

Answer:

1/18

Step-by-step explanation:

1 yd = 36 in., so 3 yd = 108 in.

The scale is 6 in. to 108 in., or 6/108.

Divide the numerator and denominator by 6.

6/108 = 1/18

Answer: 1/18

Given parameters:

Elevation of Town M = 282ft

Elevation of Town R = 679ft

Unknown:

How much higher is Town R than M = ?

Solution:

Town M lies below the sea level whereas Town R is above the sea level.

     Graphically:

                                    Town R   679ft

                                         ↑

                                         ↑

                                         ↑

                                         ↑

                                    ↔↔↔  Sea level

                                         ↓

                                         ↓

                                    Town M     282ft

Town R is 282ft + 679ft higher than Town M  = 961ft

Answer:

8 cm is the answer

Step-by-step explanation:

Answer:

See Explanation

Step-by-step explanation:

\(

\because \sin\bigg(\frac{\pi}{2} + x\bigg)= \cos x\\

\&\: \sin (\pi - x) = \sin x\\\\

Now,

\frac{\sin\bigg(\frac{\pi}{2} + x\bigg)}{\sin (\pi - x)} = \cot x\\\\

LHS

= \frac{\sin\bigg(\frac{\pi}{2} + x\bigg)}{\sin (\pi - x)} \\\\

=\frac{\cos x}{sinx} \\\\

= \cot x\\\\

= RHS\\\\

Hence\: Proved

\)

Answer

The equation has infinitely many solutions.

Since 12 is always equal to 12, the equation will have infinitely many solutions.

Explanation

4 (4x + 3) = 19x + 9 - 3x + 3

4(4x) + 4(3) = 19x + 9 - 3x + 3

16x + 12 = (19x - 3x) + (9 + 3)

16x + 12 = 16x + 12

Subtract 16x from both sides

16x - 16x + 12 = 16x - 16x + 12

12 = 12

Since 12 is always equal to 12, the equation will have infinitely many solutions.

Hope this Helps!!!

when 347 is divided by 7 it's gives:

Quotient:

Reminder:

Answer:

quotient is 49

and remainder is

Step-by-step explanation:first step is divide 347 by the divisor 7 you will get the quotient 49 and 4will remain as remainder because t can not be divided by divisor.

Answer:1:2

Step-by-step explanation:

it is this answer because you have 2 circles for 4 triangles, you can simplify that by dividing each number by 2 and you get 1 and 2

Answer:

1:2

Step-by-step explanation:

it would originally be 2:4 But both are divisible by 2 so they simplify down to 1:2........2÷2=1 and 4÷2=2 since the ratio has to be circles to triangle the 1 goes first then the 2

The people are moving apart at a rate of 500.02 feet per 15 minutes, which is approximately 33.34 feet per minute. Hence, the rate at which the people are moving apart 15 minutes after the woman starts walking is 33.34 feet per minute.

A man and a woman start walking in opposite directions from two different points. The man starts 4 feet north of a point P, while the woman starts 500 feet due east of P. The man started walking 5 minutes before the woman. To solve the problem, the Pythagorean theorem is used.

By applying the Pythagorean theorem, a diagram is drawn, and the following distances are assumed: The man is 4 feet away from point P, and the woman is 5 feet away from the point 500 feet east of P. The total time elapsed is 15 minutes, with the man walking for 20 minutes (since he started 5 minutes earlier than the woman).

Using the formula distance = speed x time, the distances traveled by the man and the woman are calculated. The man's speed is 4 feet per minute, and the woman's speed is 5 feet per minute. The man travels a distance of 80 feet, and the woman travels a distance of 75 feet.

Applying the Pythagorean theorem again, the distance between the man and the woman is found. It is calculated as the square root of [(500 feet)^2 + (80 feet - 75 feet)^2], resulting in a distance of 500.02 feet.

To know more about Pythagorean theorem Visit:

https://brainly.com/question/14930619

#SPJ11

Step-by-step explanation:

For g(x) = f(x) + 5:

Because f(x) = x, this can be simplified to:

y = x + 5

For h(x) = 2 * f(x) - 3, simplified to:

2*x - 3 or 2x - 3

For j(x) = \(\frac{1}{2} * f(x) - 1\), simplified it is

\(\frac{1}{2}x - 1\)

For f(x), this can be drawn relatively easy, it is a linear line starting at the coordinates (0,5) gradually increasing by 1 in both the y and x axis. It can be drawn parallel to the line given in your question just one above.

For h(x), the line will start at (0, -3) but then have an incline of 2, i.e. the second point would be at 1, -1, and the third at (3, 3). This is because you are doubling the value of x but subtracting 3.

For j(x), x is halved so the line will be less steep although it will start at the coordinate (0, -1) because 1 is being subtracted.

Hope this helps!

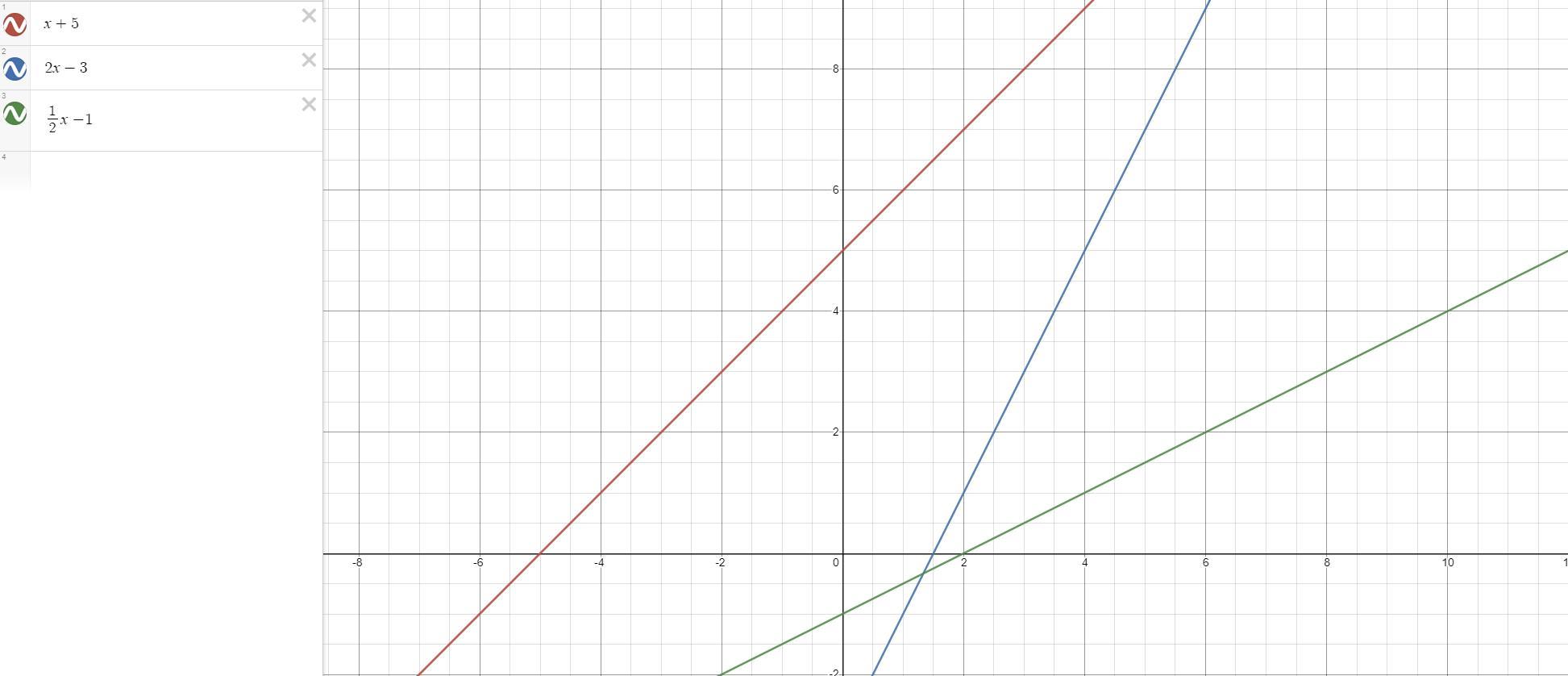
Answer:

This is only for the first part. Please see the attached image for the graphs of the three given functions.

Step-by-step explanation:

1. g(x) = f(x) + 5

This involves the vertical shift of 5 units.  

Start by solving for the y-intercept. The y-intercept is the value of y (or g(x) when x (or f(x) )  = 0:

Substitute f(x) with 0:

g(x) = f(x) + 5

g(x) = 0 + 5

g(x) = 5

The y-intercept is (0, 5)

According to one of the hints provided in your instruction, it states that you can use the slope to find another point.  

In your given function, g(x) = f(x) + 5, the slope is 1 (it is implied, meaning, if your function is rewritten in its slope-intercept form, it is y = x + 5, in which your slope is implied as 1/1 or 1). So, to find another point, from the y-intercept (0, 5), you can go 1 unit up, and 1 unit to the right, which gives you the next point: (1, 6). Likewise, to go to the opposite direction, you can go down 1 unit, and 1 unit to the left.  

2.  h(x) = 2 * f(x) - 3

The slope of this function is 2, and the y-intercept is -3.  If you rewrite h(x) = 2 * f(x) - 3 into its slope-intercept form, it will be: y = 2x - 3. That is why the slope (m) = 2, and the y-intercept (b) = -3.  

To start, we can find the y-intercept, which is, again, the value of y (or h(x)) when f(x) = 0:

h(x) = 2 * 0 - 3

h(x) = 0 - 3

h(x) = -3

Therefore, the y-intercept is (0, -3). This can be your starting point to draw a line.  

From this point, you can use the slope (2/1) to find more points by going up 2 units, and 1 unit to the right. You'll end up with the next point, (1, -1).  Likewise, to go on the opposite direction, you can go 2 units down, and 1 unit to the left.  

3. j(x) = ½* f(x) - 1

The slope of this function is 1/2, and the y-intercept is -1. If you rewrite j(x) = ½* f(x) - 1 into its slope-intercept form, it will be: y = 1/2x - 1. That is why the slope (m) = ½, and the y-intercept (b) = -1.  

Same as the previous steps, you can start with the y-intercept by setting f(x) = 0:

j(x) = ½* f(x) - 1

j(x) = ½* 0 - 1

j(x) = 0 - 1

j(x) = - 1

Therefore, the y-intercept is (0, -1). Same as the previous functions, you can use the slope (m = ½) and start going 1 unit up, and 2 units to the right to get to the next point, (2, 0).  Keep going until you have enough points to connect and draw a line with.

Please see the attached image for the graph.  

Answer:

x= 4

Step-by-step explanation:

Please see the attached pictures for the full solution.

Answer:

it would be 39t for the extra 8s

Step-by-step explanation:

To find the parametric equations for the path of a particle moving along a circle with 0 ≤ t ≤ π, we'll start by considering the equation of a circle with radius r centered at (h, k):
(x-h)² + (y-k)² = r²
Now, to create parametric equations, we'll express x and y in terms of a parameter, t. In this case, t represents the angle (in radians) that the particle has traveled along the circle.
We can use the trigonometric functions sine and cosine to do this. For a circle with radius r centered at (h, k), the parametric equations will be:
\(x(t) = h + r*cos(t)\)
\(y(t) = k + r*sin(t)\)
Since we're given a range for t (0 ≤ t ≤ π), this means that the particle moves along a semicircle, starting at the initial point (h+r, k) when t=0 and ending at the point (h-r, k) when t=π.
To summarize, the parametric equations for a particle moving along a circle with radius r and center (h, k) for 0 ≤ t ≤ π are:
\(x(t) = h + r*cos(t)\)
\(y(t) = k + r*sin(t)\)

for such more questions on trigonometric functions

https://brainly.com/question/1143565

#SPJ11

Answer:-60

Step-by-step explanation:

Lets start by adding 3 to both sides.

\(\frac{1}{4}y-3=-18\) -->\(\frac{1}{4}y-3+3=-18+3\)-->\(\frac{1}{4}y=-15\)

\(\frac{1}{4}y=-15\)

Now that we have this, we can multiply both sides by 4, the reciprocal of 1/4.

\(\frac{1}{4}y\cdot4=-15\cdot4\)

\(y=-60\)

Answer:

Step-by-step explanation:

1/4y - 3 = - 18

1/4y = -18 + 3

1/4y = 15

y = 15 : 1/4

y = 15 × (-4)

y = -60

---------------------------

check

1/4 × (-60) - 3 = -18

-15 - 3 = -18

-18 = -18

the answer is good

Answer:

The answer would be 2000

Step-by-step explanation:

Answer:

1) 48

2)44

Step-by-step explanation:

Answer:  48 44 Are The Correct Answers

Step-by-step explanation:Hope This Helps

Answer: 8.94

Step-by-step explanation:

each side is the \(\sqrt{20}\) so multiply that by 2 and you will have 8.94

Answer:

\( {x}^{3} + 2 {x}^{2} - 15x \\ x( {x}^{2} + 2x - 15) \\ x( {x}^{2} + 5x - 3x - 15) \\ x(x(x + 5) - 3(x + 5) \\ x((x + 5)(x - 3)) \\ {x}^{2} -7x + - 12 \\ {x}^{2} - 4x + 3x - 12 \\ x(x - 4) + 3(x - 4) \\ (x - 4)(x + 3) \\ 3 {x}^{2} - 27 \\ 3( {x}^{2} - 9) \\ 3((x + 3)(x - 3)) \\ \\ the \: hcf \: = (x + 3)\)

Answer:

896

Step-by-step explanation:

The least common multiple (LCM) of 16, 28, and 56 is 896. This can be determined by listing the multiples of 16, 28, and 56 and then finding the smallest number that is a multiple of all three numbers. The multiples of 16 are 16, 32, 48, 64, 80, 96, 112, 128, 144, 160, 176, 192, 208, 224, 240, 256, 272, 288, 304, 320, 336, 352, 368, 384, 400, 416, 432, 448, 464, 480, 496, 512, 528, 544, 560, 576, 592, 608, 624, 640, 656, 672, 688, 704, 720, 736, 752, 768, 784, 800, 816, 832, 848, 864, 880, 896, etc. The multiples of 28 are 28, 56, 84, 112, 140, 168, 196, 224, 252, 280, 308, 336, 364, 392, 420, 448, 476, 504, 532, 560, 588, 616, 644, 672, 700, 728, 756, 784, 812, 840, 868, 896, etc. The multiples of 56 are 56, 112, 168, 224, 280, 336, 392, 448, 504, 560, 616, 672, 728, 784, 840, 896, etc. The smallest number that is divisible by 16, 28, and 56 is 896, so 896 is the least common multiple of 16, 28, and 56.

Answer:

5q + 2d = 270

Step-by-step explanation:

right on edge .

Answer:

C:5q + 2d = 270 is your answer

Step-by-step explanation:

Answer:

B

Step-by-step explanation:

m

The volume of the solid is 29.865 cubic units.

We have,

To find the volume of the solid generated by revolving region R around the line y = 6, we can use the method of cylindrical shells.

The volume of the solid can be obtained by integrating the area of each cylindrical shell.

Each shell is formed by taking a thin vertical strip of width dx from region R and rotating it around the line y = 6.

Let's denote the radius of each cylindrical shell as r(x), where r(x) is the distance from the line y = 6 to the curve y = 2tan(\(x^5\)).

Since the shell is formed by revolving the strip around y = 6, the radius of the shell is given by r(x) = 6 - 2tan(\(x^5\)).

The height of each cylindrical shell is the difference in x-values between the curve y = 5 - x and the y-axis, which is given by h(x) = x.

The differential volume of each cylindrical shell is given by:

dV = 2π x r(x) x h(x) x dx.

To find the total volume of the solid, we integrate the differential volume over the interval where region R exists, which is determined by the intersection of the curves y = 2tan(\(x^5\)) and y = 5 - x.

The volume V is given by the integral:

V = ∫[a,b] 2π x (6 - 2tan(\(x^5\))) x dx

Setting the two equations equal to each other, we have:

2tan(\(x^5\)) = 5 -x

Let's use numerical approximation to find the intersection points.

Using a numerical solver, we find that one intersection point is approximately x ≈ 1.051.

Now, we can set up the integral to find the volume of the solid:

V = ∫[a,b] 2π  (6 - 2tan(\(x^5\))) x dx

Since we are revolving around the line y = 6, the limits of integration will be from x = 0 to x = 1.051.

V = ∫[0,1.051] 2π  (6 - 2tan(\(x^5\))) x dx

The integral does not have an elementary antiderivative, so we cannot find the exact value of the integral.

However, we can still approximate the value using numerical methods or software.

Using numerical approximation methods, the volume is approximately V ≈ 29.865 cubic units.

Thus,

The volume of the solid is 29.865 cubic units.

Learn more about the volume of solids here:

https://brainly.com/question/32732534

#SPJ12

Answer:

The slope or gradient of a line is a number that describes both the direction and the steepness of the line.

Step-by-step explanation:

Slope is calculated by finding the ratio of the "vertical change" to the "horizontal change" between (any) two distinct points on a line.

Answer:

a) He calculated the area, not the circumference. The equation for the area of a circle is πr², while the equation for the circumference is 2πr.

b) He would need at least 3 quarts of paint. 200.96/75≈2.68 He would need that approximately 2.68 quarts of paint, but I suppose the question is asking you the least amount of whole number quarts of paint. The answer for that would then be 3.

The R9,000 loan offer can be analyzed as follows;

A loan is a financial agreement that is made between a lender and a borrower, such that the borrower accepts a certain amount of money provided by the lender, which is to be paid back after a specified period of time, with an interest.

The total amount which has to be paid as repayment for the loan can be obtained by finding the product of the monthly installment and the total number of months to repay the loan:

Total amount Theo pays = R318.92 × 48 = R15308.16

The reasons banks and other financial institutions offer loans to people that did not apply for loans includes;

Theo's investment options can be analyzed as follows;

Option 1: Investment with simple interest calculation

Interest earned = R9,000 × 8% × 4 years = R2,880

The total value of the investment after 4 years = R9,000 + R2,880 = R11,880

Option 2: Investment with compound interest calculation

The total value of the investment after 4 years = R9,000 × (1 + 7%)⁴ = R11,797.16409

Learn more on compound interest here: https://brainly.com/question/17578515

#SPJ1

Answer:

a) y = \(\frac{7}{17}\)

b) x = 4

Step-by-step explanation:

a) \(\frac{3y+2}{5} =4y-1\)

3y + 2 = 20y - 5

2 = 20y - 3y - 5

2 = 17y - 5

2 + 5  = 17y

7 = 17y

y = \(\frac{7}{17}\)

b) x² + 5 = 21

x² = 21 - 5

x² = 16

x = √16

x = 4

Check the attachment... hope it helps :)

x= +4 or -4

y= 7/17