Solve each matrix equation. [2 -6 8] + [-1 -2 4] = X
Answers
The solution to the matrix equation is X = [1 -8 12].
The matrix equation [2 -6 8] + [-1 -2 4] = X can be solved as follows:
First, we perform the addition of the two matrices on the left side:
[2 + (-1) -6 + (-2) 8 + 4] = [1 -8 12].
Therefore, the solution to the matrix equation is X = [1 -8 12].
To solve the matrix equation, we simply add the corresponding elements of the two matrices. In this case, we add the elements in the first row, then the elements in the second row, and finally the elements in the third row. The resulting matrix is the solution to the equation.
In the given equation, we have:
[2 -6 8] + [-1 -2 4] = [2 + (-1) -6 + (-2) 8 + 4] = [1 -8 12].
Hence, the solution to the matrix equation is X = [1 -8 12]. This means that the sum of the matrices [2 -6 8] and [-1 -2 4] is equal to the matrix [1 -8 12].
Learn more about matrix here:
https://brainly.com/question/29132693
#SPJ11
Related Questions
Write the conditional statement that the venn diagram illustrates.
Ex bisects
Pls help ASAP due soon

Answers
Answer:
if it is a square, then it is a quadrilateral
Step-by-step explanation:
Answer for brainliest.

Answers
hope this can help
In S
3
, find the elements α and β such that ∣α∣=2,∣β∣=2, and ∣αβ∣=3.
Answers
To find the elements α and β such that ∣α∣=2, ∣β∣=2, and ∣αβ∣=3 in S₃, we can consider the elements of the symmetric group S₃ which consists of the permutations of three elements. Let's denote the elements of S₃ as (1 2), (1 3), and (2 3), where (a b) represents the permutation that swaps a and b.
To satisfy the given conditions, we need to find two permutations α and β such that the absolute values of their cycles are equal to 2 and the absolute value of the cycle resulting from their product is equal to 3.
One possible solution is α = (1 2) and β = (1 3).
For α = (1 2), the absolute value of its cycle is 2 since it swaps 1 and 2. Similarly, for β = (1 3), the absolute value of its cycle is also 2 as it swaps 1 and 3.
Now, let's calculate the product αβ. (1 2)(1 3) = (1 3 2), which has a cycle length of 3, satisfying ∣αβ∣=3.
Therefore, one possible solution is α = (1 2) and β = (1 3) in S₃.
Learn more about symmetric group
https://brainly.com/question/33068648
#SPJ11
can someone answer this question really quick
Simplify the expression by combining like terms.
43a−12b+13a+52b
Enter your answer as an expression, like this: 42x+53
Answers
Answer:
56a+40b
Step-by-step explanation:
43a plus 13a is 56a, -12b + 52b is 40b, together it's 56a+40b
if y varies directly as the square root of x and y=3, x=3. calculate y when x=64
Answers
Answer:
y = 64√3
Step-by-step explanation:
Step(i):-
Given that the 'y' varies directly as √x
⇒ y∝ √x
⇒ y = k√x
Put y=3 and x=3
3 = k ×√3
√3 k = √3×√3
After cancellation '√3' on both sides, we get
k = √3
Step(ii):-
Given that x=64 and k = √3
We have a function y = k√x ..(i)
substitute x =64 and k = √3 in equation (i)
y = √3 × 64
y = 64√3
the perimeter of a triangle is 187 feet. the longest isde of the triangle is 12 feet shorter than twice the shortest side. the sum of th lengths of th etwo shorter sides is 35 feet more than the length of the longest side. find the lengths of the sides of the triangle
Answers
Answer:
\(\mathrm{43ft,\ 76ft\ and\ 68ft}\)
Step-by-step explanation:
\(\mathrm{Let\ the\ shortest\ side\ of\ the\ triangle\ be\ x.\ Then,\ the\ longest\ side\ of\ the\ triangle}\\\mathrm{will\ be\ 2x-10.}\\\mathrm{Let\ the\ length\ of\ remaining\ side\ of\ the\ triangle\ be \ y.}\\\mathrm{Given,}\\\mathrm{Sum\ of\ two\ shorter\ sides=35+longest\ side}\\\mathrm{or,\ x+y=35+(2x-10)}\\\mathrm{or,\ y=25+x........(1)}\\\mathrm{Also\ we\ have}\\\mathrm{Perimeter\ of\ triangle=187ft}\\\mathrm{or,\ x+(2x-10)+y=187}\\\mathrm{or,\ 3x+y=197}\\\mathrm{or,\ y=197-3x...........(2)}\)
\(\mathrm{Equating\ equations\ 1\ and\ 2,}\\\mathrm{25+x=197-3x}\\\mathrm{or,\ 4x=172}\\\mathrm{or,\ x=43ft}\\\mathrm{i.e.\ length\ of\ shortest\ side=43ft}\\\mathrm{Now,\ length\ of\ longest\ side=2x-10=2(43)-10=76ft}\\\mathrm{Finally,\ length\ of\ third\ side=y=25+x=68ft}\)
\(\mathrm{So,\ the\ required\ lengths\ of\ triangle\ are\ 43ft,\ 76ft\ and\ 68ft.}\)
The numbers in the triangles below go together following the
4
9
8
7
3
2
6
Find the missing number.
A 1
B 3
Answers
Answer:
1
by looking only 1 is missing
mrh ch07 309 you are working at a boat manfacturer, and want to test your new material under different frequency and corrosive liquid conditions. your boss is nearly certain that salt water is highly corrosive and will be associated with more defects. you have two frequencies of motor which could be used, low frequency and high frequency. you probably guessed it, but low frequency is your low factor here, and high frequency is your high factor here. you have two different liquids, distilled water (which is your low factor) and salt water (your high factor here). this simulates lakes and rivers vs. open ocean use. you run the tests in randomized order, all for the same duration, and count the number of defects observed. lower numbers of defects are better. you have a total of 16 runs. how many replications do you have? enter your answer rounded to the nearest integer.
Answers
You have 4 replications for each treatment combination.
In this scenario, you have two factors: frequency (low and high) and liquid (distilled water and salt water). Each factor has two levels, making a total of four treatment combinations (low frequency with distilled water, low frequency with salt water, high frequency with distilled water, high frequency with salt water).
Since you have a total of 16 runs, the number of replications for each treatment combination can be determined by dividing the total number of runs by the number of treatment combinations. In this case, 16 runs divided by 4 treatment combinations gives you 4 replications per treatment combination.
Know more about combination here:
https://brainly.com/question/31596715
#SPJ11
help! i cant figure this out.

Answers
Answer:
65 cm squared
Step-by-step explanation:
if the area of circular pond is 154 π square meter, find the radius of it's base
Answers
Answer:
r= 12.4m (3 s.f.)
Step-by-step explanation:
Area of circle= πr², where r is the radius
154π= πr²
Divide both sides by π:
154= r²
r²= 154
Square root both sides:
\(r = \sqrt{154} \)
r= 12.4m (3 s.f.)
Answer:
The radius of circular pond is 12.4 m.
Step-by-step explanation:
Given :
➠ Area of circular pond = 154πTo Find :
➠ Radius of circular pondUsing Formula :
\(\star\small{\underline{\boxed{\sf{\red{Area_{(Circle)} = \pi{r}^{2}}}}}}\)
»» π = 22/7»» r = radiusSolution :
Finding the radius of circular pond by substituting the values in the formula :
\({\dashrightarrow{\sf{Area_{(Circle)} = \pi{r}^{2}}}}\)
\({\dashrightarrow{\sf{154 \pi = \pi{r}^{2}}}}\)
\({\dashrightarrow{\sf{154 \times \dfrac{22}{7} = \dfrac{22}{7} \times {r}^{2}}}}\)
\({\dashrightarrow{\sf{154 \times \cancel{\dfrac{22}{7}} = \cancel{\dfrac{22}{7}} \times {r}^{2}}}}\)
\({\dashrightarrow{\sf{154 = {r}^{2}}}}\)
\({\dashrightarrow{\sf{r = \sqrt{154} }}}\)
\({\dashrightarrow{\sf{r \approx 12.4 }}}\)
\(\star{\underline{\boxed{\sf{\purple{r \approx 12.4 \: m }}}}}\)
Hence, the radius of circular pond is 12.4 m.
\(\rule{300}{1.5}\)
Consider a linear time-invariant system with input autocorrelation Rx(τ)=sinc2((a+2)τ) and impulse response h(t)=rect(t−(a+1))). Determine the output energy spectral density ψy(f).
Answers
The output energy spectral density ψy(f) is \(sinc^2\)(f) * rect(f/(a+2)).
To determine the output energy spectral density ψy(f), we need to find the Fourier transform of the autocorrelation function Rx(τ) and multiply it by the magnitude squared of the Fourier transform of the impulse response H(f).
Given:
Rx(τ) = \(sinc^2\)((a+2)τ)
h(t) = rect(t-(a+1))
First, let's find the Fourier transform of Rx(τ):
Rx(f) = F{Rx(τ)} = F{\(sinc^2\)((a+2)τ)}
Using the property of the Fourier transform, the squared sinc function transforms to a rectangular function:
Rx(f) = rect(f/(a+2))
Next, let's find the Fourier transform of the impulse response h(t):
H(f) = F{h(t)} = F{rect(t-(a+1))}
Using the shifting property of the Fourier transform, we get:
H(f) = \(e^{-j2\pi f(a+1)\)sinc(f)
Now, we can calculate the output energy spectral density ψy(f) by multiplying the Fourier transforms of Rx(τ) and h(t):
ψy(f) = \(|H(f)|^2\) * Rx(f)
ψy(f) = \(|e^{-j2\pi f(a+1)}sinc(f)|^2\) * rect(f/(a+2))
Simplifying, we have:
ψy(f) = \(sinc^2\)(f) * rect(f/(a+2))
Therefore, the output energy spectral density ψy(f) is \(sinc^2\)(f) multiplied by a rectangular function centered at f/(a+2).
To learn more about spectral density here:
https://brainly.com/question/29220472
#SPJ4
9.
Challenge yourself
10. Calculate the answers to these problems:
10.1 (-4)2 + (-1)³
10.3 -27-(-2)²
10.5 (1)-(³
10.7 √0,04+ (0,5)²
10.9 0,027+ (0,2)3
088
10.2 -62 33
10.4 ()²+(-1)³
10.6 (0,1)2 + (0,1)3
10.8 √0,0144 - (- 0,2)²
Answers
Answer:
Below
Step-by-step explanation:
Answer 10.1: 15
Explanation:
(-4)^2 is 16 and (-1)^3 is -1, so (-4)^2 + (-1)^3 = 16 - 1 = 15.
Answer 10.3: -23
Explanation:
(-2)^2 is 4 and -27 minus 4 is -23.
Answer 10.5: None
Explanation:
The expression is incomplete as there is no number or operation after the "^3".
Answer 10.7: 0.7
Explanation:
√0.04 is 0.2 and (0.5)^2 is 0.25, so 0.2 + 0.25 = 0.45. The square root of 0.45 is approximately 0.671.
Answer 10.9: 0.02788
Explanation:
(0.2)^3 is 0.008 and 0.027 plus 0.008 is 0.035. Raising 0.035 to the power of 1/3 gives approximately 0.315. Therefore, the final answer is approximately 0.02788.
Answer 10.2: -2018
Explanation:
Using the order of operations, we start with 62 divided by 3 which is approximately 20.67, then multiply that by -33 to get approximately -682.44.
Answer 10.4: -2
Explanation:
Empty brackets imply multiplication. Therefore, ()^2 is 0, and (-1)^3 is -1. Thus, 0 - 1 = -1.
Answer 10.6: 0.11
Explanation:
(0.1)^2 is 0.01 and (0.1)^3 is 0.001, so 0.01 + 0.001 = 0.011.
Answer 10.8: 0.38
Explanation:
0.0144 + 0.04 = 0.0544, and the square root of 0.0544 is approximately 0.2336. Subtracting (-0.2)^2 (which is 0.04) from 0.0544 gives 0.0144. Taking the square root of 0.0144 gives approximately 0.12. Finally, 0.2336 minus 0.12 is approximately 0.38.
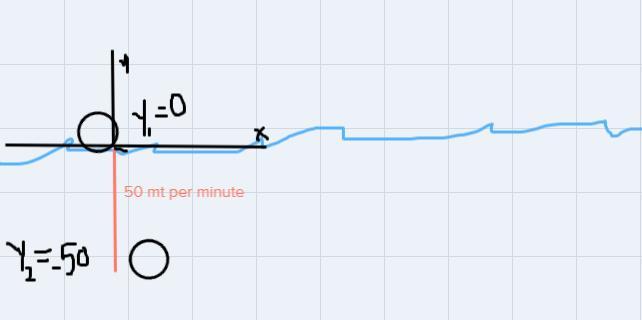
A submarine dove from the surface at a rate of 50 meters per minute. It is now at a depth of 450 meters. Write a numeric equation using negatives to show the number of minutes it took to get to the current depth.
Answers
Explanation
Step1
let
\(\begin{gathered} \text{rate}=-50\frac{mt}{\text{sec}} \\ \text{rate}=\frac{dis\tan ce}{\text{time}} \end{gathered}\)\(\begin{gathered} y_1=initial\text{ position=0} \\ y_2=\text{ final positivion=-50} \\ \text{time}=\text{ 1 minute} \end{gathered}\)Step 2
equation
\(\begin{gathered} time=\text{ }\frac{\text{distance}}{-50}\text{ Equation(1)} \\ \\ \text{replacing} \\ \text{time}=\frac{-450\text{ mt}}{-50\text{ }\frac{mt}{\min}} \\ \text{time}=9\text{ minutes} \end{gathered}\)I hope this helps you
the graph of y=3x^4-16x^3+24x^2+48 is concave down for
Answers
The graph of y=3x^4-16x^3+24x^2+48 is concave down for x values greater than or equal to 0.
The graph of y=3x^4-16x^3+24x^2+48 is an example of a polynomial function. To determine the concavity of a polynomial function, we must first identify the intervals where the function is increasing and decreasing. In this case, the function is increasing for all x values greater than or equal to 0.
Next, we must find the second derivative and determine the intervals where the second derivative is negative. If the second derivative is negative, then the graph is concave down. For this polynomial, the second derivative is y'' = -48x + 48, which is negative for all x values greater than or equal to 0. This means that the graph of y=3x^4-16x^3+24x^2+48 is concave down for all x values greater than or equal to 0.
Learn more about Graphs here:
https://brainly.com/question/24335034
#SPJ4
Find the exact volume of the following.
12 mm
12 mm

Answers
Answer:
V = 144π mm³
Step-by-step explanation:
the volume (V) of a cone is calculated as
V = \(\frac{1}{3}\) πr²h ( r is the radius of the base and h the height of the cone )
here diameter of base = 12 , then r = 12 ÷ 2 = 6 and h = 12 , then
V = \(\frac{1}{3}\) π × 6² × 12
= \(\frac{1}{3}\) π × 36 × 12
= π × 12 × 12
= 144π mm³
The Volume of Cone is 144π mm³.
We have,
Diameter of Base= 12 mm
Radius of Base = 6 mm
Height of Cone = 12 mm
So, the formula for Volume of Cone
= 1/3 πr²h
= 1/3 π (6)² 12
= 4 x 36π
= 144π mm³
Learn more about Volume of Cone here:
https://brainly.com/question/29767724
#SPJ1
determine the minimum or maximum value of the function f(x)= -2x^2+4x+4
Answers
Answer:
-2x^2+4x+4= -4x+ 4x+4= 4
so the answer is 4
done
Jill is baking a pumpkin pie. The recipe calls for 4 ⅓ cups of flour, but Jill has 2 ⅘ cups. How many cups of flour does Jill need?
Answers
Answer:
1 8/15
Step-by-step explanation:
We need to equal the denominators. We have 1/3 and 4/5, and we need to make the bottom numbers equal to each other. The closest common factor is 15 (which we got from 3 x 5). With the denominators solved, we now need to equal out the top numbers, or the numerators. 1 x 5 gives us 5/15, and 4 x 3 gives us 12/15. Then, we need to apply these to each variable. This gives us Jill's 2 12/15th cups of flour, and the recipe's call for 4 5/15 cups. We then subtract these from each other, giving us 1 8/15 cups of flour is needed from Jill.
let f and g be the functions given by f(x) = xe^x^3 write the first four nonzero terms and the genernal term of the taylor series
Answers
The general term of the Taylor series for f(x) = xe^(x^3) centered at x = 0 is (x^(3n+1)) / n!
The first four non-zero terms of the Taylor series for the function f(x) = xe^(x^3) centered at x = 0, along with the general term, are as follows:
f(0) = 0
f'(x) = e^(x^3) + 3x^3 e^(x^3)
f'(0) = 1
f''(x) = (6x^6 + 9x^2 + 1) e^(x^3)
f''(0) = 1
f'''(x) = (54x^9 + 81x^5 + 27x) e^(x^3)
f'''(0) = 0
The general term of the Taylor series for f(x) can be written as:
f^(n)(0) / n! * x^n
where f^(n) denotes the nth derivative of f. Therefore, the general term of the Taylor series for f(x) = xe^(x^3) centered at x = 0 is:
(x^(3n+1)) / n!
Learn more about Taylor series here
https://brainly.com/question/23334489
#SPJ11
Consider the following linear programming problem
maximize z=−x
1
+3x
2
subject to x
1
+3x
2
≤5
−x
1
+x
2
≤1
x
1
+x
2
≤4
x
1
,x
2
≥0
3.1 Solve the Linear programming problem using the simplex method. 3.2 Construct the dual linear programming problem for the primal problem. 3.3 By using the optimal simplex tableau of the primal problem determine the solution of the dual problem.
Answers
To solve the linear programming problem using the simplex method, we first convert the problem into standard form.
The original problem: Maximize z = -x₁ + 3x₂; subject to: x₁ + 3x₂ ≤ 5; -x₁ + x₂ ≤ 1 ; x₁ + x₂ ≤ 4; x₁, x₂ ≥ 0. The problem in standard form: Maximize z = -x₁ + 3x₂, subject to: x₁ + 3x₂ + x₃ = 5; -x₁ + x₂ + x₄ = 1; x₁ + x₂ + x₅ = 4; x₁, x₂, x₃, x₄, x₅ ≥ 0. Using the simplex method, we perform the iterations to find the optimal solution. Starting with the initial basic feasible solution, we pivot until we reach an optimal solution. The optimal solution is found when all coefficients in the objective row are non-negative. The final optimal solution obtained by the simplex method is: x₁ = 0; x₂ = 1; z = 3. To construct the dual linear programming problem, we use the coefficients from the constraints of the primal problem as the objective coefficients in the dual problem.
The variables in the primal problem become the constraints in the dual problem, and the constraints in the primal problem become the variables in the dual problem. The dual problem for the given primal problem is: Minimize w = 5y₁ + y₂ + 4y₃, subject to: y₁ - y₂ + y₃ ≥ -1; 3y₁ + y₂ + y₃ ≥ 3. Using the optimal simplex tableau of the primal problem, we can determine the solution of the dual problem. The optimal tableau will provide us with the values of the primal variables and the dual variables. In this case, the primal variables are x₁ and x₂, and the dual variables are y₁, y₂, and y₃. From the optimal simplex tableau, we find that x₁ = 0, x₂ = 1, y₁ = 1, y₂ = 0, and y₃ = 0. These values give the solution to the dual problem. The minimum value of the dual objective function w is obtained as w = 5(1) + 0 + 4(0) = 5.
To learn more about linear programming click here: brainly.com/question/14309521
#SPJ11
What is the value of StartFraction 1 Over 6 Superscript 0 EndFraction
Answers
The value of the expression \((1/6)^0\) is 1.
What is a fraction?A fraction is written in the form of a numerator and a denominator where the denominator is greater that the numerator.
Example: 1/2, 1/3 is a fraction.
We have,
\((1/6)^0\)
Anything to the power zero is always 1.
Thus,
The value is 1.
Learn more about fractions here:
https://brainly.com/question/24370499
#SPJ1
After driving
three hours, the Factors
stopped for lunch. The bill for 4
hamburgers and 4 milkshakes was
$12.65. How much change did Ms.
Factor receive from a $20 bill?
Answers
Answer:
7.35
Step-by-step explanation:
I Need Help With This Question

Answers
Answer:
Step-by-step explanation:
Dont do it. Just take the detention
ABC OR D PLEASE HELP

Answers
C I think not 100 percent sure
write a solution system for the inequality 3x-2>10
Answers
Answer:
x>4
Step-by-step explanation:
3x - 2 >10 add 2 to both sides
3x > 12 Divide both sides by 3
x >4
Answer:
\(x > \bf 4\)
Step-by-step explanation:
To find a solution to this inequality, we have to rearrange this equation to make \(x\) its subject:
\(3x - 2 > 10\)
⇒ \(3x - 2 + 2 > 10 + 2\) [Add 2 to both sides]
⇒ \(3x > 12\)
⇒ \(\frac{3x}{3} > \frac{12}{3}\) [Divide both sides by 3]
⇒ \(x > \bf 4\)
pls help
Solve x²-64 = 0.
1. Isolate x²: x² = 64
2. Apply the square root property of equality: √x²= √64
3. Isolate the variable:
X=
T
x =

Answers
Explanation:
We simplify the square root of 64 to get 8
\(\sqrt{64} = \sqrt{8^2} = 8\)
Then we'll have the plus minus out front to say
\(x = \pm \sqrt{64} = \pm 8\)
That breaks down into x = 8 or x = -8
As a check
x^2 = (8)^2 = 8*8 = 64
x^2 = (-8)^2 = (-8)*(-8) = 64
Both values lead to 64 when squaring.
8(7n+3)=24+7n
no solution solution and infinitely many solutions?
Answers
Answer:
Step-by-step explanation:
56n+24 = 24 + 7n
49n + 24 = 24
49n = 0
n = 0
solution
Answer:
n = 0
Step-by-step explanation:
8(7n + 3) = 24 +7n
1. distribute the 8 inside the paranthesis
56n + 24 = 24 + 7n
2. subtract 24 from both sides
56n = 7n
3. subtract 7n from both sides
49n = 0
n = 0
hey if anyone understands do you you think you could help i'm struggling a little bit :(

Answers
Answer:
2x=18
x=9
Step-by-step explanation:
So, to start you subtract 12 from 30 to get 18.
then 18 divided by x gives you 9
so X=9
Answer:
2x = 18 and x = 9
Step-by-step explanation:
i've done it before so i know its right
can some one help me

Answers
Answer:
84 grams and 5 ounces
Step-by-step explanation:
because one ounce equals 28 grams, that means 3 ounces = 3 * 28 = 84
because 28 grams equals 1 ounce, 140 grams = 140 / 28 = 5 ounces
grace was born in 1995. how old will she be in 2027
Answers
Answer:
12
Step-by-step explanation:
2007 - 1995
Which three angle measures can be used to make ΔABC? Responses A 71°71° B 36°36° C 41°41° D 88°88° E 68°
Answers
The angles that can be used to make ΔABC are 71°, 41° and 68°
In this question, we have been given some angles.
A 71°71°
B 36°36°
C 41°41°
D 88°88°
E 68°
We need to find angles that can be used to make ΔABC.
We know that the sum of all angles of triangle is 180°
We need to find three angles whose sum is 180°
71° + 41° + 68° = 180°
Since the sum of angles 71°, 41° and 68° is 180°, we can use these angles to make ΔABC
Therefore, the angles that can be used to make ΔABC are 71°, 41° and 68°
Learn more about the triangle here:
https://brainly.com/question/22469440
#SPJ1