Answers
Answer:y<3/4x
Step-by-step explanation:
Its proportional
y intercept is 0 which means nothing
slope is 3/4
so
y<3/4x
BTW dotted lines are < not ≤
Related Questions
Alice,barbra, and carol are sisters. alice is 3 years younger then barbara is 5 years younger then carol. together the sisters are 68 years old. how old is barbara?
Answers
The age of Barbra is 22 years.
What is method of substitution?The algebraic method for solving simultaneous linear equations is the substitution method. A quantity of one variable through one expression is replaced in the second equation, as the name implies.
Now, according to the question.
Let 'a' be the age of Alice.
Let 'b' be the age of Barbra
Let 'c' be the age of Carol.
The sum of age of all three sisters is 68 years.
Thus, a + b + c = 68
Now, as Alice is three years younger than Barbra.
a = b - 3
and, Barbra is 5 years younger than Carol.
b = c - 5
c = b + 5
By substitution of values of a and c in total age.
(b - 3) + b + (b + 5) = 68
3b - 3 + 5 = 68
On solving the expression.
b = 22
Therefore, the age of Barbra is 22 years.
To know more about the method of substitution, here
https://brainly.com/question/26094713
#SPJ4
which proportion could you use to convert 4 meters to millimeters
Answers
A jar of crunctiy poanut Buller eoriains 1.31 kg of poskut buttes, if yos use 7.85 of the pearet tuther for a sahtwich, how many ounces of pessit butter ded you take cut of the container? Expeess your antwer to two signifieant figures.
Answers
You took out approximately 3.63 ounces of peanut butter from the container.
To calculate the amount of peanut butter taken out of the container, we need to determine the weight of the pear butter used for the sandwich.
Given that the jar contains 1.31 kg of peanut butter and you used 7.85% of the peanut butter for the sandwich, we can calculate the weight of the peanut butter used as follows:
Weight of peanut butter used = 1.31 kg × 7.85% = 0.103 kg
To convert the weight from kilograms to ounces, we can use the conversion factor: 1 kg = 35.27396 ounces.
Weight of peanut butter used = 0.103 kg × 35.27396 ounces/kg ≈ 3.638 ounces
Therefore, you took out approximately 3.638 ounces of peanut butter from the container. Rounded to two significant figures, the amount is approximately 3.63 ounces.
To know more about calculating weights and converting units, refer here:
https://brainly.com/question/11503856#
#SPJ11
Which is a true statement about the number 1?
1. One is a factor of every whole number since every number is divisible by itself.
2. One is not a factor of any number because it is neither a prime number nor a composite number.
3. One is a prime number because it has less than two factors.
4. One is a composite number because it has more than two factors.
Answers
Answer:
Answer 1 is correct.
Step-by-step explanation:
As Answer 1 states, "One is a factor of every whole number since every number is divisible by itself." This is because every number can be divided by 1 without leaving a remainder, making it a factor of all whole numbers.
LN is tangent to circle O at point M and QM is a diameter. Determine the measure of the following angles. The measure of ∠QML is degrees. The measure of ∠PMN is degrees
Answers
LN is tangent to circle O at point M and QM is a diameter. The measure of ∠QML and ∠PMN are 90° and 63° respectively.
1) To Determine the degree measurement of ∠QML
Based on the Perpendicular Tangent Theorem, tangent lines are always perpendicular to a circle's radius at the point of intersection
So, the radius OM is perpendicular to line LN at point M.
Hence,
The value of ∠QML = 90°
2) To determine the degree measurement of angle PMN
∠QMN = ∠QMP + ∠PMN
By the angle addition postulate, we can calculate this measurement as follows:
∠QMN = 90°
∠QMP = 27°
Replace with and substitute the value of angle QML into the equation.
90° = 27° + ∠PMN
∠PMN = 90° - 27° = 63°
Therefore, the value of ∠PMN is 63°
Learn more about perpendicular tangent theorem here brainly.com/question/30306156
#SPJ4
A cone with a fixed height of 18 cm is shown on a computer screen. An animator increases the radius r at a rate of 2 cm per minute. Write the function that gives the volume v(r) of the cone as a function of time f(t). Assume the radius is 2 cm at t=1.
Answers
Answer:
18.2=36
2.18+38=98
Step-by-step explanation:
The function that gives the volume v(r) of the cone when the height of 18 cm as a function of time is \(24 \pi + 48\pi t + 24\pi t^2\).
Given that:
The height of the cone = 18 cm
The radius of the cone's base at a rate of = 2 cm.
The radius r increases at a rate of 2 cm per minute,
At t = 1,
The radius will be r = 2+ 2t
The volume of the cone is given by \(\dfrac{1}{3} \pi r^3\).
V = \(\dfrac{1}{3} \pi r^3 h\)
= \(\dfrac{1}{3} \pi (2+ 2t)^2(18)\)
= 6\pi (4+ 8t+4t^2)
= \(24 \pi + 48\pi t + 24\pi t^2\)
The function that gives the volume v(r) of the cone as a function of time is \(24 \pi + 48\pi t + 24\pi t^2\).
Learn more about volume here:
https://brainly.com/question/28338582
#SPJ3
Susan’s science class is performing an experiment that involves dropping objects from various heights, starting close to the ground and working upward to 8 feet. The function , where x represents the distance from the ground, represents the time it takes for the object Susan drops to hit the ground. The graph represents the function
Identify some of the key features of the graph. That is, determine if the function is monotonically increasing or decreasing, state the end behavior, find the x- and y-intercepts, find the endpoint, and state the domain and the range of the graph (without considering the context).

Answers
Answer:
1) The function is monotonically increasing
2) The end behavior of the function is x tends to infinity as t(x) tends infinity
3) The x and y -intercept is (0, 0)
4) The endpoint is (0, 0)
5) The domain is 0 ≤ x ≤ +∞
The range is 0 ≤ t(x) ≤ +∞
Step-by-step explanation:
1) The given function of the time for the object to hit the ground is t(x) = 1/4·√x
Where;
x = The distance from the ground
t = The time it takes for the object to hit the ground
Monotonically increasing function, we have;
A function that is continuous on [a, b] and it can be differentiated in the domain, (a, b) is monotonically increasing when df(x)/dx > 0 for all values of x in (a, b)
However, where df(x)/dx < 0 for all values of x in (a, b), the function is decreasing
Therefore, using an online tool, we have;
dt(x)/dx = d(1/4·√x)/dx = 1/8 × 1/√x
Therefore, the dt(x)/dx > 0, for 0 < x < +∞ and the function is monotonically increasing
2) The end behavior of the function as x tends to infinity, t(x) = 1/4·√x approaches infinity
3) From the end behavior, and the nature, of the function t(x) = 1/4·√x, where both variables are directly proportional, we have that the x and y -intercept = (0, 0)
4) The endpoint is (0, 0) given that as t(x) tends to 0, x tends to 0
5) The domain is 0 ≤ x ≤ +∞
The range is 0 ≤ t(x) ≤ +∞.
Answer:
The function is monotonically increasing since the output values are continually getting larger. This also tells us that the end behavior of the function is infinity.
The x-intercept is (0,0), the y-intercept is (0,0), and the endpoint too is (0,0).
The domain of the graph is all values greater than or equal to 0, and the range is all positive output values.
Step-by-step explanation:
Find the radius of Circle N.

Answers
Answer:
C = 113.04
Step-by-step explanation:
arc ACB = (Ф/360) * 2πr
81.64 = (260/360) * 2 * π * r
r = (81.64 * 360)
2 * π
r = 17.99 cm
Circumference = 2 * π * r
C = 2 * π * 17.99
C = 113.04
I need the answer to this

Answers
Answer:
y = 6.5
Step-by-step explanation:

Determine the independent and dependent variable from the following situation. Delilah was given $50 for her birthday. Every month she saves $15.
independent variable is?
dependent variable is?
Answers
In the given situation:
The independent variable is: Time or months. Delilah's saving and accumulation of money depend on the passage of time.
The dependent variable is: Amount of money saved. The amount of money Delilah has saved is dependent on the number of months that have passed and her consistent savings of $15 each month.\(\)
I HAVE 5 MINS PLZ HELP!

Answers
it’s positive because it’s going up
aight can you guys help, it’s a one-step equation and i’m smol brain, and can you give me a step-by-step cuz i forgot how to do it, thank youuuuu<3

Answers
Answer:
16
Step-by-step explanation:
The variable a minus 10 equals 6. If you substituted a for 16, and subtracted 10, you'd get 6. Substituting the rest of the numbers and subtracting 10 wouldn't give you 6.
in order to find a, you want to get a alone by itself.
to do that you add 10 to both sides because it can never be just one side
then that will give you a= 10 + 6
which is then a = 16
so your answer is 16
now say you sample 10 independent customers. what is the probability that less than or equal to 5 (five) of them will take more than 3 minutes to check out their groceries? round to the nearest hundredths/second decimal place,
Answers
The probability that less than or equal to 5 of the 10 independent customers will take more than 3 minutes to check out their groceries is approximately 0.9245.
To calculate this probability, we can use the binomial probability formula. Let's denote X as the number of customers taking more than 3 minutes to check out. We want to find P(X ≤ 5) when n = 10 (number of trials) and p (probability of success) is not given explicitly.
Step 1: Determine the probability of success (p).
Since the probability of each customer taking more than 3 minutes is not provided, we need to make an assumption or use historical data. Let's assume that the probability of a customer taking more than 3 minutes is 0.2.
Step 2: Calculate the probability of X ≤ 5.
Using the binomial probability formula, we can calculate the cumulative probability:
P(X ≤ 5) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5)
P(X ≤ 5) = C(10, 0) * p^0 * (1 - p)^(10 - 0) + C(10, 1) * p^1 * (1 - p)^(10 - 1) + C(10, 2) * p^2 * (1 - p)^(10 - 2) + C(10, 3) * p^3 * (1 - p)^(10 - 3) + C(10, 4) * p^4 * (1 - p)^(10 - 4) + C(10, 5) * p^5 * (1 - p)^(10 - 5)
Substituting p = 0.2 into the formula and performing the calculations:
P(X ≤ 5) ≈ 0.1074 + 0.2686 + 0.3020 + 0.2013 + 0.0889 + 0.0246
P(X ≤ 5) ≈ 0.9928
Rounding this probability to the nearest hundredth/second decimal place, we get approximately 0.99. However, the question asks for the probability that less than or equal to 5 customers take more than 3 minutes, so we subtract the probability of all 10 customers taking more than 3 minutes from 1:
P(X ≤ 5) = 1 - P(X = 10)
P(X ≤ 5) ≈ 1 - 0.9928
P(X ≤ 5) ≈ 0.0072
Therefore, the probability that less than or equal to 5 customers out of 10 will take more than 3 minutes to check out their groceries is approximately 0.0072 or 0.72%.
For more questions like Probability click the link below:
https://brainly.com/question/11234923
#SPJ11
A particle (charge = +40 uc) is located on the x axis at the point x = -20 cm, and a second particle (charge = -50 uc) is placed on the x axis at x = +30 cm. What is the magnitude of the total electrostatic force on a third particle (charge = -4. 0 uc) placed at the origin (x = 0)?.
Answers
The total electrostatic force on the third particle will be 56 N in -x direction.
q1 = +40 μC, x1 = -20 cm = - 0.2 m
q2 = -50 μC, x2 = 30 cm = 0.3 m
q = -4 μC, x = 0
We know that, the electrostatic force between two charges
F = kQ1Q2/d²
k = 9 × 10⁹ Nm²/C²
here, d: distance between two charges
F1 = k(40×10⁻⁶)(-4× 10⁻⁶)/(0.2)²
F1 = - 36 N {(-) sign shows the force is attraction force}
so, the direction of F1 on q is -x-direction
F2 = k(-50×10⁻⁶)(-4× 10⁻⁶)/(0.3)²
F2 = 20 N {Repulsive force because both particles are having negative charge}
so, the direction of F2 on q is in the -x-direction
So Total force F = F1+F2 = 20+36 = 56 N
Therefore, the total electrostatic force on the third particle will be 56 N in the -x direction.
#SPJ4
To learn more about electrostatic force:
https://brainly.com/question/17692887
Let abcdef be a convex hexagon. let a', b', c', d', e', f' be the centroids of triangles fab, abc, bcd, cde, def, efa, respectively.
(a) show that every pair of opposite sides in hexagon a'b'c'd'e'f' (namely a'b' and d'e', b'c' and e'f', and c'd' and f'a') are parallel and equal in length.
(b) show that triangles a'c'e' and b'd'f' have equal areas.
Answers
(a) shows that every pair of opposite sides in the hexagon a′b′c′d′e′f′ are parallel and equal in length. On the other hand, (b) demonstrates that the triangles a′c′e′ and b′d′f′ have equal areas.
(a) To show that every pair of opposite sides in hexagon a'b'c'd'e'f' are parallel and equal in length, we can use the fact that the centroids of triangles divide the medians into segments of equal length.
Let's consider a'b' and d'e'. The centroid of triangle fab, a', divides the median fb into two segments, a'f and a'b', such that a'f = 2/3 * fb. Similarly, the centroid of triangle def, e', divides the median de into two segments, e'd and e'f', such that e'd = 2/3 * de.
Since fb = de (opposite sides of hexagon abcdef), we have a'f = e'd. Now, we can consider the triangles a'f'd' and e'df'. By the properties of triangles, we know that if two sides of a triangle are equal, and the included angles are equal, then the triangles are congruent.
In this case, a'f' = e'd' (as shown above) and angle a'f'd' = angle e'df' (corresponding angles). Therefore, triangle a'f'd' is congruent to triangle e'df'.
By congruence, the corresponding sides a'd' and e'f' are equal in length.
By similar reasoning, we can show that b'c' and e'f', as well as c'd' and f'a', are parallel and equal in length.
(b) To show that triangles a'c'e' and b'd'f' have equal areas, we can use the fact that the area of a triangle is one-half the product of its base and height.
In triangle a'c'e', the base is c'e' and the height is the perpendicular distance from a' to c'e'. Similarly, in triangle b'd'f', the base is d'f' and the height is the perpendicular distance from b' to d'f'.
Since opposite sides in hexagon a'b'c'd'e'f' are parallel (as shown in part (a)), the perpendicular distance from a' to c'e' is equal to the perpendicular distance from b' to d'f'.
Therefore, the heights of triangles a'c'e' and b'd'f' are equal. Additionally, the bases c'e' and d'f' are equal (as shown in part (a)).
Using the area formula, area = 1/2 * base * height, we can see that the areas of triangles a'c'e' and b'd'f' are equal.
Hence, we have shown that triangles a'c'e' and b'd'f' have equal areas.
Learn more about centroid here https://brainly.com/question/29148732
#SPJ11
Solve for x.
A) 4
C) 1
B) 10
D) 12

Answers
Answer:
A) 4
Step-by-step explanation:
3*4 = 12
1+12=13
How do I find the area of a triangle in a coordinate plane
Answers
Can someone help me with this? Thanks.

Answers
Answer:
7.38461538462
Step-by-step explanation:
1/2x6/5=3.25
24/3.25=7.38461538462
Answer:
A. b = \(\frac{2a}{a}\)
B. b = 40
Step-by-step explanation:
mark brainliest pls
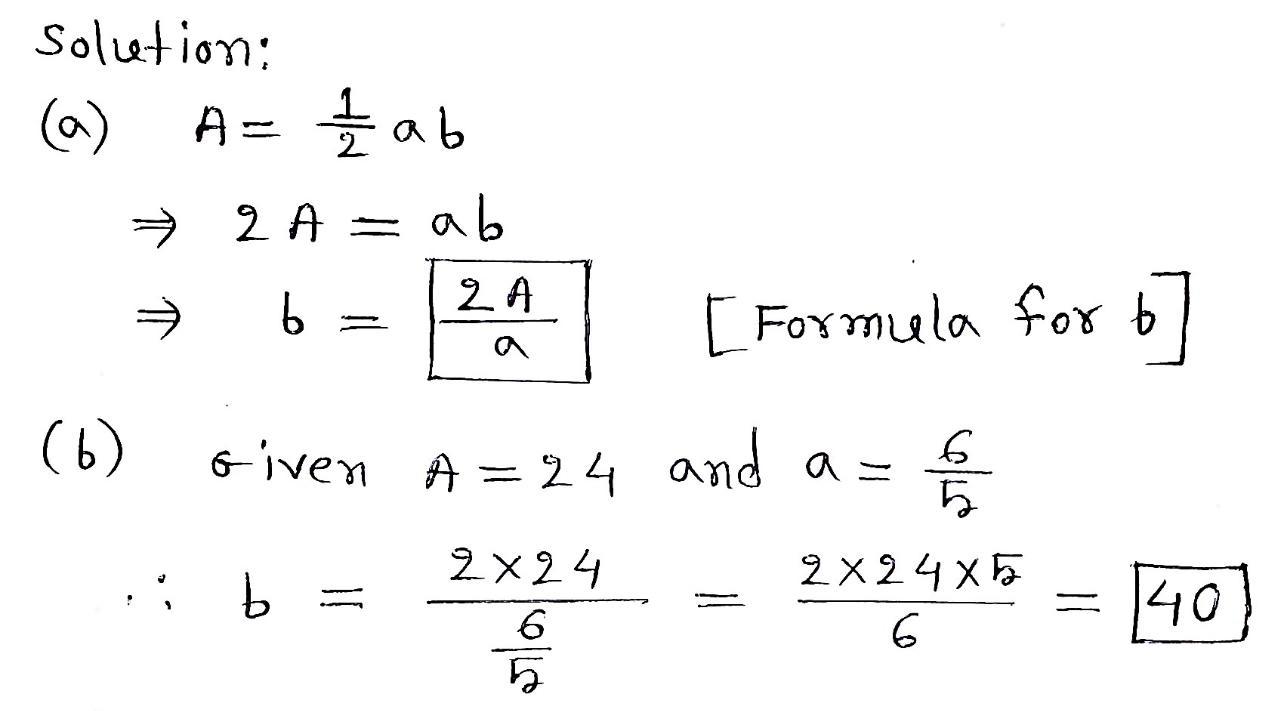
The actual distance between two cities is 35 miles. The scale on a map uses 2 inches to represent 5 miles.How many inches apart are the two cities on the map?
A: 3.5 in
Answers
Answer:
14 inches.
Step-by-step explanation:
Answer:
35 miles divided into 1 inch is equal to 7 and 7 divided by 2 equals 3 5 inches.
WELKAS30
Will give brainilest HELP ASAP

Answers
The value of the expression is 8.37a + 16.11
What is algebraic expression?An algebraic expression is an expression built up from constant algebraic numbers, variables, and the algebraic operations (addition, subtraction, multiplication, division and exponentiation by an exponent that is a rational number
The given expression is
(8.95 + 5a) + (7.16 + 3.37a)
5a+3.37a +8.95 + 7.16
8.37a + 16.11
Learn more about algebraic expression on https://brainly.com/question/24479484
#SPJ1
If they exist, find two numbers whose sum is 100 and whose product is a minimum. If such two numbers do not exist, explain why.
Second Derivative Test:
If f is a function defined on an interval I and f is twice differentiable function, then for critical value x
=
c
,
If f
′
(
c
)
=
0
and
f
′′
(
c
)
<
0
, then f
(
c
)
gives maximum value of f.
If f
′
(
c
)
=
0
and
f
′′
(
c
)
>
0
, then f
(
c
)
gives minimum value of f.
Answers
The two numbers whose sum is 100 and whose product is a minimum are: x= 50 and y= 50.
To find two numbers whose sum is 100 and whose product is a minimum, we can use the Second Derivative Test. Let's start by defining the two numbers as x and y. We know that:
x + y = 100
We want to find the minimum value of xy. So, let's define a function f(x) = xy. We can rewrite this function in terms of one variable:
f(x) = x(100 - x) = 100x - x^2
Now, let's find the critical point of this function by taking the derivative:
f'(x) = 100 - 2x
Setting f'(x) = 0 to find the critical point:
100 - 2x = 0
x = 50
So, the critical point is x = 50. To determine whether this is a minimum or maximum, we need to find the second derivative:
f''(x) = -2
Since f''(50) < 0, we know that the critical point x = 50 is a maximum. Therefore, to find the minimum value of f(x), we need to evaluate f at the endpoints of the interval [0, 100]:
f(0) = 0
f(100) = 0
Since f(x) is decreasing from x = 0 to x = 50, and increasing from x = 50 to x = 100, the minimum value of f(x) occurs at x = 50. Therefore, the two numbers whose sum is 100 and whose product is a minimum are:
x = 50
y = 100 - x = 50
So, the two numbers are 50 and 50.
To know more about Second Derivative Test, refer to the link below:
https://brainly.com/question/30404403#
#SPJ11
Two ferries start moving towards each other from shores A and B. When they pass each other for the first time the distance to shore B is 100 meters. Once they reach their destinations and start traveling back at the same time. When they meet for the second time, the distance to shore A is 50 meters. What is the distance between the shores A and B? HELP will give brainliest! Its not 150 or 1700
Answers
The distance between the shores A and B is 250 meters.
Distance between shore A and BWidth of the river= D
Distance covered by boat A and B= a and b
Distance covered by A and B =Width of the river for the first meet.
D = a + b..............(1)
Hence:
b = 100 meters.............(2)
Sum of the distances traveled is 3times with width of the river as they both went 3 times after they first passed.
Second time= 50 meters
Hence:
3a = D+ 50...........(3)
Put the value of equation 2 into equation 1
3 ×100 = D+ 50
D=300-50
D =250 meters
Therefore the distance between the shores A and B is 250 meters.
Learn more about distance between the shores A and B here:https://brainly.com/question/14763249
#SPJ1
Reid is a novice cook trying to perfect his baked potato recipe. He decides to put many potatoes in the oven and invites all his friends over. Every few minutes he takes a potato out of the oven and asks some friends to rate its taste on a scale from 1 to 10, where 10 is excellent. For each taste, Reid writes down the number of minutes the potato spent in the oven, x, as well as its rating from 1 to 10, y. The least squares regression line of this data set is:
y=0. 009x+3. 43
Answers
The least squares regression line predicts a 0.534 increase in score for each minute the potatoes are in the oven.
If the data shows a weak relationship between two variables, the line that best fits this linear relationship is called a least-squares regression line, and it minimizes the vertical distance of the data points from the regression line. The term "least squares" is used because it is the minimum of the sum of squared errors, also known as "variance".
In a regression analysis, the dependent variable is shown on the vertical y-axis and the independent variable is shown on the horizontal x-axis. These specifications form the equation for the line of best fit, determined by least squares.
According to the Question:
Reid notes the x number of minutes the potatoes were in the oven and a y rating from 1 to 10. The least squares regression line for this data set is:
y = 0. 009x+3. 43
For each additional minutes a potatoes spends in the oven, then the least square regression line predicts its rating will increase by 0.534.
Learn more about regression line:
https://brainly.com/question/19724978
#SPJ4
what two requirements do you need for the chi square goodness of fit test
Answers
Answer:
Data values that are a simple random sample from the full population.
Categorical or nominal data. The Chi-square goodness of fit test is not appropriate for continuous data.
A data set that is large enough so that at least five values are expected in each of the observed data categories.
please help version 2

Answers
Answer:
16°
Step-by-step explanation:
2x° + 6° = 38°
x° = (38°- 6°)÷2=16°
2x + x + 12 + 96 = 180, What is x?
Answers
Answer:
X = 24
Step-by-step explanation:
2x + x + 12 + 96 = 180
combine like terms
3x + 108 = 180
subtract 108
3x = 72
divide by 3
x = 24
Hope this helps. Pls give brainliest.
3(2f + 4) = 2(3f - 6)
Answers
Answer:
I would say no solution
Step-by-step explanation:
There are no values of the variable that make the equation true.
Answer:
no solution
Step-by-step explanation:
0=-24 at the end, which leads to no solution because 0 does not equal -24
Please solve. Thank you

Answers
.
• Multiple 68 by 41
Your answer would be 2,788
That's your answer.
HELP MEEEEEEEEEEEEEEEEEE

Answers
Answer:
\( - 8 {x}^{2} - x - 4\)
Step-by-step explanation:
Let's subtract:
\(( - 8 {x}^{2} - 8) - (x - 4)\)
\( - 8 {x}^{2} - 8 - x + 4\)
\( - 8 {x}^{2} - x - 4\)
complementary and supplementary (geometry)
Answers
Answer:
Complementary angles add up to 90 degrees and Supplementary angles add up to 180 degrees.
Hope this helps!
