The probability of a high school basketball team winning any game is 58%. This team is in a six-game tournament,
and the games are played independently of one another. Let X represent the number of games the team might win
in this tournament. What are the mean and standard deviation of X?
Answers
The mean (expected value) of X is 3.48, and the standard deviation of X is 1.27.
Basketball Game Win StatsMean (Expected Value) of X:The mean or expected value of X, representing the number of games the team might win, can be calculated using the formula:
E(X) = n * p
where:
n = number of games (6)
p = probability of winning each game (0.58)
So, E(X) = 6 * 0.58 = 3.48
Standard Deviation of X:The standard deviation of X, representing the spread of the distribution, can be calculated using the formula:
SD(X) = √(n * p * (1 - p))
where:
n = number of games (6)
p = probability of winning each game (0.58)
So, SD(X) = √(6 * 0.58 * (1 - 0.58)) = 1.27
Therefore, the mean of X is 3.48, and the standard deviation of X is 1.27.
Learn more about Basketball Game Win Stats here:
https://brainly.com/question/13899096
#SPJ4
Related Questions
an expoenetial function g models a relationship in which the dependent variable is multiplied by 2.5 for every 1 unit the independent variable x increases. the value of the function 0 is 8
Answers
The exponential function that models the relationship is:
g(x) = 8 * (2.5)^x
To model the relationship described, we can write the exponential function as:
g(x) = a * b^x
Given that the dependent variable is multiplied by 2.5 for every 1 unit increase in the independent variable, we have:
2.5 = b^1
Solving for b, we find that b = 2.5.
Now, we can substitute the value of x = 0 into the equation and solve for a:
8 = a * (2.5)^0
8 = a * 1
a = 8
Know more about exponential function here:
https://brainly.com/question/14355665
#SPJ11
a large pile of coins consists of pennies, nickels, dimes, and quarters (at least 16 of each). how many different collections of 16 coins can be chosen? [a] how many different collections of 16 coins chosen at random will contain at least 3 coins of each type?
Answers
the size of the union of the three sets is: |A ∪ B ∪ C| = |A| + |B| + |C| - |A ∩ B| - |A ∩ C| - |B ∩ C| + |A ∩ B ∩ C| = 3 × 24 million - 3 × 1.4 million + 1.2 million ≈ 69 million
A combination is a way of selecting a subset of objects from a larger set without regard to their order. The formula for the number of combinations of n objects taken r at a time is:
C(n, r) = n! / (r! × (n - r)!)
where n! means the factorial of n, which is the product of all positive integers up to n. For example, 5! = 5 × 4 × 3 × 2 × 1 = 120.
To apply this formula to our problem, we first need to count the total number of coins in the pile. Since there are at least 16 of each type, the minimum total is:
16 + 16 + 16 + 16 = 64
But there could be more coins of each type, so the total could be larger than 64. However, we don't need to know the exact number, only that it is large enough to allow us to choose 16 coins from it.
Using the formula for combinations, we can calculate the number of different collections of 16 coins that can be chosen from the pile:
C(64, 16) = 64! / (16! × (64 - 16)!) ≈ 1.1 billion
That's a very large number! It means there are over a billion ways to choose 16 coins from a pile that contains at least 16 of each type.
To answer the second part of the question, we need to count the number of collections that contain at least 3 coins of each type. One way to do this is to use the inclusion-exclusion principle, which says that the number of elements in the union of two or more sets is equal to the sum of their individual sizes minus the sizes of their intersections, plus the sizes of the intersections of all possible pairs, minus the size of the intersection of all three sets, and so on.
In this case, we can consider three sets:
- A: collections with at least 3 pennies
- B: collections with at least 3 nickels
- C: collections with at least 3 dimes
- D: collections with at least 3 quarters
The size of each set can be calculated using combinations:
|A| = C(48, 13) ≈ 24 million
|B| = C(48, 13) ≈ 24 million
|C| = C(48, 13) ≈ 24 million
|D| = C(48, 13) ≈ 24 million
Note that we have to choose 3 coins of each type first, leaving 4 coins to be chosen from the remaining 48 coins.
The size of the intersection of any two sets can be calculated similarly:
|A ∩ B| = C(43, 10) ≈ 1.4 million
|A ∩ C| = C(43, 10) ≈ 1.4 million
|A ∩ D| = C(43, 10) ≈ 1.4 million
|B ∩ C| = C(43, 10) ≈ 1.4 million
|B ∩ D| = C(43, 10) ≈ 1.4 million
|C ∩ D| = C(43, 10) ≈ 1.4 million
Note that we have to choose 3 coins of each type first, leaving 1 coin to be chosen from the remaining 43 coins.
The size of the intersection of all three sets can also be calculated:
|A ∩ B ∩ C| = C(38, 7) ≈ 1.2 million
Note that we have to choose 3 coins of each type first, leaving 1 coin to be chosen from the remaining 38 coins.
learn more about intersection here:
https://brainly.com/question/12089275
#SPJ11
plz help assap!!!!!!

Answers
Answer:
3y = 60°, 2y = 40° , 4x = 104°, x = 26°, y = 50°
Step-by-step explanation:
Triangle g
180° = 80° + 3y + 2y
100° = 5y
y = 20°
Triangle h
y = 180° - 130°
y = 50°
180° = 4x + x + 50°
130° = 5x
x = 130 / 5
x = 26°
How would you make 350 mL of a buffer with a total concentration of 0.75M and a pH of 9.00 from the list of materials below? (your answer should include the volumes of two solutions and the amount of DI water needed to reach the total volume) [remember: vol*total conc->total moles->moles weak, targetpH->ratio->stoich->moles strong] i. A solution of 1.25M hydrochloric acid ii. A solution of 1.25M sodium hydroxide iii. A solution of 1.25M chloroacetic acid (pKa=2.85) iv. A solution of 1.25M ammonia (pKa=9.25) v. A solution of 1.25M carbonic acid (pK_a1=6.37,pK_a2=10.32)
vi. A solution of 1.25M acetic acid( pKa=4.75) 1) What would be the volume of weak component and what would be the volume of strong component?
Answers
Volume = 28.16 mL of weak component and volume of strong component.
For creating 350 mL of a buffer with a total concentration of 0.75 M and a pH of 9.00 from the given materials, the steps required are as follows:
Step 1: Calculate the pKa of the weak acid present in the solution. The pH of the buffer is equal to the pKa plus the log of the ratio of conjugate base to weak acid in the buffer. Thus, for the pH of 9.00, the pKa would be 4.75 (acetic acid) for a weak acid or 9.25 (ammonia) for a weak base.
Step 2: Determine the volumes of the weak and strong components. In this case, the weak component can be acetic acid or ammonia, and the strong component can be NaOH or HCl. The total concentration of the buffer is 0.75 M, and a total volume of 350 mL is required. Thus, the moles of buffer required would be:
Total moles of buffer = Molarity × Volume of buffer
Total moles of buffer = 0.75 × (350/1000)
Total moles of buffer = 0.2625 Moles
Step 3: Determine the amount of moles of weak acid/base and strong acid/base. If the weak component is acetic acid, the ratio of the conjugate base to weak acid required for a pH of 9.00 would be:
Ratio = (10^(pH−pKa))
Ratio = 10^(9−4.75)
Ratio = 5623.413
The moles of the weak component required would be:
Total moles of weak component = (0.2625) / (Ratio + 1)
Total moles of weak component = (0.2625) / (5623.413 + 1)
Total moles of weak component = 4.662 × 10^-5 Moles
The moles of the strong component required would be:
Moles of strong component = (0.2625) - (0.00004662)
Moles of strong component = 0.2624 Moles
Acetic acid (CH3COOH) is a weak acid, which means it can donate H+ ions to water and thus decrease the pH of a solution. Thus, we need to add a weak base, which in this case is ammonia (NH3), as it can accept H+ ions and increase the pH. The pKa of ammonia is 9.25. Thus, we can use the Henderson-Hasselbalch equation to determine the amount of ammonia required to prepare the buffer solution.
pH = pKa + log ([A-] / [HA])
9.00 = 9.25 + log ([NH4+] / [NH3])
log ([NH4+] / [NH3]) = -0.25
([NH4+] / [NH3]) = 0.56
So the ratio of ammonia (weak base) to ammonium chloride (strong acid) would be 0.56. This means that if we add 0.56 moles of ammonia, we would require 0.56 moles of ammonium chloride to make the buffer. The volume of 1.25 M ammonia solution required would be:
Volume = (0.56 × 63) / 1.25
Volume = 28.16 mL
The volume of 1.25 M ammonium chloride solution required would be:
Volume = (0.56 × 63) / 1.25
Volume = 28.16 mL
Learn more about acid buffer:
brainly.com/question/17350370
#SPJ11
Gary Foshee created a popular probability puzzle that goes like this: "I have two children. One is a boy born on a Tuesday.
What is the probability I have two boys?"
In this puzzle, knowing that one of Gary's children was born on a Tuesday is as important as knowing that he has one boy.
Assuming that having boys and girls are equally likely and that births are equally likely on every day of the week, what is the
probability that Gary has two boys, given the available information? (Hint: When Gary said that one is a boy born on a
Tuesday, he meant at least one child is a boy born on a Tuesday. )
a
Answers
The answer is 1/3.
Richard shares a variation (imagined by Gary Foshee) which it find the counter-intuitive: “I have two children. One is a boy born on a Tuesday. What is the probability I have two boys?” (Assume uniformity over genders and days of the week.) This is easy to solve, using the method of your choice (1, 2).
The probability that Gary Foshee has two boys, given that one of them is a boy born on a Tuesday, is approximately 0.481 or 48.1%.
Explanation:The problem you're dealing with is a classic problem in probability theory. Given the conditions of equal likelihood for boys and girls and equal likelihood for births on any day of the week, we can proceed as follows:
First, it's important to understand total numbers of outcomes. Considering the genders (2 possible) and days of the week (7 possible) for two children, we end up with 2*7*2*7= 196 possible combinations.
Next, consider the number of outcomes where at least one child is a boy born on a Tuesday. This includes scenarios where either the first or second child is the boy born on a Tuesday, but not both. Therefore, the total would be 2*7*1*1 + 1*1*2*7 - 1*1*1*1 = 27 scenarios (subtracting the one scenario where both children are boys born on Tuesday).
Finally, we're interested in the scenarios where the other child is also a boy. Given our condition of at least one boy born on a Tuesday, this means scenarios where the other child is a boy on any day of the week. This gives 7+6 scenarios (including situations where both boys are born on a Tuesday, and where the other boy is born on any other day of the week).
Therefore, the probability of the other child being a boy, given at least one boy born on Tuesday, equals 13/27 ≈ 0.481.
Learn more about Probability here:https://brainly.com/question/22962752
#SPJ2
\(3 tan x -\sqrt{3} = 0\)
Please give a step-by-step answer
Answers
The solution of the trigonometric equation is x = 30°
What is a trigonometric equation?A trigonometric equation is an equation that contains the trigonometric ratios sin, cos, tan, cosec, sec and cot.
How to solve the trigonometric equation?Given the trigonometric equation 3tanx - √3 = 0.
To solve the trigonometric equation, we proceed as follows.
Since we have
3tanx - √3 = 0.
Adding √3 to both sides of the equation, we have that
3tanx - √3 = 0
3tanx - √3 + √3 = 0 + √3
3tanx + 0 = √3
3tanx = √3
Next, we divide both sides of the equation by 3. So, we have that
3tanx = √3
3tanx/3 = √3/3
tanx = √3/3
To find x, we take the inverse tan of both sides. so, we have that
tanx = √3/3
tan⁻¹tanx = tan⁻¹(√3/3)
x = tan⁻¹(√3/3)
x = tan⁻¹(1.732/3)
x = tan⁻¹(0.5774)
x = 30°
So, the solution is x = 30°.
Learn more about trigonometric equation here:
https://brainly.com/question/28025415
#SPJ1
Calculate the particular solution for each of the folowing equations (CO2, PO1, C3x. \[ y^{\prime \prime}+4 y^{\prime}+3 y=0 \quad y(0)=2 \quad y^{\prime}(0)=1 \]
Answers
The particular solution for the given differential equation is y(x) = 2e^{-x} + e^{-3x}.
To find the particular solution, we first need to solve the homogeneous equation:
y'' + 4y' + 3y = 0
The characteristic equation associated with this homogeneous equation is:
r^2 + 4r + 3 = 0
Solving this quadratic equation, we find the roots:
(r + 3)(r + 1) = 0
r = -3 or r = -1
This gives us the homogeneous solution:
y_h(x) = C1e^{-3x} + C2e^{-x}
To find the particular solution, we use the initial conditions y(0) = 2 and y'(0) = 1. Let's substitute these values into the equation:
y(0) = 2e^{-0} + e^{-3(0)} = 2 + 1 = 3
y'(0) = -2C1 - C2 = 1
Now we solve these equations simultaneously:
-2C1 - C2 = 1 ---(1)
2 + C1 + C2 = 3 ---(2)
From equation (2), we have:
C1 + C2 = 1
Substituting this into equation (1), we get:
-2(1 - C2) - C2 = 1
-2 + 2C2 - C2 = 1
C2 = 3
Substituting C2 = 3 into equation (2), we find:
C1 + 3 = 1
C1 = -2
Therefore, the particular solution for the given differential equation is:
y(x) = -2e^{-3x} + 3e^{-x}
The particular solution for the given differential equation is y(x) = 2e^{-x} + e^{-3x}.
To know more about particular solution visit
https://brainly.com/question/31252913
#SPJ11
Solve for x in [0,2π) the following equation, 3cos(x)sin(x)=2sin(x). If necessary, round the solutions to the nearest hundredth of a radian. Question 14 Solve for x in [0,2π) the following equation, cos(2x)−2sin(x)−1=0. If necessary, round the solutions to the nearest hundredth of a radian.
Answers
The solutions, rounded to the nearest hundredth of a radian for the equation \(3cos(x)sin(x) = 2sin(x)\) in the interval [0, 2π) , are x = 0, x = 0.52, and x = 2.62.
The solutions, rounded to the nearest hundredth of a radian for the equation \(cos(2x) - 2sin(x) - 1 = 0\) in the interval [0, 2π) are x = 0.34, x = 1.16, x = 2.73, and x = 3.96.
To solve the equation, we can start by simplifying it. Notice that both sides of the equation have sin(x), so we can divide both sides by sin(x) without losing any solutions. This gives us 3cos(x) = 2.
Next, we can square both sides of the equation to eliminate the cosine term. This gives us \(9cos^2(x) = 4\). Rearranging the equation, we have \(cos^2(x) = 4/9\).
Taking the square root of both sides, we get cos(x) = ±\(\frac{2}{3}\). Now, we need to find the values of x where cos(x) equals \(\frac{2}{3}\).
Using the unit circle or a calculator, we find that cos(x) = \(\frac{2}{3}\) has solutions x = 0 and x = 2π. Similarly, cos(x) = -\(\frac{2}{3}\) has solutions x = 0.52 and x = 2.62.
However, we need to consider the original equation. For x = 0, the equation is satisfied. But for x = 2π, the equation becomes 3cos(2π)sin(2π) = 2sin(2π), which is equivalent to 0 = 0. Since this does not give us any new information, we can disregard x = 2π as a solution.
Therefore, the solutions to the equation 3cos(x)sin(x) = 2sin(x) in the interval [0, 2π) rounded to the nearest hundredth of a radian are x = 0 and x = 0.52, or approximately x = 0 and x = 2.62.
To solve the equation, we can start by rearranging it. Adding 1 to both sides, we have \(cos(2x) - 2sin(x) = 1.\)
Next, we can use the double-angle identity for cosine, which states that \(2cos^2(x) - 1 - 2sin(x) = 1\) = \(2cos^2(x) - 1\). Substituting this into the equation, we get \(2cos^2(x) - 1 - 2sin(x) = 1\).
Rearranging terms, we have \(cos(x) = ±\frac{2}{3}\). Dividing both sides by 2, we obtain \(cos(x) = ±\frac{2}{3}\) = 1.
Using the Pythagorean identity \(sin^2(x) + cos^2(x) = 1\), we can substitute \(sin^2(x)\) with \(1 - cos^2(x)\) in the equation. This gives us \(cos^2(x) - (1 - cos^2(x)) = 1.\)
Simplifying, we have \(2cos^2(x) - 1 = 1\). Rearranging terms, we get \(2cos^2(x) = 2\), which leads to \(cos^2(x) = 1\).
Taking the square root of both sides, we have cos(x) = ±1. Now, we need to find the values of x where cos(x) equals ±1 in the interval [0, 2π).
Using the unit circle or a calculator, we find that cos(x) = 1 has solutions x = 0 and x = 2π. Similarly, cos(x) = -1 has solutions x = 1.16 and x = 3.96.
Therefore, the solutions to the equation cos(2x) - 2sin(x) - 1 = 0 in the interval [0, 2π) rounded to the nearest hundredth of a radian are x = 0.34, x = 1.16, x = 2.73, and x = 3.96.
Learn more about interval here :
https://brainly.com/question/30882226
#SPJ11
Find the equation of a circle given the x intercepts as 3 and 9 and a point (5,-5)
Answers
The equation of the circle in standard form is: (x - 6)^2 + (y + 5)^2 = 9 Therefore, the center of the circle is (6, -5).
To find the equation of a circle, we need to determine the center and the radius of the circle. We can start by finding the x-coordinate of the center, which is the midpoint of the x-intercepts: (3 + 9)/2 = 6.
The y-coordinate of the center is the same as the y-coordinate of the given point, which is -5. Therefore, the center of the circle is (6, -5).
Next, we need to find the radius of the circle. We can use one of the x-intercepts and the center to do this. The distance between the x-intercept and the center is the radius, so we have: radius = |3 - 6| = 3
Therefore, the equation of the circle in standard form is: (x - 6)^2 + (y + 5)^2 = 9
Alternatively, we can expand the equation and rewrite it in general form: x^2 - 12x + 36 + y^2 + 10y + 25 = 9, x^2 + y^2 - 12x + 10y + 52 = 0, This is the equation of the circle in general form.
To know more about coordinates click here
brainly.com/question/29189189
#SPJ1
In the diagram shown at the right, ABCD is a parallelogram and BF = 16. Find the area of ABCD. Explain your reasoning. (Hint: Draw auxiliary lines through point A and through point D that are parallel to EH.)
Answers
The above question is a mathematical proof of the relationship between Lines and angles related to a Rhombus. See the proof below.
We know,
A Rhombus is a parallelogram with four sides (that is a quadrilateral). It's sides however are all of equal length.
we have,
∠DEC ≅ ∠BFC Reason = All Right Angles with Equal dimensions are congruent.
∠C ≅ ∠C Reason = It is the same angle for the two Right angles above which are congruent, hence Reflexive Property.
Δ DEC ≅ Δ BFC Reason = Angle Angle Side. The triangles are said to be congruent when two angles and a non-included side of one triangle match the corresponding angles and sides of another triangle.
≅ Reason = The corresponding parts of congruent triangles are congruent. Also, it is a parallelogram with all congruent sides.
ABCD is a Rhombus Reason = Its sides are all congruent.
Learn more about Rhombus at;
brainly.com/question/20627264
#SPJ1
complete question:
Given: ABCD is a parallelogram, FC is congruent to EC, DE bisects BC and BF bisects DC Prove: ABCD is a rhombus
Which angles are adjacent to each other

Answers
Answer:
7
Step-by-step explanation:
Answer:
4 and 1
Step-by-step explanation:
theyre beside each other
29) Explain the difference of the two expressions in the question.
What is the difference between (f g)(x) and (fog)(x)?
Answers
The function fg(x) seems to be the product of f and g, whereas the function fog(x) is the composition of f and g.
Definition of a composite function:A function whose values are discovered by applying another function to an independent variable and then applying that second function to the result, and whose domain consists of those possible values for which the result yielded by the first function lies inside the domain of both the second.
What kind of math are composite functions?A composite function is one that is dependent on another. When one function is swapped for another, a composite function is formed. For example, f(g(x)) is the composite function created when g(x) is replaced for x in f. (x). f(g(x)) can be translated as "f of g of x."
To know more about composite functions visit:
https://brainly.com/question/20379727
#SPJ9
I know I just asked a question but I really don’t understand it that much!
What percent of $72.40 = $18.10
Please help me,I will help you too if I can!
Answers
Answer:
25%
Step-by-step explanation:
18.1x4=72.4
Answer:
$18.10/ $72.40 * 100
=25%
Step-by-step explanation:
How do I do this right here

Answers
9/22 will be your answer
theres not much to explain this is the formula of probablity
Always remember to use (Number of favorable outcomes) ÷ (Sample space).
wish you the best!
1. Two similar triangles are
pictured below. What is the
length of side z based on the
information given?

Answers
Answer:
5
Step-by-step explanation:
4 x 6= 24 x 1/2 = 12
10-6 = 4 x 4 = 16
cut a imaginary line above line (4) . that sapce below it is 4x4.
1 is the remaining distance for the top.
4+1=5
what do you do on this i need it asap 40 + 56 ÷ p - q
Answers
Answer:
40 + 56/p - q
Step-by-step explanation:
This equation is weird. Your answer should be 40 + 56/p - q
The only thing that would change is writing "56 ÷ p" as a fraction.
Now, here's the weird part.
If you try to solve it after rewriting "56 ÷ p" as a fraction, your answer would look like this:
40p + 56 − qp
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
p
Unless you have a math-based keyboard that would write 40p + 56 − qp over p as a fraction formatted like the equation shown above (instead of having to put a bunch of dashes so it looks like a long fraction line), then I'd stick with just typing 40 + 56/p - q.
let f be a function that is continuous on the closed interval 2 4 with f(2)=10 and f(4)=20
Answers
There exists a value c in the interval (2, 4) such that f(c) = 15.
Given that f is a function that is continuous on the closed interval [2, 4] and f(2) = 10 and f(4) = 20, we can use the Intermediate Value Theorem to show that there exists a value c in the interval (2, 4) such that f(c) = 15.
The Intermediate Value Theorem states that if a function f is continuous on a closed interval [a, b], and if M is any value between f(a) and f(b) (inclusive), then there exists at least one value c in the interval (a, b) such that f(c) = M.
In this case, f(2) = 10 and f(4) = 20, and we are interested in finding a value c such that f(c) = 15, which is between f(2) and f(4). Since f is continuous on the interval [2, 4], the Intermediate Value Theorem guarantees that such a value c exists.
Therefore, there exists a value c in the interval (2, 4) such that f(c) = 15.
Learn more about continuos function at https://brainly.com/question/22981061
#SPJ11
let p be the price of an item. the unit sales of the item are 200 - 5p. what is the correct formula for the revenue generated by the item?
Answers
The correct formula for the revenue generated by the item is Revenue = 200p - 5p^2.
The revenue generated by the item can be calculated by multiplying the price (p) by the unit sales (200 - 5p). Therefore, the correct formula for the revenue generated by the item is:
Revenue = Price x Unit Sales
Revenue = p(200 - 5p)
Revenue = 200p - 5p^2
The revenue generated by the item is a quadratic function of the price (p). To find the maximum revenue, we need to differentiate the function with respect to p and set it equal to zero:
dRevenue/dp = 200 - 10p = 0
10p = 200
p = 20
Therefore, the maximum revenue is generated when the price of the item is $20. Substituting p = 20 in the revenue formula, we get:
Revenue = 200(20) - 5(20^2) = $2000
Hence, the correct formula for the revenue generated by the item is Revenue = 200p - 5p^2, and the maximum revenue is achieved when the price of the item is $20, generating a revenue of $2000.
Know more about revenue here,
https://brainly.com/question/29567732
#SPJ11
In a statistical display, each data value should be represented by the same amount of area. this is known as the?
Answers
Area Principle. In a statistical display, each data value should be represented by the same amount of area. Bar chart (Relative Frequency Bar Chart)
Using rectangular bars with heights or lengths proportional to the values they represent, a bar chart or bar graph displays categorical data. Both a vertical and a horizontal bar plot are possible. A column chart is another name for a vertical bar graph.
Using rectangular bars with heights or lengths proportional to the values they represent, a bar chart or bar graph displays categorical data. Both a vertical and a horizontal bar plot are possible. A column chart is another name for a vertical bar graph.
Learn more about bar chart here
https://brainly.com/question/24741444
#SPJ4
Which values of x and y make RAPT a parallelogram?
Answers
The values of x and y that make RAPT a parallelogram are;
x = 15 and y = 25
How to find the angles of a Parallelogram?Angle T and angle P are supplementary angles by parallel lines. Thus they sum up to 180 degrees and we have;
3x + 10 + 8x + 5 = 180
11x + 15 = 180
11x = 165
x = 15
T = 55°
P = 125°
Likewise R and T are supplementary angles by parallel lines and so we have;
55 + 5y = 180
5y = 180 -55
5y = 125
y = 25
R = 125°
A must be 55° since the angles add up to 360°.
R + A + P + T =
125 + 55 + 125 + 55 = 360°
Read more about angles of a Parallelogram at; https://brainly.com/question/24056495
#SPJ1

Multiply: (6x - 1)(6x +1)
Answers
Answer:
36x^2 -1
Step-by-step explanation:
6x times 6x= 36x^2
6x times 1= 6x
-1 times 6x= -6x
-1 times 1= -1
so, ...
36x^2+6x+(-6x)+(-1) = 36x^2 -1
Solve for x.
a. 16
b. 11
c. 6
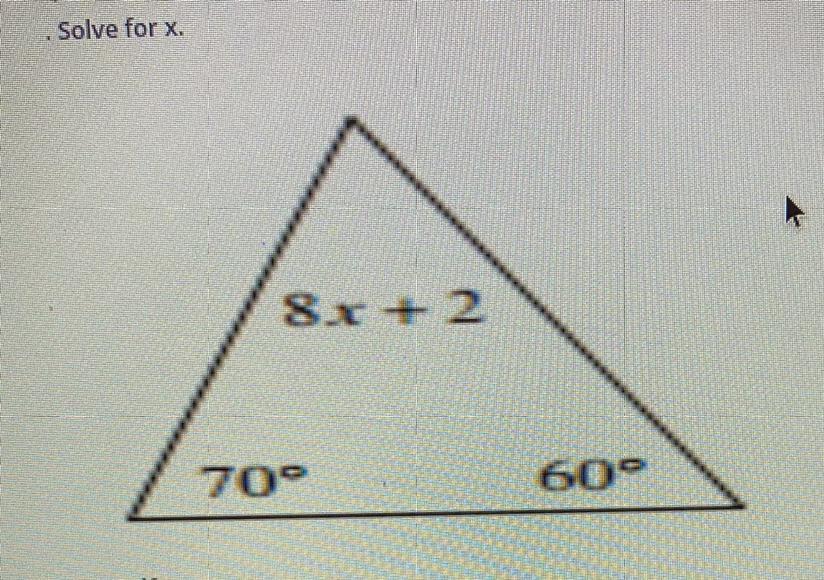
Answers
a triangles angles must add up to 180 degrees. 70+60=130 so 180-130=50. so the last angle is 50 degrees. then u set up 8x+2=50 and solve.
If S= (4, -6) and T= (5, -1), find the sum of S + T
Answers
Sum of coordinates, S + T = (9 , -7)
What is coordinate?A coordinate is an address, which helps to locate a point in space. For a two-dimensional space, the coordinates of a point are (x, y). Here let us take note of these two important terms.
Abscissa: It is the x value in the point (x, y), and is the distance of this point along the x-axis, from the origin
Ordinate: It is the y value in the point (x, y)., and is the perpendicular distance of the point from the x-axis, which is parallel to the y-axis.
Given,
S = (4 , -6)
T = (5 , -1)
S + T = (4 , -6) + (5 , -1)
= (4 + 5 , -6 + -1)
= (9 , -7)
Hence, S + T = (9 , -7) is sum of coordinates of point S and T
Learn more about coordinates here:
https://brainly.com/question/18402024
#SPJ1
Help! Do you guys have any studying tips & how to get good grades?
Answers
I'm not exactly at the best place atm (especially because i was using this app all day lol) but if suggest doing the smaller, easier things first. Then moving to things you are more intrested in and excel at. If you ahve something that is a priority, try and move that after the first couple easy things or immediate.
Answer:
honestly just take good notes and pay attention in class. when studying make sure you are in a quiet area and make sure you know what youre studying. when it comes to getting good grades pay attention in class. do not be afraid to ask your teacher questions. good luck :)
tell how the transformed function, g(x), compares to the parent function, f(x). f(x)=5^x+2;g(x)=5^-x+6
Answers
Compared to the parent function f(x), the transformed function g(x) is shifted 4 units upwards and has a reflection across the y-axis. This means that the graph of g(x) is a mirror image of the graph of f(x) with respect to the y-axis and is shifted upwards by 4 units.
The transformation of g(x) reflects the original function f(x) across the y-axis and moves it up by 4 units. This change results in a different shape for the graph of g(x) compared to f(x).
What is the difference between an outcome and an event?
Answers
Answer: Is this for math?
The result of a random experiment will be called an outcome, and combination of outcomes will be termed as event, i.e. An Event is a one or more outcome of an experiment.
For example: Whenever we do an experiment like rolling a die, we get an outcome, i.e. if we roll a die we get an outcome of 1, 2, 3, 4, 5, or 6.
An event is a set of outcomes. The event of rolling an even number with a die is the set.
{2, 4, 6}.
Also, We call the set of all possible outcomes of an experiment the sample space, and the sample space for the experiment of rolling a die is
Step-by-step explanation:
An outcome and an event are related but distinct concepts. explain below.
Outcome:
An outcome refers to a single possible result of an experiment or a random process.
In other words, it represents the individual elements of the sample space.
For example, when flipping a fair coin, the possible outcomes are heads and tails.
In rolling a standard six-sided die, the outcomes are the numbers 1, 2, 3, 4, 5, and 6.
Each outcome represents a specific and unique result that could occur in the given situation.
Event:
An event, on the other hand, is a collection or set of outcomes. It represents a specific combination of outcomes that have some significance or interest in the context of the experiment. Events can include one or more outcomes.
For example, in rolling a die, the event rolling an even number includes the outcomes 2, 4, and 6.
Another event could be rolling a number greater than 4, which includes the outcomes 5 and 6.
Events can be simple or compound.
Conclusion: an outcome is a single result of an experiment, while an event is a combination of one or more outcomes with some specific meaning or interest for the given situation.
Learn more about Outcomes here:
https://brainly.com/question/2495224
#SPJ6
Two angles form a linear pair. The measure of one angle is x and the measure of the other angle is 1.4 times x plus 12∘ . Find the measure of each angle.
Answers
Answer:
70° and 110°
Step-by-step explanation:
If two angles forms a linear pair, this means that the sum of the angles is 180°. If the measure of one angle is x and the measure of the other angle is 1.4 times x plus 12∘
Let A be the first angle = x°
Let B be the second angle = (1.4x+12)°
Since they form a linear pair, then
A+B = 180°
x + 1.4x+12 = 180°
2.4x = 180-12
2.4x = 168
x = 168/2.4
x = 70°
The measure of angle A = 70°
The measure if angle B = 1.4x+12
B = 1.4(70)+12
B = 98+12
B = 110°
The measure of both angles are 70° and 110°
5. Bryce gets a monthly allowance of $10 plus $1 for each
additional chore.
A) Determine if the situation is linear or not.
B) Determine if the situation is proportional or not.
C) Determine if the situation is a function or not.
How can you tell? Be sure to use the words input, output, slope and y-intercept in your
explanation.

Answers
report errorin the top row of an $8 \times 8$ chessboard, hamza writes the values $1, 2, 4, 8, 16, 32, 64, 128$. in the leftmost column, hamza writes the values $1, 3, 9, 27, 81, 243, 729, 2187$. in each of the remaining empty squares, hamza writes the product of the leftmost number in that square's row and the topmost number in that square's column.what is the sum of all the numbers on the chessboard?
Answers
The sum of all the numbers on the chessboard is 4036, obtained by summing the values in the top row, leftmost column, and the products in the remaining squares.
The sum of all the numbers on the chessboard can be found by summing the values in the top row, the values in the leftmost column, and the products in the remaining squares.
The sum of the values in the top row is 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 = 255.
The sum of the values in the leftmost column is 1 + 3 + 9 + 27 + 81 + 243 + 729 + 2187 = 3270.
The sum of the products in the remaining squares can be calculated by finding the sum of the geometric series 1 + 2 + 4 + ..... + 128. Using the formula for the sum of a geometric series, this sum is 2⁸⁺¹ - 1 = 2⁹ - 1 = 511.
Therefore, the sum of all the numbers on the chessboard is 255 + 3270 + 511 = 4036.
To know more about geometric series:
https://brainly.com/question/30264021
#SPJ4
Find the missing value.
(√24-√k)(√24+√k)=5
Answers
Answer:
K=19
Step-by-step explanation:
MY WRITTEN RESPONCE BELOW
