A cabin was built in the shape of a rectangle. It is 15 meters (m) long and 10 m wide. How far is it all the way around the outside of the cabin?
Which of these shows a way to solve the problem?
Answers
The way around the outside of the cabin is 50 meters
How far is it all the way around the outside of the cabin?The given parameters are:
Length = 15 meters
Width = 10 meters
The way around the outside of the cabin is the perimeter and it is calculated as
Perimeter = 2 * (Length + Width)
So, we have
Perimeter = 2 * (15 + 10)
Evaluate
Perimeter = 50 meters
Hence, the way around the outside of the cabin is 50 meters
Read more about perimeter at
https://brainly.com/question/24571594
#SPJ1
Related Questions
Find the equation of the line perpendicular to y=1/2x-1 and passes through the point (5,6)
Answers
The equation of the line perpendicular to y=1/2x-1 and passing through the point (5,6) is y = -2x + 16.
To find the equation of the line perpendicular to y=1/2x-1, we need to determine its slope. We can recall that the slope of a line in slope-intercept form, y = mx + b, is given by m, the coefficient of x. So in the given equation y=1/2x-1, the slope is 1/2.
The slope of a line perpendicular to this line will be the negative reciprocal of the slope, which means it will be -2. To see why this is true, remember that the product of the slopes of two perpendicular lines is always -1. So if the slope of the original line is m, the slope of the perpendicular line will be -1/m.
Now that we know the slope of the perpendicular line is -2, we can use the point-slope form of the equation of a line to find its equation. The point-slope form is:
y - y1 = m(x - x1)
where m is the slope and (x1, y1) is a point on the line.
We are given a point on the perpendicular line, (5, 6), so we can substitute that into the equation and also substitute in the slope, -2:
y - 6 = -2(x - 5)
y - 6 = -2x + 10
y = -2x + 16
Hence, the equation of the line perpendicular to y=1/2x-1 and passing through the point (5,6) is y = -2x + 16.
To learn more about Line of Perpendicular and Slope of a line, refer to the following answers:
https://brainly.com/question/25842670
https://brainly.com/question/30422569
Is height always a statistical subject
Answers
Answer:
It Is!
Step-by-step explanation:
"For example, “How old am I?” is not a statistical question, but “How old are the students in my school?” is a statistical question because one anticipates variability in students' ages."
(i) Write the zeroes of the polynomial by using above graph.
(ii)Form a quadratic polynomial for above graph.
(iii)If a,1/a are the zeroes of polynomial 2x² -x +8k, then find the value of k.
please answer
no spam only for darkparadox #darkparadox

Answers
There is no real Value of k that will satisfy the equation 2x² - x + 8k = 0 if a and 1/a are the roots of the polynomial.
(i) Zeroes of the polynomial:
In the graph, we have two points where the curve intersects the x-axis: one is at (-1,0), and the other is at (2,0).The corresponding values of x are -1 and 2, and they are the zeros of the polynomial. Therefore, the zeros of the polynomial are -1 and 2.(ii) Forming the quadratic polynomial:
From the graph, we can observe that the curve intersects the y-axis at the point (0,5), implying that the constant term of the polynomial is 5.
We can use the formula to find the quadratic polynomial if we have two zeros and one constant term. Thus, the quadratic polynomial is given by:(x + 1)(x - 2) = x² - x - 2x + 2 = x² - 3x + 2. Therefore, the quadratic polynomial is x² - 3x + 2.(iii) Value of k if a, 1/a are the zeroes of the polynomial 2x² - x + 8k:
We know that a and 1/a are the zeroes of the polynomial 2x² - x + 8k. Therefore, we can find the sum and product of the roots and use them to determine the value of k.
The sum of the roots is a + 1/a, and their product is a(1/a) = 1. Using the sum and product of the roots, we can write: a + 1/a = 1/2 (1/2 is the coefficient of x)Substituting a with 1/a in the above equation, we get: 1/a + a = 1/2Multiplying both sides of the equation by 2a, we get: 2 + 2a² = a
Simplifying the equation, we get: 2a² - a + 2 = 0Multiplying both sides by 2,
we get: 4a² - 2a + 4 = 0Dividing both sides by 2, we get: 2a² - a + 2 = 0
Using the quadratic formula, we get: a = [1 ± √(1 - 4(2)(2))]/(2(2))
Simplifying, we get: a = [1 ± √(-31)]/4Since the discriminant of the quadratic formula is negative, the roots are imaginary. Therefore, there is no real value of k that will satisfy the equation 2x² - x + 8k = 0 if a and 1/a are the roots of the polynomial.
For more questions on Value .
https://brainly.com/question/843074
#SPJ8
if m<1=2x+2 and m<2=9x, find m<1
Answers
Answer:
18/7
Step-by-step explanation:
Since m<2 includes 1, m<2 = m<1
9x = 2x + 2 ⇒ 7x = 2 ⇒ x = 2/7
m<1 = 2(2/7) + 2 = 4/7 + 14/7 = 18/7
algebra domain and range please help

Answers
Answer:
Option 2.
Step-by-step explanation:
Find the domain by finding where the function is defined. The range is the set of values that correspond with the domain.
Domain: \((- \infty} ,0)\) ∪ \((0, \infty} )\)
Range: \((- \infty} ,0)\)∪\((0, \infty} )\)
Find the surface area

Answers
Check the picture below.
so hmmm let's find the length of the slanted side, namely the hypotenuse of the triangle with sides of 9 and 7(half of 14).
\(\begin{array}{llll} \textit{using the pythagorean theorem} \\\\ c^2=a^2+o^2\implies c=\sqrt{a^2 + o^2} \end{array} \qquad \begin{cases} c=hypotenuse\\ a=\stackrel{adjacent}{9}\\ o=\stackrel{opposite}{7} \end{cases} \\\\\\ c=\sqrt{ 9^2 + 7^2}\implies c=\sqrt{ 81 + 49 } \implies c=\sqrt{ 130 }\)
so now let's get the areas of those triangles and those rectangles.
\(\stackrel{\textit{two triangles}}{2\left[\cfrac{1}{2}(14)(9) \right]}~~ + ~~\stackrel{\textit{left and right rectangles}}{2(\sqrt{130})(20)}~~ + ~~\stackrel{\textit{bottom rectangle}}{(20)(14)} \\\\\\ 126+40\sqrt{130}+280\implies 406+40\sqrt{130} ~~ \approx ~~ \text{\LARGE 862.07}~cm^2\)

With the spinner shown, the theoretical probability of landing on 2 is 0.25. Which number of spins would most likely result in a relative frequency that is closest to the theoretical probability?
Answers
just give the other kid brainiest
Step-by-step explanation:
# 5 pls !!
find dy/dx by implicit differentiation

Answers
Step-by-step explanation:
\(5. {x}^{3} - xy + {y}^{2} = 4\)
\( \frac{dy}{dx} ( {x}^{3} - xy + {y}^{2} ) = \frac{dy}{dx} (4)\)
\(3 {x}^{2} - x(1) \frac{dy}{dx} + 1(y) + 2y \frac{dy}{dx} \)
Combine the dy/dx.
\( \frac{dy}{dx} ( - x + 2y) + y + 3 {x}^{2} \)
\( \frac{dy}{dx} ( - x + 2y) = - 3 {x}^{2} - y\)
\( \frac{dy}{dx} = \frac{ - 3 {x}^{2} - y}{ - x + 2y} \)
\( \frac{3 {x}^{2} + y }{x - 2y} \)
Answer:
\(\frac{dy}{dx}\) = \(\frac{y-3x^2}{2y-x}\)
Step-by-step explanation:
using the product rule to differentiate - xy then
3x² - (x\(\frac{dy}{dx}\) + y(1) ) + 2y\(\frac{dy}{dx}\) = 0
3x² - x\(\frac{dy}{dx}\) - y + 2y\(\frac{dy}{dx}\) = 0
3x² + \(\frac{dy}{dx}\) (2y - x) - y = 0 (subtract 3x² - y from both sides )
\(\frac{dy}{dx}\) (2y - x) = y - 3x² ← divide both sides by (2y - x)
\(\frac{dy}{dx}\) = \(\frac{y-3x^2}{2y-x}\)
Root of the equation
Answers
Answer:
A fancy way of saying "solutions" of the equation
what is the value of this expression?

Answers
Answer:
20
Step-by-step explanation:
4 + \((m-n)^{4}\) ← substitute m = 7 and n = 5 into the expression
= 4 + \(7-5)^{4}\)
= 4 + \(2^{4}\)
= 4 + 16
= 20
Ken built a square fence around his yard. He planted 4 trees on each side of the fence. What is the least number of trees Ken planted?
A. 4
B. 12
C. 19
D. 20
Answers
Answer:
12
Step-by-step explanation:
edge 1045
The angle formed between one side and another, always less than 180 degrees.
Answers
Answer:obtuse angle
Step-by-step explanation:
An obtuse angle is an angle of greater than 90° and less than 180°. It is bigger than an acute angle. It is smaller than a straight angle, which measures 180°. Angles are measured with a protractor obtuse angle is specifically present in hexagon and pentagon and others.
12a-12b+12c please help to simplify
Answers
Answer:
12(a+b+c)
Step-by-step explanation:
how to verify:
Distribute 12 and you'll get the original expression
I hope my answer was helpful!
What is the domain of this function?
-1>2 3>6 5>8
A (2, 6, 8)
B. (2, 6, 8,3, 5)
C. (-1,3, 5)
D. (3)

Answers
It's Letter C. 1 3 and 5
that's the domain
(a) The number of terms in an arithmetic progression is 40 and the last is -54. Given that the sum of the 15 terms added to the sum of the first 30 terms is zero. Calculate (1) The first term and common difference, (ii) the sum of the progression.
Answers
(i) The first term (a) is 24 and the common difference (d) is -2.
(ii) The sum of the progression is 2520.
i) Finding the first term and common difference:
Given that the number of terms in the arithmetic progression is 40 and the last term is -54, we can use the formula for the nth term of an arithmetic progression to find the first term (a) and the common difference (d).
The nth term formula is: An = a + (n-1)d
Using the given information, we can substitute the values:
-54 = a + (40-1)d
-54 = a + 39d
We also know that the sum of the first 15 terms added to the sum of the first 30 terms is zero:
S15 + S30 = 0
The sum of the first n terms of an arithmetic progression can be calculated using the formula:
Sn = (n/2)(2a + (n-1)d)
Substituting the values for S15 and S30:
[(15/2)(2a + (15-1)d)] + [(30/2)(2a + (30-1)d)] = 0
Simplifying the equation:
15(2a + 14d) + 30(2a + 29d) = 0
30a + 210d + 60a + 870d = 0
90a + 1080d = 0
a + 12d = 0
a = -12d
Substituting this value into the equation -54 = a + 39d:
-54 = -12d + 39d
-54 = 27d
d = -2
Now we can find the value of a by substituting d = -2 into the equation a = -12d:
a = -12(-2)
a = 24
Therefore, the first term (a) is 24 and the common difference (d) is -2.
ii) Finding the sum of the progression:
The sum of the first n terms of an arithmetic progression can be calculated using the formula:
Sn = (n/2)(2a + (n-1)d)
Substituting the values:
S40 = (40/2)(2(24) + (40-1)(-2))
S40 = 20(48 - 39(-2))
S40 = 20(48 + 78)
S40 = 20(126)
S40 = 2520
Therefore, the sum of the arithmetic progression is 2520.
for such more question on common difference
https://brainly.com/question/25731911
#SPJ8
What is 63 ÷ 9 + 5y3 when y = 2?
37
47
72
96
Answers
37
Hope it helps
Good luck
Answer:
(63 ÷ 9) + 5 x 2 x 3 we use BODMAS
7 + 10 X 3
7 + 30=37
Step-by-step explanation:
Professor A.B.C company opens his own company, Electronic Tutorial Services, and completes the following transactions in June:
6/1 A.B.C company invests 20,000 in the business.
6/3 Purchased 12,100 of equipment.
6/4 Paid 220 premium for an insurance policy.
6/6 Purchased office supplies on Account 140.
6/9 Purchased a new computer for 9,000. Paid 40% cash agreed to pay the remainder Later.
6/10 Billed student Omar 58 for tutorial services that were performed.
6/14 Paid for the supplies purchased on June 6th.
6/15 the owner suggested to purchased new Building for his company by 22,000
6/25 Received 85 cash from student Salim Ali for tutorial services performed.
6/30 Student billed on June 10 pays the amount due to A.B.C company.
6/30 A.B.C company withdraws 60 for personal use.
Required: Prepare the all Accounting Cycles
Answers
In June, A.B.C company invested $20,000, purchased equipment, paid insurance premium, bought office supplies, billed students for tutorial services, received cash, paid for supplies, withdrew personal funds.
Accounting Cycles:
1. June 1:
- A.B.C company invests $20,000 in the business.
- Prepare the journal entry:
- Debit: Cash ($20,000)
- Credit: Capital ($20,000)
2. June 3:
- Purchased equipment for $12,100.
- Prepare the journal entry:
- Debit: Equipment ($12,100)
- Credit: Cash ($12,100)
3. June 4:
- Paid $220 premium for an insurance policy.
- Prepare the journal entry:
- Debit: Insurance Expense ($220)
- Credit: Cash ($220)
4. June 6:
- Purchased office supplies on account for $140.
- Prepare the journal entry:
- Debit: Office Supplies ($140)
- Credit: Accounts Payable ($140)
5. June 9:
- Purchased a new computer for $9,000. Paid 40% in cash and agreed to pay the remainder later.
- Prepare the journal entry for the cash payment:
- Debit: Computer ($3,600) [40% of $9,000]
- Credit: Cash ($3,600)
- Prepare the journal entry for the remaining amount:
- Debit: Computer ($5,400)
- Credit: Accounts Payable ($5,400)
6. June 10:
- Billed student Omar $58 for tutorial services performed.
- Prepare the journal entry:
- Debit: Accounts Receivable ($58)
- Credit: Tutorial Services Revenue ($58)
7. June 14:
- Paid for the supplies purchased on June 6th ($140).
- Prepare the journal entry:
- Debit: Accounts Payable ($140)
- Credit: Cash ($140)
8. June 15:
- The owner suggested purchasing a new building for the company for $22,000.
- No journal entry is required at this point. It is a decision made by the owner.
9. June 25:
- Received $85 cash from student Salim Ali for tutorial services performed.
- Prepare the journal entry:
- Debit: Cash ($85)
- Credit: Accounts Receivable ($85)
10. June 30:
- Student billed on June 10 pays the amount due ($58).
- Prepare the journal entry:
- Debit: Cash ($58)
- Credit: Accounts Receivable ($58)
11. June 30:
- A.B.C company withdraws $60 for personal use.
- Prepare the journal entry:
- Debit: Withdrawals ($60)
- Credit: Cash ($60)
These transactions represent the accounting cycles for the given period.
For more such questions on cash, click on:
https://brainly.com/question/14883253
#SPJ8
What is the formula for slope?
Will give brainliest for first correct.
Answers
Answer:
To solve the problems in this lesson, students use the slope formula, which states that m = (y2 -- y1) / (x2 -- x1). The slope formula can be read as "slope equals the second y coordinate minus the first y-coordinate over the second x-coordinate minus the first x-coordinate".
Hope helps

Have a great day!
factorise:x^3-(y-z)^3
Answers
The factorized form of \(x^3 - (y - z)^3\ is \ (x - y + z)(x^2 - xy + 2xz + yz - 2z^2).\)
The Factorization is derived from the application of a mathematical identity. As an AI language model, the information provided is generated based on existing knowledge and formulas.
The given expression is \(x^3 - (y - z)^3.\)To factorize it, the difference of cubes, which states that a^3 - b^3 can be factorized as\((a - b)(a^2 + ab + b^2).\)
Applying this identity to our expression, we have:
\(x^3 - (y - z)^3 = (x - (y - z))((x - (y - z))^2 + (x - (y - z))(y - z) + (y - z)^2)\)
Simplifying further, we get:
\(= (x - y + z)(x^2 - 2xy + 2xz - y^2 + 2yz - z^2 + xy - y^2 + yz - z^2 + y^2 - 2yz + z^2)\\= (x - y + z)(x^2 - 2xy + xy + 2xz + yz - 2yz - y^2 + y^2 - y^2 + 2yz - 2z^2 + y^2 - z^2 + z^2)\\= (x - y + z)(x^2 - xy + 2xz + yz - 2z^2)\)
So, the factorized form of \(x^3 - (y - z)^3 \ is\ (x - y + z)(x^2 - xy + 2xz + yz - 2z^2).\)
the above factorization is derived from the application of a mathematical identity.
To know more about factorized .
https://brainly.com/question/14268870
#SPJ11
27,813 students took the ACET this year. If only 2,836 students were admitted into the Ateneo among those students, what is the Ateneo’s acceptance rate? a. 7.5% b. 10.2% c. 13.4% d. 9.0%
Answers
If only 2,836 students were admitted into the Ateneo among 27,813 students, who took the ACET this year, the Ateneo’s acceptance rate is b. 10.2%.
How the rate is determined:The rate is the ratio of one value, expression, measurement, or quantity compared to another.
The rate represents the quotient of the numerator and the denominator.
The rate is expressed as a percentage by multiplication with 100.
The number of students who took the ACET this year = 27,813
The number of students who were admitted into the Ateneo = 2,836
The percentage or rate admitted = 10.19667% (2,836 ÷ 27,813 × 100)
= 10.2%
Thus, we can conclude that the acceptance rate or percentage is Option B.
Learn more about determining the percentage at https://brainly.com/question/24877689.
#SPJ1
The graph shows the equation y = 2x – 3. Use the slider for a to move the vertical line on the graph. Based on the vertical line test, is this equation a function? Why or why not?
Answers
Answer:
Yes. The vertical line never touches the graph at more than one point at the same time.
Step-by-step explanation:
this is the plato and edmentum answer
(make sure this is the right question)
As the vertical line touches the graph of the equation y = 2x - 3 it is a function.
What is a graph?The set of ordered pairings (x, y) where f(x) = y makes up the graph of a function.
These pairs are Cartesian coordinates of points in two-dimensional space and so constitute a subset of this plane in the general case when f(x) are real values.
Given, An equation y = 2x - 3.
Now, If we draw a vertical line and it touches the graph at only one point
the equation is a function but if the vertical line touches the graph at more than two points the equation is not a function.
learn more about graphs here :
https://brainly.com/question/2288321
#SPJ2

The function G(m) = 49.5m + 89.75 represents the cost of joining the gym in addition to the one time membership fee. The cost, G, is measured in dollars for m months. 1. Find the value of G(6).
Answers
Answer:
386.75
Step-by-step explanation:
added in the picture
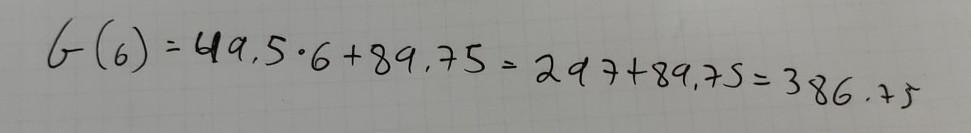
The cost of joining the gym for 6 months is 386.75.
Given,
The function G(m) = 49.5m + 89.75 represents the cost of joining the gym in addition to the one-time membership fee.
The cost, G, is measured in dollars for m months.
We need to find the value of G(6).
Here,
The one-time membership = 89.75.
Now,
Putting m = 6 months in:
G(m) = 49.5m + 89.75
G(6) = 49.5 x 6 + 89.75
= 297 + 89.75
= 386.75
Thus the cost of joining the gym for 6 months is G(6) = 386.75.
Learn more about finding the value of a function here:
https://brainly.com/question/8822000
#SPJ2
choose the correct response
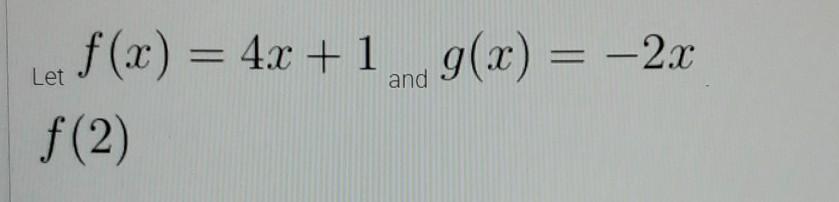
Answers
Answer:
f(2) = 9
Step-by-step explanation:
It's give in the question,
Two different functions are,
f(x) = 4x + 1
g(x) = -2x
Then we have to find the output value of function 'f' for the input value x = 2.
By substituting the value of x in the function 'f',
f(2) = 4(2) + 1
= 9
f(2) = 9
The weight of a product is normally distributed with a mean of 4 ounces and a variance of .25 squared ounces. What is the probability that a randomly selected unit from a recently manufactured batch weighs more than 5 ounces
Answers
Answer: 0.0228
Step-by-step explanation:
Let x be the weight of a product.
The probability that a randomly selected unit from a recently manufactured batch weighs more than 5 ounces:
\(P(X>5)\\\\=P(\dfrac{X-Mean}{\sqrt{Variance}}>\dfrac{5-4}{\sqrt{0.25}})\\\\=P(Z>\dfrac{1}{0.5}) \ \ \ [z=\dfrac{X-Mean}{\sqrt{Variance}}]\\\\=P(z>2)\\\\=1-P(Z<2)\\\\=1-0.9772\ \ [\text{Using p value table}]\\\\=0.0228\)
Hence, the required probability = 0.0228
Find the y intercept if there is one enter answer as a ordered pair

Answers
Based on the graph, we can see that the line passes through the point (0,3) as the line is horizontal, therefore the y-intercept is (0,3).
Answer:
(0,4)
Step-by-step explanation:
its where it intersects with the y axis
What is the range of function represented by this graph?

Answers
f(x)=-(x+4)(x+2)
So the range is (-oo,1]
Consider oo as infinity sign
A grocery store sells four different jars of peanut butter. Determine which is the best buy, based on the cost per unit. 16 ounces for $1.70 20 ounces for $1.90
26 ounces for $3.33 40 ounces for $4.64
Answers
Answer this question please

Answers
Answer:
Step-by-step explanation:
we know this is a 2 dimensional shape so m*3 out, its m not ft so only answer is
24 m*2
Each volleyball set costs $63.74.
Which equation represents the cost, c, of n sets?
Answers
The equation that represents the cost, c, of n sets is c = 63.74n
Which equation represents the cost, c, of n sets?from the question, we have the following parameters that can be used in our computation:
Each volleyball set costs $63.74.
Let the total number of sets be n
So we have
Cost of n = 63.74 * n
This gives
c = 63.74n
Hence, the equation is c = 63.74n
Read more about equation at
https://brainly.com/question/32492977
#SPJ1
Kevin and Randy Muise have a jar containing 80 coins, all of which are either quarters or nickels. The total value of the coins in the jar is $11.80. How many of each type of coin do they have?
Answers
Answer:
39 quarters and 41 nickelsStep-by-step explanation:
Let the number of quarters be x and nickels be y.
Given:
Quarter is 25 centsNickel is 5 centsNumber of coins is 80Total amount is $11.80 = 1180 centsWe have equations:
x + y = 8025x + 5y = 1180Solve the system by elimination, subtract 5 times the first equation from the second one:
25x + 5y - 5x - 5y = 1180 - 80*520x = 780x = 780/20x = 39Find the value of y:
39 + y = 80y = 80 - 39y = 41Verify:
25*39 + 5*41 = 975 + 205 = 1180