Big Points for this one. This is my big cousins account, I’m in 5th grade and I need help
You received 1⁄4 pound of candy from your grandmother, 1⁄2 pound of candy from your sister, and 1⁄8 pound of candy from your best friend. How many pounds of candy did you receive?
pound
Answers
Answer:
7/8
Step-by-step explanation:
Use this format for the problem:
Total pounds of candy you received = Pounds of candy received from Grandmother + Pounds of candy received from Sister + Pounds of Candy received from Best Friend
Add them all up to find the total you received.Total pounds of candy you received = 1/4 + 1/2 + 1/81. Simplify the expression
\(\frac{1}{4}+ \frac{1}{2}+ \frac{1}{8}\)
Find the lowest common denominator:
\(\frac{\left(1\cdot 2\right)}{\left(4\cdot 2\right)}+\frac{\left(1\cdot 4\right)}{\left(2\cdot 4\right)}+\frac{1}{8}\)
Multiply the denominators:
\(\frac{\left(1\cdot 2\right)}{8}+\frac{\left(1\cdot 4\right)}{8}+\frac{1}{8}\)
Multiply the numerators:
\(\frac{2}{8}+\frac{4}{8}+\frac{1}{8}\)
Combine the fractions:
\(\frac{\left(2+4+1\right)}{8}\)
Combine the numerators:
\(\frac{7}{8}\)
Hence, the answer is 7/8.
___________
Why learn this
- Let's say you invite ten friends over for movie night and order four pizzas to split. How do you divide the pizza evenly so everyone gets the same amount of pizza? If each section of the couch can fit 1+1/5 people, how many sections would there need to be to accommodate all of your friends? The whole world is made up of little bits and pieces that are part of something larger, and the key to understanding them is fractions.
Fractions are the mathematical representation of any whole thing that is made up of multiple parts. Knowing how to manipulate them using operations like addition, subtraction, multiplication, and division is one of the most widely applicable math skills in everyday situations and provides an important foundation for other math concepts you will encounter.
Terms and topics
Operations with fractions__________________
Level: 5th grade
Unit: Operations with fractions
Step-by-Step Explanation:
From Grandmother = 1/4 pound
From Sister = 1/2 pound
From Best Friend = 1/8 pound
Therefore,
= 1/4 + 1/2 + 1/8
= 2/8 + 4/8 + 1/8
= 6/8 + 1/8
=> 7/8
Total Pounds of Candy = 7/8 pound
Related Questions
what is 2/5 x 4 help me please
Answers
Answer: 1.6
Step-by-step explanation:
Answer:
1.6
Step-by-step explanation:
2/5×4
=8/5
=1.6
So the answer is 1.6
It took Aiden 6 hours to plant 8 trees. How many hours would it take for him to plant 20 trees? 24, 18, 23, 15
Answers
================================================
Work Shown:
(6 hours)/(8 trees) = (x hours)/(20 trees)
6/8 = x/20
6*20 = 8*x ... cross multiply
120 = 8x
8x = 120
x = 120/8
x = 15
It takes him 15 hours to plant 20 trees.
Write down two factors of 24 that are primenumber
Answers
the prime factors of 24 are 2 and 3, which combine to give the unique prime factorization of 24 as 2^3 × 3.
There are no factors of 24 that are prime numbers. A factor of a number is a whole number that divides that number without leaving a remainder. Prime numbers, on the other hand, are numbers that are divisible only by 1 and themselves, and cannot be expressed as the product of any other numbers.
The prime factors of 24 are 2, 2, and 3. We can factorize 24 as 2 × 2 × 2 × 3 or 2^3 × 3. Here, 2 and 3 are both prime numbers, but they are not factors of 24 in isolation. They are only prime factors of 24 when combined in the manner shown.
This fact highlights an important concept in number theory: the uniqueness of prime factorization. Every composite number can be expressed as a unique product of prime numbers. This fundamental theorem of arithmetic is crucial in many areas of mathematics, including cryptography, where it is used to secure communications and protect sensitive information.
In summary, there are no factors of 24 that are prime numbers. However, the prime factors of 24 are 2 and 3, which combine to give the unique prime factorization of 24 as 2^3 × 3.
To know more about prime factorization click here:
brainly.com/question/29763746
#SPJ4
For tax and accounting purposes, corporations depreciate the value of equipment each year. One method used is called "linear depreciation," where the value decreases over time in a linear manner. Suppose that two years after purchase, an industrial milling machine is worth $710,000, and five years after purchase, the machine is worth $180,000.
Required:
Find a formula for the machine value V (in thousands of dollars) at time t ≥ 0 after purchase.
Answers
The formula for the machine value V (in thousands of dollars) at time t ≥ 0 after purchase is given as follows: V (t) = Ct - rt, where C is the initial cost of the machine in thousands of dollars, r is the depreciation rate per year, and t is the time in years since the machine was purchased. V(t) = 710 - 13.7925t Answer: V(t) = 710 - 13.7925t
The value of an industrial milling machine after two years of purchase is $710,000 and after five years, the value is $180,000. Let us find the depreciation rate of the machine.
Linear Depreciation Method: Linear depreciation method is one of the methods used to calculate depreciation in accounting. It is also called straight-line depreciation. Under this method, the depreciation expense of an asset is the same for each year of its useful life.
The formula to calculate the depreciation expense using the straight-line depreciation method is:Depreciation Expense = (Cost of Asset - Salvage Value)/Useful Life Let,
The cost of the industrial milling machine = C = 710The value of the industrial milling machine after five years = S = 180The useful life of the machine in years = LWe have to find a formula for the machine value V (in thousands of dollars) at time t ≥ 0 after purchase.
To find the useful life of the machine, use the following formula:Cost of Asset = Depreciation Expense x Useful Life + Salvage Value710 = (710 - 180)/L * L + 180
Simplifying the above equation, we get:710 = 530/L + 180Multiplying both sides of the equation by L and then subtracting 180 from both sides, we get:530L = 530L = 530 - 180L = 350/53.
Therefore, useful life, L = 350/53 yearsThe depreciation rate of the industrial milling machine is the difference between its cost and salvage value divided by its useful life.
Using the given information, the cost of the machine and the value of the machine after five years, we get: Depreciation Rate = (Cost of Machine - Salvage Value) / Useful LifeDepreciation Rate = (710 - 180) / (350/53)Depreciation Rate = 13.7925
Hence, the formula for the machine value V (in thousands of dollars) at time t ≥ 0 after purchase is given as follows:V (t) = Ct - rt, where C is the initial cost of the machine in thousands of dollars, r is the depreciation rate per year, and t is the time in years since the machine was purchased. V(t) = 710 - 13.7925t Answer: V(t) = 710 - 13.7925t
Learn more on depreciation here:
brainly.com/question/30531944
#SPJ11
I need help!!!!!!What is the average rate of change of g over the interval – 4 < t < 1?
Give an exact number.
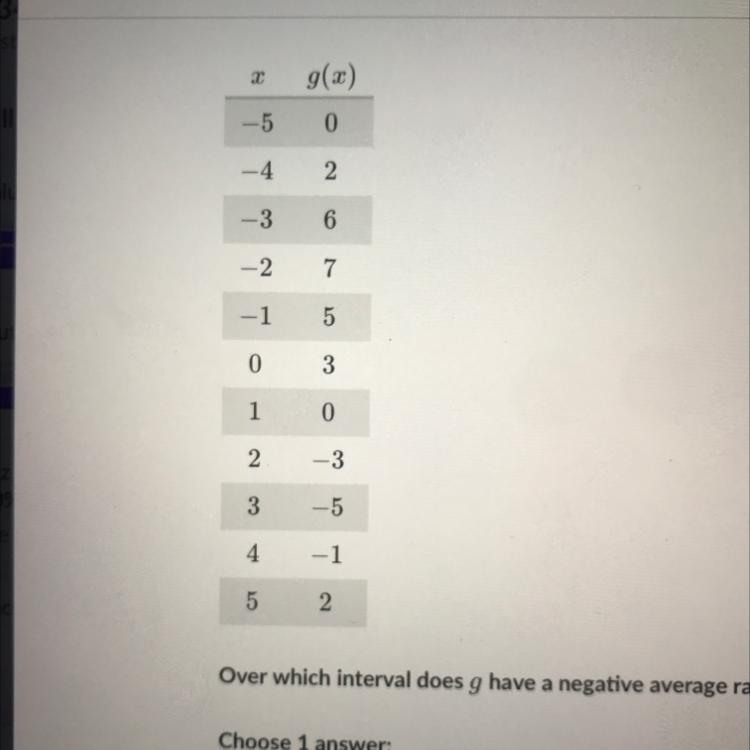
Answers
Answer:
-0.4.
Step-by-step explanation:
Average rate of change = difference in g(x) / difference in x
= (0 - 2) / (1 - (-4))
= -2/5 or -0.4.
The average rate of change of g over the interval -4 < t < 1 is -0.4
What is rate of change?
'A rate of change is a rate that describes how one quantity changes in relation to another quantity.'
According to the given problem,
Interval = -4 < t < 1
We know,
rate of change = \(\frac{y_{2}- y_{1} }{x_{2}-x_{1} }\)
y₂ = 0
y₁ = 2
x₂ = 1
x₁ = -4
Rate of change = \(\frac{0-2}{1-(-4)}\)
= \(\frac{-2}{5}\)
= - 0.4
Hence, we can conclude, the average rate of change over the given interval is -0.4.
Learn more about average rate of change here:
https://brainly.com/question/23715190
#SPJ2
For the sequence a_n=3/n+1Find 1st term:Find Second Term:Find third term:Find fourth term:find 100th term:
Answers
Given:
The sequence is
\(a_n=\frac{3}{n+1}\)Required:
Find the first term, the second term, the third term, the fourth term and the 100th term.
Explanation:
The given sequence is:
\(a_{n}=\frac{3}{n+1}\)Substitute n = 1
\(\begin{gathered} a_1=\frac{3}{1+1} \\ a_1=\frac{3}{2} \end{gathered}\)Substitute n = 2
\(\begin{gathered} a_2=\frac{3}{2+1} \\ a_2=\frac{3}{3} \\ a_2=1 \end{gathered}\)Substitute n = 3
\(\begin{gathered} a_3=\frac{3}{3+1} \\ a_3=\frac{3}{4} \end{gathered}\)Substitute n = 4
\(\begin{gathered} a_4=\frac{3}{4+1} \\ a_4=\frac{3}{5} \end{gathered}\)The term of the sequence are:
\(\frac{3}{2},1,\frac{3}{4},\frac{3}{5}\)The given series is in HP
We will write it in AP as:
\(\frac{2}{3},1,\frac{4}{3},\frac{5}{3}\)So the common difference of the given sequence is:
\(\begin{gathered} 1-\frac{2}{3}=\frac{1}{3} \\ \frac{4}{3}-1=\frac{1}{3} \\ \frac{5}{3}-\frac{4}{3}=\frac{1}{3} \end{gathered}\)The nth term of the AP series is given by the formula:
\(a_n=a+(n-1)d\)where a = first term
n = number of terms
d = common difference
\(\begin{gathered} a_{100}=\frac{2}{3}+(100-1)\times\frac{1}{3} \\ a_{100}=\frac{2}{3}+99\times\frac{1}{3} \\ a_{100}=\frac{2+99}{3} \\ a_{100}=\frac{101}{3} \end{gathered}\)This is the 100th term for the AP.
The 100th term of the given HP sequence is:
\(\frac{3}{101}\)Final Answer:
\(\begin{gathered} First\text{ term = }\frac{3}{2} \\ Second\text{ term = 1} \\ Third\text{ term = }\frac{3}{4} \\ Fourth\text{ term = }\frac{3}{5} \\ 100th\text{ term = }\frac{3}{101} \end{gathered}\)in the figure below, lines m and n are parallel. What is the value of x?

Answers
Answer:
x = 51
Step-by-step explanation:
It looks like alt int. angles (correct me if im wrong)
3x - 40 = 2x + 11
x = 51
Solve for x and graph the solution on the number line below.
1≥-x-1 and -x-1≥ −13

Answers
The solution to both inequality is 2 ≥ -x and -x≥ 14
How to calculate inequality ?The idea of inequality, which is the state of not being equal, especially in terms of status, rights, and opportunities1, is at the core of social justice theories. However, because it frequently has diverse meanings to different people, it is prone to misunderstanding in public discourse.
We have the equation 1≥-x-1 and -x-1≥ −13
Let us solve the inequality
1 ≥ - x - 1
1 + 1 ≥ -x
2 ≥ -x
Now, let us solve the inequality
-x-1≥ −13
-x+13 ≥ -1
-x≥ 14
Therefore the solution to both inequality is 2 ≥ -x and -x≥ 14
To learn more about inequality refer to :
https://brainly.com/question/24372553
#SPJ1
need help.................

Answers
Answer:
10218.75
Step-by-step explanation:
You should divide the two shapes into a rectangle and a triangle, find the area of each, then add them together like so:
For the rectangle:
37.5*22.5 = 843.75
For the triangle:
To find the base: 75 - 37.5 = 37.5
To find the height, use pythagoream theorem.
62.5² = 37.5² + b²
3906.25 = 1406.25 + b²
3906.25 - 1406.25 = 2500
√2500 = 50.
The height is 50, so 50*37.5(1/2)
= 937.5
Now add them together
937.5 + 843.75
What is the value of s?

Answers
Answer: 76.3°
Step-by-step explanation:
Opposite angles are equal, or you can say, vertically opposite angles are equal.
Mike has an adjusted gross income of $85,643. He claims two exemptions and can deduct $896 for state income tax, $2,145 for charitable donations, and $3,473 for medical expenses. If the standard deduction is $5,700 and exemptions are each worth $3,650, what is Mike’s total taxable income? a. $72,643 b. $75,479 c. $71,829 d. $66,129 Please select the best answer from the choices provided A B C D.
Answers
Answer:
The answer would be C. $71,829
Hope this helped :D
The net salary after all deductions will be $66,129 and can be calculated by subtraction of gross salary from all deductions thus option (d) is correct.
What is subtraction?To subtract in mathematics is to take something away from a group or a number of objects.
In other meaning, subtraction is a mathematical operation such that two values are going to subtract and give a resultant value.
The group's total number of items decreases or becomes lower when we subtract from it.
Gross income = $85,463
Deductions are,
Income will be $896
Exemptions is 2 x $3,650
Charitable donations is $2,145
Exemptions is 2 x $3,650 expenses is $3,473
Add all above the deduction to find out the total deduction,
$896 + $2,145 + $3,473 + 2 x $3,650 = $13,814
Thus, net income will be as by subtraction,
$85,463 - $13,814 = $66,129
Hence "The net salary after all deductions will be $66,129 and can be calculated by subtraction of gross salary from all deductions".
For more about subtraction,
https://brainly.com/question/1927340
#SPJ6
the distance from city a to city b is 256.8 miles. the distance from city a to city c is 739.4 miles how much farther is the trip to city c than the trip to city b
Answers
Taking a difference, we can see that the trip to city C is 482.6 mi longer.
How much farther is the trip to city c than the trip to city b?
Here we know that the distance from city a to city b is 256.8 miles, and the distance from city a to city c is 739.4 miles
To find how much farther is the trip to city c than the trip to city b, we just need to take the difference between the two distances above.
That means that we need to take the distance to city c and subtract the distance to city b.
We will get:
739.4 mi - 256.8 mi = 482.6 mi
The trip to city C is 482.6 mi more than the trip to city B.
Learn more about differences at:
https://brainly.com/question/17695139
#SPJ1
Pretty please answer asap! thank you so much for your time <333
:D

Answers
Answer:
B
Step-by-step explanation:
Two lines are perpendicular if and only if the product of their slopes is . In other words, the slope of a line that is perpendicular to a given line is the negative reciprocal of that slope. Thus, for a line with a given slope of 3, the line perpendicular to that slope must be the negative reciprocal of 3, or .
Answer:
B
Step-by-step explanation:
B because the slope/ gradient is -1/2, which is the reciprocal of the equation's gradient that we have, which is 2.
Did I do this right? Tell me

Answers
There are 15 pieces of fruit in a bowl and 9 of them are apples. What percentage of the pieces of fruit in the bowl are apples?
Answers
Answer:
9 divided by 100 = 0.09 x 15 = 1.35 = 13%
PLs mark me brainliest
Answer:
60%
Step-by-step explanation:
You can first convert 9 out of 15 into 9/15. Then, you can find the percent of 9/15, which is 60% :)
~Happy Halloween!~
one fruitloops are gay 2 what is 8=-4+x please and thank you
Answers
Answer:
Okayyy.... anywayss...
Solve for x by simplifying both sides of the equation, then isolating the variable.
x = 12
Step-by-step explanation:
I hope that this answer helps you to understand your question asked. If you have any further questions, please ask them below.
Have a great rest of your day/night!
At which root does the graph of f x x 5 3 * x 2 2 touch the X axis?
Answers
The root of the graph of f(x) =(x - 5)3(x + 2)2 touches the x-axis at -2,5
(x - 5)^3 has a power of 3 which is an ODD number. An ODD power means that the graph will cross through the x-axis.
(x + 2)^2 has a power of 2 which is an EVEN number. An EVEN power means that the graph will touch the x-axis.
Given: Function f(x) is (x - 5)3(x + 2)2
If a curve touches the x-axis then f(x) = 0
⇒ (x - 5)3(x + 2)2 = 0.
But if ab = 0 ⇒ either a = 0 or b = 0 or both zero.
⇒ (x - 5)3 = 0 and (x + 2)2 = 0
⇒ (x - 5) = 0 and x + 2 = 0
⇒ x = 5 and x = - 2.
To know more about the roots of functions:
https://brainly.com/question/1942920
#SPJ4

1 out of 8 students likes cats more than dogs. Write this amount as a decimal.
Answers
Answer:
12.5
Step-by-step explanation:
100.0 ÷ 8.0 = 12.5
wjksjz
Answer:
125
Step-by-step explanation:
To convert 1/8 to a decimal, divide the denominator into the numerator. 1 divided by 8 = . 125. To convert the decimal .
the current tempurure out side is -3 how many degress would you have to add to make it five degress
Answers
Answer:
8 degree
Step-by-step explanation:
-3+x=5
x=5+3=8 degree
Question 4 of 10
The standard form of the equation of a parabola is y=x²-6x+14.
What is the vertex form of the equation?
OA y=(x-3)2 +15
OB. y = (x+3)(x-3) +5
O C. y=(x-3)2 +23
OD. y=(x-3)² +5
Answers
The vertex form of the equation is y = (x - 3)² - 4, which corresponds to option OD.
To convert the given equation from standard form to vertex form, we need to complete the square.
The vertex form of a parabola's equation is y = a(x-h)² + k, where (h, k) represents the vertex of the parabola.
Given equation: y = x² - 6x + 14
Move the constant term to the right side:
y - 14 = x² - 6x
Complete the square by adding and subtracting the square of half the coefficient of x:
y - 14 + 9 = x² - 6x + 9 - 9
Group the terms and factor the quadratic:
(y - 5) = (x² - 6x + 9) - 9
Rewrite the quadratic as a perfect square:
(y - 5) = (x - 3)² - 9
Simplify the equation:
y - 5 = (x - 3)² - 9
Move the constant term to the right side:
y = (x - 3)² - 9 + 5
Combine the constants:
y = (x - 3)² - 4
For similar question on vertex.
https://brainly.com/question/1217219
#SPJ8
Among college students, the proportion p who say they're interested in their congressional district's election results has traditionally been 65%. After a series of debates on campuses, a political scientist claims that the proportion of college students who say they're interested in their district's election results is more than 65%. A poll is commissioned, and 180 out of a random sample of 265 college students say they're interested in their district's election results. Is there enough evidence to support the political scientist's claim at the 0.05 level of significance?
Answers
Using the test statistic, at the 0.05 level of significance, we do not find sufficient evidence to support the political scientist's claim and hence reject the null hypothesis.
Do we have enough evidence to support the political scientist's claim at the 0.05 level of significance?To determine whether there is enough evidence to support the political scientist's claim that the proportion of college students interested in their district's election results is more than 65%, we can perform a hypothesis test using the given data.
Let's set up the null and alternative hypotheses:
H₀: p ≤ 0.65 (Null hypothesis: The proportion of college students interested in election results is 65% or less)
Ha: p > 0.65 (Alternative hypothesis: The proportion of college students interested in election results is more than 65%)
We are given that the sample size is 265 college students, and out of this sample, 180 students say they're interested in their district's election results.
To perform the hypothesis test, we'll calculate the test statistic, which is the z-statistic in this case, using the formula:
z = (p - p₀) / √(p₀(1-p₀)/n)
Where p is the sample proportion, p₀ is the hypothesized proportion under the null hypothesis, and n is the sample size.
Let's calculate the sample proportion:
p = 180 / 265 ≈ 0.679
Now, we can calculate the test statistic:
z = (0.679 - 0.65) / √(0.65(1-0.65)/265) ≈ 1.295
Next, we'll compare the test statistic with the critical z-value at a 0.05 level of significance (α = 0.05) for a one-tailed test.
Using a standard normal distribution table or a statistical calculator, the critical z-value at α = 0.05 is approximately 1.645.
Since the test statistic (1.295) does not exceed the critical z-value (1.645), we fail to reject the null hypothesis. In other words, we do not have enough evidence to support the political scientist's claim that the proportion of college students interested in their district's election results is more than 65% based on this sample.
Learn more on null hypothesis here;
https://brainly.com/question/25263462
#SPJ4
What is 5a+2.4(a+0.5b)−0.2b
Answers
Answer: 7.4a+b
1. distribute
=5a+(2.4)(a)+(2.4)(0.5b)+−0.2b
=5a+2.4a+1.2b+−0.2b
2. combine like terms
=5a+2.4a+1.2b+−0.2b
=(5a+2.4a)+(1.2b+−0.2b)
=7.4a+b
What is –70 divided by 700
PLZ HELP ME!!!
Answers
Answer: -0.1
Step-by-step explanation: Calculator
Hello!
-70 : 700 = -0,1 → answer
Good luck! :)
the activity of a radioactive isotope is found to decrease by 40% in one week. what are the values of its: a) decay constant, b) half-life, c) mean lifetime?
Answers
Answer: A) The decay constant (λ) is a measure of the rate at which a radioactive isotope decays. It is defined as the probability per unit time that an atom of the isotope will decay. The decay constant can be calculated using the formula:
λ = -ln(1 - x) / t
Where x is the fraction of the original activity that has decayed (in this case, 0.40), and t is the time over which the decay occurred (in this case, one week).
B) The half-life (T1/2) is the amount of time it takes for half of the original activity of a radioactive isotope to decay. It can be calculated using the formula:
T1/2 = ln(2) / λ
C) The mean lifetime (τ) is the average amount of time an atom of a radioactive isotope will survive before it decays. It can be calculated using the formula:
τ = 1 / λ
It's important to note that the above formulas are based on the exponential decay model, which assumes that the decay process is random and that the decay constant is constant over time. If the isotope does not decay in this way, these formulas may not give accurate results.
Step-by-step explanation:
Image transcription text(24 points) Prove whetehr the following systems are causal, time invariant or linear. (a) y(t) = 133:0?) + 2:05 — 2).
(b) y(t) + dad—g" = 11:03) + 33(t — 1). ... Show more
Answers
(a) The system described by the equation y(t) = 133x(t) + 2.05 - 2 is linear and time-invariant but not causal.
To determine linearity, we check if the system satisfies the superposition property. Given inputs x1(t) and x2(t) with corresponding outputs y1(t) and y2(t), let's denote the system as H. We have:
H[x1(t) + x2(t)] = 133[x1(t) + x2(t)] + 2.05 - 2 = 133x1(t) + 133x2(t) + 2.05 - 2
On the other hand, H[x1(t)] + H[x2(t)] = (133x1(t) + 2.05 - 2) + (133x2(t) + 2.05 - 2) = 133x1(t) + 133x2(t) + 2.05 - 2
Since H[x1(t) + x2(t)] = H[x1(t)] + H[x2(t)], the system satisfies the superposition property and is linear.
To determine time-invariance, we check if a time shift in the input results in an equivalent time shift in the output. Let's consider a time shift δ:
H[x(t - δ)] = 133x(t - δ) + 2.05 - 2
If we compare this to the original equation y(t) = 133x(t) + 2.05 - 2, we can see that the shift δ is applied in both cases. Therefore, the system is time-invariant.
To determine causality, we need to check if the output y(t) depends only on the past and present values of the input x(t). In this case, we see that the output y(t) depends on the future value x(t + 1) due to the term 2. Therefore, the system is not causal.
The system described by y(t) = 133x(t) + 2.05 - 2 is linear, time-invariant, but not causal.
To know more about equation follow the link:
https://brainly.com/question/29718677
#SPJ11
Describe the sampling distribution of p. Assume the size of the population is 30,000. n=900, p=0.532 Describe the shape of the sampling distribution of p. Choose the correct answer below. OA The shape
Answers
The normal approximation to the binomial distribution also implies that the sampling distribution of p is roughly bell-shaped, as the normal distribution is. Therefore, the answer is A) The shape.
The sampling distribution of the proportion is the distribution of all possible values of the sample proportion that can be calculated from all possible samples of a certain size taken from a particular population in statistical theory. The state of the examining dispersion of p is generally chime molded, as it is an illustration of a binomial conveyance with enormous n and moderate p.
The example size (n=900) is sufficiently enormous to legitimize utilizing an ordinary guess to the binomial dissemination, as indicated by as far as possible hypothesis. In order for the binomial distribution to be roughly normal, a sample size of at least 30 must be present, which is achieved.
Subsequently, the examining dispersion of p can be thought to be around ordinary with a mean of 0.532 and a standard deviation of roughly 0.0185 (involving the equation for the standard deviation of a binomial distribution).The typical estimate to the binomial dissemination likewise infers that the inspecting conveyance of p is generally chime molded, as the ordinary circulation is. As a result, A) The shape is the response.
To know more about standard deviation refer to
https://brainly.com/question/12402189
#SPJ11
Anyone know the answer?

Answers
Answer:
Step-by-step explanation:
(21 + 3y) + y = 90
21 + 4y = 90
4y = 69
y = 17.25
x = 21 + 3(17.25)
x = 21 + 51.75
x = 72.75
Answer check:
72.75 + 17.25 = 90
90 = 90 Corrrrrrect !
Explanation:
x = 3y + 21
And x + y = 90° (complementary angle)
Substitute x value in the equation:
3y + 21 + y = 90
4y + 21 = 90
4y = 69
y = 69/4
y = 17.25
x = 3(17.25) + 21
x = 51.75 + 21
x = 72.75
Jasmin's dog weighs 55 pounds. Her vet told her that a healthy weight for her dog would be less than or equal to 41 pounds.
Jasmin's dog can lose an average of 0.5 pounds every week. Write the solution to an inequality that describes all possible number of
weeks 2 for which her dog can be at a healthy weight.
Answers
Answer:
55-0.5x ≤ 41 (x will represent the weeks)
Step-by-step explanation:
i made x represent the weeks and we know that jasmin's dog can lose about 0.5 pound a week. and the base is 55 lbs since that is what jasmin's dog weighs. 55 minus all the weight that jasmin's dog will lose in a certain amount of weeks is the first part. then we know jasmin's dog has to be less than or equal to 41 lbs. so put that there with the less than or equal to sign.
i need help please thanks

Answers
Answer:
Use Symbolab i think thats how you spell it
Step-by-step explanation:
Shelby made equal deposits at the beginning of every 3 months into an RRSP. At the end of 9 years, the fund had an accumulated value of $55,000. If the RRSP was earning 3.50\% compounded monthly, what was the size of the quarterly deposits? Round to the nearest cent
Answers
The size of the quarterly deposits in Shelby's RRSP account was approximately $147.40.
Let's denote the size of the quarterly deposits as \(D\). The total number of deposits made over 9 years is \(9 \times 4 = 36\) since there are 4 quarters in a year. The interest rate per period is \(r = \frac{3.50}{100 \times 12} = 0.0029167\) (3.50% annual rate compounded monthly).
Using the formula for the future value of an ordinary annuity, we can calculate the accumulated value of the RRSP fund:
\[55,000 = D \times \left(\frac{{(1 + r)^{36} - 1}}{r}\right)\]
Simplifying the equation and solving for \(D\), we find:
\[D = \frac{55,000 \times r}{(1 + r)^{36} - 1}\]
Substituting the values into the formula, we get:
\[D = \frac{55,000 \times 0.0029167}{(1 + 0.0029167)^{36} - 1} \approx 147.40\]
Therefore, the size of the quarterly deposits, rounded to the nearest cent, is approximately $147.40.
To learn more about interest Click Here: brainly.com/question/30393144
#SPJ11