Base perimeter of a square prism is 32cm and its height is 15cm. what is its
lateral surface area?
Answers
\(\large\bf{\underline{Correct\: question}}\)
Base perimeter of a square pyramid is 32cm and its height is 15cm. what is its lateral surface area?__________________________________________
\(\large\bf{\underline{Given : }}\)
Base perimeter of square pyramid = 32 cm \(\large\bf{⟹ Base\: side =\frac{32}{4}=8 cm}\)
height of pyramid = 15 cm__________________________________________
\(\large\bf{\underline{Lateral\: surface\:area :}}\)
\(\large\boxed{4 \times \frac{1}{2} \times base \: \times height}\)
\( = 4 \times \frac{1}{2} \times 8 \times 15\)
\( = 240 {cm}^{2} \)
__________________________________________
\(\large\bf{\underline{Hence, L.S.A }}\)
\(\large\bf{ = 240 {cm}^{2}}\)
Related Questions
Identify the sampling technique used in each study. Explain your reasoning. (a) A journalist goes to a campground to ask people how they feel about air pollution (b) For quality assurance, every tenth machine part is selected from an assembly line and measured for accuracy. (c) A study on attitudes about smoking is conducted at a college. The students are divided by class (freshman, sophomore, junior, and senior). Then a random sample is selected from each class and interviewed.
Answers
The sampling technique used in each study is as follows: (a) convenience sampling, (b) systematic sampling, and (c) stratified random sampling.
(a) In the first study, where a journalist goes to a campground to ask people about their feelings regarding air pollution, the sampling technique used is convenience sampling. This is evident because the journalist approaches individuals who are readily available and easily accessible at the campground. However, convenience sampling may introduce bias as it does not ensure a representative sample of the population.
(b) In the second study, where every tenth machine part is selected from an assembly line for measurement, the sampling technique used is systematic sampling. Systematic sampling involves selecting every nth element from a population after establishing a sampling interval. In this case, every tenth machine part is selected to ensure a systematic and unbiased approach to quality assurance.
(c) In the third study, where attitudes about smoking are studied at a college and students are divided by class and then randomly sampled from each class for interviews, the sampling technique used is stratified random sampling. Stratified random sampling involves dividing the population into homogeneous subgroups (strata) and then randomly selecting samples from each subgroup. By dividing the students into different class strata and randomly selecting samples from each class, this study aims to ensure representation from each class in the final sample.
Learn more about sampling technique here:
https://brainly.com/question/31697553
#SPJ11
helppppppppppppppppppppppppppppppppppppppppppppppp

Answers
Answer:
Option D
Step-by-step explanation:
Area of triangle = \(\frac{1}{2}\) × (Base of triangle) × (Perpendicular height of triangle)
= \(\frac{1}{2}\) × [(20 - 10) inches] × [(15 - 5) inches]
= \(\frac{1}{2}\) × (10 inches) × (10 inches)
= 50 square inches
∴Area of each triangular piece = 50 square inches
∴Option D
An experiment consists of dealing 5 cards from a standard 52-card deck. What is the probability of being dealt a 3, 4, 5, 6, 7, all in the same suit? The probability of being dealt a 3, 4, 5,6, 7, all in the same suit is Round to seven decimal places as needed.)
Answers
The probability of being dealt a 3, 4, 5, 6, 7, all in the same suit is approximately 0.0000031.
To calculate the probability of being dealt a 3, 4, 5, 6, 7, all in the same suit, we can use the following formula:
P = (number of favorable outcomes) / (total number of possible outcomes)
the order in which the cards are chosen does not matter, so we need to divide by the number of ways we can arrange 5 cards, which is 5! (5 factorial).
Therefore, the total number of possible outcomes is (52 * 51 * 50 * 49 * 48) / (5 * 4 * 3 * 2 * 1), which simplifies to 2,598,960.
Finally, we can calculate the probability of being dealt a 3, 4, 5, 6, 7, all in the same suit:
P = 8 / 2,598,960
P = 0.00000308 (rounded to seven decimal places)
To know more about Probability:
https://brainly.com/question/30034780
#SPJ4
3.
15 In.
25 in.
a ft

Answers
the value of the side a will be 20feet.
What is Pythagoras theorem?
The Pythagoras theorem says that if a triangle has a straight angle (90 degrees), the square of the hypotenuse is equal to the sum of the squares of the other two sides. To illustrate this, the triangle ABC has the formula BC2 = AB2 + AC2. This equation includes the bases AB, height AC, and hypotenuse BC. It is important to note that the hypotenuse is the right-angled triangle's longest side.
h²=b²p²
b²=25²-15²
b²=675-215
b=√400
b=20 feet
Hence, the value of the side a will be 20feet.
Learn more about Pythagoras theorem, by the following link
https://brainly.com/question/231802
#SPJ1
Convert meters to centimeters. 9.2 m = afers x 1. cm m) cm)
Answers
7. Emily and John will be hiking for 42 hours. Hikers should drink at least 2.7 cups of water for every 2 hours of hiking. How many cups of water should Emily and John drink?
Answers
Step-by-step explanation:
in 24 hours they will drink 32.7 cups
in 18 hours they will drink 24.3
32.7+24.3=56.7
16 less than the product of - 2 and -12
Answers
Answer:
8
Step-by-step explanation:
-12 x -2 = 24. 24-16=8
Table 3.1 Quantity Demanded Price per Unit Quantity Supplied 10 $5 50 20 $4 40 30 $3 30 40 $2 20 50 $1 10 Refer to Table 3.1. If the government imposes a price of $2, O a surplus equal to 20 units wil
Answers
Referring to Table 3.1, if the government imposes a price of $3, a shortage will result.
To determine the outcome when the government imposes a price of $3, we need to compare the quantity demanded and quantity supplied at this price level.
According to Table 3.1, at a price of $3, the quantity demanded is 30 units, while the quantity supplied is 40 units. The quantity demanded (30 units) is less than the quantity supplied (40 units), resulting in a situation known as a shortage.
A shortage occurs when the quantity demanded exceeds the quantity supplied at a given price. In this case, a shortage of 10 units occurs because consumers are willing to buy more than what producers are offering at the price of $3.
To summarize, if the government imposes a price of $3 based on Table 3.1, a shortage will result. This means that the quantity demanded exceeds the quantity supplied at the given price, indicating that consumers are unable to purchase all the units they desire.
Learn more about price here
https://brainly.com/question/19091385
#SPJ11
the complete question is:
Table 3.1
Quantity Demanded.
Price per Unit
Quantity supplied
10
$5
50
20
30
$4
$3
40
30
40
50
$2
$1
20
10
Refer to Table 3.1. If the government imposes a price of $3.
a shortage will result.
Market is in equilibrium.
the price will fall to $1 because producers will be forced to incur losses.
a surplus will result.
Stone runs 1 mile five times a week. How many miles does 4 he run each week? Write the equation you would use to solve. Then, fill in the grid with your answer. Tip: Fill in your answer as a fraction greater than 1.
Answers
The number of miles in 4 weeks is 20 mules
How to determine the number of milesFrom the question, we have the following parameters that can be used in our computation:
Stone runs 1 mile five times a week
This means that the rate is
Rate = 1 mile * 5 per week
So, we have
Rate = 5 miles per week
For 4 weeks, we have
Distance = 5 * 4
Evaluate
Distance = 20 miles
Hence, the distance is 20 miles
Read more about rate at
https://brainly.com/question/24178013
#SPJ1
4. Prove that (a) A\B=AANB)
Answers
Any element x satisfying either condition belongs to both sets, we can conclude that (A\B) = A ∩ (A ∪ B).
To prove that (A\B) = A ∩ (A ∪ B), we need to show that the sets have the same elements.
Let's consider an element x:
1. Suppose x ∈ (A\B), which means x is in A but not in B.
- This implies that x ∈ A (since x is in A) and x ∉ B (since x is not in B).
- Since x ∈ A, it is also in the union A ∪ B.
- Since x ∉ B, it is not in the intersection A ∩ B.
- Therefore, x ∈ A ∩ (A ∪ B) since it is in A and not in the intersection A ∩ B.
2. Suppose x ∈ A ∩ (A ∪ B), which means x is in both A and (A ∪ B).
- This implies that x ∈ A and x ∈ (A ∪ B).
- Since x ∈ (A ∪ B), it is either in A or in B (or both).
- Since x ∈ A, it is not in the complement of A, which means it is not in B.
- Therefore, x ∈ (A\B) since it is in A and not in B.
Since we have shown that any element x satisfying either condition belongs to both sets, we can conclude that (A\B) = A ∩ (A ∪ B).
Learn more about sets from :
https://brainly.com/question/13458417
#SPJ11
A bag contains 9 green marbles and 12 white marbles. In simplest form, what are the odds in favor of drawing a white marble?
A) 4:7
B) 4:3
C) 1:7
D) 3:4

Answers
Answer:
3 : 4, D
Step-by-step explanation:
Since the ratio is 9 : 12, simply put it in fraction form and simplify.
Find the gradient of the line segment between the points (2,5) and (1, -6)
Answers
Multiply 2 to the odd position number then adding -4 to the even position number stating 3. ( complete the number pattern
__,__,__,__,__,__,__,__,__,__
Answers
A complete list of the numbers in the pattern: 3, 6, 10, 14, 18, etc.
How to calculate the valueThe number pattern you described is as follows:
3,
(2*5)-4 = 6,
(2*7)-4 = 10,
(2*9)-4 = 14,
(2*11)-4 = 18,
The first number is 3, and then each subsequent number is found by multiplying the previous odd number by 2 and then subtracting 4.
For example, the second number is found by multiplying the first number by 2 and then subtracting 4, which gives us 6. The third number is found by multiplying the second number by 2 and then subtracting 4, which gives us 10.
Learn more about numbers on
https://brainly.com/question/25734188
#SPJ1
what is 76.385 + 8.93
Answers
Hope this helps!!!
2/3 X 3/4 please helppppp
Answers
2/3 x 3/4
You multiply the numerators by each other (top numbers) and the denominators by each other (bottom numbers)
2x3=6
3x4=12 so it would be 6/12 which simplifies ( divided by 2) to 1/2
What is the slope of the line tangent to the curve y^3-xy^2+x^3=5 at the point (1,2)?
Options are as follows: A. 1/10
B. 1/8
C. 5/12
D. 11/4
Answers
The slope of the line tangent to the curve y³-xy²+x³=5 at the point (1,2) is option (B) 1/8.
To find the slope of the line tangent to the curve at the point (1,2), we first need to find the derivative of the curve with respect to x, and then evaluate it at x=1, y=2.
Taking the derivative of both sides of the equation y³-xy²+x³=5 with respect to x using the product rule, we get
3y²(dy/dx) - y² - 2xy(dy/dx) + 3x² = 0
Simplifying this expression and solving for dy/dx, we get:
dy/dx = (y² - 3x²)/(3y² - 2xy)
Substituting x=1 and y=2, we get:
dy/dx = (2² - 3(1)²)/(3(2)² - 2(1)(2))
dy/dx = (4 - 3)/(12 - 4)
dy/dx = 1/8
Therefore, the correct option is (B) 1/8
Learn more about slope here
brainly.com/question/30577296
#SPJ4
13) A hexagon has 6 equal sides! Ms. Sears asked the students to find the perimeter if all sides are equal to 2x + y. One student found the solution to be 18xy and another thinks it is 9xy. Is either solution correct? Show your work to justify your answer.
Answers
Answer:
None of the answers are right
Step-by-step explanation:
Since a hexagon has 6 sides, and perimeter is the length of all the sides summed up, we can multiply 6 by 2x+y to find the perimeter.
6(2x+y)
Distribute the 6 to each term in the parentheses:
6(2x)+6(y)
12x+6y is the perimeter. None of the answers are right.
-8 with power -2/3 iam so confused either answer will be positive or negative? Give solution please hurry up.....
Answers
Answer:
\(\frac{1}{4}\)
Step-by-step explanation:
Using the rule of exponents / radicals
\(a^{\frac{m}{n} }\) = \((\sqrt[n]{a})^m\)
\(a^{-m}\) = \(\frac{1}{a^{m} }\) , then
\(-8^{-\frac{2}{3} }\)
= \(\frac{1}{-8^{\frac{2}{3} } }\)
= \(\frac{1}{(\sqrt[3]{-8})^2 }\)
= \(\frac{1}{-2)^{2} }\)
= \(\frac{1}{4}\)
4. What is the equation of the line that represents your initial climb?

Answers
the feasible corner points are (48,84), (0,120), (0,0), and (90,0). what is the maximum possible value for the objective function?
Answers
In linear programming, the feasible region is the set of all feasible solutions that satisfy the constraints of the problem. The feasible corner points are the extreme points of the feasible region, which represent the optimal solutions to the problem. In this case, we have four feasible corner points: (48,84), (0,120), (0,0), and (90,0).
To find the maximum possible value for the objective function, we need to evaluate the objective function at each of the feasible corner points and select the one that gives the highest value. The objective function is a linear combination of the decision variables and represents the quantity that we are trying to maximize or minimize.
Assuming that the objective function is in the form of z = ax + by, where x and y are the decision variables and a and b are constants, we can evaluate the objective function at each of the feasible corner points:
At (48,84): z = a(48) + b(84)
At (0,120): z = a(0) + b(120)
At (0,0): z = a(0) + b(0)
At (90,0): z = a(90) + b(0)
Since we don't have the values of a and b, we cannot calculate the maximum possible value of the objective function. However, we can compare the values of the objective function at each of the feasible corner points and select the one that gives the highest value.
Therefore, we can conclude that the maximum possible value for the objective function will be obtained at one of the feasible corner points: (48,84), (0,120), (0,0), or (90,0).
For more details about linear click here:
https://brainly.com/question/15830007#
#SPJ11
Please help and show work only do the left side

Answers
Writing linear equations given two points can be a useful skill when graphing linear equations.
Write a linear equation that passes through the given two points?To write a linear equation given two points, you need to first find the slope of the line. You can do this by finding the change in the y-value and dividing it by the change in the x-value. From there, you can use the slope to solve for the y-intercept and write the equation.For example, if the two points are (3, 4) and (0,5), you would find the slope by calculating the change in the y-value (5-4 = 1) and dividing it by the change in the x-value (0-3 = -3).The slope would then be 1/-3, which can be simplified to -1/3. To solve for the y-intercept, you can plug in one of the points and solve for b. In this case, you would plug in (3, 4) and solve for b, giving you b = 5. Now that you have the slope and y-intercept, you can write the equation as y = -1/3x + 5.y = -1/2xy = 5/3x + 5/3y = 3/5x + 1y = -1/2x - 2y = 6/5x + 5y = -4/4x - 8y = -3/5x - 7/5y = -2x - 4y = 5/6x + 7y = -1/2x + 4To learn more about linear equation refer to:
https://brainly.com/question/2030026
#SPJ1
Please help ASAP! Ty!

Answers
Answer:
67
Step-by-step explanation:
Answer:
The volume of the gas under these circumstances is 30 cm³.
Step-by-step explanation:
To determine the variation equation for this situation, we start with the formula V = Tk/P
where k is the constant of variation.
To solve for k, we use the initial values of V, T, and P
V = 42 cm³, T = 84 °C, P = 50 mmHg
Substituting these values into the formula, we get
42 = 84k/50
Solving for k, we have
k = (42 x 50)/84 = 25
Therefore, the variation equation for this situation is
V = 25T/P
To find the volume of gas when T = 48 °C and P = 40 mmHg, we substitute these values into the variation equation
V = 25 x 48/40 = 30 cm³
Therefore, the volume of the gas under these circumstances is 30 cm³.
Question 5a (3 pts). Show \( A=\left\{w w: w \in\{0,1\}^{*}\right\} \) is not regular
Answers
The language A, defined as the set of all strings that are repeated twice (e.g., "00", "0101", "1111"), is not regular.
To show that A is not a regular language, we can use the pumping lemma for regular languages. The pumping lemma states that for any regular language, there exists a pumping length such that any string longer than that length can be divided into parts that can be repeated any number of times. Let's assume that A is a regular language. According to the pumping lemma, there exists a pumping length, denoted as p, such that any string in A with a length greater than p can be divided into three parts: xyz, where y is non-empty and the concatenation of xy^iz is also in A for any non-negative integer i. Now, let's consider the string s = 0^p1^p0^p. This string clearly belongs to A because it consists of the repetition of "0^p1^p" twice. According to the pumping lemma, we can divide s into three parts: xyz, where |xy| ≤ p and |y| > 0. Since y is non-empty, it must contain only 0s. Therefore, pumping up y by repeating it, the resulting string would have a different number of 0s in the first and second halves, violating the condition that the string must be repeated twice. Thus, we have a contradiction, and A cannot be a regular language.
Learn more about pumping lemma here:
https://brainly.com/question/33347569
#SPJ11
Evaluate: f(2) if f(x) = 4 - 2x
f(2) = 0
f(2)= 2
f(2)= 4
f(2) = 8
Answers
Answer:
f(2) = 0
Step-by-step explanation:
Evaluate: f(2) if f(x) = 4 - 2x; plug in 2 for x
f(2) = 4 - 2(2) = 4 - 4 = 0
Answer:
f(2) = 0
Step-by-step explanation:
Put 2 in the place of x,
f(2) = 4 - 2(2)
f(2) = 4 - 4
f(2) = 0
Which set of rational numbers are ordered from least to greatest?
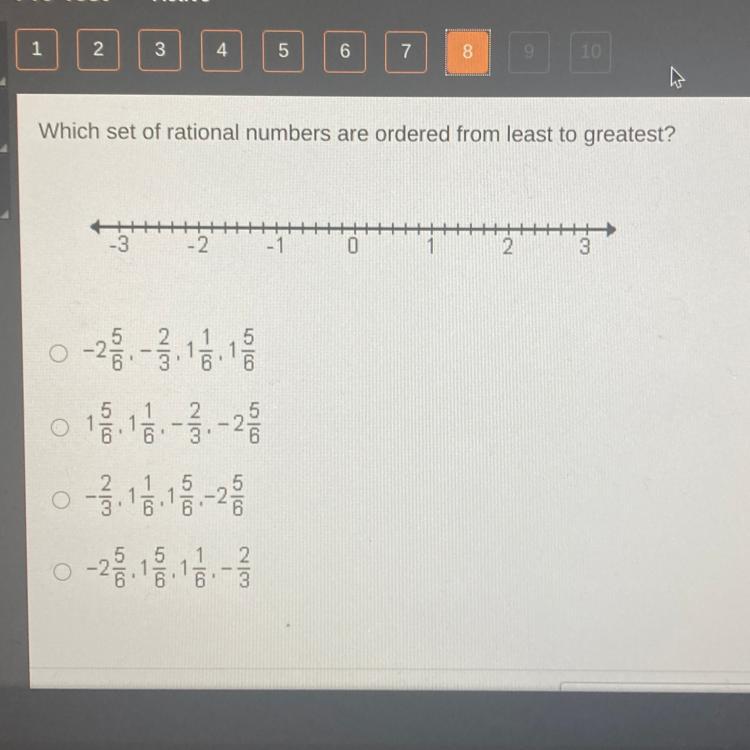
Answers
Answer:
a -25/6 is the least and then -2/3 then 1 1/6 and 1 15/6
A student has a dog and cat for a pet. The dog eats 3 pounds of food
for every 1 pound of food the cat eats. If the pets eat a total of 464
pounds of food combined, how much food did each the cat and dog
eat?
Answers
Answer:
I'm not reallu sure.. but 5
Step-by-step explanation:
Want free points?! Want free brainliest?! Come to my profile and just answer one of my questions. I am YOUR community builder who gives free things. ("Thanks" on ur profile, points, hacks, brainliest, etc.)
Put me as brainliest so I can receive 50% more points!
SOMEONE HEELLPPPP PLEASEEEEEEEEE !!!!!!

Answers
Answer:
The second answer, 7y - 4x =12 would make the system have no solution.
5. A theater wants to take in at least $2000 for the matinee. Children's
tickets cost $5 each and adult tickets cost $10 each. The theater can seat
up to 350 people. Select all the combinations of children and adult tickets
that will make the $2000 goal.
There are several possible answers.
A- (80, 150)
B- (40, 200)
C- (60, 150)
D- (70, 160)
E- (90, 200)
F- (200, 100)
Answers
The required number of children and adults for sitting in the theater are 300 and 50 respectively.
Explain linear equation of two variable.A equation is supposed to be linear equation in two factors in the event that it is written as hatchet + by + c=0, where a, b and c are genuine numbers and the coefficients of x and y, i.e an a and b separately, are not equivalent to nothing. For instance, 10x+4y = 3 and - x+5y = 2 are straight equation in two factors.
According to question:Let be consider number of children be x and that of adults is y.
We have,
x + y = 350-------(1)
y = 350 - x
And 5x + 10y = 2000------------------(2)
Put value of y in equation (2)
5x + 10( 350 - x) = 2000
5x + 3500 - 10x = 2000
-5x = -1500
x = 300
Then
y = 350 - x = 350 - 300 = 50
Thus, There will be 300 children and 50 adults in the theater .
To know more about equation of two variable visit:
brainly.com/question/29209545
#SPJ1
when one finds what percent one number is of another we look for the
A.percentage
B.rate
C.base
D.ratio
Answers
Answer: A is the answrr. Percentage
Step-by-step explanation:
Answer:
the correct awnser is B we look for the rate
Does this equation y=87.2/x represent a direct or inverse variation?
Answers
Answer:
Inverse relationship
Step-by-step explanation:
The equation we are looking at is;
y = 87.2/x
which implies xy = 87.2
If it was a direct relationship
y = constant * x
if it was inverse, it would have been
y * x = constant
since 87.2 is a constant, the question looks exactly like the second scenario.
This means that what we have is an inverse relationship