Answers
Related Questions
⦁ In a class of 25 children there are 10 girls. What percentage of the class are girls and what percentage are boys?
Answers
Answer:
Girls ---> 40% Boys ----> 60%
Step-by-step explanation:
It is given 10 are girls, which logically implies, 15 are boys.
Now given that the total number of children in the class is 25,
Percentage of girls = 10/25 x 100 = 40%
You could do the same for boys by doing 15/25 x 100, or use some logic and realise that two sets should have a percentage of 100, therefore the percentage of boys in the class is 60%
The data on the right represent the number of live multiple-delivery births (three or more babies) in a particular year for women 15 to 54 years old. Use the data to complete parts (a) through (d) below.
Age 15-19 20-24 25-29 30-34 35-39 40 44 45-54 Number of Multiple Births 89 508 1631 2822 1855 374 119 (a) Determine the probability that a randomly selected multiple birth for women 15-54 years old involved a mother 30 to 39 years old P(30 to 39) =______
(Type an integer or decimal rounded to three decimal places as needed.)
(b) Determine the probability that a randomly selected multiple birth for women 15-54 years old involved a mother who was not 30 to 39 years old. P(not 30 to 39)=_____ (Type an integer or decimal rounded to three decimal places as needed.) (c) Determine the probability that a randomly selected multiple birth for women 15-54 years old involved a mother who was less than 45 years old. P(less than 45)=_____
(Type an integer or decimal rounded to three decimal places as needed.) (d) Determine the probability that a randomly selected multiple birth for women 15-54 years old involved a mother who was at least 40 years old. Interpret this result. Is it unusual? Find the probability that a randomly selected multiple birth for women 15-54 years old involved a mother who was at least 40 years old. P(at least 40) =_____ (Type an integer or decimal rounded to three decimal places as needed.) Interpret this result. Select the correct choice below and fill in the answer box to complete your choice. (Type a whole number.) A. If 1000 multiple births for women 15-54 years old were randomly selected, we would expect about of them to involve a mother who was at least 40 years old. B. If 1000 multiple births for women 15-54 years old were randomly selected, exactly of them would involve a mother who was at least 40 years old. Is a multiple birth involving a mother who was at least 40 years old unusual? A. Yes, because the probability of a multiple birth involving a mother who was at least 40 years old is greater than 0.05.
B. Yes, because the probability of a multiple birth involving a mother who was at least 40 years old is less than 0.05. C. No, because the probability of a multiple birth involving a mother who was at least 40 years old is greater than 0.05. D. No, because the probability of a multiple birth involving a mother who was at least 40 years old is less than 0.05.
Answers
Using the given data on the number of live multiple-delivery births for women aged 15 to 54, we need to calculate probabilities related to the age groups of the mothers. The probability of a randomly selected multiple birth involving a mother aged 30 to 39 will be determined, as well as the probabilities of not being in the age range, being less than 45, and being at least 40. Finally, we need to interpret whether a multiple birth involving a mother aged at least 40 is unusual.
(a) To calculate the probability of a randomly selected multiple birth involving a mother aged 30 to 39, we sum the number of multiple births in that age group and divide it by the total number of multiple births for women aged 15 to 54.
P(30 to 39) = 2822 / (89 + 508 + 1631 + 2822 + 1855 + 374 + 119)
(b) To find the probability of a randomly selected multiple birth involving a mother who is not aged 30 to 39, we subtract the probability found in part (a) from 1.
P(not 30 to 39) = 1 - P(30 to 39)
(c) To determine the probability of a randomly selected multiple birth involving a mother aged less than 45, we sum the number of multiple births for age groups below 45 and divide it by the total number of multiple births for women aged 15 to 54.
P(less than 45) = (89 + 508 + 1631 + 2822 + 1855 + 374) / (89 + 508 + 1631 + 2822 + 1855 + 374 + 119)
(d) To find the probability of a randomly selected multiple birth involving a mother aged at least 40, we sum the number of multiple births for age groups 40-44 and 45-54, and divide it by the total number of multiple births for women aged 15 to 54.
P(at least 40) = (374 + 119) / (89 + 508 + 1631 + 2822 + 1855 + 374 + 119)
Interpretation: The answer to part (d) will determine whether a multiple birth involving a mother aged at least 40 is unusual. If the probability is less than 0.05, it can be considered unusual. Therefore, we need to compare the calculated probability to 0.05 and select the correct choice.
To know more about probability here: brainly.com/question/32117953
#SPJ11
what is the fastest thing in the world
Answers
Answer:
The Speed Of Light
Step-by-step explanation:
the sum of the digits of a two-digit number is 8 . when 36 is subtracted from this number, its digits are reversed. find the original number.0
Answers
The original number is 80 and the sum of the digits of a two-digit number is 8 . When 36 is subtracted from this number, its digits are reversed.
Let us suppose that the two-digit number is '10x + y' (as the number is greater than 9 and less than 100, we can represent it as '10x + y' where 'x' is tens digit and 'y' is units digit).
According to the question,
The sum of the digits of a two-digit number is 8
⇒ x + y = 8
Also,
When 36 is subtracted from this number, its digits are reversed
⇒ 10x + y - 36 = 10y + x + 36
⇒ 9x - 9y = 72
⇒ x - y = 8
Therefore, the equations are:
x + y = 8 ........ (1)
x - y = 8 ........ (2)
By adding equations (1) and (2), we get:
2x = 16
⇒ x = 8
By substituting value of 'x' in equation (1), we get:
y = 0
Therefore, the original number is 80.
Conclusion: So, the original number is 80 and the sum of the digits of a two-digit number is 8 . When 36 is subtracted from this number, its digits are reversed.
To know more about number visit
https://brainly.com/question/24627477
#SPJ11
The sum of the digits of a two-digit number is 8 . when 36 is subtracted from this number, its digits are reversed.
The original number is 62.
Let's assume the two-digit number is represented by 10a + b, where a and b are the digits of the number.
According to the given information, we have two conditions:
1. The sum of the digits is 8: a + b = 8.
2. When 36 is subtracted from the number, its digits are reversed: (10a + b) - 36 = 10b + a.
Now we can solve these equations to find the values of a and b.
From equation 1, we have a + b = 8.
From equation 2, we have 10a + b - 36 = 10b + a.
Simplifying equation 2, we get:
9a - 9b = 36.
Dividing both sides by 9, we have:
a - b = 4.
Now we have a system of equations:
a + b = 8,
a - b = 4.
Adding these two equations together, we get:
2a = 12,
a = 6.
Substituting the value of a into one of the equations, we can find b:
6 + b = 8,
b = 2.
Therefore, the original number is 62.
To know more about original number, visit:
https://brainly.com/question/1343101
#SPJ11
URGENT: Figure C and figure E shown on the coordinate plane blow a transformation was performed on figure C to create figure D. Then, a transformation was performed on figure D to create figure E
As a result of the series of transformation performed, figure C is similar figure E, however these figures are not congruent
1• justify why figures C And E are similar and not congruent
2• describe a transformation applied to figure C that will create figure D and then a transformation performed on figure D that will create Figure E

Answers
Answer:
1. Whereby one square = One unit, we have;
Lengths of the sides of figure C are;
4, √(4² + 2²), √(4² + 2²) which simplifies to 4, 2·√5, 2·√5
Lengths of the sides of figure E are;
2, √(1² + 2²), √(1² + 2²) which simplifies to 2, √5, √5
Figure E is equivalent to figure C scaled down by a factor of 1/2
The trigonometric ratios of the two figures are therefore equal and figure C is similar to figure E but figure C is larger than figure E
2. A transformation that will create figure D from figure C is a rotation, 90° counter clockwise about the point (2, -2)
A transformation that will create figure E from figure D is a dilation of figure D by 1/2 with the midpoint of figure D being the center of dilation
Step-by-step explanation:
A quarterback throws an incomplete pass. The height of the football at time t is modeled by the equation h(t) = –16t2 + 40t + 7. Rounded to the nearest tenth, the solutions to the equation when h(t) = 0 feet are –0.2 s and 2.7 s. Which solution can be eliminated and why?
Answers
A quarterback throws an incomplete pass. The height of the football at time t is modeled by the equation h(t) = –16t² + 40t + 7. Rounded to the nearest tenth, the solutions to the equation when h(t) = 0 feet are –0.2 s and 2.7 s.
the solution to be eliminated is -0.2s this is because time do not have negative values
What is a quadratic equation?ax² + bx + c = 0 is a quadratic equation, which is a second-order polynomial equation in a single variable. a.
It has at least one solution because it is a second-order polynomial equation, which is guaranteed by the algebraic fundamental theorem. The answer could be real or complex.
Considering the given function, the answer is both real one is negative the other is positive.
The solution in this case represents time, and time of negative value do not apply in real life
Learn more about quadratic equation at:
https://brainly.com/question/1214333
#SPJ1
question in link below

Answers
Answer:
105
Step-by-step explanation:
2x17=34
17x2.5=42.5
1.5x17=25.5
1/2x2x2x1.5=3
34+42.5+25.5+3=105
Answer Po Ba Ay 11.33?
Step-by-step explanation:
Calc
Can somebody help me with this?

Answers
Answer:
slope = 4/5
Step-by-step explanation:
Take any two points:
(5, 1) & (10, 5)
The slope
\(m=\frac{5-1}{10-5} =\frac{4}{5}\)
Hope this helps
Answer:
4/5 is the slope of the line
What are the steps to solve this

Answers
Malena's steps arranged sequentially are :
collecting like terms Using the appropriate numerical operator divide both sides by 3The first step :
2x + 5 = -10 - x
collecting like terms
2x + x = -10 - 5
step 2 : Using the appropriate numerical operator:
3x = -15
step 3 : divide both sides by 3 to isolate x
x = -5
Hence, the required steps as arranged above .
Learn more on equations :https://brainly.com/question/2972832
#SPJ1
3. Jeff Hittinger is a founder and brewmaster of the Octonia Stone Brew Works in Ruckersville, Virginia. He is contemplating the purchase of a particular type of malt (that is, roasted barley) to use in making certain types of beer. Specifically, he wants to know whether there is a simple linear regression relationship between the mashing temperature (the temperature of the water in which the malted barley is cooked to extract sugar) and the amount of maltose sugar extracted. After conducting 12 trials, he obtains the following data, expressed in terms of (temperature in Fahrenheit, maltose sugar content as a percentage of the total sugar content in the liquid):
(155,25),(160,28),(165,30),(170,31),(175,31),(180,35),(185,33),(190,38),(195,40),
(200,42),(205,43),(210,45)
(a) Calculate the least squares estimators of the slope, the y-intercept, and the variance based upon these data. (b) What is the coefficient of determination for these data? (c) Conduct an upper-sided model utility test for the slope parameter at the 5% significance level. Would you reject the null hypothesis at that significance level?
Answers
a) The least square estimator is 2.785221. b) The coefficient of determination is 0.9960514. c) We would reject the null hypothesis at the 5% significance level.
To calculate the least squares estimators of the slope, the y-intercept, and the variance, we can use the method of simple linear regression.
(a) First, let's calculate the least squares estimators:
Step 1: Calculate the mean of the temperature (x) and maltose sugar content (y):
X = (155 + 160 + 165 + 170 + 175 + 180 + 185 + 190 + 195 + 200 + 205 + 210) / 12 = 185
Y = (25 + 28 + 30 + 31 + 31 + 35 + 33 + 38 + 40 + 42 + 43 + 45) / 12 = 35.333
Step 2: Calculate the deviations from the means:
xi - X and yi - Y for each data point.
Deviation for each temperature (x):
155 - 185 = -30
160 - 185 = -25
165 - 185 = -20
170 - 185 = -15
175 - 185 = -10
180 - 185 = -5
185 - 185 = 0
190 - 185 = 5
195 - 185 = 10
200 - 185 = 15
205 - 185 = 20
210 - 185 = 25
Deviation for each maltose sugar content (y):
25 - 35.333 = -10.333
28 - 35.333 = -7.333
30 - 35.333 = -5.333
31 - 35.333 = -4.333
31 - 35.333 = -4.333
35 - 35.333 = -0.333
33 - 35.333 = -2.333
38 - 35.333 = 2.667
40 - 35.333 = 4.667
42 - 35.333 = 6.667
43 - 35.333 = 7.667
45 - 35.333 = 9.667
Step 3: Calculate the sum of the products of the deviations:
Σ(xi - X)(yi - Y)
(-30)(-10.333) + (-25)(-7.333) + (-20)(-5.333) + (-15)(-4.333) + (-10)(-4.333) + (-5)(-0.333) + (0)(-2.333) + (5)(2.667) + (10)(4.667) + (15)(6.667) + (20)(7.667) + (25)(9.667) = 1433
Step 4: Calculate the sum of the squared deviations:
Σ(xi - X)² and Σ(yi - Y)² for each data point.
Sum of squared deviations for temperature (x):
(-30)² + (-25)² + (-20)² + (-15)² + (-10)² + (-5)² + (0)² + (5)² + (10)² + (15)² + (20)² + (25)² = 15500
Sum of squared deviations for maltose sugar content (y):
(-10.333)² + (-7.333)² + (-5.333)² + (-4.333)² + (-4.333)² + (-0.333)² + (-2.333)² + (2.667)² + (4.667)² + (6.667)² + (7.667)² + (9.667)² = 704.667
Step 5: Calculate the least squares estimators:
Slope (b) = Σ(xi - X)(yi - Y) / Σ(xi - X)² = 1433 / 15500 ≈ 0.0923871
Y-intercept (a) = Y - b * X = 35.333 - 0.0923871 * 185 ≈ 26.282419
Variance (s²) = Σ(yi - y)² / (n - 2) = Σ(yi - a - b * xi)² / (n - 2)
Using the given data, we calculate the predicted maltose sugar content (ŷ) for each data point using the equation y = a + b * xi.
y₁ = 26.282419 + 0.0923871 * 155 ≈ 39.558387
y₂ = 26.282419 + 0.0923871 * 160 ≈ 40.491114
y₃ = 26.282419 + 0.0923871 * 165 ≈ 41.423841
y₄ = 26.282419 + 0.0923871 * 170 ≈ 42.356568
y₅ = 26.282419 + 0.0923871 * 175 ≈ 43.289295
y₆ = 26.282419 + 0.0923871 * 180 ≈ 44.222022
y₇ = 26.282419 + 0.0923871 * 185 ≈ 45.154749
y₈ = 26.282419 + 0.0923871 * 190 ≈ 46.087476
y₉ = 26.282419 + 0.0923871 * 195 ≈ 47.020203
y₁₀ = 26.282419 + 0.0923871 * 200 ≈ 47.95293
y₁₁ = 26.282419 + 0.0923871 * 205 ≈ 48.885657
y₁₂ = 26.282419 + 0.0923871 * 210 ≈ 49.818384
Now we can calculate the variance:
s² = [(-10.333 - 39.558387)² + (-7.333 - 40.491114)² + (-5.333 - 41.423841)² + (-4.333 - 42.356568)² + (-4.333 - 43.289295)² + (-0.333 - 44.222022)² + (-2.333 - 45.154749)² + (2.667 - 46.087476)² + (4.667 - 47.020203)² + (6.667 - 47.95293)² + (7.667 - 48.885657)² + (9.667 - 49.818384)²] / (12 - 2)
s² ≈ 2.785221
(b) The coefficient of determination (R²) is the proportion of the variance in the dependent variable (maltose sugar content) that can be explained by the independent variable (temperature). It is calculated as:
R² = 1 - (Σ(yi - y)² / Σ(yi - Y)²)
Using the calculated values, we can calculate R²:
R² = 1 - (2.785221 / 704.667) ≈ 0.9960514
(c) To conduct an upper-sided model utility test for the slope parameter at the 5% significance level, we need to test the null hypothesis that the slope (b) is equal to zero. The alternative hypothesis is that the slope is greater than zero.
The test statistic follows a t-distribution with n - 2 degrees of freedom. Since we have 12 data points, the degrees of freedom for this test are 12 - 2 = 10.
The upper-sided critical value for a t-distribution with 10 degrees of freedom at the 5% significance level is approximately 1.812.
To calculate the test statistic, we need the standard error of the slope (SEb):
SEb = sqrt(s² / Σ(xi - X)²) = sqrt(2.785221 / 15500) ≈ 0.013621
The test statistic (t) is given by:
t = (b - 0) / SEb = (0.0923871 - 0) / 0.013621 ≈ 6.778
Since the calculated test statistic (t = 6.778) is greater than the upper-sided critical value (1.812), we would reject the null hypothesis at the 5% significance level. This suggests that there is evidence to support a positive linear relationship between mashing temperature and maltose sugar content in this data set.
To learn more about least square estimator here:
https://brainly.com/question/31481254
#SPJ4
Evaluate the indefinite integral. (Use C for the constant of
integration.)
x −
1
x2
x2 +
2
x
2
dx
Answers
he indefinite integral of (x - 1)/(x² + 2x)² dx is (1/8) ln|x + 2| - (1/8) ln|x| - 1/(4(x + 1)²) + C, where C is the constant of integration.
To evaluate the indefinite integral ∫(x - 1)/(x² + 2x² + 2x)² dx, we can proceed with a substitution. Let u = x² + 2x. Then, du = (2x + 2) dx.
Now, let's rewrite the integral in terms of u:
∫(x - 1)/(x² + 2x² + 2x)² dx = ∫(x - 1)/(u²)² * (1/(2x + 2)) du
= ∫(x - 1)/(4u²) * (1/(2x + 2)) du
= ∫(x - 1)/(8u²) * (1/(x + 1)) du
We can simplify the expression further
∫(x - 1)/(8u²) * (1/(x + 1)) du = ∫(x - 1)/(8(x² + 2x)²) du
Now, we can split the integrand into partial fractions
(x - 1)/(8(x² + 2x)²) = A/(x² + 2x) + B/(x² + 2x)²
To find the values of A and B, let's find the common denominator:
A(x² + 2x)² + B(x² + 2x) = x - 1
Expanding and combining like terms:
(A + B) x³ + (4A + 2B) x² + (4A) x + (4A) = x - 1
Matching coefficients, we have the following equations
A + B = 0 (coefficient of x³ terms)
4A + 2B = 0 (coefficient of x² terms)
4A = 1 (coefficient of x terms)
4A = -1 (constant terms)
From the first equation, B = -A.
Substituting this into the second equation: 4A + 2(-A) = 0, we get A = 0.
From the fourth equation: 4A = -1, we find A = -1/4.
Therefore, A = -1/4 and B = 1/4.
Now, we can rewrite the integral with the partial fractions:
∫(x - 1)/(8(x² + 2x)²) du = ∫(-1/4)/(x² + 2x) dx + ∫(1/4)/(x² + 2x)² dx
Let's evaluate each integral separately
∫(-1/4)/(x² + 2x) dx = (-1/4) ∫1/(x(x + 2)) dx
We can apply the method of partial fractions again for this integral. Let's find the values of C and D such that:
1/(x(x + 2)) = C/x + D/(x + 2)
Multiplying both sides by x(x + 2), we get:
1 = C(x + 2) + Dx
Expanding and combining like terms:
1 = (C + D) x + 2C
Matching coefficients, we have:
C + D = 0 (coefficient of x terms)
2C = 1 (constant terms)
From the first equation, D = -C.
Substituting this into the second equation: C - C = 0, we get C = 1/2.
Therefore, C = 1/2 and D = -1/2.
Now, let's rewrite the integral:
∫(-1/4)/(x² + 2x) dx = (-1/4) ∫(1/2x - 1/2(x + 2)) dx
= (-1/8) ln|x| - (-1/8) ln|x + 2| + K1
= (1/8) ln|x + 2| - (1/8) ln|x| + K1
Next, let's evaluate the second integral
∫(1/4)/(x² + 2x)² dx = (1/4) ∫1/(x² + 2x)² dx
We can apply a u-substitution here. Let u = x² + 2x + 1. Then, du = (2x + 2) dx.
Rewriting the integral in terms of u:
(1/4) ∫1/(x² + 2x)² dx = (1/4) ∫1/u² du
= (1/4) (-1/u) + K₂
= -1/(4u) + K₂
Substituting back u = x₂ + 2x + 1:
-1/(4u) + K₂ = -1/(4(x² + 2x + 1)) + K₂
= -1/(4(x + 1)²) + K2
Finally, we can combine the results of both integrals
∫(x - 1)/(8(x² + 2x)²) dx = (1/8) ln|x + 2| - (1/8) ln|x| - 1/(4(x + 1)²) + C
So, the indefinite integral of the given expression is (1/8) ln|x + 2| - (1/8) ln|x| - 1/(4(x + 1)²) + C, where C is the constant of integration.
To know more about integration:
https://brainly.com/question/31954835
#SPJ4
--The given question is incomplete, the complete question is given below " Evaluate the indefinite integral. (Use C for the constant of
integration.) ∫(x - 1)/(x² + 2x² + 2x)²dx "--
much help needed ;;
question attached below

Answers
Answer: f(x)+3
Step-by-step explanation:
g is 3 units ABOVE f. Therefore, f(x)+3 is the only answer, since f(x+3) would only shift the graph to the left, f(x-3) would shift the graph to the right, and f(x)-3 would translate the graph 3 units DOWN, not up. So, the correct answer is f(x) + 3
The quantities x and y are in a proportional relationship.
What do you know about the ratio of y to x for any point (x, y) on the line?
Answers
Answer: constant of proportionality
Explanation: Assuming that we have two proportional quantities; one is x and one is y. If you know whether the relationship between them is direct or inverse proportion, then the ratio of the two quantities y/x gives us a constant generally known as the constant of proportionality.
Write the equation of the line passing through point (-5, -4) and parallel to y = -3

Answers
A line parallel to a horizontal line is also horizontal.
The equation of the line parallel to
\(y=-3\)is of the form
\(y=b\)Since, the line passes through (-5,-4), the value of b is -4
So, the required equation is
\(y=-4\)Hence, the correct option is (c)
Is there a relationship between Column X and Column Y? Perform correlation analysis and summarize your findings.
X Y
10 37
6 10
39 18
24 12
35 11
12 34
33 26
32 9
23 42
10 24
16 40
16 1
35 39
28 24
5 42
22 7
12 17
44 17
15 27
40 47
46 35
35 14
28 38
9 18
9 17
8 22
35 12
15 30
34 18
16 43
19 24
17 45
21 24
Answers
The correlation analysis indicates a moderate positive relationship between Column X and Column Y.
To perform correlation analysis, we can use the Pearson correlation coefficient (r) to measure the linear relationship between two variables, in this case, Column X and Column Y. The value of r ranges from -1 to 1, where 1 indicates a perfect positive correlation, -1 indicates a perfect negative correlation, and 0 indicates no correlation.
Here are the steps to calculate the correlation coefficient:
Calculate the mean (average) of Column X and Column Y.
Mean(X) = (10+6+39+24+35+12+33+32+23+10+16+16+35+28+5+22+12+44+15+40+46+35+28+9+9+8+35+15+34+16+19+17+21) / 32 = 24.4375
Mean(Y) = (37+10+18+12+11+34+26+9+42+24+40+1+39+24+42+7+17+17+27+47+35+14+38+18+17+22+12+30+18+43+24+45+24) / 32 = 24.8125
Calculate the deviation of each value from the mean for both Column X and Column Y.
Deviation(X) = (10-24.4375, 6-24.4375, 39-24.4375, 24-24.4375, ...)
Deviation(Y) = (37-24.8125, 10-24.8125, 18-24.8125, 12-24.8125, ...)
Calculate the product of the deviations for each pair of values.
Product(X, Y) = (Deviation(X1) * Deviation(Y1), Deviation(X2) * Deviation(Y2), ...)
Calculate the sum of the product of deviations.
Sum(Product(X, Y)) = (Product(X1, Y1) + Product(X2, Y2) + ...)
Calculate the standard deviation of Column X and Column Y.
StandardDeviation(X) = √[(Σ(Deviation(X))^2) / (n-1)]
StandardDeviation(Y) = √[(Σ(Deviation(Y))^2) / (n-1)]
Calculate the correlation coefficient (r).
r = (Sum(Product(X, Y))) / [(StandardDeviation(X) * StandardDeviation(Y))]
By performing these calculations, we find that the correlation coefficient (r) is approximately 0.413. Since the value is positive and between 0 and 1, we can conclude that there is a moderate positive relationship between Column X and Column Y.
For more questions like Correlation click the link below:
https://brainly.com/question/30116167
#SPJ11
What is the slope of the line that passes through the points
(
−
9
,
−
7
)
(−9,−7) and
(
−
11
,
−
6
)
(−11,−6)? Write your answer in simplest for
Answers
Considering the expression of a line, the equation of the line that passes through the points (-9,-7) and (-11,-6) is the equation of the line is y= -1/2x -23/2.
Linear equationA linear equation o line can be expressed in the form y = mx + b
where
x and y are coordinates of a point.m is the slope.b is the ordinate to the origin and represents the coordinate of the point where the line crosses the y axis.Knowing two points (x₁, y₁) and (x₂, y₂) of a line, the slope m of a line can be calculated as:
m= (y₂ - y₁)÷ (x₂ -x₁)
Substituting the value of the slope m and the value of one of the points in y=mx +b, the value of the "b" can be obtained.
Equation of the line in this case
Being (x₁, y₁)= (-9, -7) and (x₂, y₂)= (-11, -6), the slope m can be calculated as:
m= (-6 - (-7))÷ (-11 -(-9))
m= (-6 +7)÷ (-11 +9)
m= (1)÷ (-2)
m= -1/2
Considering point 1 and the slope m, you obtain:
-7= (-1/2)×(-9) + b
-7= 9/2 +b
-7 -9/2= b
-23/2= b
Finally, the equation of the line is y= -1/2x -23/2.
Learn more about the equation of a line having 2 points:
brainly.com/question/12851029
brainly.com/question/19496333
#SPJ1
An assembly line has 16 hours to make 1.000 units. What is the required cycle time? (slide 23) 72sec 216sec 57.65sec 14,4sec
Answers
The required cycle-time is approximately 57.6 seconds.
To find the required cycle time, we need to divide the total available time by the number of units to be produced.
Total available time: 16 hours = 16 * 60 minutes = 960 minutes = 960 * 60 seconds = 57,600 seconds
Number of units to be produced: 1,000 units
Required cycle time: Total available time / Number of units
Cycle time = 57,600 seconds / 1,000 units
Cycle time ≈ 57.6 seconds
Therefore, the required cycle time is approximately 57.6 seconds.
Learn more about cycle-time from the given link
https://brainly.com/question/15356513
#SPJ11
factor the algebric expression 32a+36
Answers
Answer:
a = 1.125
is your compleate full answer
Answer:
the factorised form is 4(8a+9)
Y=-3x-1 find the solution
Answers
The equation Y=-3x-1 represents a linear relationship between x and y, and can be used to model real-world situations such as distance vs. time or cost vs. quantity.
The equation Y=-3x-1 represents a straight line on a coordinate plane. The "slope-intercept" form of the equation is y=mx+b, where m is the slope and b is the y-intercept.
In this case, the slope is -3 and the y-intercept is -1. This means that the line goes downwards at a rate of 3 units for every 1 unit to the right, and intersects the y-axis at -1.
To find the solution to this equation, you would need to have a specific value for either x or y.
If you were given a value for x, you could plug it into the equation to find the corresponding value for y. If you were given a value for y, you could solve for x by rearranging the equation.
To learn more about : equation
https://brainly.com/question/17145398
#SPJ11
A single number that estimates the value of an unknown parameter is called a _______ estimate.
Answers
Answer:
A single number that estimates the value of an unknown parameter is called a point estimate.
Step-by-step explanation:
Don't see the point (haha) of elaborating
Help please. will give brainliest.

Answers
Answer:
I guess the two angles have to be equal to 180°, so: 15x+48+5x+12=180
solve it:
20x+60=180
20x=180-60
20x=120
x=6 is the correct answer.
C = (2^40 + 2^39 + 2^38):7

Answers
Answer:
\(\red{ \bf \: c = {2}^{38} \: }\)
Step-by-step explanation:
\( \bf c = ( {2}^{40}+{2}^{39}+{2}^{38}):7 \)
\(\bf c = {2}^{38} \cdot( {2}^{40 - 38}+{2}^{39 - 38}+{2}^{38 - 38}):7 \)
\(\bf c = {2}^{38} \cdot( {2}^{2}+{2}^{1}+{2}^{0}):7 \)
\(\bf c = {2}^{38} \cdot( 4+2+1):7 \)
\(\bf c = {2}^{38} \cdot7:7 \)
\( \red{ \boxed{\bf \: c = {2}^{38} \: }}\)
A flight attendant was counting the number of passengers present to see if any upgrades could be offered. The flight attendant's list contained passengers' Frequent Flyer status as well as number of bags checked. 0 checked bags 1 checked bag Bronze status 5 3 Silver status 6 6 What is the probability that a randomly selected passenger has bronze status and 1 checked bag? Simplify any fractions.
Answers
Answer:
7
Step-by-step explanation:
Write an equation for the line that is parallel to the given line and passes through the given point . Write the equation of the line in y=mx+b form
y=5x-7;(2,-2)
Answers
A parallel line has the same slope as the original equation. Therefore, the slope (m in y=mx+b) will be 5. From there, we can use the point-slope formula and convert it into the slope-intercept formula (y=mx+b).
Point-slope is:
y-y₁=m(x-x₁)
Plug in our known values:
y-(-2)=5(x-(2))
Distribute and set it equal to y:
y+2=5x-10
y=5x-12
Let me know if you have any more questions :)
The exact value of Tan 30 x sin 60
Answers
Answer:
\(\frac{1}{2}\)
Step-by-step explanation:
\(\tan \left(30^{\circ \:}\right)=\frac{\sqrt{3}}{3}\)
\(\quad \sin \left(60^{\circ \:}\right)=\frac{\sqrt{3}}{2}\)
\(=\frac{\sqrt{3}}{3}\times \frac{\sqrt{3}}{2}\)
\(=\frac{3}{6}\)
\(=\frac{1}{2}\)
Answer:
\(1/2\)
Step-by-step explanation:
Tan 30 = \(\frac{\sqrt{3} }{3}\)
Sin 60 = \(\frac{\sqrt{3} }{2}\)
Multiply the 2 roots you get my answer 1/2
PLS HeLp ASAP I nEEd HELp
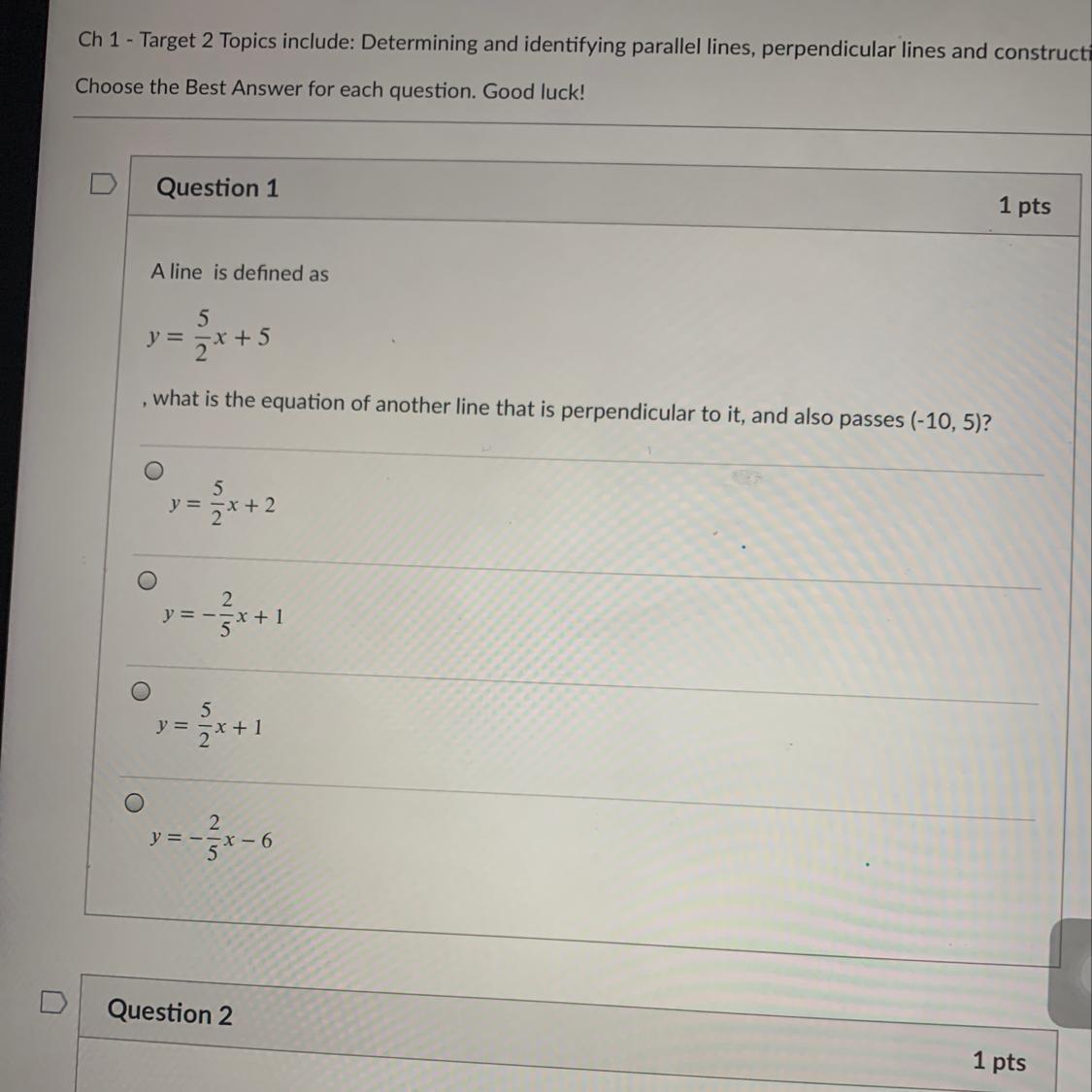
Answers
Answer:
the last bubble
Step-by-step explanation:
Perpendicular lines have opposite reciprocal slopes
the original line: y = 5/2x + 5
The perpendicular line: y = -2/5x + b
To find b, we have to plug (-10, 5) into x and y for our perpendicular line
5 = -2/5(-10) + b
Simplify the right side
5 = 4 + b
Subtract 4 from both sides
1 = b
The final answer = y = -2/5x + 1
ok so hi I need help with this

Answers
Answer:
x=-5, 5
Step-by-step explanation:
Because there is absolute value symbol and is equal to 5.
PLEASE HELP ME PLEASE
Solve the equation
2/3x - 2 = 7
13 1/2
-13 1/2
15 1/2
6

Answers
(2/3)x = 7 + 2
(2/3)x = 9
2x = 9 × 3
x = 27/2
:. x = 13 1/2
The following is a set of data from a sample of n=7 1211162015168 p (a) Compute the first quartile (Q 1
), the third quartile (Q 3
), and the interquartile range (b) List the five-number summary. (c) Construct a boxplot and describe the shape: (a) The first quartile is
Answers
Q1 = 15, Q3 = 20, Interquartile range = 5.
To compute the first quartile (Q1), third quartile (Q3), and interquartile range, we first need to arrange the data in ascending order: 8, 11, 12, 15, 16, 20, 21.
Q1 represents the value below which 25% of the data falls. In this case, Q1 is the median of the lower half of the data set.
Since we have an odd number of data points, Q1 is the middle value of the lower half: Q1 = 15.
Q3 represents the value below which 75% of the data falls. It is the median of the upper half of the data set.
Again, since we have an odd number of data points, Q3 is the middle value of the upper half: Q3 = 20.
The interquartile range is the difference between Q3 and Q1: Interquartile range = Q3 - Q1 = 20 - 15 = 5.
The five-number summary includes the minimum value, Q1, median, Q3, and maximum value. In this case, the five-number summary is: 8, 15, 16, 20, 21.
To construct a boxplot, we plot a number line and mark the five-number summary.
The boxplot consists of a box spanning from Q1 to Q3, with a line inside representing the median.
The minimum and maximum values are marked with whiskers extending from the box. In this case, the boxplot would have a box from 15 to 20, with the median line at 16.
The whiskers would extend to 8 as the minimum value and 21 as the maximum value.
Based on the given data, we can describe the shape of the boxplot. However, without knowing the actual data values, it is difficult to determine the exact shape.
The boxplot provides a visual representation of the distribution, showing the spread, skewness, and outliers, if any.
Learn more about the Interquartile range:
brainly.com/question/29173399
#SPJ11
1.70p−0.34q 0.17(q 1)−0.85(p−1) =0 =0 consider the system of equations above. how many (p, q)(p,q)left parenthesis, p, comma, q, right parenthesis solutions does this system have?
Answers
The system has exactly one solution, which is (p, q) = (-0.2118, -8.0).
We are given the system of equations:
1.7p - 0.34q = 0
0.17(q+1) - 0.85(p-1) = 0
We can simplify the second equation by distributing the 0.17 and 0.85 terms:
0.17q + 0.17 - 0.85p + 0.85 = 0
0.17q - 0.85p = -0.72
Now we have two equations in two variables, which we can solve using substitution or elimination. We will use elimination here.
Multiplying the first equation by 5, we get:
8.5p - 1.7q = 0
Multiplying the second equation by 2, we get:
0.34q - 1.7p = -1.44
Adding these two equations, we get:
6.8p = -1.44
p = -0.2118
Substituting this value of p into either of the original equations, we get:
1.7(-0.2118) - 0.34q = 0
q = -8.0
So the system has exactly one solution, which is (p, q) = (-0.2118, -8.0).
Learn more about solution here
https://brainly.com/question/24644930
#SPJ11
