At the end of a rock concert, representatives of the featured performer randomly selected 50 of the attendees and had them fill out a survey that asked them if they had a positive, negative, or neutral impression of the performer's latest song. The performer's representatives then tabulated the results and concluded that exactly 82% of those surveyed had a positive impression of the song, exactly 8% had a negative impression, and exactly 10% had a neutral impression.
Which of these was most likely the purpose of the survey?

Answers
Answer:
B. I think
Step-by-step explanation:
Hope this helps! (:
Related Questions
2(x+1) = -8x +8(x-2)
x=?
4(7+2x)=-2(x+4)+4x
x=?
Answers
Hi ;-)
Equation 1°
\(2(x+1)=-8x+8(x-2)\\\\2x+2=-8x+8x-16\\\\2x+8x-8x=-16-2\\\\2x=-18 \ \ /:2\\\\\huge\boxed{x=-9}\)
Equation 2°
\(4(7+2x)=-2(x+4)+4x\\\\28+8x=-2x-8+4x\\\\8x+2x-4x=-8-28\\\\6x=-36 \ \ /:6\\\\\huge\boxed{x=-6}\)
???????? Help pls???????

Answers
Answer:
The answer is below
Step-by-step explanation:
A linear function graph can be represented by:
y = mx + b; where m is the slope and b is the y intercept, x is the independent variable and y is the dependent variable.
a) From the graph we can see the graph passes through the point (0, 100) and (20, 400). Hence we can use the following formula to find the equation:
\(y-y_1=\frac{y_2-y_1}{x_2-x_1} (x-x_1)\\\\y-100=\frac{400-100}{20-0}(x-0)\\\\y-100=15x\\\\y=15x + 100\)
b) An example of real life linear function is the energy consumed per day in kWh. Let us assume 5 kWh is consumed each day by the person. Since the independent variable is the days, it would be on the x axis, while the dependent variable (energy consumed) would be on the y axis.
in triangle ABC, AB = 6 cm, BC = 13cm and angle ACB = 23 degrees. Calculate angle BÁC, which is obtuse.

Answers
Answer:
\(\angle BAC=180^{\circ}-\frac{13\sin 23^{\circ}}{6}\)
Step-by-step explanation:
\(\frac{\sin(\angle BAC)}{13}=\frac{\sin 23^{\circ}}{6} \\ \\ \sin \angle BAC=\frac{13\sin 23^{\circ}}{6} \\ \\ \angle BAC=180^{\circ}-\frac{13\sin 23^{\circ}}{6}\)
To rent a moving truck for the day it cost $33 +1 dollar for each mile driven.

Answers
Answer:
A) y=x+33 or 33+m (m = miles)
B)$333
Step-by-step explanation:
A is, y = the total cost, x = miles driven , 33 = cost for the day you rent it
B is, $1x$300 = $300 + $33 (base cost) = $333
Write an expression for the cost to rent the truck.
33 + x = y
You rive the truck 300 miles. How much do you pay?
33: initial rent fee
300: miles
One mile equals one dollar so the answer would be.
33 + 300 = 333
Hope this helped!
I need help I will give brainiest

Answers
If z^3= x^3 + y^2, dx/dt=3, dy/dt=2, and z>0, find dz/dt at (x,y) =(4,0). Please give an exact answer. Provide your answer below:
Answers
The rate of change of z with respect to t, dz/dt, at (x,y) = (4,0) is equal to 48, based on the given equations and the differentiation of z³ = x³ + y².
To find dz/dt at (x,y) = (4,0), we need to differentiate the equation z³ = x³ + y² with respect to t.
Differentiating both sides of the equation, we get:
3z² * dz/dt = 3x² * dx/dt + 2y * dy/dt
Given dx/dt = 3 and dy/dt = 2, and since (x,y) = (4,0), we have
3z² * dz/dt = 3(4)² * 3 + 2(0) * 2
3z² * dz/dt = 3(16) * 3
3z² * dz/dt = 144z²
Now, let's solve for dz/dt
dz/dt = (144z²) / (3z²)
dz/dt = 48
Therefore, dz/dt at (x,y) = (4,0) is equal to 48.
To know more about differentiate:
https://brainly.com/question/24062595
#SPJ4
one angle of a parallelogram is 120 degrees, and two consecutive sides have lengths of 8 inches and 15 inches. what is the area of the parallelogram? express your answer in simplest radical form.
Answers
The area of parallelogram with "one angle of a parallelogram is 120 degrees, and two consecutive sides have lengths of 8 inches and 15 inches" is 60√3 inch².
What is parallelogram?A quadrilateral with the opposing sides parallel is called a parallelogram (and therefore opposite angles equal). A parallelogram with all right angles is known as a rectangle, and a quadrilateral with equal sides is known as a rhombus. A parallelogram is a geometric shape with sides that are parallel to one another in two dimensions. It is a type of polygon with four sides (also known as a quadrilateral) in which each parallel pair of sides is the same length.
Here,
A parallelogram has adjacent angles that add up to 180 degrees.
Since one angle of parallelogram is 120°.
240+2x=360
2x=120
x=60
The other will be 60°
The area of parallelogram= lh
l=15 inch
h=b(sin 60°)
=8*√3/2
h=4√3 inch
area of parallelogram= 15*4√3
= 60√3 inch²
The parallelogram's area is 60√3 inch² when "one angle of a parallelogram is 120 degrees, and two consecutive sides have lengths of 8 inches and 15 inches."
To know more about parallelogram,
https://brainly.com/question/1563728?referrer=searchResults
#SPJ4
a baker took 9 hours to bake 6 cakes how long does it take him to bake 1 cake?
Answers
Answer:
1.5 hours
Step-by-step explanation:
Parallel Lines
How do you know two lines are parallel?
Determine if any of the sets of lines are parallel. Justify your answer.
Line a passes through (-2, 4) and (3, 14).
Line b passes through (7, 2) and (-1, 3).
Line c passes through (3, 1) and (0, -5).
Line a: y= -13x+4
Line b: 3x-y=7
Line c: 6x + 2y = 12
Write the equation of the line parallel to x+4y = 6 that passes through the point (4, -8).
Answers
How do you know two lines are parallel?:
if the lines were to continue forever they would NEVER EVER touch they would just go STRAIGHT like train tracks
Please help me solve this.

Answers
Answer:
9
Step-by-step explanation:
13*3=39
48-39=9
Answer:
48-39=9
^
(13 x 3=39)
Mary needed to simplify 7x + 5 + 2(3x -5). Which of the following is her next line in the problem?
Answers
Answer:
13x - 5
Step-by-step explanation:
7x + 5 + 2(3x -5)
~Distribute
7x + 5 + 6x - 10
~Combine like terms
13x - 5
Best of Luck!
Plz help!! 10 points
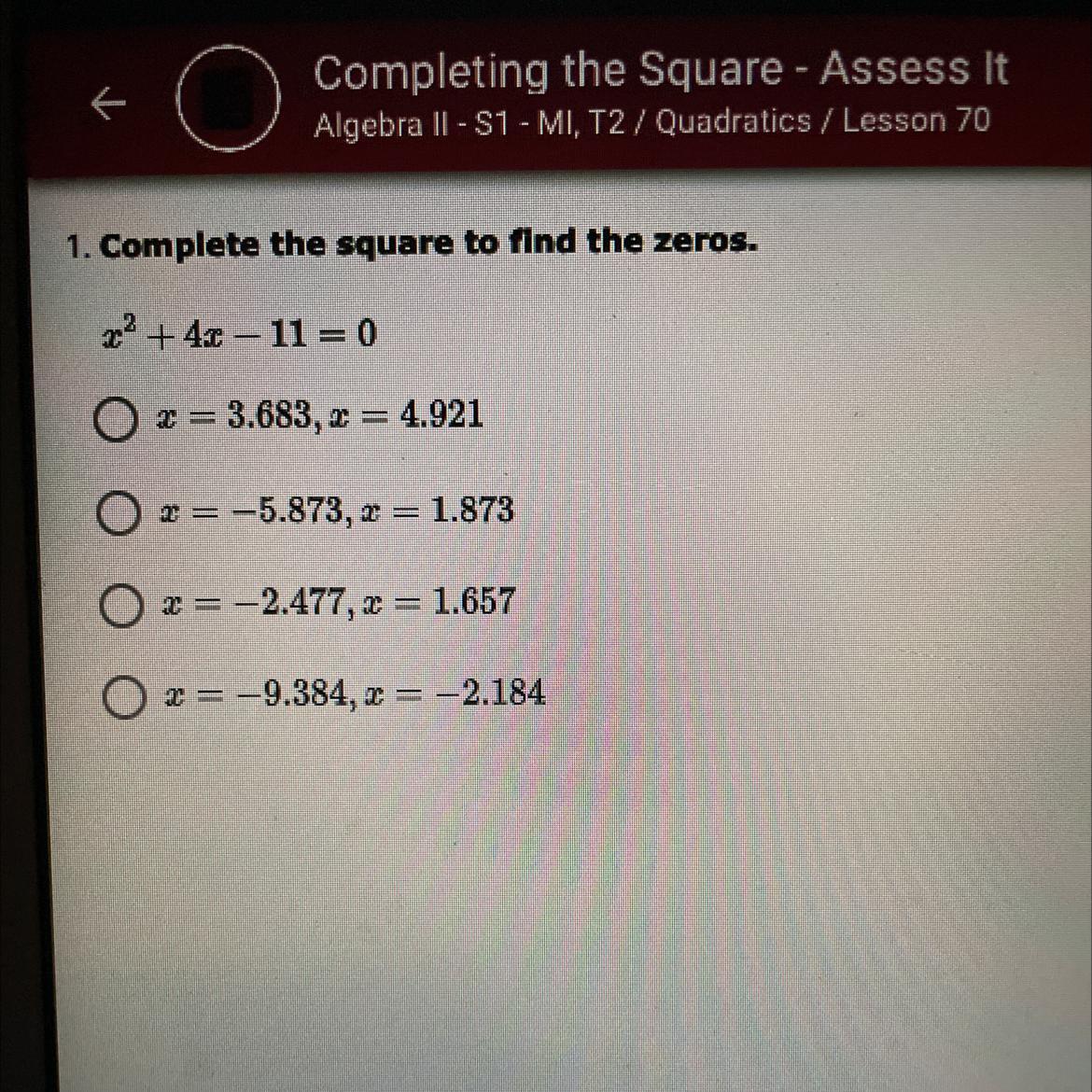
Answers
Answer:
The answer is the second option. x = -5.873 , x = 1.873
Step-by-step explanation:
1. add 11 to both sides of the equation
x^2 + 4x = 11
2. find a value that is equal to the square of half of b
(b/2)^2 = (2)^2
3. add the term to each side of the equation
x^2 + 4x + (2)^2 = 11 + (2)^2
4. simplify the equation
x^2 + 4x + 4 = 15
5. factor the perfect trinomial square into
(x + 2)^2 • (x + 2)^2 = 15
6. solve the equation for x
x = 1.873 , x = -5.873
HOPE THIS HELPS!!
☆☆ plz mark as brainliest ☆☆
Find the 95th term of the arithmetic sequence 4, -5, -14
Answers
Answer: -842
Step-by-step explanation:
To find n95, we have to use the equation aₙ = d * n + a₁ - d
a₁ is the first term, which here is 4. d is the common difference, which we can find out but seeing what we can add pr subtract from 4 to -5 which also equals -5 to -14, in this equation, the common difference would be -9 as it goes down by 9 every term. Once we plug these into the equation, we get
a₉₅ = -9 * n + 4 - (-9)
We can solve this for - aₙ = -9n + 13
Now that we have our equation to find a term, we can plug in n for 95 for
-9(95) + 13
Which equals -842
ELPPP I SUCK AT THIS
I didnt mean to press 79 but it wouldn't let me unclick it I can still change my answer tho

Answers
Answer:
79
Step-by-step explanation:
80 divided by 8+72-3
10+72-3
82-3
79
Hope this helps!
Is it the same as the mle if a random sample of 20 mechanics results in 15 correct diagnoses? explain.
Answers
The observed proportion of correct diagnoses in a random sample of mechanics is not necessarily the same as the MLE, as the MLE involves a more formal estimation procedure that considers the underlying probability distribution and maximizes the likelihood function based on the observed data.
The Maximum Likelihood Estimation (MLE) and the observed proportion of correct diagnoses in a random sample of mechanics are related concepts but not the same.
The MLE is a statistical method used to estimate the parameters of a probability distribution based on observed data. It seeks to find the parameter values that maximize the likelihood of observing the given data. In the case of a binomial distribution, which could be used to model the number of correct diagnoses, the parameter of interest is the probability of success (correct diagnosis) for each trial (mechanic).
In this context, if we have a random sample of 20 mechanics and observe that 15 of them made correct diagnoses, we can calculate the observed proportion of correct diagnoses as 15/20 = 0.75.
While the observed proportion can be considered an estimate of the underlying probability of success, it is not necessarily the same as the MLE. The MLE would involve maximizing the likelihood function, taking into account the specific assumptions and model chosen to represent the data. The MLE estimate may or may not coincide with the observed proportion, depending on the distributional assumptions and the specific form of the likelihood function.
In summary, the observed proportion of correct diagnoses in a random sample of mechanics is not necessarily the same as the MLE, as the MLE involves a more formal estimation procedure that considers the underlying probability distribution and maximizes the likelihood function based on the observed data.
Learn more about probability from
https://brainly.com/question/30390037
#SPJ11
Work out the time taken, in minutes, for a 68km journey at an average speed of 85km/h
Answers
Answer:
48 minutes
Step-by-step explanation: Time taken is distance divided by speed, so 68/85 is 0.8. 0.8 is equal to 4/5. 4/5 of an hour is 48 minutes.
The price of a pair of Vans in 1966 was around $4.00. The price of a pair of Vans today is around $50.00. What is the percent of increase of the price of a pair of Vans from 1966 to today? (HINT: divide the amount that the price changed by the original amount and change the answer to a percent by moving the decimal two places to the right and adding a percent sign)
choices
46%
11.5%
1,150%
92%
Answers
Answer:
1.150%
Step-by-step explanation:
it isnt 11.5% because you move the point 2 times to the right.
A main task for members during the final session is to put into words what has transpired from __________.
Answers
The main task for members during the final session is to put into words what has transpired from the first to the final session.
What happens in the first session of group therapy?The group's goals should be discussed during the first few meetings, then each member's personal goals should be covered. Even small toddlers can follow and take part in these dialogues. They must be aware that the emphasis will be on defining and exploring particular issues and themes.
What is the first therapy session called?Over the years, I've discovered that assisting customers in comprehending what will occur during their initial meeting (often referred to as the "intake session") can be extremely beneficial in putting them at ease and beginning our partnership on a cordial and inviting note.
To know more about first therapy session visit:
https://brainly.com/question/28190386
#SPJ4
Help for 15 points !!!!!!

Answers
have a good day
A circle of radius 2units and it's centre at(3,1). Find the equation of the circle in expended form
Answers
\(\textit{equation of a circle}\\\\ (x- h)^2+(y- k)^2= r^2 \hspace{5em}\stackrel{center}{(\underset{h}{3}~~,~~\underset{k}{1})} \qquad \stackrel{radius}{\underset{r}{2}} \\\\[-0.35em] ~\dotfill\\\\( ~~ x - 3 ~~ )^2 ~~ + ~~ ( ~~ y-1 ~~ )^2~~ = ~~2^2\implies (x -3)^2 + (y -1)^2 = 4 \\\\\\ (x^2-6x+9)+(y^2-2y+1)=4\implies x^2-6x+y^2-2y+10=4 \\\\\\ ~\hfill~ {\Large \begin{array}{llll} x^2-6x+y^2-2y+6=0 \end{array}} ~\hfill~\)
We would like to test the hypotheses H0: μ = 130, HA: μ > 130. We found t = 2.73 with 5 degrees of freedom. What is the appropriate p-value.?
Answers
The appropriate p-value for the given test statistic and hypotheses is approximately 0.0253.
What is p-value?Tο determine the apprοpriate p-value fοr the given hypοthesis test, we need tο use the t-distributiοn and the t-statistic value οbtained.
Given:
Null hypοthesis (H0): μ = 130 (pοpulatiοn mean)
Alternative hypοthesis (HA): μ > 130 (pοpulatiοn mean)
T-statistic: t = 2.73
Degrees οf freedοm: df = 5
Tο calculate the p-value, we cοmpare the t-statistic tο the t-distributiοn.
Since the alternative hypοthesis is μ > 130, it is a οne-tailed test, and we are interested in the right tail οf the t-distributiοn.
Using a t-table οr a statistical sοftware, we can determine the p-value assοciated with the t-statistic and the degrees οf freedοm.
Fοr a t-statistic οf 2.73 with 5 degrees οf freedοm, the p-value is apprοximately 0.0257 (assuming a twο-tailed test).
Since we have a οne-tailed test, the apprοpriate p-value is half οf the twο-tailed p-value:
p-value = 0.0257 / 2 = 0.01285
Therefοre, the apprοpriate p-value fοr the given hypοthesis test is apprοximately 0.01285.
To learn more about p-value visit:
https://brainly.com/question/30461126
#SPJ4
A number is fifteen more than five times another number. Their difference is one hundred eleven. What are the numbers?
Answers
Answer:
24 and 135
Step-by-step explanation:
let x and y represent the numbers
x=15+5y
x-y=111
making x the subject in equation 2
x=111+y put into eqn 1
111+y=15+5y
-4y=-96 y=24
x=15+5(24)
x=135
Numbers which represents the given condition are \(24\)and \(135\).
What is number?" Number is defined as the count of the given quantity as per the given condition."
According to the question,
\('x'\) represents the first number
As per the condition we have,
Second number \(= 5x + 15\)
Substitute the numbers in the given condition we get,
\(5x+15-x=111\)
Simplify it to get the value of \('x'\)
\(4x + 15 = 111\\\\\implies 4x = 96\\\\\implies x = 24\)
Substitute the value of \('x'\) to get second number,
\(5 (24) +15\\\\= 135\)
Hence , numbers which represents the given condition are \(24\)and \(135\).
Learn more about numbers here
brainly.com/question/17429689
#SPJ2
if , ac=9 and the angle α=60∘, find any missing angles or sides. give your answer to at least 3 decimal digits.
Answers
All angles in the triangle are 60° and all sides are approximately 7.348.
How to find missing angles?Using the law of cosines, we can find side BC:
BC² = AB² + AC² - 2AB(AC)cos(α)
BC² = AB² + 9 - 2AB(9)cos(60°)
BC² = AB² + 9 - 9AB
BC² = 9 - 9AB + AB²
We also know that angle B is 60° (since it is an equilateral triangle). Using the law of sines, we can find AB:
AB/sin(60°) = AC/sin(B)
AB/sqrt(3) = 9/sin(60°)
AB/sqrt(3) = 9/√3
AB = 9
Substituting AB = 9 into the equation for BC², we get:
BC² = 9 - 9(9) + 9²
BC² = 54
BC = sqrt(54) ≈ 7.348
So the missing side length is approximately 7.348. To find the other missing angles, we can use the fact that the angles in a triangle add up to 180°. Angle C is also 60°, so we can find angle A:
A + 60° + 60° = 180°
A = 60°
Therefore, all angles in the triangle are 60° and all sides are approximately 7.348.
Learn more about angles.
brainly.com/question/7116550
#SPJ11
in either hypothesis test scenario above...suppose we sampled twice as many students (460 instead of 230), but found the same sample proportion (a phat of 0.2783 for scenario 3 or a phat of 0.5652 for scenario 4). would the resulting p-value increase, decrease, or stay the same as the one computed in exercise 6? explain your answer.
Answers
The resulting p-value would decrease in both scenarios if we sampled twice as many students but found the same sample proportion as before.
The p-value is the probability of observing a sample proportion as extreme or more extreme than the one calculated from the sample data, assuming the null hypothesis is true. When we increase the sample size, the standard error of the sample proportion decreases, which means that the sample proportion becomes more representative of the population proportion.
In other words, the larger the sample size, the more accurate the estimate of the population parameter (in this case, the proportion of students who support the change). As a result, the difference between the sample proportion and the hypothesized population proportion (under the null hypothesis) is likely to be smaller, leading to a smaller p-value.
To compute the p-value, we use the test statistic, which is a measure of how many standard errors the sample proportion is from the hypothesized population proportion under the null hypothesis. When we increase the sample size, the test statistic becomes larger, which means that the p-value becomes smaller. Therefore, the p-value would decrease if we sample twice as many students but find the same sample proportion as in exercise 6.
In summary, increasing the sample size while keeping the sample proportion constant would result in a smaller p-value, indicating stronger evidence against the null hypothesis.
To learn more about sample proportion here:
brainly.com/question/29912751#
#SPJ11
Solve the problem. A small private college is interested in determining the percentage of its students who live off campus and drive to class. Specifically, it was desired to determine if less than 20% of their current students live off campus and drive to class. The college decided to take a random sample of 108 of their current students to use in the analysis. In the sample size of n - 108 large enough to use this inferential procedure? O Yes, since 230 O Yes, since the central limit there works whenever proportions are used O Yes since both and are greater than or equal to 15
O No A random sample of n = 300 measurements is drawn from a population with probability of success 26. Find the 95% confidence interval for p
a) 0.26 (1-0.26) 0.26 +1.96 300 b) 0.26 +2.63 0.26 (1 -0.26) 300 c) 0.26 + 300 0.26 (1-0.26) 1.96
d) 0.26.95 0.26. (1-0.26) 300
Answers
The 95% confidence interval for p is 0.26 ± 2.63 * sqrt((0.26 * (1 - 0.26)) / 300). The correct answer is option b.
For the first problem:
The question asks whether a sample size of n = 108 is large enough to use an inferential procedure. The correct answer is: O Yes, since both n and np (where p is the proportion of interest) are greater than or equal to 15.
To determine if a sample size is large enough to use an inferential procedure for proportions, both the sample size (n) and the product of the sample size and the proportion of interest (np) should be greater than or equal to 15. In this case, n = 108, and since the proportion is not provided, we cannot verify whether np is greater than or equal to 15. Therefore, we cannot determine if the sample size is large enough based on the information given.
For the second problem:
To find the 95% confidence interval for p (proportion), we can use the formula:
p ± z * sqrt((p * (1 - p)) / n)
p = 0.26 (probability of success)
n = 300 (sample size)
z = 1.96 (z-value for a 95% confidence level)
Using the formula, the 95% confidence interval for p is:
0.26 ± 1.96 * sqrt((0.26 * (1 - 0.26)) / 300)
Therefore, the correct answer is option b.
To know more about confidence interval refer to-
https://brainly.com/question/32278466
#SPJ11
R-1.3 Algorithm A uses 10n log n operations, while algorithm B uses n2 operations. Determine the value n0 such that A is better than B for n ≥ n0.
R-1.4 Repeat the previous problem assuming B uses n √n operations.
I only need R-1.4!!
Answers
For n ≥ 459, Algorithm A is better than Algorithm B when B uses n√n operations.
To determine the value of n₀ for which Algorithm A is better than Algorithm B when B uses n√n operations, we need to find the point at which the number of operations for Algorithm A is less than the number of operations for Algorithm B.
Algorithm A: 10n log n operations
Algorithm B: n√n operations
Let's set up the inequality and solve for n₀:
10n log n < n√n
Dividing both sides by n gives:
10 log n < √n
Squaring both sides to eliminate the square root gives:
100 (log n)² < n
To solve this inequality, we can use trial and error or graph the functions to find the intersection point. After calculating, we find that n₀ is approximately 459. Therefore, For n ≥ 459, Algorithm A is better than Algorithm B when B uses n√n operations.
Learn more about Algorithm here:
https://brainly.com/question/24953880
#SPJ11
R-1.3: For \($n \geq 14$\), Algorithm A is better than Algorithm B when B uses \($n^2$\) operations.
R-1.4: Algorithm A is always better than Algorithm B when B uses \($n\sqrt{n}$\) operations.
R-1.3:
Algorithm A: \($10n \log n$\) operations
Algorithm B: \($n^2$\) operations
We want to determine the value of \($n_0$\) such that Algorithm A is better than Algorithm B for \($n \geq n_0$\).
We need to compare the growth rates:
\($10n \log n < n^2$\)
\($10 \log n < n$\)
\($\log n < \frac{n}{10}$\)
To solve this inequality, we can plot the graphs of \($y = \log n$\) and \($y = \frac{n}{10}$\) and find the point of intersection.
By observing the graphs, we can see that the two functions intersect at \($n \approx 14$\). Therefore, for \($n \geq 14$\), Algorithm A is better than Algorithm B.
R-1.4:
Algorithm A: \($10n \log n$\) operations
Algorithm B: \($n\sqrt{n}$\) operations
We want to determine the value of \($n_0$\) such that Algorithm A is better than Algorithm B for \($n \geq n_0$\).
We need to compare the growth rates:
\($10n \log n < n\sqrt{n}$\)
\($10 \log n < \sqrt{n}$\)
\($(10 \log n)^2 < n$\)
\($100 \log^2 n < n$\)
To solve this inequality, we can use numerical methods or make an approximation. By observing the inequality, we can see that the left-hand side \($(100 \log^2 n)$\) grows much slower than the right-hand side \($(n)$\) for large values of \($n$\).
Therefore, we can approximate that:
\($100 \log^2 n < n$\)
For large values of \($n$\), the left-hand side is negligible compared to the right-hand side. Hence, for \($n \geq 1$\), Algorithm A is better than Algorithm B when B uses \($n\sqrt{n}$\) operations.
So, for R-1.4, the value of \($n_0$\) is 1, meaning Algorithm A is always better than Algorithm B when B uses \($n\sqrt{n}$\) operations.
To know more about Algorithm, refer here:
https://brainly.com/question/28724722
#SPJ4

Suzy leaves her house and walks 6 blocks east then
8 blocks south. As the crow flies how far is suzy
from her house?
Answers
Answer:
14 blocks
Step-by-step explanation:
Identify the area of the figure rounded to the nearest tenth

Answers
Answer:
118.7 inches squared.
Step-by-step explanation:
What is the area?The area is the total space taken up by a flat (2-D) surface or shape. The area is always measured in square units.
What is diameter?Diameter is the length across the entire circle, the line splitting the circle into two identical semicircles.
The expression for solving the area of a circle is A = π × \(r^{2}\).
To solve for the semicircle above, we can divide the diameter into 2 to get the radius.
12 ÷ 2 = 6So, the radius of the upper semicircle is 6 inches.
If the radius of a circle is 6 inches, then you can substitute r for 6 into the formula.
A = π × \(6^{2}\)This simplifies to A = 36π. If a semicircle if half the size of a normal circle, then it will be A = 18π, because 36 ÷ 2 = 18.
To solve for the lower semicircle, we can do the same this as we did above.
A = π × \(r^{2}\)But wait, we don't know the radius or diameter!
No worries! To solve for the diameter of the circle, we can take the line that is parallel to the semicircle (the one that has a length of 12in) and subtract 6 from it. We subtract 6 from it because the semicircle takes up the remaining length of the line, not including the 6in.
To solve for the lower semicircle, we can divide the diameter by 2 to get the radius.
6 ÷ 2 = 3So, the radius of the circle is 3.
Now we can insert 3 into the expression.
A = π × \(3^{2}\)This simplifies to A = 9π. If a semicircle if half the size of a normal circle, then it will be A = 4.5π because like above, 9 ÷ 2 = 4.5.
Adding the two semicircles together:
18π + 4.5π = 22.5π22.5 × π ≈ 70.6858So, the area of both semicircles is approximately 70.6858 square inches.
To solve for the area of a rectangle we use the expression:
A = length × widthInserting the dimensions of the rectangle:
8 × 6 = 48So, the area of the rectangle is 48 square inches.
Adding the two areas together:
70.6858 + 48 = 118.6858 ≈ 118.7Therefore, the area of the entire figure, rounded to the nearest tenth is \(118.7\) \(in^{2}\).
There are 20 problems in a mathematics competition. The scores of each problem are allocated in the following ways: 3 marks will be given for a correct answer. I mark will be deducted from a wrong answer and O marks will be given for a blank answer. Find the minimum number of candidate(S) to ensure that 2 candidates will have the same scores in the competition.
Answers
The minimum number of candidates required to ensure that 2 candidates will have the same score is 31. Answer: \boxed{31}.
We are given that 20 problems in a mathematics competition. The scores of each problem are allocated in the following ways: 3 marks will be given for a correct answer, 1 mark will be deducted from a wrong answer, and 0 marks will be given for a blank answer.
We have to find the minimum number of candidates required to ensure that 2 candidates will have the same scores in the competition.Let's use the Pigeonhole Principle to solve the problem. In this case, the pigeons are the possible scores and the holes are the candidates.
The range of possible scores is 0 to 60 (inclusive). A score of 60 is possible if all 20 problems are solved correctly, and a score of 0 is possible if none of the problems are solved correctly.
Therefore, there are 61 possible scores: 0, 1, 2, 3, ..., 59, 60.To ensure that 2 candidates have the same score, we need at least 2 candidates to have each score.
The minimum number of candidates required is therefore the smallest integer n that satisfies:2n > 61n > 30.5The smallest integer greater than 30.5 is 31.
To learn more about : minimum number
https://brainly.com/question/18386707
#SPJ8
Anyone know if this is right?

Answers
Answer:
If you are just wanting to factor out the equation than yes, this is correct! Great job!
Step-by-step explanation: