assume that all the given functions have continuous second-order partial derivatives. if z = f(x, y), where x = r2 s2 and y = 9rs, find ∂2z/(∂r ∂s). (compare with this example.)
Answers
To find ∂2z/(∂r ∂s), we need to take the partial derivative of ∂z/∂s with respect to r or the partial derivative of ∂z/∂r with respect to s.
Let's start by finding the partial derivatives of z with respect to x and y:
∂z/∂x = ∂f/∂x = 2r s2 ∂f/∂u (where u = x = r2 s2)
∂z/∂y = ∂f/∂y = 9r ∂f/∂v (where v = y = 9rs)
Next, we can use the chain rule to find the second partial derivative of z with respect to r and s:
∂2z/(∂r ∂s) = ∂/∂r (∂z/∂s)
= ∂/∂r (9s ∂f/∂v) (since ∂z/∂s = ∂f/∂y = 9r ∂f/∂v)
= 9 ∂/∂r (s ∂f/∂v)
= 9 (∂/∂v (s ∂f/∂u) * ∂u/∂r + ∂/∂v (s ∂f/∂v) * ∂v/∂r)
= 9 (s ∂2f/∂u∂v * 2rs + ∂f/∂v * 9)
= 18rs s ∂2f/∂u∂v + 81r ∂f/∂v
Therefore, the expression for ∂2z/(∂r ∂s) in terms of f(x,y) is:
∂2z/(∂r ∂s) = 18rs s ∂2f/∂u∂v + 81r ∂f/∂v, where u = x = r2 s2 and v = y = 9rs.
To know more about partial derivative refer here:
https://brainly.com/question/28750217?#
SPJ11
Related Questions
Use the Integral Test to determine whether the series is convergent or divergen sigma^infinity_n=1 ne^(-9n) Evaluate the following integral^infinity-1 xe^-9x dx.
Since the integral _______ finite, the series is_______
Answers
To use the Integral Test to determine whether the series is convergent or divergent, we need to evaluate the integral ∫(xe^(-9x) dx) from 1 to ∞.
Let's evaluate the integral first:
∫(xe^(-9x) dx) from 1 to ∞
We use integration by parts for this, where:
u = x, dv = e^(-9x) dx
du = dx, v = -1/9 e^(-9x)
According to the integration by parts formula, ∫u dv = uv - ∫v du.
So, ∫(xe^(-9x) dx) = -1/9 x e^(-9x) - ∫(-1/9 e^(-9x) dx)
Now, we can integrate -1/9 e^(-9x) dx:
∫(-1/9 e^(-9x) dx) = (-1/9) * (-1/9) * e^(-9x) = 1/81 e^(-9x)
Thus, our integral becomes:
-1/9 x e^(-9x) - 1/81 e^(-9x)
Now we must evaluate the integral from 1 to ∞:
lim (x→∞) [ -1/9 x e^(-9x) - 1/81 e^(-9x) ] - [ -1/9 (1) e^(-9) - 1/81 e^(-9) ]
Since the exponential term e^(-9x) approaches 0 as x approaches ∞, the limit becomes:
0 - [ -1/9 e^(-9) - 1/81 e^(-9) ] = 1/9 e^(-9) + 1/81 e^(-9)
Since the integral is finite, the series is convergent.
Visit here to learn more about Integral : https://brainly.com/question/18125359
#SPJ11
Ben has b dollars. Cam has 7 fewer dollars than Ben.
How many dollars does Cam have?
Answers
Answer:
Cam has b-7 dollars
Step-by-step explanation:
A farmer has 220 bushels of wheat to sell at her roadside stand. She sells an average of
16 and three eighths bushels each day. Represent the total change in the number of bushels she has for sale after
7 days.
Answers
Analyze the proportion below and complete the instructions that follow.
2x+5 x-5
3
4
Solve the proportion for x
A. -7
B. -4
C-2
D. -1
Answers
Answer:
A
Step-by-step explanation:
(2x + 5)/(3) = (x - 5)/(4)
Multiplying both sides by 12 to eliminate the fractions, we get:
4(2x + 5) = 3(x - 5)
Expanding the brackets, we get:
8x + 20 = 3x - 15
Subtracting 3x and 20 from both sides, we get:
5x = -35
Dividing both sides by 5, we get:
x = -7
Therefore, the solution to the proportion is x = -7.
So, the correct option is A) -7.
Which of the following is the complete list of roots for the polynomial function f(x)=(x2+6x+8)(x2+6x*13)
Answers
Solve to get x=-4, x=-2
Factorise x^2+6x+13=0 (I assumed you mistyped and wrote * instead of +)
Use the quadratic formula and you find that there are no real roots so the answer for this is just x=-4, x=-2
Tell me if I made any mistakes
how many 4-letter passwords can be formed using the letters a, b, c, d, e, f, g if repetition of letters is not allowed and the first letter can only be a, b or c?
Answers
840 are 4-letter passwords can be formed using the letters by permutation .
What are some examples of permutation?
A permutation is a set up of things in a specific order. In this arrangement, the components or components of sets are organized in a linear or sequential order. The permutation of the set A=1,6 is 2, for instance, 1,6, and 6,1. The components of set A cannot be arranged in any other way, as you can see.We are to count all possible 4-letter passwords that can be generated from the letters a, b, c, d, e, f, g .
There are 7 letters in total.
n = 7 r = 4
P(n , r ) = 7!/( n - r )!
P( 7 ,4 ) = 7!/( 7 - 4)!
= 7!/3!
= 7 * 6 * 5 * 4 * 3 * 2 * 1/3!
= 7 * 6 * 5 * 4
= 840
Learn more about permutation
brainly.com/question/1216161
#SPJ4
what is the image (-9,-2) after a reflection over the x-axis ?
Answers
Answer:
(-9,2)
Step-by-step explanation:
The rule for reflecting over the x axis is
(x,y)→(x,−y)
(-9, -2) becomes ( -9, - -2) = (-9,2)
Answer:
(-9,2)
Step-by-step explanation:
It will be -9,2 because when you reflect across x axis you change the y axis not the x axis because if you imagine it it works like that
Compare the probability that a randomly selected student is in grade 10 at each school. Move options to the blanks to complete thesentences.

Answers
From the question
The probability a student at school A is in grade 10 is
From the table
Number of students in grade 10 at school A = 25
Total number of students in School A = 120
Therefore
The probability a student at school A is in grade 10 is
\(\frac{25}{120}=\frac{5}{24}\)Hence, The probability a student at school A is in grade 10 is 5/24
The probability a student at school B is in grade 10 is
From the table
Number of students in grade 10 at school B = 20
Total number of students in School A = 80
Therefore
The probability a student at school B is in grade 10 is
\(\frac{20}{80}=\frac{1}{4}\)Hence, The probability a student at school B is in grade 10 is 1/4
Since, the probability a student at school B is in grade 10 is greater than the probability a tudent at school A is in grade 10 then
It is less like
the record high January temperature in Austin, Texas, is 90F. the record low January temperature is -2F. Find the difference between the high and low temperatures.
Answers
Answer:
92F
Step-by-step explanation:
the record high January temperature in Austin, Texas, is 90F. the record low January temperature is -2F. Find the difference between the high and low temperatures.
= 90 - (-2)
= 90 + 2
= 92F
The formula below gives the sum of the degrees, S, of the interior angles of a polygon. If n represents the number of sides, which equation solves for n?
S = (n-2) x 180
F. n = s/180 + 2
G. n = 180s + 2
H. n = s+2/180
J. n = (s+2) x 180
Answers
Answer: F. n = s/180 + 2
Step-by-step explanation:
To find the equation that solves for n, we will isolate the n variable.
Given:
S = (n - 2) x 180
Divide both sides of the equation by 180:
\(\frac{S}{180}\) = n - 2
Add 2 to both sides of the equation:
\(\frac{S}{180}\) + 2 = n
Reflexive property:
n = \(\frac{S}{180}\) + 2
F. n = s/180 + 2
What is the measure of

Answers
find the exact value of the trigonometric function at the given real number. (a) cos 19 6 (b) cos − 7 6 (c) cos − 11 6
Answers
The exact values of the trigonometric functions are (a) cos(19π/6) = √3/2,
(b) cos(-7π/6) = -√3/2, (c) cos(-11π/6) = -√3/2
How to find the exact values of the trigonometric functions at the given angles?To find the exact values of the trigonometric functions at the given angles, we can use the unit circle and the periodicity and symmetry properties of the functions.
(a) cos(19π/6):
First, we note that 19π/6 is equivalent to 18π/6 + π/6, which is equivalent to 3π + π/6. Since cosine has period 2π, we can reduce 3π to π and write:
cos(19π/6) = cos(3π + π/6) = cos(π/6) = √3/2
(b) cos(-7π/6):
We can use the symmetry property of cosine to write:
cos(-7π/6) = cos(π - 7π/6) = -cos(π/6) = -√3/2
(c) cos(-11π/6):
We can again use the symmetry property of cosine to write:
cos(-11π/6) = cos(π - 11π/6) = -cos(π/6) = -√3/2
Therefore, the exact values of the trigonometric functions are:
(a) cos(19π/6) = √3/2
(b) cos(-7π/6) = -√3/2
(c) cos(-11π/6) = -√3/2
Learn more about trigonometric
brainly.com/question/29156330
#SPJ11
Consider the linear program: Maximize z=−3x1+6x2, subject to: 5x1+7x2≤35
−x1+2x2≤2
x1≥0, x2≥0.
a) Solve this problem by the simplex method. Are there alternative optimal solutions? How can this be determined at the final simplex iteration? b) Solve the problem graphically to verify your answer to part (a).
Answers
Using the simplex method, the optimal solution for the given linear program is z = 14, with x1 = 0 and x2 = 5. There are no alternative optimal solutions.
To solve the linear program using the simplex method, we start by converting the problem into standard form with all constraints in the form of inequalities and non-negative variables. The initial tableau for the problem is as follows:
| x1 | x2 | s1 | s2 | b |
--------------------------------------------
z | -3 | 6 | 0 | 0 | 0 |
--------------------------------------------
s1| 5 | 7 | 1 | 0 | 35 |
--------------------------------------------
s2| -1 | 2 | 0 | 1 | 2 |
--------------------------------------------
Next, we perform the simplex iterations to improve the objective function value. After performing the necessary row operations, we arrive at the final tableau:
| x1 | x2 | s1 | s2 | b |
--------------------------------------------
z | 0 | 1 | 3/2 | -1/2 | 14 |
--------------------------------------------
s1| 0 | 0 | 4 | 3 | 5 |
--------------------------------------------
s2| 1 | 0 | -1/2 | 5/2 | 3 |
--------------------------------------------
From the final tableau, we can see that the optimal solution is z = 14, with x1 = 0 and x2 = 5. The decision variable x1 is at its lower bound, indicating that it is non-basic. Therefore, there are no alternative optimal solutions in this case.
In summary, the optimal solution for the given linear program is z = 14, with x1 = 0 and x2 = 5. There are no alternative optimal solutions.
Learn more about simplex method here:
brainly.com/question/15801083
#SPJ11
Which is the graph of g(x)?
3
x < -2
y
3,
g(x) = - + 2, -2 < x < 2
= Ž
2x - 3
.
X2

Answers
Answer:
The fourth graph to the right.
Step-by-step explanation:
A skating rink charges $75 for a nightly reservation as well as $5 per person skating. If n is the number of people skating, write an expression for the cost of reserving the rink.
Answers
Answer:
75+5n
Step-by-step explanation:
Solve with the cross multiplying
A.) X/25 = 24/100
X=
B.) X/44= 75/100
X=
Answers
Answer:
A) X= 6
B) X = 33
Step-by-step explanation:
Stationary points. Help ASAP please. Thanks
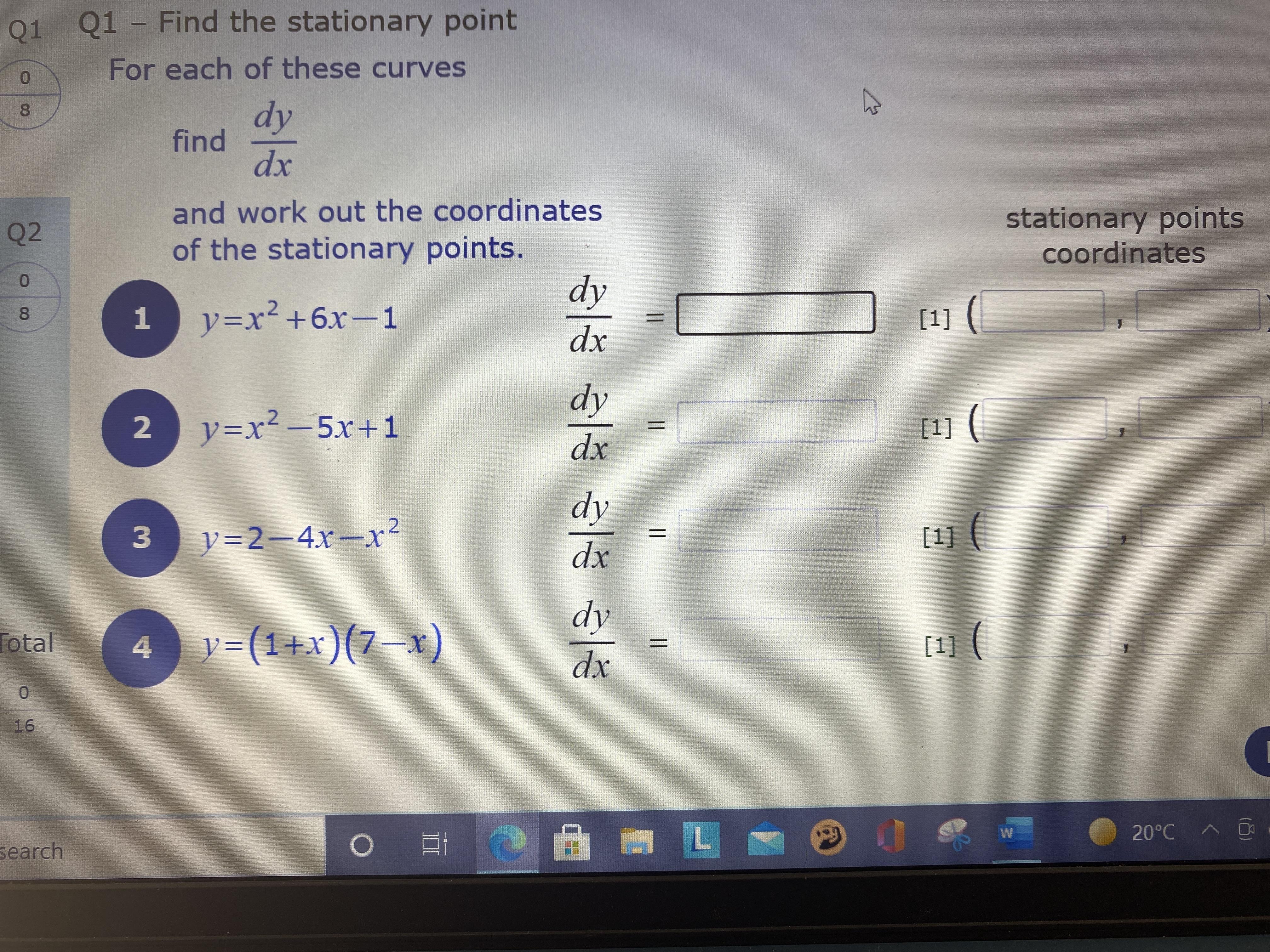
Answers
You can use the power rule for derivatives for each problem (though you could also use the product rule for the fourth curve).
y = x ² + 6x - 1 ==> dy/dx = 2x + 6
y = x ² - 5x + 1 ==> dy/dx = 2x - 5
y = 2 - 4x - x ² ==> dy/dx = -4 - 2x
y = (1 + x) (7 - x) = 7 + 6x - x ² ==> dy/dx = 6 - 2x
--
or, using the product rule,
dy/dx = (1 + x) (-1) + 1 (7 - x) = -1 - x + 7 - x = 6 - 2x
--
Now, stationary points occur where the derivative is zero. We have
2x + 6 = 0 ==> x = -3
2x - 5 = 0 ==> x = 5/2
-4 - 2x = 0 ==> x = -2
6 - 2x = 0 ==> x = 3
I need help on this answer now !!!!

Answers
Answer:
14
Step-by-step explanation:
substitute -2 into x in the equation
f(x) = -x^2 - 9x
f(-2) = -(-2)^2 - 9(-2)
f(-2) = 14 after calculation
I know it’s not 26 need help please

Answers
Answer:
x=11
Step-by-step explanation:
The angles are opposite interior angles and opposite interior angles are equal when the lines are parallel.
4x = 2x+22
Subtract 2x from each side
4x -2x = 2x+22-2x
2x = 22
Divide by 2
2x/2 =22/2
x = 11
NEED HELP ASAP - Algebra 2
Create your own instructions on how to simplify radical expressions. To accompany your explanation, create your own problem to show the steps in an example.
Answers
To simplify a radical expression, you can use a few different techniques. One common technique is to factor the expression under the radical sign (the radicand) as much as possible.
How to simplify radical expression?Another technique you can use is to use the properties of radicals. For example, you can use the product property of radicals to combine like terms under the radical sign
You can also use the quotient property of radicals to divide out a factor under the radical sign. Finally, some radicals are unsimplifiable by these methods. You can approximate a value of radical or try to get it in a form of fraction with radical.
Learn more about expressions on:
https://brainly.com/question/723406
#SPJ1
HELP PLEASE ANYONE I’m so lost

Answers
Answer:
x =4
Step-by-step explanation:
so pretty much you're give the values for theta and phi, so all you have to do is insert the values in their corresponding position and simplify it. After the simplification process, the answer should be no less or more than 4.
Answer:
the answer is 4
Step-by-step explanation:
by simplification;
=》
\( \frac{a + b}{a - b} \)
** putting the value of a and b :-
=》
\( \frac{5 + 3}{5 - 3} \)
=》
\( \frac{8}{2} \)
=》
\(4\)
As shown in the diagram below, Javier is standing outside next to a flagpole. Javier is 5'4" tall and his shadow is 40" long. The flagpole's shadow is 75" long. How tall is the flagpole?
Answers
Answer: Pretty sure 8 feet and 3 inches
Step-by-step explanation: I think this because 40 inches is 3 feet and 4 inches 5'4 - 2 feet is 3'4 so their is a 2 feet difference so the shadow is 75 inches long which is equal to 6'3 so you do 6'3+2feet you get you answer 8 feet 3 inches
solve for the indicated variable a/b = c for b
Answers
Answer:
b = \(\frac{a}{c}\)
Step-by-step explanation:
\(\frac{a}{b}\) = c ( multiply both sides by b )
a = bc ( isolate b by dividing both sides by c )
\(\frac{a}{c}\) = b
A candelabra holds 5 identical cylindrical
candles, each with a diameter of 6 centimeters
and a height of 9 centimeters. How many cubic
centimeters of wax are in all the candles on the
candelabra combined?
Answers
If an analysis of variance produces SS between = 20 and SS within = 40, then η 2 = 0.50.
true or false
Answers
Since η² ≈ 0.33 and not 0.50, the statement "If an analysis of variance produces SS between = 20 and SS within = 40, then η² = 0.50" is false.
ANOVA, or Analysis of Variance, is a statistical method used to compare the means of two or more groups to determine if there are any statistically significant differences between them. It is commonly used in experimental and observational studies to analyze the variance between group means and within-group variability.
ANOVA tests the null hypothesis that the means of the groups are equal, against the alternative hypothesis that at least one of the group means is different. It calculates the F-statistic, which compares the between-group variability to the within-group variability. If the F-statistic is large enough and exceeds a critical value, it indicates that there is evidence to reject the null hypothesis and conclude that there are significant differences between the group means.
We can determine if η² = 0.50 is true or false by calculating the effect size η² using the provided SS between and SS within values.
η² = SS_between / (SS_between + SS_within)
η² = 20 / (20 + 40)
η² = 20 / 60
η² = 1/3 ≈ 0.33
To know more about variance, visit:
https://brainly.com/question/31432390
#SPJ11
True, the eta-squared value is indeed 0.50, indicating that 50% of the total variance is accounted for by the between-group variation.
The formula to calculate eta squared (η2) is:
η2 = SSbetween / (SSbetween + SSwithin)
If SSbetween = 20 and SSwithin = 40, then:
η2 = 20 / (20 + 40) = 0.5
Therefore, η2 = 0.50, which means that 50% of the total variance in the dependent variable can be attributed to the independent variable (or factor) being analyze. The statement "If an analysis of variance produces SS between = 20 and SS within = 40, then η 2 = 0.50" is true. To determine η 2 (eta-squared), you'll need to calculate the proportion of total variance explained by the between-group variation. This can be done using the formula η 2 = SS between / (SS between + SS within). In this case, η 2 = 20 / (20 + 40) = 20 / 60 = 0.50. Therefore, the eta-squared value is indeed 0.50, indicating that 50% of the total variance is accounted for by the between-group variation.
To know more about variable visit:
https://brainly.com/question/15078630
#SPJ11
9. The regular price of an item at a store is p
dollars. The item is on sale for 20% off the regular
price. Some of the expressions shown below
represent the sale price, in dollars, of the item.
Expression A: 0.2p
Expression B: 0.8p
Expression C: 1 -0.2p
Expression D:p -0.2p
Which two expressions each represent the sal
price of the item?
A Expression A and Expression E
B Expression B and Expression C
C Expression B and Expression D
D Expression C and Expression D
Answers
Answer: C: Expression B and D
Step-by-step explanation:
Say the item is $100. 20% of 100 is equal to 100 (20/100)
When you simplify, it equals 20. So 20% of 100 is 20. This $20 is the amount of discount you receive.
So you have to subtract $20 from the $100 to find the sale price. The sale price is $80.
Now plug in 100 for p in each equation. The equation that equals 80 is the answer.
Only equation B and D equals 80 when 100 is plugged in.
Represent the following sentence as an algebraic expression, where "a number" is the letter x. You do not need to simplify. 2 is subtracted from the product of 5 and a number. 2 is subtracted from the product of 5 and a number.
Answers
The statement 2 is subtracted from the product of 5 and a number is
5x - 2.
What is a numerical expression?A numerical expression is a mathematical statement written in the form of numbers and unknown variables. We can form numerical expressions from statements.
Given, A statement an unknown number 'x' 2 is subtracted from the product of 5 and a number.
∴ 5×x - 2.
= 5x - 2 is the numerical expression.
learn more about numerical expressions here :
https://brainly.com/question/29199574
#SPJ1
A magician makes potions by combining maple syrup from a magical maple tree with ordinary water. The magician starts with a large supply of two potions: a red potion, which is 60% magical syrup by volume (and the rest is just water), and blue potion, which is 30% magical syrup by volume.
(a) Find the amount of red potion (in mL) that must be added to 500 mL of blue potion in order to produce potion that is 40% magical syrup by volume.
(b) Find the amounts of red potion and blue potion (in mL) that can be combined in order to produce 100 mL of a potion that is 54% magical syrup by volume.
(c) Does there exist a combination of red potion and blue potion that can produce a potion that is 75% magical syrup by volume?
need help
Answers
In system equation method,
a) Amount of red portion = 240 ml.
b) There are 300 mL of blue potion used and 100 mL of red potion used.
c) There is a ratio of 2 (blue potion):1 (red potion), there will be a 35% amount of magical syrup.
What is equation?
The definition of an equation in algebra is a mathematical statement that demonstrates the equality of two mathematical expressions. For instance, the equation 3x + 5 = 14 consists of the two equations 3x + 5 and 14, which are separated by the 'equal' sign.
(a) We can use a system equation here to solve this.
Let x=amount of red potion used
Let y=total amount of potion in solution
Then,
=>200 + x = y
=> 0.15(200) + 0.75x = 0.25y
0.15(200) because 15% of the blue potion=.15 and there is 200mL.
0.75x because 75% of the red potion=.75 and there is x amount of it
0.25y because we want 25% of the total potion=.25 and there is y amount of it.
We can substitute for y in the second equation:
=>0.15(200) + 0.75x = 0.25(200 + x)
=> 30 + 0.75x = 50 + 0.25x
=> -20 = -0.5x
=> x = 40
Knowing that x=40, we know that y=240, meaning our answer is 240.
b.) We can again use a system for this problem
Let x=Amount of red potion
Let y=Amount of blue potion
=> x + y = 400
=> 0.3(400) = 0.15y + 0.75x
0.3(400)=30% of the 400 mL
0.15y=15% of the magic syrup
0.75x=75% of the magic syrup
We can substitute for x in this equation:
=>120 = 0.15y + 0.75(400 - y)
120 = 0.15y + 300 - 0.75y
-180 = -0.6y
y = 300, x = 100
There are 300 mL of blue potion used and 100 mL of red potion used.
c.) Let x=amount of red potion
Let y=amount of blue potion
=> 0.15x + 0.75y = 0.35(x + y)
0.35(x+y) because the total amount of the potion is x+y
=>0.15x + 0.75y = 0.35x + 0.35y
0.4y = 0.2x
2y = x
Whenever there is a ratio of 2 (blue potion):1 (red potion), there will be a 35% amount of magical syrup.
To learn more about equation refer the below link
https://brainly.com/question/29336774
#SPJ1
Find the position and velocity of an object moving along a straight line with the given acceleration, initial velocity, and initial position. \[ a(t)=\sin \pi t, v(0)=4, s(0)=2 \] The velocity is \( \
Answers
The velocity function v(t) is -cos(πt)/π + (4 + 1/π) and the position function s(t) is -(sin(πt)/π²) + (4 + 1/π)t + 2.
To find the velocity and position of the object, we need to integrate the given acceleration function with respect to time.
Given: Acceleration function: a(t) = sin(πt)
Initial velocity: v(0) = 4
Initial position: s(0) = 2
To find the velocity function v(t), we integrate the acceleration function with respect to time:
v(t) = ∫ a(t) dt
Integrating sin(πt) with respect to t gives us:
v(t) = -cos(πt)/π + C
Using the initial velocity condition v(0) = 4, we can solve for the constant C:
v(0) = -cos(π(0))/π + C
4 = -cos(0)/π + C
4 = -1/π + C
C = 4 + 1/π
So, the velocity function v(t) becomes:
v(t) = -cos(πt)/π + (4 + 1/π)
To find the position function s(t), we integrate the velocity function with respect to time:
s(t) = ∫ v(t) dt
Integrating -(cos(πt)/π + (4 + 1/π)) with respect to t gives us:
s(t) = -(sin(πt)/π²) + (4 + 1/π)t + D
Using the initial position condition s(0) = 2, we can solve for the constant D:
s(0) = -(sin(π(0))/π²) + (4 + 1/π)(0) + D
2 = 0 + 0 + D
D = 2
So, the position function s(t) becomes:
s(t) = -(sin(πt)/π²) + (4 + 1/π)t + 2
To know more about function,
https://brainly.com/question/33431889
#SPJ11
Mr. Ramirez purchased 20 concert tickets for a total of $225. The concert tickets cost $15 for adults and $10 for children under the age of 12. What does the solution to the system of equations represent in the context of the problem
Answers
Answer:
do you want me to solve or what is it.
Step-by-step explanation: