ASAP! GIVING BRAINLIEST! Please read the question THEN answer CORRECTLY! NO guessing. I say no guessing because people usually guess on my questions.

Answers
Answer:
D. Yes; the graph passes the vertical line test.
Step-by-step explanation:
→The vertical line test is when you hold something (like a pencil), straight up/vertically, and you move it from left-to-right to see if any two points repeat.
→The correct answer is "D. Yes; the graph passes the vertical line test," because the x-values can't repeat, not the y-values, if the graph were to show a function. In this case, the graph passes the vertical line test.
Related Questions
If I make 10$ for working 6 hours if I wanted to make 8$ how many hours do I have to work
Answers
Answer:
4.8 hours
Step-by-step explanation:
6=10$
divide by 10
0.6=1$
multiply by 8
4.8=8$
Answer:
4.8
Step-by-step explanation:
Well, if you work for 6 hours, and earn 10$, then, you are earning 10/6$ per hour. So, we can estanblish the equation:
10/6$ * x hours = 8$.
x = 4.8 hours.
I need help with this I have 5 minutes to turn in

Answers
Answer:
y = 2x+1
Step-by-step explanation:
Multiply each value for x by 2and then add 1, it should equal the following value for y. For xample, if we take the first set of values: x = 3, y = 7:
y = 2x+1
7 = 2 x 3 + 1
7 = 6 + 1
7 = 7
The following works for all the sets.
if no values are repeated, then a data set doesn’t have a mode.
A. true
B. false
Answers
Sally is given $850. Every year, she decides to donate 9% of this money to charity until she has none left.
After 34 years, approximately how much money will Sally have left?
Answers
Answer:
Step-by-step explanation:
Year 1: $850 * 0.91 = $773.50
Year 2: $773.50 * 0.91 = $704.69
Year 3: $704.69 * 0.91 = $641.95
...
Year 34: (continue the pattern)
We can continue this calculation for each year, but to save time, we can use an exponential decay formula:
Remaining Amount = Initial Amount * (1 - rate)^years
Substituting the values:
Remaining Amount = $850 * (1 - 0.09)^34
Calculating this expression:
Remaining Amount ≈ $850 * (0.91)^34 ≈ $255.88
After 34 years, approximately $255.88 will be left with Sally.
Use the two given functions to write y as a function of x.
y = -3a + 3, a = -5x + 1
Answers
Answer:
Step-by-step explanation:
To write y as a function of x using the given functions, we can substitute the value of "a" in the first equation with the expression "-5x + 1" from the second equation.
Given:
y = -3a + 3
a = -5x + 1
Substituting the value of "a" in the first equation:
y = -3(-5x + 1) + 3
Now, let's simplify this expression:
y = 15x - 3 + 3
y = 15x
Therefore, y can be expressed as a function of x as:
y = 15x
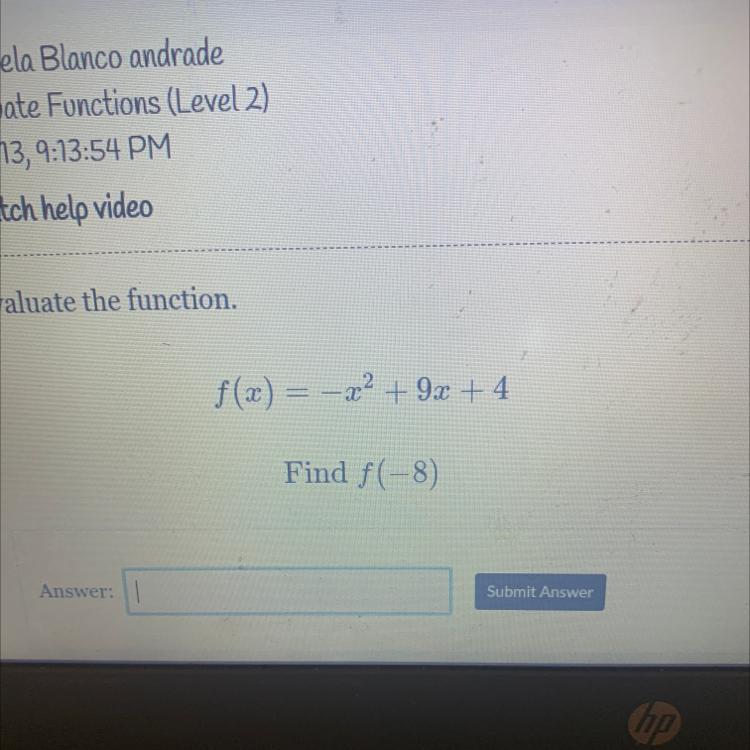
f(x) = –x^2 + 9x +4
Find f(-8)
I need help understanding this problem
Answers
\(▪▪▪▪▪▪▪▪▪▪▪▪▪ {\huge\mathfrak{Answer}}▪▪▪▪▪▪▪▪▪▪▪▪▪▪\)
let's find f(-8) :
\( - {x}^{2} + 9x + 4\)\( - ( - 8) {}^{2} + (9 \times ( - 8)) + 4\)\( - 64 - 72 + 4\)\( - 136 + 4\)\( - 132\)Can someone please help with 2 or 3 please !!

Answers
Step-by-step explanation:
2.
if parallel, the ratio of the line segments AD/DB must be the same as AE/AC.
4/2 = 2
but
9/5 is not 2 (10/5 would be 2).
so, they are not parallel.
3.
the area of a right-angled triangle is half the area of a rectangle with the same side lengths.
so, the area of ABC is
4×5/2 = 20/2 = 10
since D and E are midpoints, they are splitting the sides in half.
so, AD is only half as long as AC. the same for CE and CB.
so, the area of DEC is
2×2.5/2 = 5/2 = 2.5
the scale factor of the sides does apply to the area in a way, but not 1:1.
as the area is calculated by multiplying 2 sides, the scale factor is entering the calculation for each side and therefore twice. that means the scale factor is multiplied by itself.
so, the scale factor of the areas is in fact the square of the scale factor of the side lengths.
therefore, in our example here, the scale factor of the side lengths is 1/2. and the scale factor of the areas is (1/2)² = 1/4.
and indeed, 10× 1/4 = 10/4 = 2.5
Please help this is due today!!!!!
Given parallelogram FGHI determine the missing information
Don’t answer with one answer, blank or ridiculous answer please this is serious

Answers
Find the quotient of z₁ by z2. Express your answer in
trigonometric
form.
² - 3 (0 (4) + (*))
Z₁ cos
+/sin
Z₂
²2 = 7 (cos(377)+
COS
8
O A. 7 (cos (577) + i sin (5/77))
8
B.
21(cos(577)+isin (577))
8
OC. 21 cos
21(cos(-7)+ i sin(-77))
O D. 7 (cos(-7) + + sin(-7))
i
+/sin
37T
8

Answers
The quotient of z₁ by z₂ in trigonometric form is:
7/21 * (cos(584°) + i sin(584°))
To find the quotient of z₁ by z₂ in trigonometric form, we'll express both complex numbers in trigonometric form and then divide them.
Let's represent z₁ in trigonometric form as z₁ = r₁(cosθ₁ + isinθ₁), where r₁ is the magnitude of z₁ and θ₁ is the argument of z₁.
We have:
z₁ = 7(cos(577°) + i sin(577°))
Now, let's represent z₂ in trigonometric form as z₂ = r₂(cosθ₂ + isinθ₂), where r₂ is the magnitude of z₂ and θ₂ is the argument of z₂.
From the given information, we have:
z₂ = 21(cos(-7°) + i sin(-77°))
To find the quotient, we divide z₁ by z₂:
z₁ / z₂ = (r₁/r₂) * [cos(θ₁ - θ₂) + i sin(θ₁ - θ₂)]
Substituting the given values, we have:
z₁ / z₂ = (7/21) * [cos(577° - (-7°)) + i sin(577° - (-7°))]
= (7/21) * [cos(584°) + i sin(584°)]
The quotient of z₁ by z₂ in trigonometric form is:
7/21 * (cos(584°) + i sin(584°))
Option C, 21(cos(-7°) + i sin(-77°)), is not the correct answer as it does not represent the quotient of z₁ by z₂.
For more questions on trigonometric form
https://brainly.com/question/31744474
#SPJ8
Describe the Transformation and CHOOSE ALL THE
CORRECT ANSWERS! (MORE THAN 1 RIGHT
ANSWER).
f(x) = -2(x+3) 3 - 3
Answers
a boat travels 438 km in 8 hours with a constant speed, how far can it travel in 5 hours
Answers
Answer:
its the first one
Step-by-step explanation:
Why is the percent increase from 45 to 75 not equal to the percent decrease from 75 to45
Answers
Because a percent change is based on a comparison of the change in value the starting value and if the starting values are different, then the percent change is different.
When you increase from 45 to 75, you're comparing the change in value (30) to where you started (45).
When you decrease from 75 to 45, you're comparing the same amount of change (30) to a different starting value (75).
30/45 ≠ 30/75
if 2 (3x - 4 ) =5, then x =
Answers
Answer:
2.167 (rounded to the nearest hundredths).
Step-by-step explanation:
Isolate the variable, x. Note the equal sign, what you do to one side, you do to the other. Do the opposite of PEMDAS.
PEMDAS is the order of operations, and stands for:
Parenthesis
Exponents (& Roots)
Multiplication
Division
Addition
Subtraction
~
First, divide 2 from both sides of the equation:
(2(3x - 4))/2 = (5)/2
3x - 4 = 2.5
Next, isolate the variable, x. Add 4 to both sides of the equation:
3x - 4 (+4) = 2.5 (+4)
3x = 2.5 + 4
3x = 6.5
Then, divide 3 from both sides of the equation:
(3x)/3 = (6.5)/3
x = 6.5/3 = 2.167 (rounded).
~
Answer:
We have this equation
2*(3x-4) = 5
We can start solving the parentheses
2*(3x- 4) = 5
6x - 8 = 5
We can add 8 to both sides
6x - 8 + 8 = 5 + 8
6x = 13
And divide by 6
6x/6 = 13/6
x = 13/6
The following set of points are on the graph of a function:
x y
2 5
3 6
4 7
5 8
6 9
7 10
Which point would be on the inverse of this function?
Group of answer choices
(-10, -7)
(-6, -3)
(-2, -5)
(9, 6)
Answers
Point (9, 6) would be on the inverse of this function so option (D) will be correct.
What is a function?A certain kind of relationship called a function binds inputs to essentially one output.
A function can be regarded as a computer, which is helpful.
The machine will only accept specified inputs, described as the function's domain, and will potentially produce one output for each input.
Given the sets of coordinates of a function.
An inverse function is the reciprocal of a function and the coordinate of the inverse function is interchanged with the original function.
For example, if (x,y) is the coordinate of the function then (y,x) will be the coordinate of the inverse of the function.
Since option (D) (9, 6) is the interchange of (6,9) so it will be the inverse of a function.
Hence "Point (9, 6) would be on the inverse of this function".
For more about the function,
brainly.com/question/23712366
#SPJ2
Estimate the slope of the tangent line (rate of change) to f(x) = ² at x = -1 by finding the slopes of
the secant lines through the points:
a. (-2,4) and (0,0)
secant slope, msec=
b. (-1.5, 2.25) and (-0.5, 0.25)
secant slope, msec=

Answers
a. The secant slope through (-2,4) and (0,0) is -2.
b. The secant slope through (-1.5,2.25) and (-0.5,0.25) is -2.
The estimated slope of the tangent line to f(x) = x^2 at x = -1 is approximately -2.
To estimate the slope of the tangent line to the function f(x) = x^2 at x = -1, we can find the slopes of the secant lines through different pairs of points.
a. (-2,4) and (0,0):
The coordinates of the two points are (-2, 4) and (0, 0). We can calculate the slope of the secant line passing through these points using the formula:
msec = (y2 - y1) / (x2 - x1)
Plugging in the values, we get:
msec = (0 - 4) / (0 - (-2))
= -4 / 2
= -2
So, the slope of the secant line passing through (-2, 4) and (0, 0) is -2.
b. (-1.5, 2.25) and (-0.5, 0.25):
The coordinates of the two points are (-1.5, 2.25) and (-0.5, 0.25). Using the slope formula, we can calculate the slope of the secant line passing through these points:
msec = (0.25 - 2.25) / (-0.5 - (-1.5))
= (-2) / (1)
= -2
So, the slope of the secant line passing through (-1.5, 2.25) and (-0.5, 0.25) is -2.
By finding the slopes of the secant lines, we have estimated the rate of change of the function f(x) = x^2 at x = -1. The slope of the tangent line at this point will be very close to these secant slopes, particularly as the two points used to calculate the secant lines get closer together.
for such more question on secant slope
https://brainly.com/question/27877215
#SPJ8
HELPPPP, answer the picture first and then the question. If you get the answer correct you get BRAINLIEST.
Using your graphing calculator skills you've been developing, answer the question below using a graph(s) of the functions above:
Is there a point Maria will start losing money (making a negative profit)? If there is, when would that be?

Answers
well, let's recall that Profit is Revenue - Costs, in essence, subtracting what you spent to make the product from the amount you charge, whatever the surplus amount is, goes by the name of "profit".
\(P(t)~~ = ~~\stackrel{S(t)}{(-4t^2+48t)}~~ - ~~\stackrel{M(t)}{(-3t^2+36t)} \\\\\\ P(t)=-4t^2+48t+32t^2-36t\implies \boxed{P(t)=-t^2+12t}\)
Check the picture below.
is there a point when Maria is losing money?
well, from the graph, if we to say the origin, that (0,0), there's no profit, profit is 0, now, if we go to the left of that, the line is going to the negative, so we can say if makes "negative t-shirts" hehe, namely, if she starts to give them away like there's no tomorrow, then hell she's in the red ink, now if we go beyond t = 12, the graph goes back down again? the hell? well, that just means that if she makes t-shirts for more than 12 days, she's back in the red ink again,.

(q1) Find the length of the curve described by the function

Answers
The value of the Integral at the lower limit from the value of the integral at the upper limit to get the length of the curve.
The length of the curve described by the function f(x) = 1 + 3x^2 + 2x^3 is to be found. The formula used to find the length of a curve is:
L = ∫(sqrt(1 + [f'(x)]^2))dx where f'(x) is the derivative of f(x)We have to first find f'(x):f(x) = 1 + 3x^2 + 2x^3f'(x) = 6x + 6x^2
The integral becomes:L = ∫(sqrt(1 + [6x + 6x^2]^2))dx = ∫(sqrt(1 + 36x^2 + 72x^3 + 36x^4))dx The integral appears to be difficult to evaluate by hand.
Therefore, we use software like Mathematica or Wolfram Alpha to solve the problem. Integrating the expression using Wolfram Alpha gives:
L = 1/54(9sqrt(10)arcsinh(3xsqrt(2/5)) + 2sqrt(5)(2x^2 + 3x)sqrt(9x^2 + 4))The limits of integration are not given. Therefore, the definite integral be solved.
We can, however, find a general solution. We use the above formula and substitute the limits of integration.
Then, we subtract the value of the integral at the lower limit from the value of the integral at the upper limit to get the length of the curve.
To know more about Integral.
https://brainly.com/question/27419605
#SPJ8
B
А
С
T
D
© 2016 Strong Mind. Created using GeoGebra.
In circle T, m AB = (3x + 9° and mCD = (11x – 71).
What is the measure of AB?
61°
37°
10°
39°
Answers
Answer:
D. 39°
Step-by-step explanation:
mAB = (3x + 9°)
mCD = (11x – 71)
From the diagram: |AB|=|CD|
Since arcs AB and CD are subtended by a chord of equal length.
mAB=mCD
3x + 9°=11x – 71°
Collect like terms to solve for x
11x-3x=9°+71°
8x=80°
x=10°
Therefore, the measure of AB:
mAB = (3x + 9°)
=3(10)+9
=30+9
=39°
The correct option is D.

Which of these expressions is equivalent to log (26.35)?
OA. log (26) - log (35)
OB. log (26) + log (35)
OC. log (26) log (35)
●
OD. 26 log (35)
Answers
Answer:
log(ab)=loga+logb
•log26.35=log26+log35
B.log26+log35
50 POINTS !!
PLEASE HELP !! ILL GIVE BRAINLIEST TO THE RIGHT ANSWERS.

Answers
Answer:
60
Step-by-step explanation:
you can use the equations for the pythagorean theorem which is a^2 + b^2 =c^2. plug in the numbers you know and then you figure out what yhe missing value is.
Riley put £450 into a savings account which
gathered simple interest at a rate of 2% per month.
After 6 months, Riley used some of the money in
the account to buy a bike costing £480.
How much money did Riley have left?
Answers
Answer:
£26.77
Step-by-step explanation:
450(100% + 2%)^6
= 450 (1.02)^6
= 506.77.
506.77 - 480 - 26.77.
Riley had £26.77 left.
Among all pairs of numbers whose sum is 24, find a pair whose product is as large as possible. Show the work(the steps)! Write an equation of the corresponding quadratic function. How parabola opens? What is the maximum product? Does this function has a maximum value or the minimum value? Explain. Graph the function and upload the image.
Answers
The pair of numbers that yields the maximum product when their sum is 24 is (12, 12), and the maximum product is 144. The corresponding quadratic function is P(x) = -x^2 + 24x, and the parabola opens downwards.
To find a pair of numbers whose sum is 24 and whose product is as large as possible, we can use the concept of maximizing a quadratic function.
Let's denote the two numbers as x and y. We know that x + y = 24. We want to maximize the product xy.
To solve this problem, we can rewrite the equation x + y = 24 as y = 24 - x. Now we can express the product xy in terms of a single variable, x:
P(x) = x(24 - x)
This equation represents a quadratic function. To find the maximum value of the product, we need to determine the vertex of the parabola.
The quadratic function can be rewritten as P(x) = -x^2 + 24x. We recognize that the coefficient of x^2 is negative, which means the parabola opens downwards.
To find the vertex of the parabola, we can use the formula x = -b / (2a), where a = -1 and b = 24. Plugging in these values, we get x = -24 / (2 * -1) = 12.
Substituting the value of x into the equation y = 24 - x, we find y = 24 - 12 = 12.
So the pair of numbers that yields the maximum product is (12, 12). The maximum product is obtained by evaluating the quadratic function at the vertex: P(12) = 12(24 - 12) = 12(12) = 144.
Therefore, the maximum product is 144. This quadratic function has a maximum value because the parabola opens downwards.
To graph the function, you can plot several points and connect them to form a parabolic shape. Here is an uploaded image of the graph of the quadratic function: [Image: Parabola Graph]
For more such question on function. visit :
https://brainly.com/question/11624077
#SPJ8
Simplify 3\(\sqrt\)2-√2
Answers
Answer: (√2)(2) = 2√2
Step-by-step explanation:
To simplify the expression 3√2 - √2, you can factor out the common term √2:
3√2 - √2 = (√2)(3 - 1)
Now, subtract the numbers in parentheses:
(3 - 1) = 2
(√2)(2) = 2√2
Find the area of a circle whose radius is
52 km. Round to nearest tenth
Answers
Answer:
8494.87 is the actual answer but the rounded version is 8494.9
Step-by-step explanation:
3.142×52^2=8494.866535
8494.9 nearest tenth
Sam is climbing 9000 m every 30 minutes. How many meters will he climb in 1 hour
Answers
Answer:
18000 m
Step-by-step explanation:
Hey there!
In order to solve this problem, we need to first know how many minutes are in an hour
As you know, there are 60 minutes in an hour so this means in 1 hour, he will climb 9000 meters two times
So 9000 two times is 18000,
Meaning, in 1 hour, Sam will climb 18000 m
Answer:
18,000m in an hour
Step-by-step explanation:
We know this because if its 9000 m in 30 minutes, we can do 9000 x 2 and get 18,000m for an hour.
Complete the following sentence.
When a system of measurement is based on units of ten, it is called a________ system.
Answers
Answer:
it is called a decimal system
Step-by-step explanation:
.
Answer:
Decimal system
Solve for x, y, and z

Answers
Step-by-step explanation:
\(x = 46.16 \\ y = 23.00 \\ z = 55.7\)
PLEASE PLEASE HELP!!! WIL GIVE BRAINLYEST: find the perimeter and area of the square

Answers
Assuming the 6 is the entire value on the right and it wasn't cut off...
Perimeter: Add up all the side lenghts, as if you were walking around the rectangle.
perimeter = top + right side + bottom + left side
= 3x+4 + 6 + 3x+4 + 6
= 6x + 20
Area: Multiply the length times the width.
area = top • right side
= (3x+4) • 6
= 18x + 24 using distribution
what is the period of the since function y=sin(4x)?

Answers
Answer:
C π/2
Step-by-step explanation:
Amplitude: 1
Period: π2
Phase Shift: None
Vertical Shift: None
Mid topic checkpoint chapter 4 for questions 3,and 4

Answers
3) The equation of the linear model would be y = 7.5x+60.
4) If Adam studies for 6 hours then his score would be 88.
What is the Linear equation?
An algebraic equation with only a constant and a first-order (linear) term is said to be linear if it has the formula y = mx + b, where m is the slope and b is the y-intercept. The above is occasionally referred to as a "linear equation with two variables," where y and x are the variables.
y = mx + c
where m denotes the slope.
The y-intercept is represented by the constant c. (Where x is zero)
In our instance, y-intercept equals 60.
The line's equation will therefore be:
y = mx + 60
y = mx + 60
There are given the line's coordinates (4, 90). These considerations will thus satisfy the equation.
90 = 4*m + 60
4.m = 30 m = 7.5 m = 7.5 y = 7.5x + 60 y = 7.5 * 6 + 60 y = 45 + 60 y = 105 is
y = 7.5x + 60.
If Adam's study for 6 hours then his score would be
y = 7.5x + 60.
y = 7.5(6) + 60
y = 105
Hence,
3) The equation of the linear model would be y = 7.5x+60.
4) If Adam studies for 6 hours then his score would be 88.
To learn more about equations refer to:
brainly.com/question/4344214
#SPJ1