As part of a science experiment, a student observes the growth of a population of bacteria in four different media. The table below lists the observations the student made.
Medium
Observation
1
Population increases by 10 every hour
II
Population decreases by 10 every hour
THI Population increases by 10% overy hour
M Population decreases by 10% every hour
In which media can the change in the population of bacteria be modeled by a linear function?
media I and II
media I and III
media II and IV
media III and IV
Answers
Answer:
Step-by-step explanation:
Here is the graph and I’m not sure if my answer is correct or not

Related Questions
You are a camp counselor and have 2/3 pound of fishing bait. If you give each
camper 1/6 pound, how many campers receive bait? Before you model and
solve this problem, estimate your answer.
Write a division expression that would represent the situation above.
Answers
C = amount of campers
so, if we give each campler 1/6 lb evenly, whatever that sum will just add up to 2/3 lb.
If we have "C" campers, the product of 1/6 * C gives use that sum, so we can say that
\(\cfrac{1}{6}C~~ =~~\cfrac{2}{3}\implies C = \cfrac{~~ \frac{2}{3}~~}{\frac{1}{6}}\implies C = \cfrac{2}{3}\div \cfrac{1}{6}\implies C = \cfrac{2}{\underset{1}{~~\begin{matrix} 3 \\[-0.7em]\cline{1-1}\\[-5pt]\end{matrix}~~}}\cdot \cfrac{\stackrel{2}{~~\begin{matrix} 6 \\[-0.7em]\cline{1-1}\\[-5pt]\end{matrix}~~}}{1}\implies C = 4\)
Find the slope of the line that passes through the pair of points (-1,-9) and (-3,10)
Answers
Answer:
-9.5
Step-by-step explanation:
The slope (m) is the ratio of the change in y to the change in x:
m = (y2 -y1)/(x2 -x1)
m = (10-(-9))/(-3-(-1)) = 19/-2
m = -9.5
The slope of that line is -9.5.
__
The graph shows the line through those points, written in point-slope form.

You earn $7.50 per hour and need to earn $35. Write and solve an inequality to find how many hours you must work
Answers
Answer:
7.50 x = 35 Answer is around 4.6 hours
Step-by-step explanation:
Divide 35 by 7.50 to find the number of hours.
Hope this helps! If it does, please mark me brainliest! Thank you! ;)
If a seed is planted, it has a 85% chance of growing into a healthy plant.
If 9 seeds are planted, what is the probability that exactly 4 don't grow? Round to 4 decimals.
Answers
The probability that exactly 4 seeds out of 9 planted won't grow is 1.57%.
What is the probability that 4 seeds won't grow?Let X be the number of seeds that don't grow.
X follows a binomial distribution with parameters n=9 and p=0.15 (the probability that a seed doesn't grow).
So, probability of exactly 4 seeds not growing is:
P(X=4) = \(9C4 * (0.15)^4 * (1-0.15)^5\)
P(X=4) = 70 * 0.00050625 * 0.4437053125
P(X=4) = 0.01572380701
P(X=4) = 1.57%
Read more about probability
brainly.com/question/24756209
#SPJ1
The sum of two consecutive even integers is at most 400. The pair of integers with the greatest sum is 196 and 198. True or Flase
Answers
Answer:
False
Step-by-step explanation:
The greatest sum of two consecutive even integers would be 200 + 198, or 398
Answer:
its true
Step-by-step explanation:
If f(x) is a function which is continuous everywhere then we must have m= ?

Answers
The function is continuous only if m = 7.
How to find the value of m?If the function is continue, then the value of the function needs to be the same one in both pieces of the function when we evaluate in x = -2
That means that:
f(-2) = f(-2) (trivially)
Replacing the two pieces of the function we will get:
m*(-2) - 6 = (-2)^2 + 10*(-2) - 4
now we can solve that equation for m.
-2m - 6 = 4 -20 - 4
-2m = -20 + 6 = -14
m = -14/-2 = 7
m = 7
that is the value of m.
Laern more about continuous functions at:
https://brainly.com/question/18102431
#SPJ1
please help I don't get it NO LINKS or I'll report pls don't answer the question if u don't know

Answers
Answer:
1 person got 68 inches
4 persons got 69 inches
2 persons got 70 inches
3 persons got 74 inches
1 person got 76 inches
i need help!!!! does anyone know this..!!???

Answers
The period of oscillation is 3 seconds
What is period of oscillation?A Oscillation is the periodic change of a measure around a central value or between two or more states, usually in time.
The time taken for an oscillating particle to complete one cycle of oscillation is known as the Period of oscillating particle. It is measured in seconds
Oscillation can also be vibration or revolution or cycle.
Therefore, using the graph to determine the period. Then the wave particle made a complete oscillation at 3 second.
This means that the period of the particle is 3 seconds.
learn more about period of oscillation from
https://brainly.com/question/22499336
#SPJ1
What is cos(tan^-1(-2/3))=
Answers
cos(tan^(-1)(-2/3)) simplifies to 3√13 / 13.
To evaluate the expression cos(tan^(-1)(-2/3)), we can use the trigonometric identity:
cos(tan^(-1)(x)) = 1 / √(1 + x^2)
In this case, x is -2/3. Substituting the value into the identity:
cos(tan^(-1)(-2/3)) = 1 / √(1 + (-2/3)^2)
Now, let's calculate the value:
cos(tan^(-1)(-2/3)) = 1 / √(1 + 4/9)
= 1 / √(13/9)
= 1 / (√13/3)
= 3 / √13
= 3√13 / 13
For more such quaetions on simplifies
https://brainly.com/question/29369267
#SPJ8
Triangle A'B'C' is formed using the translation (x + 1. y + 1) and the dilation by a scale factor of 3 from the origin. Which equation explains the relationship
between BC and B"C"?
CI
OB"C" -
3
OBC
B"C"
3
B"C"
BC
BC

Answers
Answer:
d
Step-by-step explanation:
(x, y) ⇒ (x + 1, y +1) ⇒ (3x, 3y)
A (-3, 3) ⇒ A' (-2, 4) ⇒ A'' (-6, 12)
B (1, -3) ⇒ B' (2, -2) ⇒ B'' (6, -6)
C (-3, -3) ⇒ C' (-2, -2) ⇒ C'' (-6, -6)
The relationship between BC and B"C" is B"C"/BC = 1/3 if the triangle A'B'C' is formed using the translation (x + 1. y + 1) and the dilation by a scale factor of 3 from the origin. option (C) is correct.
What is geometric transformation?It is defined as the change in coordinates and the shape of the geometrical body. It is also referred to as a two-dimensional transformation. In the geometric transformation, changes in the geometry can be possible by rotation, translation, reflection, and glide translation.
We have:
Triangle A'B'C' is formed using the translation (x + 1. y + 1) and the dilation by a scale factor of 3 from the origin.
As we know, the ratio among comparable dimensions of an object and a model with that object is known as an exponent in algebra. The replica will be larger if the scale factor is a whole number. The duplicate will be lowered if the step size is a fraction.
The scale factor k = 1/3
B"C" = kBC
B"C" = BC/3
B"C"/BC = 1/3
Thus, the relationship between BC and B"C" is B"C"/BC = 1/3 if the triangle A'B'C' is formed using the translation (x + 1. y + 1) and the dilation by a scale factor of 3 from the origin. option (C) is correct.
Learn more about the geometric transformation here:
brainly.com/question/16156895
#SPJ5
Given:
AD
diameter of Circle P.
Dec
B
A
If m < 1 = 30°, then m AB
15
30
60

Answers
Answer:
The measure of an arc is the size of the corresponding central angle, so angle 1 for AB,
Answer: B 30
Select all solutions to M•M•M=729
Answers
The solution to the equation given by M * M * M = 729 is 9
What is an equation?An equation is an expression that shows the relationship between two or more numbers and variables using mathematical operations. An equation can be linear, quadratic, cubic and so on, depending on the degree of the variable.
Given the equation:
M.M.M = 729
This gives:
M * M * M = 729
M³ = 729
Taking the cube root of both sides:
∛M³ = ∛729
M = 9
The solution to the equation is 9
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
Airline travelers should be ready to be more flexible as airlines once again cancel thousands of flights this summer. The Coalition for Airline Passengers Rights, Health, and Safety averages 400 calls a day to help stranded travelers deal with airlines (seattlepi.com, July 10, 2008). Suppose the hotline is staffed for 16 hours a day. a. Calculate the average number of calls in a one-hour interval; 30-minute interval; 15-minute interval. (Round your answers to 2 decimal places.) Interval Average Number of Calls 60-minute 30-minute 15-minute b. What is the probability of exactly 6 calls in a 15-minute interval? (Round your intermediate calculations and final answer to 4 decimal places.) Probability c. What is the probability of no calls in a 15-minute interval? (Round your intermediate calculations and final answer to 4 decimal places.) Probability d. What is the probability of at least two calls in a 15-minute interval? (Round your intermediate calculations and final answer to 4 decimal places.) Probability
Answers
The Coalition for Airline Passengers Rights, Health, and Safety averages 400 calls a day to help stranded travelers deal with airlines. The hotline is staffed for 16 hours a day.
To calculate the average number of calls in different time intervals and the probability of different events related to these calls.
Part 1:
a. 60-minute interval average number of calls: 400/16 = 25 calls
30-minute interval average number of calls: 25/2 = 12.5 calls
15-minute interval average number of calls: 12.5/2 = 6.25 calls
Part 2:
b. To find the probability of exactly 6 calls in a 15-minute interval, we can use the Poisson distribution formula. Let's assume that the average number of calls in a 15-minute interval is 6.25. Then, the probability of exactly 6 calls in a 15-minute interval is:
P(6 calls) = (e^-6.25)*(6.25^6)/6! = 0.0686
c. To find the probability of no calls in a 15-minute interval, we can use the Poisson distribution formula. Let's assume that the average number of calls in a 15-minute interval is 6.25. Then, the probability of no calls in a 15-minute interval is:
P(0 calls) = e^-6.25 = 0.0047
d. To find the probability of at least two calls in a 15-minute interval, we can use the cumulative distribution function of the Poisson distribution. Let's assume that the average number of calls in a 15-minute interval is 6.25. Then, the probability of at least two calls in a 15-minute interval is:
P(X >= 2) = 1 - P(0 calls) - P(1 call) = 1 - 0.0047 - (e^-6.25)*(6.25^1)/1! = 0.9906
Thus, the average number of calls in a 60-minute interval is 25, in a 30-minute interval is 12.5, and in a 15-minute interval is 6.25. The probability of exactly 6 calls in a 15-minute interval is 0.0686, the probability of no calls in a 15-minute interval is 0.0047, and the probability of at least two calls in a 15-minute interval is 0.9906.
Learn more about Probability here brainly.com/question/11234923
#SPJ4
A farmer earns $___ for each orange she sells. She had to pay $___ for fertilizer. Part A: Rewrite the description by filling in the blanks with values of your choice to show the amount of money the farmer could earn selling any number of oranges, n. Make sure the values you choose make sense for this situation. (6 points) Part B: Write an algebraic expression from your written description used in Part A. Let n stand for the number of oranges. (6 points)
Answers
Part B: The algebraic expression for the amount of money the farmer could earn selling any number of oranges, n, is 0.20n - 25.
I'm on a team of 9 people and we told our
teacher that together we could eat 36 Cloud
cupcakes. So I'd like to buy my fair share of that
36.
Answers
The number of Cloud cupcakes that each person will be 4.
What is Algebra?Algebra is the study of abstract symbols, while logic is the manipulation of all those ideas.
The acronym PEMDAS stands for Parenthesis, Exponent, Multiplication, Division, Addition, and Subtraction. This approach is used to answer the problem correctly and completely.
I'm on a team of 9 people and we told our teacher that together we could eat 36 Cloud cupcakes.
The number of Cloud cupcakes that each person will be given as,
⇒ 36 / 9
⇒ 4
The number of Cloud cupcakes that each person will be 4.
More about the Algebra link is given below.
https://brainly.com/question/953809
#SPJ1
Given: \angle ADE \cong \angle CDE∠ADE≅∠CDE and \overline{BD}
BD
bisects \angle ABC.∠ABC.
Prove: \overline{AB} \cong \overline{CB}
AB
≅
CB
.
Answers
∠ADE≅∠CDE and BD bisects ∠ABC.
Since BD bisects ∠ABC, it follows that ∠ABD = ∠CBD. (angle bisector theorem)
By the Angle-Angle-Side (AAS) congruence theorem, since ∠ADE and ∠CDE are congruent, and ∠ABD = ∠CBD, then ∠ABE = ∠CBE.
Therefore, by the Side-Angle-Side (SAS) congruence theorem, since ∠ABE = ∠CBE, and AB = CB, then AB ≅ CB.
In simple terms, what is an angle?A figure that is created by two rays or lines that have the same endpoint is known as an angle in plane geometry. From the Latin word "angulus," which meaning "corner," comes the English term "angle." The vertex, which is the shared terminal of the two rays, is referred to as the side of an angle.
How Do You Measure An Angle?To measure angles, we employ protractors. View the AOB figure provided below. Let's try to determine what kind of angle AOB is. It appears to be at an acute angle, doesn't it? This indicates that its measure is more than 0° and less than 90°. Let's practice using the protractor to measure this angle.
To know more about angle visit:
https://brainly.com/question/28451077
#SPJ1
Find the complement and the supplement of the given angle. 26°
The complement of the angle is ??
Answers
Step-by-step explanation:
the complement of 26 degree is (90-26).
The supplement of (90-26) is 180 ( 90-26) = 116 degree
Hey there!
Complementary angles add up to
\(\bold{90^\circ}\).
Supplementary angles add up to
\(\bold{180^\circ}\).
We are given an angle whose measure is
\(\bold{26^\circ}\)
The complement of that angle is
\(\bold{x+26=90}\)
Subtract & find the complement
\(\bold{x=64^\circ}\)
Now let's find the supplement of the angle
\(\bold{x+26=180}\)
Subtract and find the supplement
\(\bold{x=154^\circ}\)
Hope everything is clear.
Let me know if you have any questions!
#KeepLearningWithJoy
Answer Given By
\(\boxed{ST2710~}\)
Or
A felicitous teenager Willing To Assist OthersHave an outstanding day!
help. use the figure shown to the right to find the value of x

Answers
Answer:
\(\begin{aligned}x &= 16\sqrt3 \\ &\approx 27.7\end{aligned}\)
Step-by-step explanation:
We can see that the longer leg (a) of a right triangle is half of the circle's radius. Since we are given the other two sides of the triangle (shorter leg and hypotenuse), we can solve for the length of the longer leg using the Pythagorean Theorem:
\(a^2 + b^2 = c^2\)
↓ plugging in the given values
\(a^2 + 2^2 = 14^2\)
↓ subtracting 2² from both sides
\(a^2 = 14^2 - 2^2\)
\(a^2 = 196 - 4\)
\(a^2 = 192\)
↓ taking the square root of both sides
\(a = \sqrt{192\)
↓ simplifying the square root
\(a = \sqrt{2^6 \cdot 3\)
\(a = 2^{\, 6 / 2} \cdot \sqrt3\)
\(a = 2^3\sqrt3\)
\(a = 8\sqrt3\)
Now, we can solve for the radius (x) using the fact that the longer leg of the triangle is half of it.
\(a = \dfrac{1}{2}x\)
↓ plugging in the a-value we solved for
\(8\sqrt3 = \dfrac{1}2x\)
↓ multiplying both sides by 2
\(\boxed{x = 16\sqrt3}\)
2) The mean mathematics SAT score in 2012 was 514 with a standard deviation of 117 ("Total group profile," 2012). Assume the mathematics SAT score is normally distributed. a. State the random variable. b. Find the probability that a person has a mathematics SAT score over 700. c. Find the probability that a person has a mathematics SAT score of less than 400. d. Find the probability that a person has a mathematics SAT score between a 500 and a 650. e. Find the mathematics SAT score that represents the top 1% of all scores.
Answers
The mathematics SAT score representing the top 1% of all scores is approximately 780.
a. The random variable in this case is the mathematics SAT score.
b. To find the probability that a person has a mathematics SAT score over 700, we need to calculate the z-score first.
The z-score is calculated as \(\frac{(X - \mu )}{\sigma}\),
where X is the value we're interested in, μ is the mean, and σ is the standard deviation.
In this case, X = 700, μ = 514, σ = 117.
Using the formula, the z-score is \(\frac{(700 - 514)}{117 } = 1.59\).
To find the probability associated with this z-score, we can consult a standard normal distribution table or use a calculator.
The probability is approximately 0.0564 or 5.64%.
c. To find the probability that a person has a mathematics SAT score of less than 400, we again calculate the z-score using the same formula.
X = 400, μ = 514, and σ = 117.
The z-score is \(\frac{(400 - 514) }{117 } = -0.9744\).
Looking up the probability associated with this z-score, we find approximately 0.1635 or 16.35%.
d. To find the probability that a person has a mathematics SAT score between 500 and 650, we need to calculate the z-scores for both values.
Using the formula, the z-score for 500 is \(\frac{(500 - 514)}{117 } = -0.1197\),
and the z-score for 650 is \(\frac{(650 - 514)}{117 } = 1.1624\).
We can then find the area under the normal curve between these two z-scores using a standard normal distribution table or calculator.
Let's assume the probability is approximately 0.3967 or 39.67%.
e. To find the mathematics SAT score that represents the top 1% of all scores, we need to find the z-score corresponding to the top 1% of the standard normal distribution.
This z-score is approximately 2.33.
We can then use the z-score formula to calculate the corresponding SAT score.
Rearranging the formula,
\(X = (z \times \sigma ) + \mu\),
where X is the SAT score, z is the z-score, μ is the mean, and σ is the standard deviation.
Substituting the values,
\(X = (2.33 \times 117) + 514 = 779.61\).
Rounded to the nearest whole number, the mathematics SAT score representing the top 1% of all scores is approximately 780.
For such more questions on mathematics
https://brainly.com/question/29892643
#SPJ8
Given: tangent to Circle O.
If m = 140°, then A =
Answers
The measure of the angle A is 70 degrees if the DR is the tangent to the circle option (A) 70 degrees is correct.
What is a circle?It is described as a set of points, where each point is at the same distance from a fixed point (called the center of a circle)
The question is incomplete.
The complete question is in the picture, please refer to the attached picture.
It is given that:
Join the points B and O and then join points D and O
Angle A = (1/2)Angle BOD
Angle B = 140 degrees
Angle A = (1/2)140 degrees
Angle A = 70 degrees
Thus, the measure of the angle A is 70 degrees if the DR is the tangent to the circle option (A) 70 degrees is correct.
Learn more about circle here:
brainly.com/question/11833983
#SPJ1

EASY POINTS!
Which equation represents the image of the line y = 3x +1 after a translation of 3 units on the x-axis?
Answers
The equation represents the image of the line y = 3x +1 is y' = 3(x - 3) +1.
What is Translation?Each point in a figure is moved the same distance in the same direction using a type of transformation known as translation.
For example, this transformation moves the parallelogram to the right 5 units and up 3 units. It is written ( x , y ) → ( x + 5 , y + 3 ) .
Given:
The transformation that translates function y = f(x) by h units right and k units up is
y' = f(x -h) +k
We have y= 3x+ 1
So, After translating 3 units to x axis the function will become
y' = 3(x - 3) +1
Learn more about Translation here:
https://brainly.com/question/27425612
#SPJ1
The distance (d) in meters a car travels in t seconds is shown in the tables.

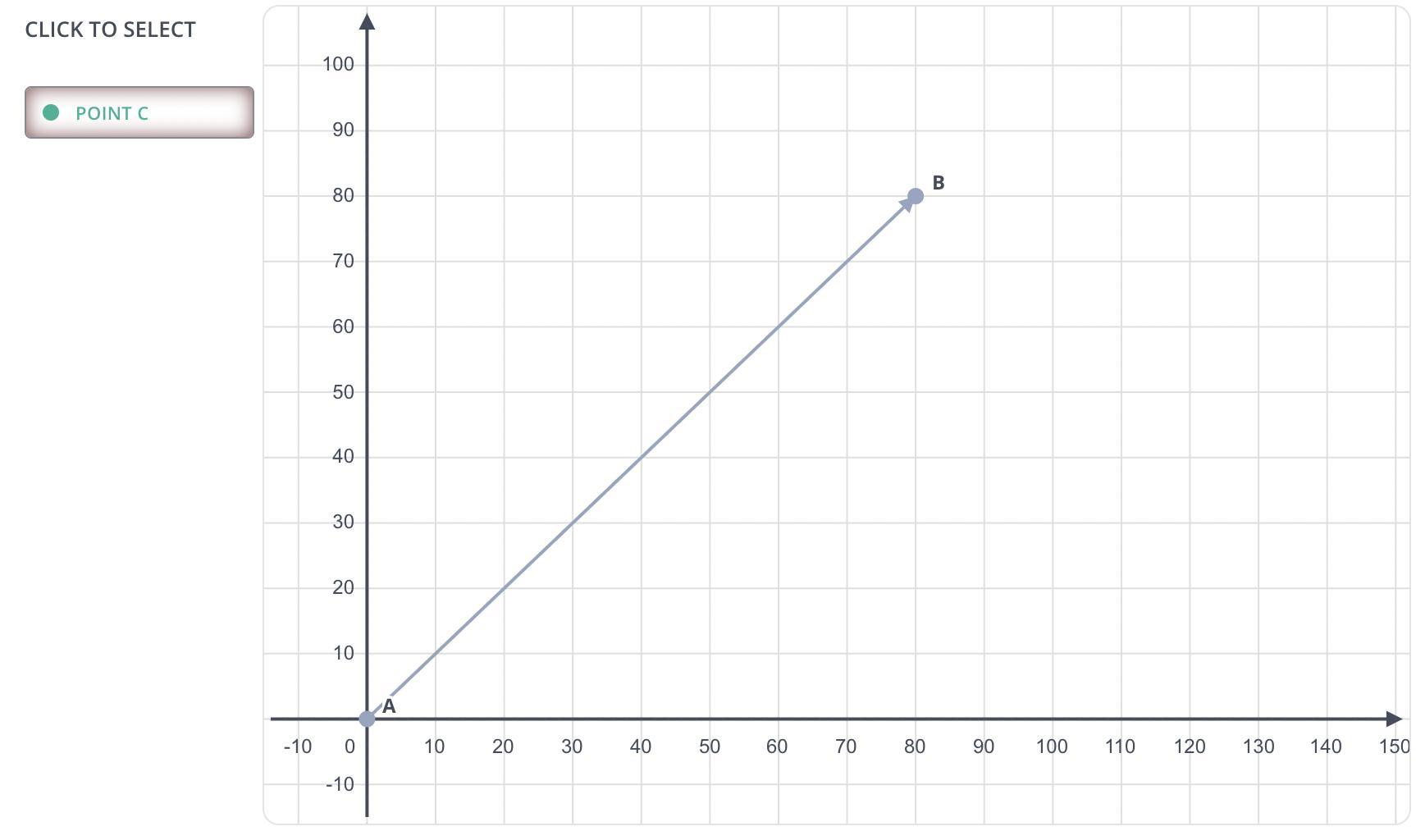
Answers
The proportional relationship between the distance (d) traveled by a car and time (t) is shown in the graph attached below.
What is a proportional relationship?In Mathematics, a proportional relationship is a type of relationship that produces equivalent ratios and it can be modeled or represented by the following mathematical expression:
y = kx
Where:
y represents the distance in miles.x represents the time in hours.k is the constant of proportionality.Next, we would determine the constant of proportionality (k) for the data points on this graph as follows:
Constant of proportionality, k = y/x
Constant of proportionality, k = 10/1 = 10.
In this exercise, we would use an online graphing calculator to plot the proportional relationship between the distance (d) traveled by a car and time (t) as shown in the graph attached below.
Read more on proportional relationship here: brainly.com/question/28350476
#SPJ1

1. 2y +8x =70
2. 2y = 8x- 70
3. y= 8x- 70
What’s the slope and y intercept for these equations?
Answers
Can you give me some hint please
2y = 70 -8x
2y/2 = 70 -8x /2
Y = 35-4x
Y= 4x + 35
The slope here is 4 and the y intercept is 35
2) 2y = 8x -70
2y /2= 8x-70/ 2
Y= 4x -35
The slope here is 4 and the y intercept is -35
3) y= 8x -70
The slope here is 8 and the y intercept is -70
Add -3/4 + 3/4 + 1/4 enter your answer as a simplified mixed number in the box
Answers
Answer:
-3/4+3/4+1/4=0.25
but, you asked for it in a mixed number which would be 1/4
Step-by-step explanation:
subtract f(x)=-5^2+x-2 g(x)=-3^2+3x+9
Answers
Answer: -2x-27
Step-by-step explanation:
Kaleb determined how much money he would spend if he stopped at McDonalds each day after school. His cost can be modeled using c(m)=2.3m+2.50, where m is the number of McGriddle he orders each time. What is the cost that Kaleb would spend at McDonalds if he ordered 3 McGriddles?
Answers
Answer:
The cost that Kaleb would spend at McDonalds if he ordered 3 McGriddles would be 11.50.
Step-by-step explanation:
We know this is the answer because, when solving for c(3), we would get c(3)=2.3(3)+2.50=11.50.
A wiring job requires 4 electricians to work for 6 hours to finish the job.
On the day of the job, one electrician does not report. How long would it
take to complete the same job by the remaining electricians?

Answers
if we are talking about 24hrs. 24/4=6 so 24/3=8 (3 bc there is one less)!
The time and electricians it would take the remaining 3 electricians 8 hours to complete the job if one electrician does not report.
How are number of people to time needed to complete a task related?More people to do a task means less time it will take.
Less people to do a task means more time it will take.
Thus, they are inversely related.
If x men take y time for a work,
We can define a constant as "Manpower" needed for doing that specific work.
Let we define:
Manpower needed for a work = y + y + y + .. + y = Time per man × count of men
Manpower needed for a work = xy
We are given that;
Number of electricians= 4
Number of hours= 6
Now,
We can use the formula:
workers × time = work
where "workers" is the number of electricians, "time" is the number of hours they work, and "work" is the amount of work done.
In this case, we know that 4 electricians can complete the job in 6 hours. So:
4 × 6 = work
work = 24
This means that the total amount of work required to complete the job is 24 "units".
Now, if one electrician doesn't show up, we have only 3 electricians to do the work. Let's call the time it takes for the 3 electricians to complete the job "t".
So we have:
3 × t = 24
Dividing both sides by 3, we get:
t = 8
Therefore, by work and time answer will be 3 electricians and 8 hours.
Learn more about work and time here:
https://brainly.com/question/1063042
#SPJ2
classify the quadrilateral formed at the points: A(-3,1) B(4,2) C(9,-3) and D (2,-4)
tags: geometry homework help need fast
Answers
Answer:
Step-by-step explanation:
To classify the quadrilateral formed by the given points, we need to find the length of each side and the measure of each angle.
Using the distance formula, we can find the length of each side:
AB = sqrt((4 - (-3))^2 + (2 - 1)^2) = sqrt(49 + 1) = sqrt(50)
BC = sqrt((9 - 4)^2 + (-3 - 2)^2) = sqrt(25 + 25) = 5sqrt(2)
CD = sqrt((2 - 9)^2 + (-4 - (-3))^2) = sqrt(49 + 1) = sqrt(50)
DA = sqrt((-3 - 2)^2 + (1 - (-4))^2) = sqrt(25 + 25) = 5
Using the slope formula, we can find the measure of each angle:
Angle ABC: m1 = (2 - 1)/(4 - (-3)) = 1/7
m2 = (-3 - 2)/(9 - 4) = -1/5
tan(ABC) = |(m2 - m1)/(1 + m1m2)| = 3/4
ABC = arctan(3/4) ≈ 36.87°
Angle BCD: m1 = (-3 - 2)/(9 - 4) = -1/5
m2 = (-4 - (-3))/(2 - 9) = 1/7
tan(BCD) = |(m2 - m1)/(1 + m1m2)| = 3/4
BCD = arctan(3/4) ≈ 36.87°
Angle CDA: m1 = (-4 - 1)/(2 - (-3)) = -1
m2 = (1 - (-3))/(-3 - 9) = 1/2
tan(CDA) = |(m2 - m1)/(1 + m1m2)| = 7/5
CDA = arctan(7/5) ≈ 54.46°
Angle DAB: m1 = (1 - (-4))/(4 - (-3)) = 5/7
m2 = (-4 - (-3))/(-3 - 2) = 1/5
tan(DAB) = |(m2 - m1)/(1 + m1m2)| = 3/4
DAB = arctan(3/4) ≈ 36.87°
Therefore, the quadrilateral formed by the given points is a kite, because adjacent sides are congruent and one diagonal bisects the other diagonal at a right angle.
How Do You Know a Solution is a Solution

Answers
Solution in terms of general solution of an equation means the final answer that is gotten for solving the equation
An environmentalist wants to find out the fraction of oil tankers that have spills each month. Step 2 of 2 : Suppose a sample of 333 tankers is drawn. Of these ships, 257 did not have spills. Using the data, construct the 80% confidence interval for the population proportion of oil tankers that have spills each month. Round your answers to three decimal places.
Answers
Answer:
The 80% confidence interval for the population proportion of oil tankers that have spills each month is (0.199, 0.257).
Step-by-step explanation:
In a sample with a number n of people surveyed with a probability of a success of \(\pi\), and a confidence level of \(1-\alpha\), we have the following confidence interval of proportions.
\(\pi \pm z\sqrt{\frac{\pi(1-\pi)}{n}}\)
In which
z is the zscore that has a pvalue of \(1 - \frac{\alpha}{2}\).
Suppose a sample of 333 tankers is drawn. Of these ships, 257 did not have spills.
333 - 257 = 76 have spills.
This means that \(n = 333, \pi = \frac{76}{333} = 0.228\)
80% confidence level
So \(\alpha = 0.2\), z is the value of Z that has a pvalue of \(1 - \frac{0.2}{2} = 0.9\), so \(Z = 1.28\).
The lower limit of this interval is:
\(\pi - z\sqrt{\frac{\pi(1-\pi)}{n}} = 0.228 - 1.28\sqrt{\frac{0.228*0.772}{333}} = 0.199\)
The upper limit of this interval is:
\(\pi + z\sqrt{\frac{\pi(1-\pi)}{n}} = 0.228 + 1.28\sqrt{\frac{0.228*0.772}{333}} = 0.257\)
The 80% confidence interval for the population proportion of oil tankers that have spills each month is (0.199, 0.257).