Answers
The table 4 is a linear function, while the other tables (i.e. tables 1 to 3) are not linear functions
How to determine the function categories?For a function to be a linear function, the function must have a constant rate
This means that as the input value changes, the output values must change at a constant value
Table 1
Here, we have:
x = -2, 0, 2, 4
y = 4, 1, -2, 5
The function increases constantly at input values -2 to 2 by 1.5, but does not increase constantly at input value 4 i.e. an increment of 3.5
So, it is not a linear function
Table 2
Here, we have:
x = -2, -1, 1, 2, 3
y = 17, 13, 5, 1, 3
The function does not increase constantly throughout the domain values
So, it is not a linear function
Table 3
Here, we have:
x = -5, -3, -1, 1, 2
y = -4, -3, -2, 2, 5
The function does not increase constantly throughout the domain values
So, it is not a linear function
Table 4
Here, we have:
x = -5, -3, -1, 0, 2
y = -2, 0, 2, 3, 5
The function increases constantly throughout the domain values by 1
So, it is a linear function
Read more about linear function at
https://brainly.com/question/15602982
#SPJ1
Related Questions
MODELING REAL
LIFE You and a
friend sign up for a
new volunteer project
to increase your
service hours. The
tables show your and
your friend's total
numbers of service
hours after different
numbers of weeks on
the new project. Who
initially has more
service hours? After
(how many weeks do
you and your friend
have the same total
number of service
hours?
Your Service Hours
Weeks, x
4
6
8
10
12
I
3
5
Total hours, y
15
20
25
30
9
35
14
16
Your Friend's Service Hours
Weeks, x
40
Total hours, y
10
14
18
22
(26)
Answers
The number of weeks you and your friend have the same total number of service hours is 2 2/3
How to determine the number of week you and your friend have the same total number of service hours?The given parameters are:
Your friend
Initial = 8
Rate = 2
So, the function is
y = 8 + 2x
You
The points from the table are (4, 15) and (6, 20)
The equation of the function is
y = (y2 - y1)/(x2 - x1) * (x - x1) + y1
So, we have:
y = (20 - 15)/(6 - 2) * (x - 4) + 15
This gives
y = 1.25 * (x - 4) + 15
When the service hours are equal, we have:
1.25 * (x - 4) + 15 = 8 + 2x
Expand
1.25x - 5 + 15 = 8 + 2x
Collect the like terms
2x - 1.25x = -5 + 15 - 8
Evaluate the like terms
0.75x = 2
Divide by 0.75
x = 2 2/3
Hence, the number of weeks you and your friend have the same total number of service hours is 2 2/3
Read more about linear equations at:
https://brainly.com/question/14323743
#SPJ1
The Lcm of 4,9 what is that
Answers
Answer:
36
Step-by-step explanation:
Answer:
36
Step-by-step explanation:
Jackson puts 600.00 into an account to use for school expenses the account earns 2% interest compounded quarterly monthly how much will be in the account after 10 years round your answer to the nearest cent
Answers
By the compound interest formula, you know that
\(undefined\)9x-3-8x=7-x solve for x
Answers
Answer:
x = 5
Step-by-step explanation:
Simplify both sides :
9x - 3 - 8x = 7 - xx - 3 = 7 - xAdd 3 to each side :
x - 3 + 3 = 7 - x + 3x = 10 - xAdd x to each side :
x + x = 10 - x + x2x = 10Divide by 2 on each side :
2x/2 = 10/2x = 5Answer:
x = 5Step-by-step explanation:
9x-3-8x=7-x solve for x
9x - 3 - 8 x = 7 - x
x - 3 = 7 - x
2x = 10
x = 10 : 2
x = 5
-----------------
check
9 * 5 - 3 - 8 * 5 = 7 - 5
2 = 2
the answer is good
Draw the net and calculate the surface area .

Answers
Hello!
surface area
= 2(4 x 2) + 2(12 x 4) + 2(12 x 2)
= 160cm²
The coordinates of the endpoints of BC are B(6,13) and C(11, – 2). Point D is on BC and divides it such that CD:BD is 1:4.
The coordinates of the endpoints of
BC
are B(6,13) and C(11,
–
2). Point D is on
BC
and divides it such that CD:BD is 1:4.
What is the sum of the coordinates of D?
Write your answer as an integer or decimal.
Answers
9514 1404 393
Answer:
11
Step-by-step explanation:
Point D can be found to be ...
D = (4C +B)/5 = (4(11, -2) +(6, 13))/5 = (50, 5)/5 = (10, 1)
The sum of the coordinates of D is ...
10 +1 = 11
Dionne plans to change her yard and would like at least part of the picnic table to be shaded by the umbrella at mid-day.
Determine whether each option below would result in any part of the picnic table being shaded by the umbrella at mid-
day. Explain how you know.
• Option A: Rotate the picnic table 90° clockwise about the point (5, 0).
Option B: Move the umbrella to a location 4 feet to the left and 1 foot down.
• Option C: Move the umbrella to a location 3 feet down and 2 feet to the left.
Enter your answers and explanations in the space provided
Answers
Answer:
Option CStep-by-step explanation:
Refer to attached picture
At midday the shaded area is going to be under the umbrella only, therefore the option moving the table under the umbrella will be the answer.
So the options:
Option A: Rotate the picnic table 90° clockwise about the point (5, 0)
No. The table has dimensions of 4x3, after this rotation the distance between the umbrella and the table will be zero but the table won't go under the umbrella.Option B: Move the umbrella to a location 4 feet to the left and 1 foot down.
No. The movement will bring the umbrella down by one feet and no intersections.Option C: Move the umbrella to a location 3 feet down and 2 feet to the left.
Yes. By moving the umbrella down by 3 feet and to the left by 2 feet, it will cover some part of the table. The lowest point of the umbrella will have the coordinate of (5, 1). So this is the correct option
How do I find GBA and show all the work

Answers
Answer:
Angle ACB = 44°
There are two ways to solve it. Both are right
Solution number 1
From triangle ABC
angle BAC = 180°-(102° +44°) = 36°
Because BG is parallel with AC
Then angle GBA = angle BAC = 34°Another solution
The sum of angles in the shape AGBC = 360°
So angle GBC = 360 - (90 + 90 + 44 + 102) = 34°HELPPP PLEASEEEEE, BRIANLEST WILL BE GIVEN ON CORRECT!

Answers
Step-by-step explanation:
For the first term
\(\Rightarrow \dfrac{6}{5}=\dfrac{5+1}{5}\\\\\Rightarrow 5+\dfrac{1}{5}=5\dfrac{1}{5}\)
(b)
\(\Rightarrow \dfrac{11}{7}=\dfrac{7+4}{7}\\\\\Rightarrow 1+\dfrac{4}{7}=7\dfrac{4}{7}\)
(c)
\(\Rightarrow \dfrac{21}{4}=\dfrac{20+1}{4}\\\\\Rightarrow 5+\dfrac{1}{4}=5\dfrac{1}{4}\)
(d)
\(\Rightarrow \dfrac{32}{7}=\dfrac{28+4}{7}\\\\\Rightarrow 4+\dfrac{4}{7}=4\dfrac{4}{7}\)
(e)
\(\Rightarrow \dfrac{24}{9}=\dfrac{18+6}{9}\\\\\Rightarrow 2+\dfrac{6}{9}=2\dfrac{6}{9}\)
(f)
\(\Rightarrow \dfrac{25}{6}=\dfrac{24+1}{6}\\\\\Rightarrow 4+\dfrac{1}{6}=4\dfrac{1}{6}\)
find the radius and diameter of a circle with a circumference of 51π
Answers
Answer:
Radius = 25.5 units
Diameter = 51 units
Step-by-step explanation:
r = radius of circle
d = Diameter of circle
= \(2r\)
Circumference of circle = \(2\pi r\)
Substitute the provided value of the circumference:
\(51\pi = 2\pi r\)
r is to be isolated and made the subject of the formula:
\(r = \frac{51\pi}{2\pi}\)
\(\pi\) in the numerator and denominator cancel each other outcompletely:
\(r = \frac{51}{2}\)
∴r = radius of circle = 25.5 units
This also means that:
\(d = 2r\)
\(d = 2(25.5)\)
∴d = Diameter of the circle = 51 units
The starting salaries of individuals with an MBA degree are normally distributed with a mean of $40,000 and a standard deviation of $5,000. Refer to Exhibit 6-4. What is the random variable in this experiment? a. Normal distribution b. $40,000 C. Starting salaries d. $5,000
Answers
The random variable in this experiment is the starting salaries of individuals with an MBA degree. Therefore, the answer is option C, "Starting salaries".
The random variable is the quantity that is being measured or observed in a statistical experiment. In this case, the statistical experiment involves measuring the starting salaries of individuals with an MBA degree.
The random variable in this experiment is "starting salaries", as it is the variable of interest that is being measured. The starting salaries are assumed to follow a normal distribution with a mean of $40,000 and a standard deviation of $5,000.
It is important to identify the random variable in a statistical experiment in order to understand what is being measured and to appropriately interpret the results of any statistical analysis. In this case, knowing that the random variable is the starting salaries of individuals with an MBA degree allows us to make inferences about the population of individuals with MBAs and their potential earning potential.
The random variable in this experiment is the starting salaries of individuals with an MBA degree, denoted by X.
X ~ N(40,000, 5,000)
where "~" means "is distributed as", "N" means "normal distribution", 40,000 is the mean of the distribution, and 5,000 is the standard deviation of the distribution.
To learn more about Standard deviation visit;
https://brainly.com/question/23907081
#SPJ4
4.2 The Court lines are 50 mm wide. Court paint covers 7 m² per litre of paint. 4.2.1 Calculate the total length of the centre circle and the two goal semi circles to be repainted. You may use the formula: Total length Circumference of a centre circle + 2 x Circumference of a semicircle =
Answers
The total length of the centre circle and the two goal semi circles to be repainted is 56.22 meters.
How to calculate the Calculate the total length of the centre circle and the two goal semi circles to be repaintedGiven:
Court lines are 50 mm wide.
Court paint covers 7 m² per litre of paint.
The centre circle is a complete circle, so the circumference is given by the formula: Circumference = 2πr
Radius of the entire circle = 9 m / 2 = 4.5 m
Radius of the centre circle = 4.5 m - 0.05 m (converted 50 mm to meters) = 4.45 m
Circumference of the centre circle = 2π(4.45 m) = 27.94 m
Next, let's calculate the circumference of the semicircles:
The semicircles are half circles, so the circumference is given by the formula: Circumference = πr
The radius (r) of the semicircles is the same as the radius of the entire circle, which is 4.5 m.
Circumference of a semicircle = π(4.5 m) = 14.14 m
Total length = Circumference of the centre circle + 2 x Circumference of a semicircle
Total length = 27.94 m + 2(14.14 m)
Total length = 56.22 m
Therefore, the total length of the centre circle and the two goal semi circles to be repainted is 56.22 meters.
Learn more about length at https://brainly.com/question/28322552
#SPJ1
The following steps were used to prove 1. Factor.II. Simplify.III. Use a Pythagorean identity.IV. Use a quotient identity.V. Use a reciprocal identity.In which order were the steps performed?

Answers
Solution
Step 1
Write the trigonometric equation
\(tan^2\theta\text{ - sin}^2\theta\text{ = sin}^4\theta sec^2\theta\)Step 2
Apply the quotient identity
\(\frac{sin^2\theta}{cos^2\theta}\text{ - sin}^2\theta\)Step 3
Factor out the common factor
\(sin^2\theta(\frac{1}{cos^2\theta}-\text{ 1\rparen}\)Step 4
simplify
\(sin^2\theta(\frac{1-cos^2\theta}{cos^2\theta})\)Step 5
Reciprocal identity
\(sin^2\theta(1\text{ - cos}^2\theta)sec^2\theta\)Step 6
Use the Pythagorean identity
\(\begin{gathered} sin^2\theta\text{ + cos}^2\theta\text{ = 1} \\ sin^2\theta\text{ = 1 - cos}^2\theta \\ Hence \\ sin^2\theta(1\text{ - cos}^2\theta)sec^2\theta \\ sin^2\theta\text{ }\times\text{ sin}^2\theta\text{ }\times\text{ sec}^2\theta \end{gathered}\)Step 7
Simplify
\(sin^4\theta sec^2\theta\)Final answer
Option D
IV , I , II , V , III , IV , II
Evaluate P(3, 3)
1
9
6
Answers
How does insurance reduce social burden?
A. Insurance ensures that people don't have to pay high deductibles.
B. Insurance ensures that losses are not passed on to society.
C. Insurance ensures that lenders publicize rates and treat all
customers equally.
D. Insurance ensures that people are treated fairly in hiring and
employment decisions.
Answers
Answer:
c po is the correct aswer
Step-by-step explanation:
correct me if im wrong hope it's help
thanks
Answer:
B. Insurance ensures that losses are not passed on to society
Hope this helps :)
For the expression use a equals three B equals five and C equals six
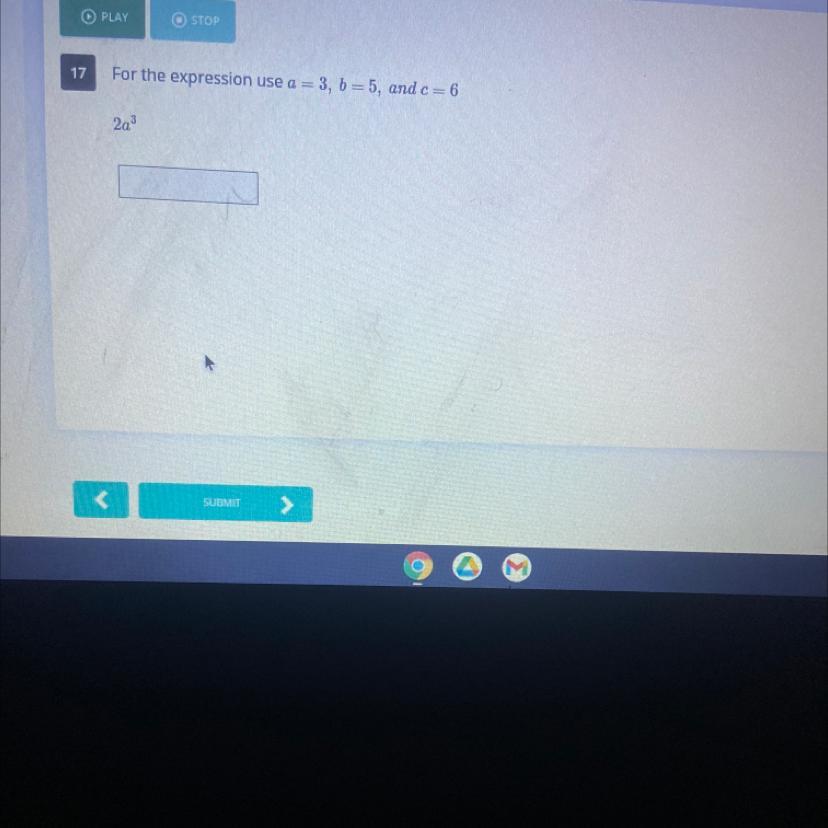
Answers
2a^3 = 2 x 3^3 = 2 x 9
2a^3 = 18
= 2a³
= 2(3)³
= 2×27
= 54
~nightmare 5474~
Desperate Need Of Help

Answers
The domain and range of the graph above in interval notation include the following:
Domain = [-6, 3]
Range = [-3, 3]
What is a domain?In Mathematics and Geometry, a domain refers to the set of all real numbers (x-values) for which a particular function (equation) is defined.
In Mathematics and Geometry, the horizontal portion of any graph is used to represent all domain values and they are both read and written from smaller to larger numerical values, which simply means from the left of any graph to the right.
By critically observing the graph shown in the image attached above, we can reasonably and logically deduce the following domain and range:
Domain = [-6, 3] or -6 ≤ x < 3.
Range = [-3, 3] or -3 < y < 3
Read more on domain here: brainly.com/question/9765637
#SPJ1
Find the state equation of the following system. Which of the following answers is the matrix A in the state equation of * = Ax + Bu? 3x + 2x = f(t) 2ż + 3ż + z = f(t) Selecting the correct answer without being verified by your hand calculations may not get the full credit. Please drop an image of your handwritten work in the corresponding dropbox folder.
Answers
The state equation for the given system is: x' = Ax + Bu where A = [3 2; 0 2] and B = [1; 0].
To find the state equation of the given system, we first need to rewrite it in the matrix form. Let x1 = x and x2 = z, then we have:
x' = [3 2; 0 2]x + [1; 0]f(t)
z' = [2 3; 1 0]z + [0; 1]f(t)
where x' and z' denote the derivatives of x and z with respect to time, respectively. The matrix A in the state equation * = Ax + Bu is given by:
A = [3 2; 0 2]
This is because the state variables x1 and x2 are multiplied by A in the first equation of the state equation. The input matrix B is given by:
B = [1; 0]
This is because only x1 is affected by the input f(t) in the first equation of the state equation.
Therefore, the state equation for the given system is:
x' = Ax + Bu
where A = [3 2; 0 2] and B = [1; 0].
To learn more about matrix refer to:
brainly.com/question/29132693
#SPJ4
Justin biked the same distance every day in the park after school. On Saturday he biked an additional 9 miles, and on Sunday he biked another 12 miles. If Justin biked a total of 86 miles in the 7-day period, how far did he bike each day after school?
Answers
Explanation: 86 - 9 (Saturday) = 77
77 - 12 (Sunday) = 65
65 / 5 (weekdays) = 13
A class is made up of 40% women and has 20 women in it. What is the total number of students in the class?
Answers
Answer:
50
Step-by-step explanation:
Im need help on this question

Answers
Indigo Depot is having a clearance sale of their fall items. A jacket that originally cost $90 before any discount is on sale for 20% off. If the jacket is then put on clearance for an additional 30% off the sale price, what is the final price? Round your answer to the nearest cent, if necessary.
Answers
Answer:
$50.40
Step-by-step explanation:
90 - 20%:
We can use fractions to simplify this percentage:
90 - 2/10 = 90 - 18 = 72.
So before it was put on clearance, it was $72.
After it's put on clearance:
72 - 30% = 72 - 3/10 = 72 - 21.6 = 50.4
So the final price is $50.4.
Find the slope of the line that passes
through

Answers
The slopes of the linear equations are:
a) -1
b) 0
c) undefined, it is a vertical line.
How to find the slopes of the lines?
A general linear equation is written as:
y = a*x + b
Where a is the slope and b is the y-intercept.
If the line passes through two points (x1, y1) and (x2, y2), then the slope is:
a = (y2 - y1)/(x2 - x1)
1) The points are (3, 5) and (2, 6), so the first slope is:
a = (6 - 5)/(2 - 3) =1/-1 = -1
2) The points are (-3, 2) and (7, 2)
Notice that this is a horizontal line of the form y = 2, so the slope is zero.
3) The points are (6, 8) and (6, -2)
This is a vertical line of the form x = 6, so the slope is undefined.
Learn more about linear equations:
https://brainly.com/question/1884491
#SPJ1
\(\large\boldsymbol{\rm{Slope}}\)
\(\bf{Intro}\)
To find the slope of a line, given that it passes through two points, use the slope formula:
\(\bf{m=\dfrac{y_2-y_1}{x_2-x_1}}\)
Substitute the known values and simplify:
\(\bf{m=\dfrac{6-5}{2-3}}\)
\(\bf{m=\dfrac{1}{-1}}\)
\(\bf{m=-1}\) {slope}
\(\rule{250}{1}\)
Substitute the known values and simplify:
\(\bf{m=\dfrac{2-2}{7-(-3)}}\)
\(\bf{m=\dfrac{0}{7+3}}\)
\(\bf{m=\dfrac{0}{10}}\)
\(\bf{m=0}\) {slope}
\(\rule{250}{1}\)
Substitute the known values and simplify:
\(\bf{m=\dfrac{-2-8}{6-6}}\)
\(\bf{m=\dfrac{-10}{0}}\)
\(\bf{m=not\:de fined}\)
✦ Therefore, the slopes are: -1, 0, not defined.
growth mindset is a belief that intelligence can improve through________
my math teacher asking us I can't solve dosen't make sense
Answers
Answer:hard work
Step-by-step explanation:
Remember this from last year Lol
From the top of the 140-foot high tower, an air traffic controller observes an airplane on the runway at an angle of depression of 18°.
18°
140 ft
How far is it from the base of the tower to the airplane? Round your answer to the nearest tenth of a foot.
Answers
Answer:
Step-by-step explanation:
The angle of depression is the downward angle the air traffic controller
looks down from in the tower. It also equals the angle of elevation which is the angle formed by the runway and the line of sight.
With this information you can find the remaining angle:
180 - (90 + 18)
180 - 108 = 72
Let Angle B = 72°
Angle A = 18°
Angle C =90°
We have one side - 140 feet - this is side a - it is across from angle A.
There is a right triangle formed by the runway (side b) the tower, side a, and the line of sight (side c)
Using the law of sines:
sin A/a = sinB/b
sin 18°/a = sin72°/b
.3090/140 = .9510/x
cross multiply and then divide
140 × .9510/.3090
133.14/.3090
430.873 ft
round to a tenth = 430.9 ft
the other one is 27

Answers
Four times Audrey's age plus 7 is Parag's age. Parag is 51. What is Audrey's age?
Answers
Answer:
Audrey is 5 years and 9 months old
Step-by-step explanation:
51 divided by 4 = 12.75
12.75 - 7 = 5.75
75% of 12 is 9
Audrey is 5 years and 9 months old
What is the domain of y = log Subscript 4 Baseline (x + 3)?
Answers
Answer:
All real numbers greater than -3
Step-by-step explanation:
The domain of a log is the baseline is greater than 0.
Set x + 3 greater than zero and solve
x + 3 > 0
x > -3
algebra 2 5.2 decide whether the function is a polynomial function. if it is, write the function in standard form and state the degree,
Answers
Yes, the specified function \(f(x) = \frac{1}{7} x - 4x^2 +4x^4 - 1\) is a Polynomial Functions.
Polynomial Functions:
Polynomial functions are functions that take only non-negative integer powers or positive integer exponents of variables in equations such as quadratic, cubic, etc. For example, 2x+5 is a polynomial with exponent equal to 1.
There are different kinds of polynomial functions based on the degree of the polynomial. The most common types are:
Constant polynomial function: P(x) = a = ax0Zero polynomial function: P(x) = 0; where ai are all zeros, i = 0, 1,…, n.Linear Polynomial function: P(x) = ax + bQuadratic polynomial function: P(x) = ax2+bx+cCubic polynomial function: ax3+bx2+cx+dQuarter polynomial function: ax4+bx3 +cx2 +dx +eAccording to the Question:
The standard form is
\(f(x) = 4x^4 -4x^2 + \frac{1}{7} x - 1\)
The polynomial degree is 4.
Main coefficient is 4.
The given polynomial is
\(f(x) = \frac{1}{7} x - 4x^2 +4x^4 - 1\)
Therefore, The standard form is
\(f(x) = 4x^4 -4x^2 + \frac{1}{7} x - 1\)
The greatest power of the variable is known as the degree.
So the coefficient of the variable with the highest power of degree 4
is called the leading coefficient.
So the leading coefficient is 4.
Learn more about Polynomial Function:
https://brainly.com/question/12976257
#SPJ4
Consider a password which is 4 to 5 characters long, where each character is either an uppercase letter (26 letters) or a digit (0-9). Each password must contain at least one digit.
A: How many possible passwords are there?
B: What is the probability of having a password which is 5 character long and ends in a zero.?
C: What is the probability of having an all digit password?
Answers
A: There are 33,216 possible passwords. The probability of having a 5 character password ending in 0 is 2.7%. The probability of having an all digit password is 0.16%.
The total number of possible passwords can be calculated by multiplying the number of options for each character. There are 26 uppercase letters and 10 digits, so for a 4 character password there are 26 x 26 x 10 x 10 = 67,600 possible combinations. For a 5 character password there are 26 x 26 x 10 x 10 x 10 = 336,960 combinations. Therefore, there are 33,216 possible passwords if the password must be 4-5 characters long and contain at least one digit. The probability of having a password which is 5 characters long and ends in a zero is 2.7%. This is calculated by dividing the number of possible passwords that end in 0 (1,680) by the total number of possible passwords (33,216). The probability of having an all digit password is 0.16%. This is calculated by dividing the number of possible all digit passwords (5,120) by the total number of possible passwords (33,216).
Learn more about probability here
https://brainly.com/question/30034780
#SPJ4
