ANSWER CORRECTLY YOU WILL GET BRAINLY IF YOU ANSWER IN 5 min
Option 2 - Coaster City
Option 1 - Adventureland
$20.00 plus $9.00 per person
$40.00 plus $5.00 per person
Part A: Four members of Monica's family will be going on the trip. Which park is the better option if the family is
on a budget?
Part B: Three of Monica's friends have been invited to join the family of four on their trip. Which park will be the
best option for the group?
Part C. For how many people would the cost be the same for each park?
Write an equation that represents the situation then solve. (Explain/Justify your thinking.)

2527.43 square meters

The formula for calculate the volume of hemisphere is given as:

where"r" is the radius of the hemisphere

Given the following parameters:

• V = 9,202.8 meters cubed.

Substitute the given parameters into the formula to get the radius:

Determine the area of the floor given the radius above:

Hence the area of the floor of the igloo is 2527.43 square meters

Answer:

maybe false

have a great day

true

Explanation:

you can use a2 +b2=c2 to find it

Answer:

1. 0.75

2. 0.25

Step-by-step explanation:

Let's start off with number 1

There is only 2 answers that would make sense.

0.6 and 0.75

But only one is the answer

To find the answer you have to go to the columns that represent the equation

Then you divide

108/144

= 0.75

Now in number 2

You have to place the information in the graph where it corresponds and you get the numbers 24/96

Now divide

24/96

=0.25

Hope this helped :)

Have a good one!

Answer:

Let's denote:

probability that a person paid regular admission P(A)

probability that a person purchased no snack P(B)

probability that a person got discount on admission P(C)

probability that a person purchased snack P(D)

For picture 1

Applying Bayes theorem, we have:

probability that a person paid regular admission, given that person purchased no snack : P(A|B) = P(A ∩ B)/P(B) = (108/240)/(144/240) = 108/144 = 0.75

=> Option D is correct

For picture 2

As shown in picture, we have:

probability that a person got discount on admission and purchased snack:

P(C ∩ D) = 24/240 = 0.1

=> Option C is correct

Hope this helps!

:)

Answer:

$10

Step-by-step explanation:

Since 2 pints is about 1 liter we divide 16 by 2 which is 8 liters.

Now we multiply 1.25 the cost by 8 liters because it's the cost.

= 10

Answer:

y=1.5x-3

Step-by-step explanation:

(0,-3) => x=0, y=-3

(2,0) => x=2, y=0

y=ax+b

-3=a*0+b

0=2*a+b

-3=b

0=2a+b

2a-3=0

2a=3

a=1.5

b=-3

y=1.5x-3

Answer:

\(y = \dfrac{3x}{2} -3\)

Step-by-step explanation:

Before we identify the equation of the line in slope intercept form, we must identify the slope intercept form equation. The slope intercept form equation is y = (m)x + (b) ⇒ m = slope of line; b = y-intercept of line.

To identify the equation of the line shown in slope intercept form, according to the slope intercept form equation, we need to identify the slope of the line and the y-intercept of the line. The slope of a line is the rate of a line, which advances up/down/side-to-side at a constant rate. The y-intercept of a line is the intersection of the line at the y-axis.

There is a specific formula for identifying the slope:

\(\boxed{\text{Slope} = \dfrac{\text{y coordinate of 2nd point - y coordinate of 1st point}}{\text{x coordinate of 2nd point - x coordinate of 1st point}}}\)

Some facts about slope: The slope of a line will also depend on the graph. If the graph ascends upward to somewhere in Quadrant 1 or 2, the slope of the line will be positive. If the graph descends downward to somewhere in Quadrant 3 or 4, the slope will be negative. If the line horizontal and it passes perfectly through the x-axis, the slope of the line is 0. If the slope of the line is vertical, then the slope will be undefined.

Location of plotted points: First point: (0, -3); Second point: (2, 0)

Let us now identify the x and y coordinates of the plotted points:

\(\boxed{\text{y-coordinate of 2nd point = 0; y-coordinate of 1st point = -3}} \\ \boxed{\text{x-coordinate of 2nd point = 2; x-coordinate of 1st point = 0 }}\)

Plug the coordinates into the slope formula to determine the slope:

\(\implies {\text{Slope} = \dfrac{\text{0 - (-3)}}{\text{2 - 0}}} = \dfrac{0 + 3}{2} = \dfrac{3}{2}\)

Plug the slope of the line into the slope intercept form equation:

\(\implies y = (m)x + (b)\)

\(\implies y = \huge\text{(}\dfrac{3}{2} \huge\text{)}x + (b)\)

\(\implies y = \dfrac{3(x)}{2} + b\)

Let us plug any point (that is on the line) for x and y. This will help us find the y-intercept (b). I will plug in the first point because it is my preference.

\(\implies y = \dfrac{3(x)}{2} + b\)

\(\implies -3 = \dfrac{3(0)}{2} + b \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ [\text{First point: (0, -3)} \implies x = 0; y = -3]}\)

\(\implies -3 = 0 + b\)

\(\implies -3 = b\)

Finally, let us substitute the slope of the line and the y-intercept of the line into the slope-intercept form equation. Then, we can simplify both sides of the equation and isolate the y-variable completely on the other side.

\(\implies y = (m)x + (b)\)

\(\implies y = \huge\text{(}\dfrac{3}{2} \huge\text{)}x + (-3)\)

\(\implies y = \dfrac{3x}{2} -3\)

Therefore, the equation of the line in slope intercept form is y = 3x/2 - 3.

Answer:

n = 20

Step-by-step explanation:

in a polygon

interior angle + exterior angle = 180°, so

162° + exterior angle = 180° ( subtract 162° from both sides )

exterior angle = 18°

the sum of the exterior angles of a polygon = 360°

since the polygon is regular then each exterior angle is congruent, then

n = 360° ÷ 18° = 20

Answer:

Step-by-step explanation:

Answer:

x = 9

Step-by-step explanation:

Given equation,

→ 3x - 12 = 15

Now the value of x will be,

→ 3x - 12 = 15

→ 3x = 15 + 12

→ x = 27/3

→ [ x = 9 ]

Hence, the value of x is 9.

Answer:

if CB is 13 and BF is 9 than 13+9=22.So DF must be 22 too. If EF is 7 than 22-7=15 and DE is 15

Answer:

4

Step-by-step explanation:

Alexa landed approximately 11.2 kilometers from the skydiving center. To find out how far from the skydiving center Alexa landed, we need to use some trigonometry.

Let's label the distance that Alexa traveled in the helicopter as "d" and the distance she fell from the helicopter as "x". We can see that the angle between the ground and the line connecting the skydiving center to Alexa's landing spot is 70°

70, degree, since the helicopter ascended at an angle of 20°

20 and the two angles add up to 90°

90.Now we can use the tangent function to find x. Tangent is defined as the opposite side (x) divided by the adjacent side (d), so we have:

\(tan(70^\circ) = \frac{x}{d}\)

Solving for x, we get:

x = d * tan(70°)

We know that d = 3.43.43, point, 4 kilometers, so we can plug that in and calculate:

x = 3.43.43, point, 4 * tan(70°)

x ≈ 11.211.2 kilometers (rounded to one decimal place)

Therefore, Alexa landed approximately 11.2 kilometers from the skydiving center.

To know more about trigonometry,  click here:

brainly.com/question/8958195

#SPJ4

Alexa's friends got her a skydiving lesson for her birthday. Her helicopter took off from the skydiving center, ascending in an angle of 20°

20, degree, and traveled a distance of 3.43.43, point, 4 kilometers before she fell in a straight line perpendicular to the ground.

How far from the skydiving center did Alexa land?

The missing values are derived from the graph as follows:

3 ) 7, 14, 21, 28, 35

4) 3, 7, 10, 14, 17

5) 1, 21, 10, 49, 19

In mathematics, a graph is defined as a graphical representation or diagram that organizes facts or values. The graph's points frequently reflect the relationship between two or more objects.

In order to solve for the above values, the best way is to spot the function that exists in the graph which is given as:

F(y) = 3.5x

In the first table, where x = 2

y= 3.5 *2

= 7

This iteration goes on and on and is consistent for all the values.

In the second table,

Where F(y) is known, for example 10.5, then x is derived as:

10.5 = 3.5x (divide both sides by 3.5)

x = 3

This iteration goes on and on and is consistent for all the values.

In the third table, we simply swap the values back and forth using the function F(y) = 3.5x to derive all values.

Learn more about graphs:

https://brainly.com/question/16608196
#SPJ1

Number of roots in the RHP of the complex plane: 31.2. Number of roots in the RHP of the complex plane: 0

The Routh-Hurwitz stability criterion is a technique for deciding the stability of linear time-invariant systems.

The Routh-Hurwitz criteria are a collection of necessary and sufficient conditions for the stability of a polynomial whose coefficients are real numbers.

It can be used to calculate the location of the roots of a polynomial's characteristic equation. Below are the solutions to the given polynomial equations:

Solution 1: Using Routh-Hurwitz criterion for s⁵ + 3s⁴ + 9s³ + 8s² + 65 + 4= 0:

Routh table is given below: s⁵ = 1 3 4 0 0

s⁴ = 3 8 65 0

s³ = 2.36 16.6 0

s² = 8.9 65 0

s¹ = 68 0

s⁰ = 4

There are three poles in the right half plane (RHP) of the complex plane for the given equation.

Hence, the system is unstable.

Solution 2: Using Routh-Hurwitz criterion for s⁵ + 6s³ + 5s² + 8s + 20=0:

Routh table is given below: 

s⁵ = 1 5

s⁴ = 6 8

s³ = 2 20

s² = 4 -20

s¹ = -10

s⁰ = 20

There are no poles in the RHP of the complex plane for the given equation.

Therefore, the system is stable.

Hence, the answer is:1.1

Note: When the roots of the characteristic equation are located on the imaginary axis, the Routh-Hurwitz criteria fail.

A little change in the equation coefficients leads to no information on stability.

Hence, we cannot conclude the stability of the system.

To know more about polynomial visit:

https://brainly.com/question/11536910

#SPJ11

SOLUTION:

Case: Quadratic Application Word Problem

Given:

Required:

a. How long did it take for Jason to reach his maximum height?

b. What was the highest point that Jason reached?

c. What is Jason’s initial height?

Method:

Step 1: How long did it take for Jason to reach his maximum height?

To calculate this, we find the vertex

From here, the vertex is at (1/2, 484).

Hence it takes 1/2 a second to reach the maximum height

Step 2: What was the highest point that Jason reached?

Also, from the vertex, we get the highest height reached

The maximum height reached was 484 feet

Step 3: What is Jason’s initial height?

The initial height is gotten at the start of the motion, i.e. h(0) = ?

Hence the initial height was 480 feet

Final answer:

A) Time = 1/2 second

B) Maximum Height, H= 484 feet

C) Initial Height, H= 480 feet

The probability of the new engine design being approved given that it is low-energy is 0.2, or 20%.

To find the probability of the new engine design being approved, we need to use the concept of conditional probability.

We can use Bayes' Theorem to calculate this conditional probability:

P(A|H) = P(H|A) x P(A) / P(H)

where P(A|H) is the probability of the engine being approved given that it is high-energy, P(H|A) is the probability of the engine being high-energy given that it is approved, P(A) is the overall probability of the engine being approved (irrespective of energy consumption), and P(H) is the overall probability of the engine being high-energy.

Using the values given in the problem, we can substitute in these probabilities:

P(H|A) = 0.1 (given)

P(A) = P(H)P(A|H) + P(L)P(A|L) = 0.50.1 + 0.50.2 = 0.15

P(H) = 0.5 (given)

Therefore, we can calculate:

P(A|H) = 0.1 x 0.5 / 0.15 = 1/3 = 0.333

This means that the probability of the new engine design being approved given that it is high-energy is 0.333, or approximately one-third. Similarly, we can find the probability of the engine being approved given that it is low-energy:

P(A|L) = P(L|A) x P(A) / P(L)

P(L|A) = 1 - P(H|A) = 0.9 (given)

P(L) = 0.5 (given)

P(A|L) = 0.2 * 0.5 / 0.5 = 0.2

To know more about probability here

https://brainly.com/question/11234923

#SPJ4

To find the probability that x < 7/9, where x and y are randomly chosen from the interval [0,1].

Here are the following steps:
1. Since x and y are chosen independently, we'll focus on x first. The interval for x is [0,1], and we want to find the probability that x lies in the interval [0, 7/9].

2. The interval for x has a length of 7/9 - 0 = 7/9. The interval for y is [0,1] with a length of 1.

3. Since the probabilities are uniform, the probability that x < 7/9 is simply the length of the desired interval (7/9) divided by the total length of the interval for x (1), which is:
P(x < 7/9) = (7/9) / 1 = 7/9.
Since the choice of y doesn't affect this probability, the answer is:

The probability that x < 7/9 when x and y are chosen independently from the interval [0,1] is 7/9.

To learn more about “probability” refer to the https://brainly.com/question/13604758

#SPJ11

The slope of the line shown in the graph is __2/3__

and the y-intercept of the line is __6___

The general linear equation is written as follows:

y = ax + b

Where a is the slope and b is the y-intercept.

On the graph we can see that the y-intercept is y = 6, then we can write the line as:

y = ax + 6

The line also passes through the point (-9, 0), replacing these values in the line we will get:

0 = a*-9 + 6

9a = 6

a = 6/9

a = 2/3

That is the slope.

Learn more about linear equations at:

https://brainly.com/question/1884491

#SPJ1

The graph of y = f(x) can have at most one horizontal asymptote.

A horizontal asymptote is a horizontal line that the curve of the function approaches as x approaches positive or negative infinity. The number of horizontal asymptotes that a function can have depends on the behavior of the function as x approaches infinity and negative infinity.

If the function approaches a single horizontal line as x approaches positive or negative infinity, then that line is the horizontal asymptote. If the function approaches different horizontal lines as x approaches infinity and negative infinity, or if it does not approach any horizontal line, then it does not have a horizontal asymptote.

Therefore, the graph of y = f(x) can have at most one horizontal asymptote, which it approaches as x approaches positive or negative infinity.

Learn more about horizontal asymptote here

https://brainly.com/question/1851758

#SPJ11

Answer:

Yes, it is a quadratic equation.

Step-by-step explanation:

Let's solve it to make it a quadratic equation:

=> \(\frac{x^2+1}{x^2} =5\)

=> x²+1 = 5x²

=> 5x²-x²-1 = 0

=> 4x²-1 = 0

Comparing it with the standard form of quadratic equation i.e.

\(ax^2+bx+c = 0\)

So, we get

a = 4 , b = 0 and c = -1

So, yes. It is a quadratic equation and it is a pure quadratic equation since b is equal to 0.

The correct answer is option C which is the ratio of the numbers is 3:4.

In mathematics, ratios are used to determine the relationship between two numbers it indicates how many times is one number to another number.

Given that:-

As we can see that the numbers are more than 20% so suppose the third number is x so the increased number is 1.2x.

Similarly the second condition the increased number is 1.6x.

So the ratio of the numbers will be:-

Ratio = \(\dfrac{1.2x}{1.6x}\)

Ratio = \(\dfrac{3}{4}\)

Therefore the correct answer is option C which is the ratio of the numbers is 3:4.

To know more about ratios follow

https://brainly.com/question/2328454

#SPJ1

Let y be the number of gallons she need to drive 418 miles

380 miles = 14 gallons

418 miles = x

cross-mutiply

380x =5852

Divide both-side by 380

x = 15.4 gallons

The product of (2x+7) and (x – 5) is option C) 2x^2 - 3x - 35.

What is FOIL method. give a description

FOIL method is a mnemonic technique used to multiply two binomials. The term "FOIL" stands for First, Outer, Inner, Last, and refers to the order in which the terms in each binomial are multiplied.

To use the FOIL method, you start by multiplying the first terms of each binomial, then the outer terms, the inner terms, and finally the last terms. The resulting terms are then combined using addition or subtraction as needed.

Finding the product of given two terms :

The product of (2x+7) and (x – 5) can be found by using the FOIL method.

we multiply the first terms, then the outer terms, then the inner terms, and finally the last terms:

\((2x + 7) \times (x - 5) = 2x^2 - 10x + 7x - 35\)

\((2x + 7) \times (x - 5) = 2x^2 - 3x - 35\)

Therefore, the answer is option C) \(2x^2 - 3x - 35\).

To know more about product visit :

brainly.com/question/22852400

#SPJ1

Answer:

The volume is approximately 13 1/8 feet.

Step-by-step explanation:

Volume of a rectangular prism is calculated by multiplying the width, length, and height together.

3.5w × 2.5l × 1.5h = 13.125

13.125 = 13 1/8. The fraction cannot be reduced any further, so this is its simplest form.

Answer:

There is no image or context

Step-by-step explanation:

Sorry, message me back. I am sure I can asnwer your question.

"if a, then b" means that a is a sufficient condition for b, and that b is a necessary condition for a to be true. The statement is true unless a is true and b is false.

The statement "if a, then b" is known as a conditional statement, which is a type of logical statement that is often used in mathematics and other fields. In this case, the statement means that if statement a is true, then statement b must also be true. If a is false, then the truth value of b is not relevant, as the statement is considered true regardless.

The statement "if a, then b" is often written as "a → b" using logical symbols. The symbol "→" is read as "implies" or "if-then".

For example, consider the statements "If it is raining, then the ground is wet" (a → b). This statement is considered true unless it is raining and the ground is not wet, which is a contradiction. If it is not raining, the truth value of "the ground is wet" is not relevant to the truth of the conditional statement.

In summary, "if a, then b" means that a is a sufficient condition for b, and that b is a necessary condition for a to be true. The statement is true unless a is true and b is false.

To know more about Statements:

https://brainly.com/question/30244655

#SPJ11

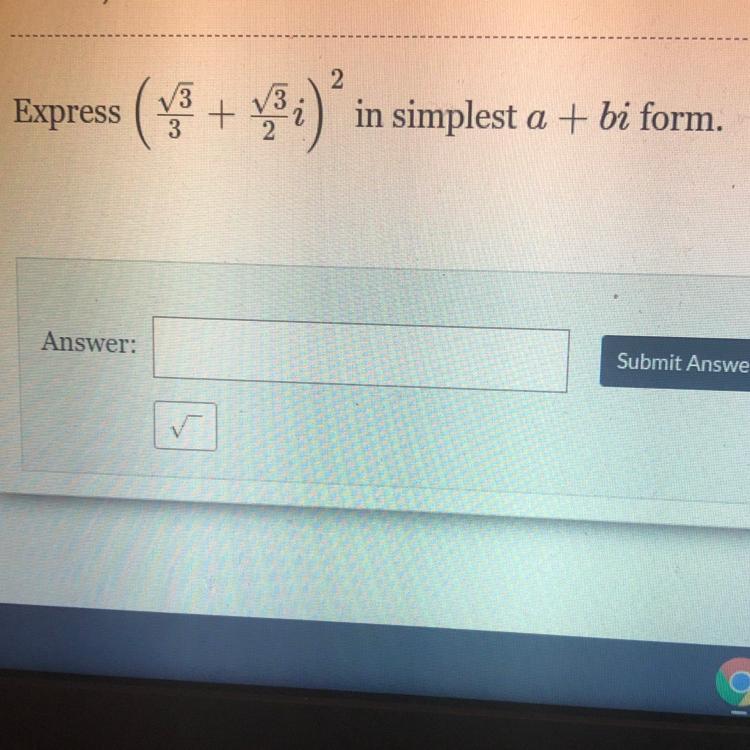
Answer:

Sorry I cant help

Step-by-step explanation:

Answer:

Step-by-step explanation:

\((\frac{\sqrt{3}}{3} +\frac{\sqrt{3}}{2} i)^2\\=\frac{3}{9} +\frac{3}{4} i^2+2 *\frac{\sqrt{3}}{3} *\frac{\sqrt{3}}{2} i\\=\frac{1}{3} -\frac{3}{4} +i\\=\frac{4-9}{12} +i\\=-\frac{5}{12} +i\\\)

[i²=-1]

which is of the form a+bi

where a=-5/12,b=1

As per the problem statement, there is a linear relation,  between de whole earnings of Jada,  and her working time.

Solution:

y = 240 + 6×t

A Linear relation  is of the form:

y = ax + b

If we call total earnings´Jada "y",  and "t" the whole quantity of worked hours per week,  we get:

a fixed amount working 40 hours      12×40 = 480 $

and the quantity over 40 hours as   ( t - 40 ) × 6.

Then  y = fixed quantity + overtime

y = 480 + ( t - 40 ) × 6       reordering this expression

y = 480 + 6×t - 240

y = 240 + 6×t

Just for checking,  if this equation satisfies, the conditions of the problem

if t = 40 h    that means she did´nt do any overtime,

she earns    y = 240 + 6×(40)   ⇒  y = 480 $

if t = 50 h  meaning 10 hours of overtime, she earns:

y = 240 + (50)×6   ⇒  y = 540 $

Related Links : https://brainly.com/question/21835898

The equation of the line passing through  (-4,-6), (5,-6) will be y = -6

In the given question, it is stated that the line passes through points  (-4,-6), and (5,-6). We need to find out an equation of the line that satisfies the given condition.

Firstly, we will need to find out the slope of the line. We can find the slope by using the point-slope form which is represented by:

=> \(m = \frac{y_{2}-y_{1} }{x_{2} - x_{1} }\)

Putting values (x₁, y₁) =  (-4,-6) and (x₂, y₂) = (5,-6) we get:

=> \(m = \frac{-6+ 6 }{5+ 4 }\)

=> m = 0

We get slope m = 0. Now, putting the value of slope into the point-slope form and taking (x₁, y₁) =  (-4,-6), we get values:

=> y - y₁ = m(x - x₁)

=> y + 6 = 0(x + 4)

=> y = -6

Hence, we get the equation of line y = -6

To know more about the Point-slope form, Click here:

https://brainly.com/question/11317454

#SPJ9