(ANSWER ASAP PLZZ) WILL MARK BRAINEST IF CORRECT)Jason and 4 friends went bowling. Three friends rented shoes for $2 each. The total cost to rent the shoes and the lane fees was $42. What was the cost of the lane fees for each person?
Answers
Answer: 30/4
Step-by-step explanation:
Related Questions
Using the 100/50/20 Rule for daily fluid requirements (DFR). Calculate the following questions, do not round the patient's weight but round all final answers to a whole number. 1-10 kg = 100ml/kg/day 11-20 kg = 50ml/kg/day (+ 1000 mL/day for 1* 10kg) Over 20kg = 20mL/kg/day (1500 mL/day for 1s 20kg) 18. An infant weighs 11 pounds. What is the required amount of fluid per day in ml? I 19. A child weighs 31 lbs and 8 ozs. What is the required amount of fluid per day in ml? If no oral fluids are consumed, what is the hourly IV flow rate to maintain proper hydration?
Answers
18. An infant weighs 11 pounds which is equivalent to 4.98 kg. Using the 100/50/20 Rule, the required amount of fluid per day for an infant between 11-20 kg is 50 ml/kg/day. So, the required amount of fluid per day in ml is 4.98 kg x 50 ml/kg/day = 249 ml/day.
19. A child weighs 31lbs and 8 ozs which is equivalent to 14.21 kg. Using the 100/50/24 Rule, the required amount of fluid per day for a child over 20 kg is 20 ml/kg/day. So, the required amount of fluid per day in ml is 14.21 kg x 20 ml/kg/day = 284.2 ml/day.
If no oral fluids are consumed, the hourly IV flow rate to maintain proper hydration would be: 284.2 ml/day / 24 hours/day = 11.8 ml/hour.
Daily Fluid Requirements (DFR)The question is about fluid requirements for infants and children, and it is using the 100/50/20 Rule for Daily Fluid Requirements (DFR) to calculate the required amount of fluid per day for different weight ranges. The 100/50/20 Rule is a guideline used to determine the appropriate amount of fluid that infants and children should receive on a daily basis based on their weight. The rule states that for infants and children up to 10 kg, the recommended fluid intake is 100 ml/kg/day, for those between 11-20 kg it is 50 ml/kg/day, and for those over 20 kg it is 20 ml/kg/day.
The question also asking about the hourly IV flow rate to maintain proper hydration if no oral fluids are consumed.
This subject is part of pediatrics, more specifically in the field of fluid and electrolyte balance and management.
Learn more about Daily Fluid Requirements (DFR) here:
https://brainly.com/question/28334028
#SPJ4
503.782 rounded to the nearest tenth
Answers
Answer: 503.8
Step-by-step explanation:
since 5 - 9 goes up and 1 - 4 goes down you round the 7 to the 8 and make the 7 an 8 and make all the other numbers a 0 since you rounded up to get 503.80 or just 503.8
The area of Gateway National Recreation Area is about twenty-six thousand, six hundred six and sixty-three hundredths. Which shows this number in standard form?
Answers
Answer:
B, 26,606.63
Step-by-step explanation:
You have round tables each seating 6 people. As your guests sit at the table, how many degrees must you rotate to look from the guest to their left to the guest to their right? (Hint: The interior angles of regular polygon measure ((n - 2) x 180) / n where n is the number of sides.)
Answers
To look from the guest to their left to the guest to their right at a round table seating 6 people, you need to rotate by 60 degrees.
For a regular polygon with n sides, the sum of its interior angles is given by ((n - 2) × 180) degrees. In the case of a round table seating 6 people, the table can be considered as a hexagon, which has 6 sides. Using the formula, we can calculate the sum of the interior angles:
((6 - 2) × 180) / 6 = (4 × 180) / 6 = 720 / 6 = 120 degrees
Since the table forms a complete circle, the sum of the interior angles is divided equally among the guests. Therefore, each guest sits at an angle of 120 degrees. To look from the guest to their left to the guest to their right, you need to rotate by the angle between adjacent guests, which is half of the angle they sit at:
120 / 2 = 60 degrees
Thus, to look from the guest to their left to the guest to their right at a round table seating 6 people, you need to rotate by 60 degrees.
Learn more about angle here:
https://brainly.com/question/31818999
#SPJ11
∆ABC was transformed according to the rule (x, y) → (−x, y) to create ∆A'B'C'. What transformation justifies the relationship between the triangles?
Answers
A 90° rotation around the origin characterised the transition.
What is the transformational rule?A logical principle that specifies the circumstances in which one assertion can be legitimately inferred from one or more other statements, particularly in codified languages.
What transformation does the rule x y → − x − y?(x, y)(x, y) is the formula for a reflection over the x-axis.
Triangle ABC was changed utilizing the (x, y) rule (–y, x). The triangles' vertices are displayed. A (–1, 1) B (1, 1) C (1, 4) (1, 4) A' (–1, –1) (–1, –1) B' (–1, 1) C' (–4, 1) (–4, 1) Which phrase best sums up the change? A 90° rotation around the origin characterised the transition. A 180° rotation of the origin occurred during the transformation. The transformation was a 270° rotation about the origin. The transformation was a 360° rotation about the origin.
To know more about Transformed visit:
brainly.com/question/28874044
#SPJ1
Answer: A reflection over the y-axis justifies ∆ABC ≅ ∆A'B'C'.
Step-by-step explanation: Took the test, no thanks neeeded :)
The surface area of sphere T is 452.16 units squared. The surface area of sphere X is 1,808.64 units squared. How many times larger is the radius of sphere X than the radius of sphere T
Answers
Answer:
Step-by-step explanation:
Comment
The surface area for a sphere is 4 pi * r^2
Givens
Surface Area X = 1808.64
Surface Area T = 452.16
Solution
Sphere X
Surface Area = 4 pi r^2
Surface Area X = 4 * 3.14
1808.64 = 12.56 * r^2 Divide both sides by 12.56
1808.64/12.56 = 12.56 r^2/12.56
r^2 = 144 Take the square root of both sides
√^2 = √144
r = 12
Sphere T
Surface Area = 4 pi r^2
452.16 = 12.56 r^2 Divide by 12.56
452.16 / 12.56 = 12.56 r^2/12.56
r^2 = 36 Take √ of both sides
√r^2 = √36
r = 6
Conclusion
radius x: radius T :: 12/6
radius x: radius T :: 2/1
Find the area of the sector interms of pi.12210°Area = [?]
![Find the area of the sector interms of pi.12210Area = [?]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/1KIK9vbxESZiPrtIV7F0E0MEDGM4IepG.jpeg)
Answers
section = 210/360 = 7/12
Area = pi*r^2
Area = 12^2*pi
Area = 144*pi
Area = 7/12*144*pi
Area = 1008/12*pi
Area = 84~pi this is the result
Question 5 of 10
1.8"
22.8"
15.8"
Which of the following volume measurements is the best estimate for the
figure above? Round each measurement to the nearest whole number to get
your estimate.
OA. 690 in ³
B 330 in ³

Answers
The estimated volume of the given cuboid is 736 inch³
The volume of a Cuboid:In geometry, a cuboid is a three-dimensional figure or geometrical shape that has 6 faces, 12 edges, and 8 vertices. The space occupied by the cuboid is known as the Volume of the cuboid.
The dimensions of the cuboid are Length, Width, and Height. The formula for the volume of the cuboid is given by
Volume of cuboid = Length × Width × Height
Here we have
Measurements cuboid are
Length = 22.8 inches
On rounding to a whole number, Lenght = 23 inches
Width = 1.8 inches
On rounding to a whole number, Width = 2 inches
Height = 15.8 inches
On rounding to a whole number, height = 16 inches
As we know
The volume of a cuboid = Length × Width × Height
= 23 inch × 2 inch × 16 inch
= 736 inch³
Therefore,
The estimated volume of the given cuboid is 736 inch³
Learn more about Volume of a Cuboid
https://brainly.com/question/29568631
#SPJ1
The radius of a circle is 3 inches. What is the length of a 45° arc?
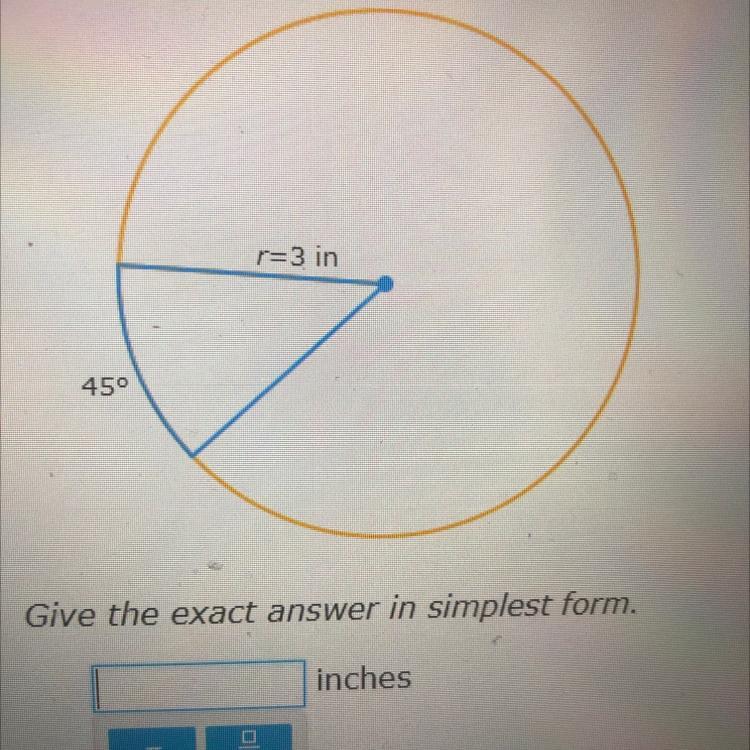
Answers
Answer:
\(\frac{3\pi}{4}\:\text{inches}\)
Step-by-step explanation:
The length of an arc is a part of the circle's circumference.
The circumference of a circle is equal to \(2\pi r\), where \(r\) is the radius of the circle. Therefore, the circumference of the circle is \(2\pi(3)=6\pi\).
Since there are 360 degrees in a circle, the length of a 45 degree arc is equal to \(\frac{45}{360}\) of the circumference.
Thus, the length of the arc is equal to \(\frac{45}{360}\cdot6\pi =\boxed{\frac{3\pi}{4}\:\text{inches}}\).
Is the relation a function?
(9,-8) (12, 7) (1, 13) (-9, 3) (4, 0)
Yes
No
No answer text provided.
O No answer text provided.

Answers
The equation y = 70.5 + $ 19.5 sin [pi/6 (t - 4)] models the average monthly temperature for Phoenix, Arizona, in degrees Fahrenheit. In this equation, t denotes the number of months, with t " 1 representing January. What is the average monthly temperature for July?
Answers
The average monthly temperature for July is $90 degrees Fahrenheit.
To calculate the average monthly temperature for July, we need to determine the value of y when t corresponds to July.
In the given equation, y = 70.5 + $19.5sin[(π/6)(t - 4)], t represents the number of months, with t = 1 representing January.
Since July is the seventh month of the year, we can substitute t = 7 into the equation to find the average monthly temperature for July:
y = 70.5 + $19.5sin[(π/6)(7 - 4)]
= 70.5 + $19.5sin[(π/6)(3)]
= 70.5 + $19.5sin[π/2]
= 70.5 + $19.5(1)
= 70.5 + $19.5
= 90
Hence the temperature in july is 90 degree farenheit.
Learn more about temperature here, https://brainly.com/question/26866637
#SPJ11
8. An employee at the recreation center earns $84.00 for working 7 hours. At
this hourly rate, what should the employee earn for 40-hour work week?
A. $12.00
B. $ 480,00
C. $ 280,00
D. $ 21,00
Answers
Answer:
B $480.00
Step-by-step explanation:
7. Malik deposited
$1,050 in a savings
account, and it earned
$241.50 in simple
interest after four years.
Find the interest rate on
Malik's savings account.
I got 5.75 on a website but I need to show my work SOMEONE PLEASE HELP ME!
Answers
I've been stuck on this for a bit, and I'm still figuring this out in the process. a little help?

Answers
Steps to solve:
4x + 1/3y^2 when x = 2 and y = 3
~Substitute
4(2) + 1/3(3)^2
~Simplify
8 + 1/3(9)
~Simplify
8 + 3
~Add
11
Best of Luck!
(-3) to the sixth power in exponential form
Answers
Answer:
Step-by-step explanation:
A negative number raised to an even exponent gives a positive result so it is the same as 3 raised to 6. That is 3 x 3 x 3 x 3 x 3 x 3 = 729
The (-3) to the sixth power, (-3)⁶, is equal to 729.
To express (-3) to the sixth power in exponential form, we write it as (-3)⁶.
Now, let's calculate (-3)⁶ properly:
(-3)⁶ = (-3) * (-3) * (-3) * (-3) * (-3) * (-3)
Multiplying -3 by itself six times:
(-3) * (-3) * (-3) * (-3) * (-3) * (-3) = 729
Therefore, (-3) to the sixth power, (-3)⁶, is equal to 729.
By raising -3 to the power of 6, we obtain the result of 729.
To know more about power:
https://brainly.com/question/15149964
#SPJ6
Please help! 20 points given

Answers
Answer: Its 5,2,-5,-4/3 i think but js,,,,
Step-by-step explanation:Bc you have to look at da x cordinate fist than da y an find them
Answer:
1, -3, -1, 4
Step-by-step explanation:
The domain of a function is all the possible inputs (or x-values) for a function.
Let's write out the points so we can better analyze the x and y values:
(1,2)
(-3,-4)
(-1,-5)
(4,-4)
If we look at the x-values in each point (the first number in each point is the x-value of the point), we will be able to find the numbers in the function's domain.
Please answer the questions in the photo ( will mark brainliest )

Answers
The reason for the required step using property of equality are as follow:
1. Subtraction property of equality.
2. Subtraction property of equality.
3. Addition property of equality.
As given in the question,
The reason for the required step using property of equality are as follow:
1. 3x + 3 = 5 + x
3x - x + 3 = 5
2x + 3 = 5
Here
Subtraction property of equality is applied.
If x, y, and z are real numbers and x = y
then
x - z = y - z
2. 2x + 3 = 5
2x = 5-3
2x = 2
Here Subtraction property of equality is applied.
If a, b, and c are real numbers and a = b, then
a - c = b - c
3. -x - 1 = 3
-x = 3 + 1
-x = 4
Here Addition property of equality is applied.
If x, y and z are real numbers and x = y, then
x + z = y + z
Therefore, the reason for the required step using property of equality are as follow:
1. Subtraction property of equality.
2. Subtraction property of equality.
3. Addition property of equality.
Learn more about property of equality here
brainly.com/question/13130806
#SPJ1
Find the volume of the region e that lies between the paraboloid z − 24 2 x 2 2 y 2 and the cone z − 2sx 2 1 y 2
Answers
The volume of region E is approximately 1932.83 cubic units.
We have,
To find the volume of the region E between the paraboloid and cone, we need to set up a triple integral in cylindrical coordinates.
First, let's find the intersection between the paraboloid and cone:
24 - x² - y² = 2√(x² + y²)
(24 - x² - y²)² = 4(x² + y²)
576 - 48(x² + y²) + (x² + y²)² = 4(x² + y²)
(x² + y²)² - 52(x² + y²) + 144 = 0
And,
r² = x² + y²
we can solve for r:
r² = (52 ± √2084)/2
r² = 26 ± 2√521
Since the cone extends farther out than the paraboloid, we'll use the larger value of r:
r = √(26 + 2√521)
To set up the triple integral, we need to express z as a function of r and θ. We can do this by setting the equations for the paraboloid and cone equal to each other and solving for z:
24 - r² = 2r
z = 2r - (24 - r²)
So the volume of region E is given by:
∫∫∫E dz dy dx = ∫0^{2π} ∫0^r ∫(2r - (24 - r²))^(24 - r² - 2r) r dz dr dθ
Evaluating this integral gives the volume of the region E.
To find the limits of integration, we need to set the two equations equal to each other:
24 - x² - y² = 2√(x² + y²)
Squaring both sides, we get:
576 - 48x² + x⁴ - 48y² + y⁴ - 96x²y² = 4x² + 4y²
Simplifying, we get:
x⁴ - 44x² + y⁴ - 44y² + 96x²y² - 572 = 0
This equation is difficult to solve algebraically, so we will solve it numerically using a graphing calculator or a computer algebra system.
By plotting the equation on a graph, we can see that the limits of integration for x and y are approximately -5.5 to 5.5.
Therefore, the integral becomes:
∭E dV = ∫∫∫ E dz dy dx = ∫(-5.5 to 5.5) ∫ (-5.5 to 5.5) ∫(2√(x² + y²) to 24 - x² - y²) dz dy dx
Evaluating the integral gives:
∭E dV = ∫(-5.5 to 5.5) ∫ (-5.5 to 5.5) ∫ (2√(x² + y²) to 24 - x² - y²) dz dy dx
= ∫ (-5.5 to 5.5) ∫ (-5.5 to 5.5) (24 - x² - y² - 2√(x² + y²)) dy dx
= ∫ (-5.5 to 5.5) (∫ (-5.5 to 5.5 (24 - x² - y² - 2√(x² + y²)) dx) dy
= ∫( -5.5 to 5.5 (432 - 33x² - 11x⁴/12 - 33y² - 11y⁴/12 - 256√(x² + y²) +
64(x² + y²)^(3/2)/3) dy
= 24576/5 - 478/15π - 480√2 + 832/3 ln (1 + √2)
= 1932.83 cubic units
Therefore,
The volume of region E is approximately 1932.83 cubic units.
Learn more about paraboloid here:
https://brainly.com/question/31631123
#SPJ1

A survey of 49 randomly selected iPhone owners showed that the purchase price has a mean of $680 with a sample standard deviation of $21. (Use z Distribution Table.) A) Compute the standard error of the sample mean. (Round your answer to the nearest whole number.) B) Compute the 99% confidence interval for the mean. (Use t Distribution Table.) (Round your answers to 3 decimal places.) C) To be 99% confident, how large a sample is needed to estimate the population mean within $7? (Round up your answer to the next whole number.)
Answers
Standard error of the sample mean ≈ $3. The 99% confidence interval for the mean is approximately $671.966 to $688.034. A sample size of 59.669 is needed to estimate the population mean within $7 with 99% confidence.
A) To compute the standard error of the sample mean, we use the formula: standard error = sample standard deviation / √(sample size).
Standard error = $21 / √49 ≈ $3
B) To compute the 99% confidence interval for the mean, we use the t-distribution. The formula for the confidence interval is:
Confidence interval = sample mean ± (t-value * standard error)
First, we need to find the t-value for a 99% confidence level with (n-1) degrees of freedom. Since the sample size is 49, the degrees of freedom is 49-1=48. Using the t Distribution Table, the t-value for a 99% confidence level and 48 degrees of freedom is approximately 2.678.
Confidence interval = $680 ± (2.678 * $3)
Lower limit = $680 - (2.678 * $3)
≈ $680 - $8.034
≈ $671.966
Upper limit = $680 + (2.678 * $3)
≈ $680 + $8.034
≈ $688.034
Therefore, the 99% confidence interval for the mean is approximately $671.966 to $688.034.
C) To determine the sample size needed to estimate the population mean within $7 and be 99% confident, we use the formula: sample size = (z-value * sample standard deviation / margin of error)².
The z-value for a 99% confidence level is approximately 2.576 (obtained from the z Distribution Table).
Margin of error = $7.
Sample size = (2.576 * $21 / $7)²
= (2.576 * 3)²
= 7.728²
≈ 59.669
LEARN MORE ABOUT Standard error here: brainly.com/question/32854773
#SPJ11
A Bunch of Systems
Solve each system of equations without graphing and show your reasoning. Then, check
your solutions.
2x + 3y = 7
-2x + 4y = 14
Answers
Answer:
(- 1, 3 )
Step-by-step explanation:
2x + 3y = 7 → (1)
- 2x + 4y = 14 → (2)
add (1) and (2) term by term to eliminate x
(2x - 2x) + (3y + 4y) = (7 + 14)
0 + 7y = 21
7y = 21 ( divide both sides by 7 )
y = 3
substitute y = 3 into either of the 2 equations and solve for x
substituting into (1)
2x + 3(3) = 7
2x + 9 = 7 ( subtract 9 from both sides )
2x = - 2 ( divide both sides by 2 )
x = - 1
As a check
substitute the values of x and y into the left side of both equations and if equal to the right side in both equations then the values of x and y are true.
(1) 2(- 1) + 3(3) = - 2 + 9 = 7 ← true
(2) - 2(- 1) + 4(3) = 2 + 12 = 14 ← true
then (- 1, 3 ) is the solution to the system
Answer:(- 1, 3 )
Step-by-step explanation:
A very good poker player is expected to earn $1 per hand in $100/$200 Texas poker Hold'em. The standard deviation is approximately $31.
a) What is the probability of a very good poker player earns a profit(more than $0) after playing 40 hands in $100/$200 Texas Hold'em?
b) What proportion of the time can a very good poker player expect to earn at least $500 after playing 100 hands in $100/$200 Texas Hold'em.
c) Suppose that twenty hands are played per hour. What is the probability that a very good poker player earns a profit during a 14 hour session?
Answers
a) The probability of a very good poker player earning a profit (more than $0) after playing 40 hands in $100/$200 Texas Hold'em can be calculated using the normal distribution and the given mean ($1) and standard deviation ($31). b) The proportion of the time a very good poker player can expect to earn at least $500 after playing 100 hands in $100/$200 Texas Hold'em can be calculated using the normal distribution and the given mean ($1) and standard deviation ($31).
To compute these probabilities, we need to make some assumptions and use probability distribution calculations based on the given information.
a) To determine the probability of a profit after playing 40 hands, we can use the concept of the normal distribution. We need to calculate the z-score using the formula: z = (x - μ) / σ, where x is the desired profit, μ is the expected profit per hand, and σ is the standard deviation. In this case, x = $0, μ = $1, and σ = $31.
Once we have the z-score, we can use a standard normal distribution table or calculator to find the corresponding probability.
b) Similarly, to find the proportion of the time a player can expect to earn at least $500 after playing 100 hands, we need to calculate the z-score for x = $500, using the same formula as in part (a). Then, we can use the standard normal distribution table or calculator to find the corresponding proportion.
c) To determine the probability of earning a profit during a 14-hour session, we need to calculate the number of hands played, which is 20 hands per hour multiplied by 14 hours. Let's denote it as N. Then, we can calculate the mean profit for the 14-hour session by multiplying the expected profit per hand ($1) by N.
The standard deviation for the session can be calculated by multiplying the standard deviation per hand ($31) by the square root of N. Finally, we can use the normal distribution and the same z-score calculation as in part (a) to find the probability.
Please note that the above calculations assume that the profits from each hand are independent and follow a normal distribution. Real poker outcomes may deviate from these assumptions.
To know more about probability refer here:
https://brainly.com/question/31828911#
#SPJ11
Clark spent a total of $38 on a pair of shoes and a new jacket. The shoes cost $6 more than the jacket. Write a system of equations to find the cost of the shoes x and the cost of the jacket y. Then find the cost of the shoes.
Answers
Equation 1: x + y = $38
Equation 2: x = y + $6
Replace x in the first equation with the second equation :
y + 6 + y = 38
Simplify:
2y + 6 = 38
Subtract 6 from both sides:
2y = 32
Divide both sides by 2:
Y = 16
Now you know y, the cost of the jacket is $16
The shoes were $6 more so 15 + 6 = $22
Jacket cost $16
Shoes cost $22
Shoes: $22
Jacket: $16
Divide 38 by 2, which is 19
take away half of 6, which is 3.
Take 3 from 19, resulting in 16 which is your jacket
Add 3 to 19, resulting in 22 which are your shoes
A newly-hatched catfish typically weighs 0. 30gram. During the first 6 weeks of life, its growth rate is approximately exponential, increasing about 10% each day. What is the growth rate, k?.
Answers
During the first six weeks of life, a freshly hatched catfish weighs 0.30gram, hence the growth rate, k, is 4.33g.
what is growth rate ?The term "growth" describes an increase in the size and mass of an organ or a body. Cell division and an increase in intracellular material are the usual mechanisms. Development is the maturing of an organism's physiology and functionality.
calculation
The equation is as follows: A = C(1+r)x (I substituted x for t due to the math editor's restrictions). Remember that x represents time in days here.
The rate of increase, r, is as follows: 10% = 10/100 = 0.1
A is the final weight after x (or t) days, while C is the starting weight.
The equation provides:
A = 0.3 (1 + 0.1)ˣ = 0.3(1.1)ˣ
7 days, 7 weeks, and 4 days make up x, which is 28 days.
Compute:
A = (0.3g)(1.1)\(^{28}\)
A = 4.33g
During the first six weeks of life, a freshly hatched catfish weighs 0.30gram, hence the growth rate, k, is 4.33g.
To know more about growth rate visit :-
https://brainly.com/question/14263843
#SPJ4
A, B, C, D, E and F are points on a circle. Put crosses on the ends of the line that is a diameter of the circle.

Answers
Answer:
The line from point F to point C shows the diameter.
Step-by-step explanation:
The diameter of a circle is the measure from one side of it to the other, but it must run directly through the middle. The only line the runs directly through the middle of this circle is line FC, the line that goes from point F to point C.
I hope this helps!
8. Paul can type 4 pages in 15 minutes. How many total pages can he type in one hour? In five hours?
Answers
Paul can type 16 pages in one hour and 80 pages in five hours.
How many pages can Paul type in one hour and five hours if he can type 4 pages in 15 minutes? Paul can type 16 pages in one hour (60 minutes / 15 minutes = 4 sets of 4 pages). In five hours, he can type 80 pages (16 pages/hour x 5 hours).The given information is that Paul can type 4 pages in 15 minutes. We can calculate how many pages he can type in one hour by dividing 60 minutes (one hour) by 15 minutes (time to type 4 pages), which gives us 4 sets of 4 pages. Therefore, Paul can type 16 pages in one hour. To calculate how many pages he can type in five hours, we simply multiply the pages he can type in one hour (16) by the number of hours (5), giving us a total of 80 pages.
Learn more about Paul
brainly.com/question/17450953
#SPJ11
A bar of cast iron 18.125" long has been tapered from a diameter of 0.983" to a diameter of 2.74". What is the difference in diameter between the two ends?
Answers
Answer:
The difference in diameter between the two ends is 1.757''
Step-by-step explanation:
Given;
length of a bar of cast iron, L = 18.125"
initial diameter of the bar, d₁ = 0.983"
final diameter of the bar, d₂ = 2.74"
The difference in diameter between the two ends of the bar is calculated as;
difference in diameter = d₂ - d₁
difference in diameter = 2.74" - 0.983"
difference in diameter = 1.757''
Therefore, the difference in diameter between the two ends is 1.757''
Brandon has 23 3/5 yards of upholstery fabric and 18 1/2 yards of drapery fabric into 2 5/6 yard pieces. How many more drapery pieces than upholstery pieces does Brandon have?
Answers
The number of more drapery pieces than upholstery pieces does Brandon have is 2.03 pieces
FractionUpholstery fabric = 23 3/5 yardsDrapery fabric = 18 1/2 yardEach fabric piece = 2 5/6 yardsNumber of pieces of upholstery fabric = 23 3/5 ÷ 2 5/6
= 118/5 ÷ 17/6
= 118/5 × 6/17
= 708 / 85
= 8 28/85
Number of pieces of drapery fabric = 18 1/2 ÷ 2 5/6
= 37/2 ÷ 17/6
= 37/2 × 6/17
= 222/34
= 6 18/34
= 6 9/17
How many more drapery pieces than upholstery pieces does Brandon have = 708 / 85 - 222/34
= (24072-18204) / 2890
= 5,868 / 2890
= 2.03 pieces
Therefore, the number of more drapery pieces than upholstery pieces does Brandon have is 2.03 pieces
Learn more about fraction:
https://brainly.com/question/2929160
#SPJ1
Find a third degree polynomial equation with coefficients that has roots -4 and 6 + i.
Answers
The third-degree polynomial equation with roots -4 and 6 + i is P(x) = (x + 4)(x - 6 - i)(x - 6 + i) or expanded form \(P(x) = x^3 - 8x^2 + 13x + 148\).
Let's denote the polynomial equation as \(P(x) = (x - r_1)(x - r_2)(x - r_3)\), where \(r_1 = -4, r_2 = 6 + i,\ and\ r_3 = 6 - i\).
Expanding the equation, we have:
\(P(x) = (x - (-4))(x - (6 + i))(x - (6 - i))\\P(x) = (x + 4)(x - 6 - i)(x - 6 + i)\\P(x) = (x + 4)((x - 6) - i)((x - 6) + i)\\P(x) = (x + 4)((x - 6)^2 - i^2)\\P(x) = (x + 4)((x - 6)^2 + 1)\\P(x) = (x + 4)(x^2 - 12x + 36 + 1)\\P(x) = (x + 4)(x^2 - 12x + 37)\\P(x) = x^3 - 8x^2 + 13x + 148\)
Therefore, the third-degree polynomial equation with the given roots is:
\(P(x) = x^3 - 8x^2 + 13x + 148\)
To know more about polynomial, refer here:
https://brainly.com/question/32536755
#SPJ4
The north pole is in the middle of the ocean. A
person at
sea level at the north pole would be 3,949 miles from
the center of the earth. The sea floor below the north
pole is at an elevation of approximately -2.7 miles. The
elevation of the south pole is about 1.7 miles. How far is
a person standing on the south pole from a submarine
at the sea floor below the north pole?
Answers
Answer:
7,897 miles
Step-by-step explanation:
3949-2.7=3946.3
3949+1.7=3950.7
3946.3+3950.7=7897
What is the equation of a line that passes through the point (2, −10) and is parallel to 14x+2y=6?
Answers
The the equation of a line that passes through the point (2, −10) and is parallel to 14x+2y=6 is 7x + y + 8 = 0.
A straight line is just a line with no curves. So, a line that extends to both sides till infinity and has no curves is called a straight line.
The equation of a line parallel to a given line will have the same slope as the given.
The equation of a line having a slope m and passing through the point (x', y') is written as
y - y' = m (x - x').
This is called point - slope equation of a straight line.
In the given equation,
14x+2y=6
⇒ 2y = -14x + 6
⇒ y = -7x + 3
Comparing it with standard equation of a straight line; y = m x + c, the slope m of the given line = -7
Therefore equation of the line parallel to the given line and passing through point (x', y') = (2, -10) would be:
y - (-10) = -7x + 2
⇒ y + 10 = -7x + 2
⇒ 7x + y + 8 = 0
Hence the required equation of line 7x + y + 8 = 0
To learn more about straight line visit:
brainly.com/question/27560536
#SPJ1