angles M and N are supplementary find angle M if angle N=27
Answers
Answer:
153°
Step-by-step explanation:
Supplementary = 180 degrees
180 - 27 = 153 degrees
Answer:
153 degrees
Step-by-step explanation:
When two angles are supplementary, their angle measures must add up to 180 degrees. Therefore:
M+N=180
M+27=180
M=180-27=153
Hope this helps!
Related Questions
An amusement part sells children
tickets, c, for $15 and adult tickets,
a, for $22. On Monday they sold
438 tickets and earned a total of
$7,067. How many children and
adult tickets did they sell on
Monday?
Answers
Then,x+147 = number of children's tickets
8/1 = (x+147) / x
x + 147 = 8x
7x = 147
x = 21
They sold 21 adult tickets and 168 children's tickets.
a number is greater than 12
Answers
Answer:
anything above 12
Step-by-step explanation:
would be greater than 12. 13, 14, 16...etc
Answer:
n > 12
Step-by-step explanation:
Represent the number by n. Then "a number is greater than 12" expressed symbolically is n > 12.
answer and or help would be much appreciated work is due and needs to be submitted
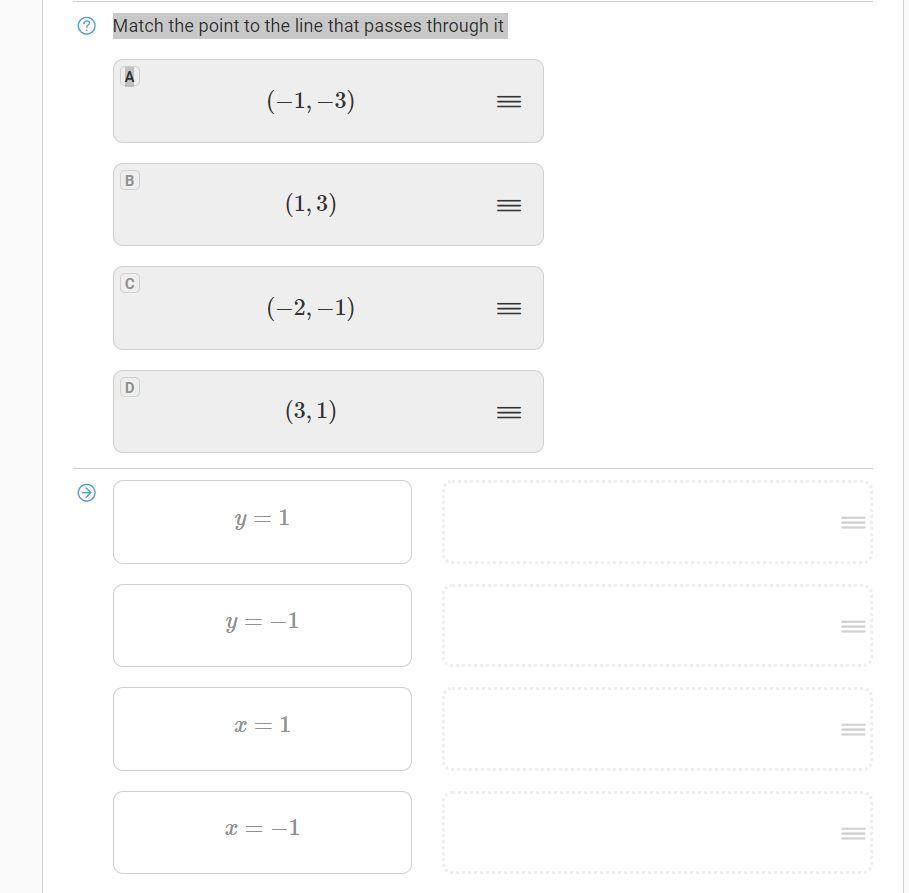
Answers
Answer:
1. D
2. C
3. B
4. A
Step-by-step explanation:
just match up the number y is on the right side and x on the left side like this (x,y)
State the degree and leading coefficient of each polynomial in one variable. If not a polynomial in one variable, explain why.
3x^4+6x^3-x^2+12
Answers
Answer:
Step-by-step explanation:
3x^4+6x^3-x^2+1...............
Is -9 terminating, repeating, or neither?
Answers
Answer:
If It -9 then it neither but if it is -1/9 it is repeating or any 9 denominator is repeating
Step-by-step explanation:
find the exact values of the sine, cosine, and tangent of the angle. 255° = 300° − 45°
Answers
The exact values of the sine, cosine, and tangent of the angle 255° are -1/√2, 1/√2, and -1, respectively.
To find the exact values of the sine, cosine, and tangent of the angle 255°, we can use the identity that relates the trigonometric functions of an angle to the trigonometric functions of its complement.
By expressing 255° as the sum of 300° and -45°, we can determine the exact values of the trigonometric functions for the given angle.
We know that the sine, cosine, and tangent of an angle are periodic functions, repeating every 360 degrees. To find the exact values of the trigonometric functions for 255°, we can express it as the sum of 300° and -45°, where 300° is a multiple of 360°.
Since the sine, cosine, and tangent functions are odd or even functions, we can use the values of the trigonometric functions for 45° to determine the values for -45°.
For 45°:
sin(45°) = cos(45°) = 1/√2
tan(45°) = 1
Since cosine is an even function, cos(-45°) = cos(45°) = 1/√2.
Since sine is an odd function, sin(-45°) = -sin(45°) = -1/√2.
Using the definition of tangent as the ratio of sine to cosine, tan(-45°) = sin(-45°) / cos(-45°) = (-1/√2) / (1/√2) = -1.
Therefore, for the angle 255°:
sin(255°) = -1/√2
cos(255°) = 1/√2
tan(255°) = -1
Learn more about trigonometric functions here:
brainly.com/question/28483432
#SPJ11
binomial a lottery will be held. from 1000 numbers, one will be chosen as the winner. a lottery ticket is a number between 1 and 1000. how many tickets do you need to buy in order for the probability of winning to be at least 50%?
Answers
we need to buy at least 694 tickets to have a probability of winning at least 50%.
We can use the binomial distribution formula to solve this problem. Let X be the number of tickets we need to buy to have a probability of winning at least 50%. Then:
P(X ≥ 1) ≥ 0.5
This means that the probability of winning with at least one ticket is at least 50%. We can find this probability using the complement rule:
P(X ≥ 1) = 1 - P(X = 0)
The probability of not winning with any ticket is:
P(X = 0) = (999/1000)^n
where n is the number of tickets we buy. Therefore:
1 - (999/1000)^n ≥ 0.5
Simplifying this inequality, we get:
(999/1000)^n ≤ 0.5
Taking the logarithm of both sides, we get:
n log(999/1000) ≤ log(0.5)
n ≥ log(0.5) / log(999/1000)
n ≥ 693.15
Therefore, we need to buy at least 694 tickets to have a probability of winning at least 50%.
Learn more about Probability
brainly.com/question/30034780
#SPJ11
plz help will mark as brainliest

Answers
Answer:
(i), (ii) and (v) are the linear pairs in the following angles.
Step-by-step explanation:
Linear pair refers to adjacent supplementary angles whose sum = 180 degrees
Hope this helps!
Please mark as brainliest
Step-by-step explanation:
d is the answer hope it will help u
1. Which inequality matches the graph ?*

Answers
Answer: x < -1.
Step-by-step explanation: That is the answer. Everything less than -1.
Answer:
x < -1
Step-by-step explanation:
Your answer is correct: it has an empty circle (which means it is either < or > not including). The arrow also points to the left, meaning less than or <
Find x to the nearest tenth.

Answers
B. 14.4
Step-by-step explanation:Hi there !
Angle Bisector Theorem =>
=> 8.3/6.7 = x/11.6
x = 8.3×11.6/6.7
= 96.28/6.7
= 14.37
≈ 14.4
Good luck !
can someone help me please im desperate

Answers
Explanation: A linear function would be a diagonal line from left to right either moving up or down in direction. An exponential function would be a straight line on the x axis from left or right until it reaches y axis, then a sharp curve up or down. A quadratic function would be a U shape either facing up or down.
Linear equation: y = mx + b
Exponential equation: y = abˣ
Quadratic function: y = axˣ + bx + c
The graph listed in the picture would be a quadratic function according to the explanation.
find the volume of the solid enclosed by the paraboloid z = 3 + x^2 + (y − 2)^2 and the planes z = 1, x = −2, x = 2, y = 0, and y = 2.
Answers
The volume is (8π/3) cubic units.
How to find volume?To find the volume of the solid enclosed by the paraboloid z = 3 + x² + (y − 2)²and the planes z = 1, x = −2, x = 2, y = 0, and y = 2, we need to use a triple integral.
The limits of integration for x, y, and z are as follows:
-2 ≤ x ≤ 2
0 ≤ y ≤ 2
1 ≤ z ≤ 3 + x² + (y − 2)²
Therefore, the triple integral for the volume is:
V = ∫∫∫ (3 + x² + (y − 2)²- 1) dx dy dz, where the limits of integration are as given above.
Simplifying this integral, we get:
V = ∫∫∫ (x² + (y − 2)²) dx dy dz
Using cylindrical coordinates, we can express x and y in terms of r and theta:
x = r cos(theta)
y = r sin(theta)
The limits of integration for r and theta are:
0 ≤ r ≤ 2
0 ≤ theta ≤ 2π
Substituting these values into the triple integral, we get:
V = ∫∫∫ r² dr dtheta dz
Integrating with respect to r and theta first, we get:
V = ∫0² ∫0^2π (r²) dtheta dr ∫1^(3 + r²- 4r sin(theta)) dz
Simplifying the innermost integral, we get:
V = ∫0²∫0^2π (r²) dtheta dr (2 + r² - 4r)
Evaluating the integrals, we get:
V = ∫0^2 (2πr² - 4π\(r^3\) + (4/3)\(r^4\)) dr
V = (8π/3)
Therefore, the volume of the solid enclosed by the paraboloid z = 3 + x² + (y − 2)² and the planes z = 1, x = −2, x = 2, y = 0, and y = 2 is (8π/3) cubic units.
Learn more about volume
brainly.com/question/1578538
#SPJ11
the number y of bacteria in a colony grows according to the differential equation dy/dt=0.06y. Which of the following is a possible formula for y? (A) y(t) = 0.06 (B) y(t) = 20.06 (C) y(t) = 0.06 (D) y(t) = 5e0.06 (E) None of these
Answers
the formula for y is y(t) = Ce^(0.06t), where C is a positive constant.
What is Equation?
In mathematics, an equation is a statement that asserts the equality of two expressions that are joined by the equal sign "=".
The differential equation dy/dt = 0.06y represents the growth of a bacterial colony, where y is the number of bacteria and t is the time. To find the formula for y, we need to solve this differential equation.
The given equation is separable, meaning we can separate the variables y and t on opposite sides of the equation:
dy/y = 0.06 dt
Integrating both sides, we have:
∫(1/y) dy = ∫0.06 dt
ln|y| = 0.06t + C
Here, C is the constant of integration. We can write it as ln|C|, where C > 0.
Now, exponentiating both sides, we get:
|y| = e^(0.06t + ln|C|)
Since y represents the number of bacteria, it cannot be negative. Therefore, we can drop the absolute value signs:
y = Ce^(0.06t)
So, the formula for y is y(t) = Ce^(0.06t), where C is a positive constant.
None of the given options (A) through (E) match this form exactly. However, option (D) y(t) = 5e^(0.06) is very close. It should be y(t) = Ce^(0.06t), so option (D) is the closest representation among the given options.
To learn more about Equation from the given link
https://brainly.in/question/56082459
#SPJ4
For a particular sequence a₁ = 3, a₂ = 5 and aₙ = aₙ ₋ ₁ – aₙ ₋ ₂, for n ≥ 3. What is
the 2015th term in this sequence?
Answers
Answer:
a=3.5,d=0 and n=101
a
n
=a+(n−1)×d
a
n
=3.5+100×0
a
n
=3.5Step-by-step explanation:
A bag contains four red marbles, nine green marbles, four blue marbles, and three yellow marbles. If Lisa draws a random marble
from the bag, what is the probability that it will be a red, green, or blue marble?
Answers
Answer:
The answer is 17/20
Step-by-step explanation:
idk
Answer (*shrugs*):
Red = 1/5
Green = 9/20
Blue = 1/5
BALLOON The angle of depression from a hot air balloon to a person on the ground is 36°. When the person steps back 10 feet, the new angle of depression is 25°. If the person is 6 feet tall, how far above the ground is the hot air balloon to the nearest foot?
Answers
The distance of the jot air balloon to ground is 21.62 ft.
Here, we have,
In triangle ACB:
tan36° = x/y
x = y tan36°
In triangle ADB:
tan25° = x/y + 12
x = y+12 * tan25°
Therefore equating both equations gives:
y tan36° = y+12 * tan25°
y tan36° = y tan25° + 12tan25°
so, we get,
y = 21.50 ft
Therefore x = 21.50*tan(36) = 15.62 ft
The distance of the jot air balloon to ground = 15.62 + 6 = 21.62 ft
Hence, The distance of the jot air balloon to ground is 21.62 ft.
To learn more trigonometry click:
brainly.com/question/26719838
#SPJ1
the following are ages of 17 of the signers of the declaration of independence. 34, 32, 50, 53, 42, 52, 34, 27, 39, 50, 35, 38, 33, 55, 44, 35, 49 send data to calculator find 10th and 75th percentiles for these ages. (a) the 10th percentile: (b) the 75th percentile:
Answers
10th percentile is 0 and 75th percentile is 100 for the given 17 ages of signers.
Given the ages of 17 of the signers of the declarations of independence.
34, 32, 50, 53, 42, 52, 34, 27, 39, 50, 35, 38, 33, 55, 44, 35, 49
What is percentile?
The value that a specific percentage falls under is known as the percentile. Ben, for instance, is the fourth tallest child in a group of 20, and eighty percent of the kids are shorter than you. As a result, Ben is in the 80th percentile.
When comparing exact values or numbers to other numbers from the given data, or when determining how accurate a number is, we use the percentile calculation. Although percentile and percentage are often confused, they are two distinct concepts.
A percentile is a figure below the % discovered from the provided data, but a percentage is when the fraction is treated as one phrase. Percentile formulas are typically useful in finding test scores or biometric measurements in daily life. The percentile formula is as follows:
Percentile equals (n/N)*100.
Percentile(x) = (Number of Values Below “x” / Total Number of Values) × 100
Percentile(10) = (Number of Values Below “10” / Total Number of Values) × 100
Number of values below 10 = 0
Percentile(10) = 0
Percentile(75) = (Number of Values Below “75” / Total Number of Values) × 100
Number of values below 75 = 17
Percentile(75) = 100.
To know more about percentile here:
https://brainly.com/question/1561673
#SPJ4
Water flows onto a flat surface at a rate of 15 cm3 is forming a circular puddle 10 mm deep. How fast is the radius growing when the radius is: 1 cm ? Answer= ____ 10 cm ? Answer= ____ 100 cm ? Answer= ____
Answers
When the radius is 1 cm, the rate of growth is approximately 0.15 cm/s. When the radius is 10 cm, the rate of growth is approximately 0.015 cm/s. Finally, when the radius is 100 cm, the rate of growth is approximately 0.0015 cm/s.
The rate at which the radius of the circular puddle is growing can be determined using the relationship between the volume of water and the radius.
To find the rate at which the radius is growing, we can use the relationship between the volume of water and the radius of the circular puddle. The volume of a cylinder (which approximates the shape of the puddle) is given by the formula V = πr^2h, where r is the radius and h is the height (or depth) of the cylinder.
In this case, the height of the cylinder is 10 mm, which is equivalent to 1 cm. Therefore, the volume of water flowing onto the flat surface is 15 cm^3. We can now differentiate the volume equation with respect to time (t) to find the rate of change of the volume, which will be equal to the rate of change of the radius (dr/dt) multiplied by the cross-sectional area (πr^2).
dV/dt = πr^2 (dr/dt)
Substituting the given values, we have:
15 = πr^2 (dr/dt)
Now, we can solve for dr/dt at different values of r:
When r = 1 cm:
15 = π(1)^2 (dr/dt)
dr/dt = 15/π ≈ 4.774 cm/s ≈ 0.15 cm/s (rounded to two decimal places)
When r = 10 cm:
15 = π(10)^2 (dr/dt)
dr/dt = 15/(100π) ≈ 0.0477 cm/s ≈ 0.015 cm/s (rounded to two decimal places)
When r = 100 cm:
15 = π(100)^2 (dr/dt)
dr/dt = 15/(10000π) ≈ 0.00477 cm/s ≈ 0.0015 cm/s (rounded to four decimal places)
Therefore, the rate at which the radius is growing when the radius is 1 cm is approximately 0.15 cm/s, when the radius is 10 cm is approximately 0.015 cm/s, and when the radius is 100 cm is approximately 0.0015 cm/s.
Learn more about Circular surfaces here:
brainly.com/question/29885830
#SPJ11
At a constant of 80 kilometres per hour, it would take 35 years to travel over the entire road network of the world. Taking a year as 365 days, calculate the length of the road network of the world, giving your answer in standard form.
Answers
Answer:
115
Step-by-step explanation:
1.1. In a famous joke, a rather lazy student tosses a coinand decides what to do next. If it turns up heads, play a computergame. If tails, watch a video. If it stands on its edge, do thehomework. If it hangs in the air, prepare for an exam.(a) Which events should be assigned probability 0, probability1, and some probability strictly between 0 and 1?(b) What probability between 0 and 1 would you assign to theevent "watch a video," and how does it help you to define "a faircoin"?1.2. A new software package is being tested by specialists.Every day, a number of defects is found and corrected. It isplanned to release this software in 30 days. Is it possible topredict how many defects per day specialists will be finding at thetime of the release? What data should be collected for thispurpose, what is the predictor, and what is the response?
Answers
The event "If it hangs in the air, prepare for an exam." will be assigned probability 0. No event should be assigned probability 1. The events "If it turns up heads, play a computer game" and "If tails, watch a video." can be assigned some probability strictly between 0 and 1.
The probability of watching a video would be 0.5.
Also, the answer to the second question is that the data to be collected should include the number of defects found and corrected each day during the testing process.
1.1(a) In the given joke, the events and their probabilities can be assigned as follows:
- Probability 0: "If it hangs in the air, prepare for an exam." This is an impossible event, as a coin cannot hang in the air.
- Probability 1: There's no event with a certainty of happening in this scenario, so none should be assigned probability 1.
- Probability strictly between 0 and 1: "If it turns up heads, play a computer game" and "If tails, watch a video." These events have a non-zero probability of happening, but they are not certain.
1.1(b) To assign a probability between 0 and 1 to the event "watch a video," we need to consider the concept of a fair coin.
A fair coin has an equal chance of landing on heads or tails. So, the probability of watching a video (tails) would be 0.5.
This helps define a fair coin as one that has a 50% chance of landing on either side.
1.2 Predicting the number of defects per day at the time of release may be possible, but it depends on the data collected and the methodology used. The data to be collected should include the number of defects found and corrected each day during the testing process.
The predictor in this case is the number of days that elapsed since testing began, while the response is the number of defects found and corrected daily. A statistical model, such as regression analysis, can be used to predict the number of defects per day at the time of the release based on the collected data.
Learn more about probability:
https://brainly.com/question/25870256
#SPJ11
Use the shell method to find the volume of the solid generated by revolving the region bounded by y=6x−5,y=√x, and x=0 about the y-axis
The volume is _____cubic units. (Type an exact answer, using π as needed)
Answers
To find the volume of the solid generated by revolving the region bounded by y=6x−5, y=√x, and x=0 about the y-axis using the shell method, we integrate the circumference of cylindrical shells.
The integral for the volume using the shell method is given by:
V = 2π ∫[a,b] x(f(x) - g(x)) dx
where a and b are the x-values of the intersection points between the curves y=6x−5 and y=√x, and f(x) and g(x) represent the upper and lower functions respectively.
To find the intersection points, we set the two functions equal to each other:
6x - 5 = √x
Solving this equation, we find that x = 1/4 and x = 25/36.
Substituting the values of a and b into the integral, we have:
V = 2π ∫[1/4,25/36] x((6x-5) - √x) dx
Evaluating this integral will give us the volume of the solid.
To know more about the shell method click here: brainly.com/question/30401636
#SPJ11
Re-write the quadratic function below in Standard Form
y= 4(x + 8)(x - 2)
Answers
Answer:
4x^2+24x-64
Step-by-step explanation:
First you multiply (x+8) by (x-2). You can use this using the FOIL method which stands for first, outer, inner, last. Through this method you would multiply x by x first and get x^2, then x by -2 and get -2x, then 8 by x and get 8x, and finally 8 by -2 and get -16. You then add this all together and get x^2-2x+8x-16 or x^2+6x-16.
Now all you have to do is multiply each term by 4 and get 4x^2+24x-64 using the distributive property.
we have 9 balls of colours red, green and blue, 3 balls of each color (balls of the same color are identical). we want to place them in the sequence in such a way that no two blue balls are next to each other. how many ways do we have to do it?
Answers
There are 347,760 ways to arrange the 9 balls of colors red, green, and blue such that no two blue balls are next to each other. The principle of inclusion-exclusion is used to solve this problem.
First, we calculate the total number of ways to arrange the 9 balls without any restrictions. This can be done using the formula for permutations of n objects, which is n! (n factorial) in this case. So we have:
9! = 362,880
Next, we calculate the number of ways to arrange the balls with two blue balls next to each other. We can treat the two blue balls as a single object and arrange the remaining 7 objects in 7! ways. However, we also need to consider the 3 different ways to choose which two blue balls are next to each other. So we have:
3 x 7! = 15,120
Finally, we need to subtract the number of arrangements with two blue balls next to each other from the total number of arrangements to get the number of arrangements without any two blue balls next to each other:
9! - 3 x 7! = 347,760
Therefore, there are 347,760 ways to arrange the 9 balls of colors red, green, and blue such that no two blue balls are next to each other.
Learn more about inclusion-exclusion at
brainly.com/question/10927267
#SPJ4
I need help with these problems please.

Answers
Answer:
10 scare crows 3 witches and 4 ghosts
Urn A contains seven white balls and five black balls. Urn B contains four white balls and six black balls. A ball is drawn from Urn A and then transferred to Urn B. A ball is then drawn from Urn B. What is the probability that the transferred ball was black given that the second ball drawn was black
Answers
Answer:
P(X/Y) = 0.4545
Step-by-step explanation:
Let's call X that the transferred ball is black, X' that the transferend ball is white and Y the event that the second ball drawn is black.
The probability that the transferred ball was black given that the second ball drawn was black is equal to:
P(X/Y) = P(X∩Y)/P(Y)
Where P(Y) = P(X∩Y) + P(X'∩Y)
Then, the probability P(X∩Y) that the transferred ball is black and the second ball drawn is black is equal to:
P(X∩Y) = (5/12)*(7/11) = 0.2651
Because the urn A has 12 balls and 5 of them are black, then if the transferred ball is black, the urn B will contain 11 balls and 7 of them will be black balls.
At the same way, the probability P(X'∩Y) that the transferred ball is white and the second ball drawn is black is equal to:
P(X'∩Y) = (7/12)*(6/11) = 0.3181
Because the urn A has 12 balls and 7 of them are white, then if the transferred ball is white, the urn B will contain 11 balls and 6 of them will be black balls.
So, P(Y) and P(X/Y) are equal to:
P(Y) = 0.2651 + 0.3181
P(Y) = 0.5832
P(X/Y) = 0.2651/0.5832
P(X/Y) = 0.4545
Solve the system.
x - 5y + 4z=27
4x-3y-z-23
3x + 3y - 6z=-9
Answers
Answer:
Step-by-step explanation:
Step by step solution of a set of 2, 3 or 4 Linear Equations using the Substitution Method x-5y+4z=27,4x-3y-z=23,3x+3y-6z=-9 Tiger Algebra Solver.
Naomi reads 9 pages in 27 minutes, 12 pages in 36 minutes, 15 pages in 45 minutes, and 50 pages in 150 minutes
Answers
Answer:
It is proportional. They are all multiplied by three. (9*3=27)
Step-by-step explanation:
pleaseeee explain !!!

Answers
A is the answer because if we want the unit rate we do
2/3÷2/3 and 15 1/5, we can turn 15 1/5 into a improper fraction first so 76/5 and we do 76/5 ÷2/3 which is equal to
76/5×3/2=114/5
114/5 simplifies into 24 4/5.
so Naomi can travel 24 4/5 gal per mile.
Hope this helps!
what is the diameter of 100km
Answers
Answer: The diameter of a circle is the distance across the circle passing through the center.
To find the diameter of a circle with a radius of 100 km, we can simply double the radius, since the diameter is twice the length of the radius.
Therefore, the diameter of a circle with a radius of 100 km is:
2 x 100 km = 200 km
So the diameter is 200 km.
Step-by-step explanation:
Help please!! I’m timed on this. No it’s not for a grade.

Answers
Answer:
D
Step-by-step explanation: