An urn contains 15 white balls and 3 green balls. A sample of seven is selected at random. What is the probability that the sample contains at least one green ball?
a) 0.471814
b) 0.797794
c) 0.528186
d) 0.000094
e) 0.999906
Answers
The probability that the sample contains at least one green ball when a sample of seven balls is selected at random from an urn that contains 15 white balls and 3 green balls is an option (c) 0.528186.
The formula to find the probability that the sample contains at least one green ball when a sample of seven balls is selected at random from an urn is given by P(at least one green ball) = 1 - P(no green ball)P(no green ball) = (15C7)/(18C7) = 0.471814
Therefore, P(at least one green ball) = 1 - 0.471814= 0.528186
Hence, the probability that the sample contains at least one green ball when a sample of seven balls is selected at random from an urn that contains 15 white balls and 3 green balls is an option (c) 0.528186.
You can learn more about probability at: brainly.com/question/11034287
#SPJ11
Related Questions
look at the shaded triangle in picture it. why can you use the expression 32 - x to represent the base of the triangle in yards
Answers
The expression 32 - x can be used to represent the base of the triangle in yards, where x is the length of the side opposite to the base.
The shaded triangle in the picture can be represented using the expression 32 - x to represent the base of the triangle in yards. This expression can be represented using a formula, which is B = 32 - x, where B is the base of the triangle in yards and x is the length of the side opposite to the base. For example, if the length of the side opposite to the base is 5 yards, then the base of the triangle would be 32 - 5 = 27 yards. Therefore, the expression 32 - x represents the base of the triangle in yards, where x is the length of the side opposite to the base.
Learn more about triangle here:
https://brainly.com/question/2773823
#SPJ1
Complete quetion:
How can you use the expression 32 - x to represent the base of the triangle in the picture in yards?
Please see the image below(math)
Answers
Answer:
21
Step-by-step explanation:
If a line parallel to one side of a triangle intersects the other two sides of the triangle, then the line divides these two sides proportionally.
AD AH
----- = ---------
AB AH +y
3 9
---- = ------
10 9+y
Using cross products:
3(9+y) = 9*10
27+3y = 90
3y = 90-27
3y =63
y = 63/3
y = 21
Answer:
y = 21
Step-by-step explanation:
According to the Side Splitter Theorem, if a line parallel to one side of a triangle intersects the other two sides, then this line divides those two sides proportionally.
Therefore, according to the Side Splitter Theorem:
\(\boxed{\sf AD : DB = AH : HC}\)
From inspection of the given triangle, the lengths of the line segments are:
AD = 3DB = 7AH = 9HC = yTo find the value of y, substitute the given line segment lengths into the proportion and solve for y:
\(\begin{aligned}\sf AD : DB &=\sf AH : HC\\\\3:7&=9:y\\\\\dfrac{3}{7}&=\dfrac{9}{y}\\\\3 \cdot y&=9 \cdot 7\\\\3y&=63\\\\\dfrac{3y}{3}&=\dfrac{63}{3}\\\\y&=21\end{aligned}\)
Therefore, the value of y is 21.
Use the point-slope formula to write an equation of the line that passes through (-4, 4) and has a slope of m=0. Write the answer in slope-intercept form (if
possible)
Answers
Answer:
y = 4
Step-by-step explanation:
When given a point and a slope, we use slope-intercept formula:
y - y1 = m (x - x1)
m = slope point: (-4,4)
y - y1 = m (x - x1)
y - 4 = 0 (x - 1)
y - 4 = 0x + 0
+ 4 + 4
y = 4
The answer can't be written in slope-intercept form, as the 0"s cancel out.
Hope this helps!
"Ready
Vicki sketches a right triangle with legs of lengths x and y and a hypotenuse of length z. She writes an equation that
relates x, y, and z. Then, she writes an expression for the length of the hypotenuse. Which expression does she write?
x² + y²
C
x? + 22
/xty
Answers
Answer:
sqrt(x^2+y^2)
Step-by-step explanation:
x^2+y^2=z^2 (Pythagorean theorem)
sqrt(x^2+y^2)=sqrt(z^2)
sqrt(x^2+y^2)=z
Helpppppppppppppppppp is this right
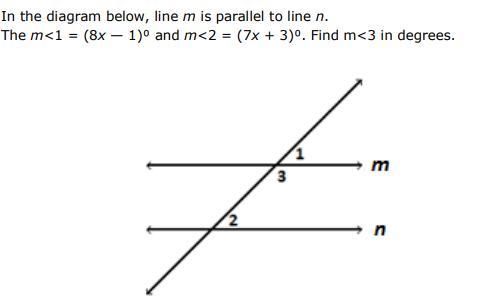
Answers
Answer:
The first one is B and the second one is correct
Step-by-step explanation:
Answer:
I think 1 is actually B and 2 is right -Your friend, Bill Cipher
Step-by-step explanation:
In a randomly generated list of numbers from 0 to 6 what is the chance that each number will occur
Answers
Answer:
In fractions, each number has a 1/6 chance of occuring. In decimals, that is around 16.6 repeating percent.
Answer:
1/7
The correct answer is 1/7
The sum of 14 and a number x is equal to 16.
Answers
Answer:
Equation: 14 + x = 16
The unknown variable: x = 2
Step-by-step explanation:
The sum of 14 and a number x:
14 + x
is equal to 16
14 + x = 16
14 + x = 16
x = 16 - 14
x = 2
A 6 foot ladder is placed against a wall with its base 2 feet from the wall. How high up the wall is the top of the ladder?
Answers
Answer:
5.66 feet
Step-by-step explanation:
a^2 + b^2 = c^2
2^2 +b^2 = 6^2
square root of (36-4) = b
b= 5.66 feet
You want to prove a theroum in a two coulum proof. You start with your given statement and list deductions in the left hand column. What are the tree main types of reasoning you will use for reasons in the right hand column?
Answers
Answer:
Definitions, postulates, and theorems.
Step-by-step explanation:
- Definition: This is a statement that describe the meanings of the terms being used.
- Postulate: This is a statement that is assumed true without proof. It is a statement that is taken to be "clearly true".
- Theorem: This is a statement that is never assumed to be true until it is proven so. It depends strongly on proofs.
Jax came to your bank to borrow 8,500 to start a new business. Your bank offers him a 30-month loan with an annual simple interest rate of 4.35%
Answers
a) The simple interest for the loan is $927.19.
b) The total amount that Jax will have to pay at the end of 30 months is $9,427.19.
a) To calculate the simple interest for the loan, we can use the formula:
Simple Interest = Principal x Rate x Time
where Principal is the amount borrowed, Rate is the annual interest rate, and Time is the duration of the loan in years.
Since the loan is for 30 months, which is equivalent to 2.5 years, we can substitute the given values:
Simple Interest = 8,500 x 0.0435 x 2.5 = $927.19
b) To determine the total amount that Jax will have to pay at the end of 30 months, we need to add the simple interest to the original amount borrowed. The total amount can be calculated using the formula:
Total Amount = Principal + Simple Interest
Substituting the given values:
Total Amount = 8,500 + 927.19 = $9,427.19
In summary, Jax will have to pay $927.19 in simple interest and a total of $9,427.19 at the end of 30 months to repay the 8,500 loan with an annual simple interest rate of 4.35%.
To learn more about interest click on,
https://brainly.com/question/31709159
#SPJ1
If <1=(7−19)°and <2=(+5)°, find the <2
If m<5 = 42° and m<1 = 117°, find m
If M is the midpoint of XY, find the coordinates of X if M(-3,-1) and Y(-8, 6).
Find the distance between the two points. Round to the nearest thousandth.(-8, -2) and (6, -1)
If DE = 4x –1, EF = 9, and DF = 9x –22, find the value of x.
Answers
Answer:
We know that the section formula states that if a point P(x,y) lies on line segment AB joining the points A(x
1
,y
1
) and B(x
2
,y
2
) and satisfies AP:PB=m:n, then we say that P divides internally AB in the ratio m:n. The coordinates of the point of division has the coordinates
P=(
m+n
mx
2
+nx
1
,
m+n
my
2
+ny
1
)
Let C(1,1) divides the line segment AB joining the points A(−2,7) and B(x
2
,y
2
) in the ratio 3:2, then using section formula we get,
C=(
m+n
mx
2
+nx
1
,
m+n
my
2
+ny
1
)
⇒(1,1)=(
3+2
3x
2
+(2×−2)
,
3+2
3y
2
+(2×7)
)
⇒(1,1)=(
5
3x
2
−4
,
5
3y
2
+14
)
⇒1=
5
3x
2
−4
,1=
5
3y
2
+14
⇒5=3x
2
−4,5=3y
2
+14
⇒3x
2
=5+4,3y
2
=5−14
⇒3x
2
=9,3y
2
=−9
⇒x
2
=
3
9
,y
2
=−
3
9
⇒x
2
=3,y
2
=−3
Hence, the point B(x
2
,y
2
) is B(3,−3).
The phone company Blurizon has a monthly cellular plan where a customer pays a flat fee for unlimited voice calls and then a certain amount per GB of data used. If a customer uses 12 GB, the monthly cost will be $72. If the customer uses 38 GB, the monthly cost will be $150. A) Find an equation in the form y
Answers
The equation in the form y is mx + b is: z = xy + x = 3x + 36
Given:The phone company Blurizon has a monthly cellular plan where a customer pays a flat fee for unlimited voice calls and then a certain amount per GB of data used.Cost of 12 GB is $72.Cost of 38 GB is $150.Let,The flat fee for unlimited voice calls = $ xThe cost per GB of data used = $ yMonthly Cost = $ z (dependent variable)
Hence, the equation in the form y = mx + b is z = xy + x which is the equation of a line in slope-intercept form, where m is the slope and b is the y-intercept. Here, the slope is the cost per GB of data used (y) and the y-intercept is the flat fee for unlimited voice calls (x).
So, using the given data:When the customer uses 12 GB, the monthly cost will be $72, hence72 = 12y + x 1.....(i)When the customer uses 38 GB, the monthly cost will be $150, hence150 = 38y + x 2....(ii)To get the value of y, we can eliminate the variable x using either of the above two equations:
Subtract equation (i) from equation (ii), we get,78 = 26y => y = 3So, x can be found by substituting the value of y in equation (i):72 = 12(3) + x=> x = 36Thus, the equation in the form y = mx + b is:z = xy + x = 3x + 36
To know more about form refer here:
https://brainly.com/question/29474217#
#SPJ11
There are four students named A,B,C, and D. All four of them are loss averse over money, with the same value function for money: v(x dollars )={√x x ≥ 0
{-2√-x x < 0
All three of them are also loss averse over mugs, with the same value function for mugs:
v(y mugs)={3y y ≥ 0
{4y y < 0
Total utility is the sum of the gain/loss utility for mugs and the gain/loss utility for money. The reference point is the status quo, that is, a person's initial endowment. Student A owns a mug and is willing to sell it for a price of a dollars or more. Student B does not own a mug and is willing to pay up to b dollars for buying it. Student C does not own a mug and is indifferent between getting a mug and getting c dollars. Student D is indifferent between losing a mug and losing d dollars.
1. Solve for a,b,c, and d.
2. Instead, suppose A, B, C, and D are only loss averse over mugs, but not over money. That is, their value function for money is instead:
v(x dollars)={√x x ≥ 0
{-√-x x < 0
and their value function for mugs remains:
v(y mugs)={3y y ≥ 0
{4y y < 0
Solve for a,b,c, and d.
3. Instead, suppose A,B,C, and D are not loss averse:
v(x dollars)={√x x ≥ 0
{-√-x x < 0
and v(y mugs)=3y
Solve for a,b,c, and d.
4. Suppose A, B, C, and D are not loss averse (as in the previous question), but their value for a mug varies with ownership. Specifically, the value of the mug is 3 for someone who does not currently own the mug, and 4 for someone who currently owns a mug. Solve for a,b,c, and d.
Answers
As per the question, All four students A, B, C, and D are loss-averse over money and have the same value function as below:v(x dollars)={√x x ≥ 0 {-2√-x x < 0They are also loss averse over mugs and have the same value function.
v(y mugs)={3y y ≥ 0
{4y y < 0
Now, we have to find the values of a, b, c and d as below:
- Student A owns a mug and is willing to sell it for a price of a dollars or more. i.e v(a) = v(0) + v(a-A), where A is the initial endowment of A. According to the given function, v(0) = 0, v(a-A) = 3, and v(A) = 4.
So, a ≥ A+3/2
- Student B does not own a mug and is willing to pay up to b dollars for buying it. i.e v(B-b) = v(B) - v(0), where B is the initial endowment of B. According to the given function, v(0) = 0, v(B-b) = -4, and v(B) = -3.
So, b ≤ B+1/2
- Student C does not own a mug and is indifferent between getting a mug and getting c dollars. i.e v(c) = v(0) + v(c), where C is the initial endowment of C. According to the given function, v(0) = 0, v(c) = 3.
So, c = C/2
- Student D is indifferent between losing a mug and losing d dollars. i.e v(D-d) = v(D) - v(0), where D is the initial endowment of D. According to the given function, v(0) = 0, v(D-d) = -3.
So, d = D/2
2) In this case, value function for money changes to:v(x dollars)={√x x ≥ 0
{-√-x x < 0
However, the value function for mugs remains the same:v(y mugs)={3y y ≥ 0
{4y y < 0
Therefore, values for a, b, c, and d will remain the same as calculated in part (1).
3) In this case, students are not loss-averse. Value function for money:v(x dollars)={√x x ≥ 0
{-√-x x < 0
Value function for mugs:v(y mugs)={3y y ≥ 0
The reference point is the status quo, i.e initial endowment. So,
- Student A owns a mug and is willing to sell it for a price of a dollars or more. The value of mug for A is 3 initially and he would sell it for 3 or more.
So, a ≥ A+3/2
- Student B does not own a mug and is willing to pay up to b dollars for buying it. The value of mug for B is 3 initially and he would buy it for 3 or less.
So, b ≤ B+3/2
- Student C does not own a mug and is indifferent between getting a mug and getting c dollars. The value of the mug for C is 3 initially.
So, c = 3
- Student D is indifferent between losing a mug and losing d dollars. The value of the mug for D is 3 initially.
So, d = 3
4) In this case, value function for money:v(x dollars)={√x x ≥ 0
{-√-x x < 0
Value function for mugs: Mug will have a value of 4 for someone who owns it and 3 for someone who does not own it.
The reference point is the status quo, i.e initial endowment. So,
- Student A owns a mug and is willing to sell it for a price of a dollars or more. The value of mug for A is 4 initially and he would sell it for 4 or more.
So, a ≥ A+2
- Student B does not own a mug and is willing to pay up to b dollars for buying it. The value of mug for B is 3 initially and he would buy it for 3 or less.
So, b ≤ B+3/2
- Student C does not own a mug and is indifferent between getting a mug and getting c dollars. The value of the mug for C is 3 initially and he would like to buy it for 3.
So, c = 3
- Student D is indifferent between losing a mug and losing d dollars. The value of the mug for D is 3 initially.
So, d = 3.
To know more about students visit:
https://brainly.com/question/29101948
#SPJ11
Give the slope of each line. Also, state if the lines are parallel (yes or no).
AB: y = x+ 4 CD: y = - 2
Slope of AB:
Slope of CD:
Answers
Answer:
AB slope is 1/2
CD slope is 1/3
Since the slopes of the lines aren't the same, the lines aren't parallel.
Step-by-step explanation:
i have no idea about how to do it.
Answers
The blanks are filled as follows
Step one
Equation 2x + y = 18 Isolate y,
y = 18 - 2x
How to complete the stepsStep Two:
Equation 8x - y = 22, Plug in for y
8x - (18 - 2x) = 22
Step Three: Solve for x by isolating it
8x - (18 - 2x) = 22
8x - 18 + 2x = 22
8x + 2x = 22 + 18
10x = 40
x = 4
Step Four: Plug what x equals into your answer for step one and solve
y = 18 - 2x
y = 18 - 2(4)
y = 18 - 8
y = 10
So the solution to the system of equations is x = 40 and y = 10
Learn more about system of equations at
https://brainly.com/question/25976025
#SPJ1
Suzi starts her hike at 215 feet below sea level. When she reaches the end of the hike, she is still below sea
level at -175 feet. What was the change in elevation from the beginning of Suzi's hike to the end of the
hike?
Answers
25. Tickets to a movie cost $5 for adults and $3 for students. A group of friends purchased 18 tickets for $82.00. How many adults ticket did they buy?
26. A farmhouse shelters 10 animals. Some are pigs and some are ducks. Altogether there are 36 legs. How many of each animal are there?
Please help with steps
Answers
Cost of 1 dozen peaches at 65¢ each.
Answers
Answer:
780¢
Step-by-step explanation:
A dozen = 12
so 12 * 65 = 780
Answer:
The answer is 780¢
Step-by-step explanation:
Given;Cost of each Peach = 65¢To Find;Cost of 1 dozen of peachesNow, we know that 1 dozen = 12
So,
65 × 12 = 780
Thus, The cost of 1 dozen of peaches is 780¢
-TheUnknownScientist 72
Did I graph this equation right?
Equation: P=125+50w
Answers
Answer:
yes
Step-by-step explanation:
You want a graph of P = 125 +50W.
Slope-intercept formThe given equation is in slope-intercept form. The independent variable is W, and the dependent variable is P.
Axes assignmentsUsually, the independent variable is graphed on the horizontal axis, which you have done.
The dependent variable is graphed on the vertical axis, which you have done.
The axes are correctly labeled and graduated.
InterceptThe "y-intercept" (P value) when the independent variable is zero is the constant in the equation, 125. You have correctly shown that on the graph.
SlopeThe slope of the line is the coefficient of the independent variable (W) in the equation. You have correctly shown that P increases by 50 when W increases by 1.
Yes, you properly graphed the equation.
<95141404393>
Find the term between 21 and 153
Answers
Answer:
22,23,24... 152
Step-by-step explanation:
term= between the given
an organization will give a prize to a local artist. the artist will be randomly chosen from among 7 painters, 4 sculptors, and photographers. what is the probability that the artist chosen will be a painter or a 5 photographer? write your answer as a fraction.
Answers
The probability that the artist chosen will be a painter or a photographer is 3/4
What is probability?Probability is the function that measures the chances that an outcome of a random event will be as expected. In this way you can measure how likely it is that an event will happen.
To solve this exercise the formula and the procedure that we have to use for probability is:
probability= (achieving success / possible outcomes)
Achieving success = 7 painters + 5 photographer = 12
Possible outcomes = 7 painters + 5 photographer + 4 sculptors = 16
Applying the formula to calculate the probability we get:
probability= (achieving success / possible outcomes)
probability= 12/16
Simplifying:
probability= 3/4
Learn more about probability at: brainly.com/question/251701
#SPJ4
Second Roll First Roll 1 2 3 4 5 6 1 1-1 1-2 1-3 1-4 1-5 1-6 2 2-1 2-2 2-3 2-4 2-5 2-6 3 3-1 3-2 3-3 3-4 3-5 3-6 4 4-1 4-2 4-3 4-4 4-5 4-6 5 5-1 5-2 5-3 5-4 5-5 5-6 6 6-1 6-2 6-3 6-4 6-5 6-6 Select the favorable outcomes for rolling double sixes. (6-1) (6-5) (6-6) (6-3)
Answers
Answer:
(6 - 6)
Step-by-step explanation:
Answer:
25
Step-by-step explanation:
Please help I don't want just the answer I want to know how to solve it.
Answers
Answer:
149 degrees
Step-by-step explanation:
Since m and n are parallel you need to remember the rules of transversals, this means that <1 and <2 are corresponding. Corresponding angles are always congruent, so we can solve for x by setting them equal to each other.
\(8x-1=7x+3\)
First, move the variables to one side, I will move them both to the right, but remember you can do it on either side. To do this subtract 7x from both sides
\(8x-1-7x=7x+3-7x\), then simplify
\(x-1=3\)
Next, add 1 to both sides to isolate the variable
\(x-1+1=3+1\), then simplify
\(x=4\)
Now that you know what x equals solve for angle 1, to do this plug 4 in for x in the original equation
\(8(4)-1=31\)
Finally, you can solve for <3 because <1 and <3 are supplementary. So to solve add both and set them equal to 180, in this equation let x stand for <3. \(180=31+x\), then subtract 31 from both sides \(180-31=31+x-31\) and simplify, \(149=x\). So angle 3 is equal to 149.
solving system by substitution Help ASAP
Answers
Answer:
c is 3
d is 10
Step-by-step explanation:
see photo :)
Answer:
Hello answer:
c = 3
d = 10
Step-by-step explanation:
2 × c = 6 6 + 4 = 10
10 × 3 = 30 c × 2 = 6 30 + 6 = 36
if the numerator of a fraction is larger than the denominator of the fraction in the fraction is greater than 1.
Answers
Answer:
improper fraction
Step-by-step explanation:
im not sure if this is what you're looking for but i hope it helps
The manager of a grocery store has selected a random sample of 100 customers. The average length of time it took these 100 customers to check out was 3.0 minutes. It is known that the standard deviation of the checkout time is 1 minute.
Flag question: Question 11
Question 1125 pts
Refer to Exhibit 8-2. The standard error of the mean equals _____.
Group of answer choices
.001
.01
.1
1
Answers
The standard error of the mean for this random sample of 100 customers is 0.1.
The correct option is C.
The standard error of the mean is a measure that indicates the precision or variability of the sample mean in relation to the population mean. It represents the average amount of sampling error we can expect when estimating the population means based on a sample.
To calculate the standard error of the mean, we divide the standard deviation of the population by the square root of the sample size. In this case, the standard deviation is 1 minute and the sample size is 100.
Dividing 1 by the square root of 100, we get 1/10 or 0.1. This means that the standard error of the mean for this sample is 0.1.
A smaller standard error of the mean indicates that the sample mean is a more accurate estimate of the population mean. In this case, a standard error of 0.1 suggests that the average length of time it took customers to check out may vary around the sample mean by approximately 0.1 minutes.
To learn more about the standard deviation;
brainly.com/question/23907081
#SPJ1
In a school 2/3 of the students study a language
Of those who study a language, 2/5 study french
Find the ratio of students who study French to students who do not study french. Give your answer in it simplest form.
Answers
Answer:
4:6
or 4/15 : 2/5
Step-by-step explanation:
Ellie has a gift card to buy a new computer. She says the card’s value is not enough to buy any of the computers shown in the table.
Computer Model Cost
Brand A $324
Brand B $377
Brand C $413
Brand D $391
Let v be the value of the gift card. Drag numbers and symbols to complete an inequality that best describes the value of the gift card.
Answers
The lowest price of a computer is Brand A $324
The gift card has to be less than that.
The inequality would be: v < 324
An orchand has 8 times more apple trees than pear trees. There are 981 trees in all. How many more apple trees are there
Answers
Answer:
763
Step-by-step explanation:
there are 763 more apple trees than pear trees
Step-by-step explanation:
so, first we write the words into equations.
8P = A because there are 8x apples per x pear, so to make it equal we must multiply pears by 8. P+A = 981. replacing "A" in the second equation with "8P" to get P+8P=981=9P divide both sides by 9 to get 109 pear trees. knowing this we can get 981-109=A=872 apple trees. the problem asks for A-P which we can replace the numbers to get (872)-(109)=763 more trees
Answer:122.625
Step-by-step explanation:981 divided by 8 equals 122.625
Suppose A and B begin transmission at t=0 bit times. They both detect collisions at t=245 bit times. Suppose KA=0 and KB=1. At what time does B schedule its retransmission? At what time does A begin transmission?
Answers
B schedules its retransmission for t=247 bit times, and A begins transmission at t=246 bit times.
Assuming that A and B are using a binary exponential backoff algorithm to schedule their retransmissions after detecting a collision, we can use the following steps to determine when B schedules its retransmission and when A begins transmission:
Determine the number of collision attempts made by B before it schedules its retransmission:
B starts with KA=0 and KB=1, so it will attempt transmission at time t=0 bit times.
B detects a collision at t=245 bit times, so it increments KB to KB=2 and schedules its retransmission for a random time between 0 and 2^KB-1 = 3 bit times later.
Since KB=2, B will choose a random backoff time between 0 and 3 bit times. Suppose it chooses a backoff time of 2 bit times.
B will therefore schedule its retransmission for t=245+2=247 bit times.
Determine when A begins transmission:
After detecting a collision at t=245 bit times, A increments KA to KA=1 and schedules its retransmission for a random time between 0 and 2^KA-1 = 1 bit time later.
Since KA=1, A will choose a random backoff time between 0 and 1 bit time. Suppose it chooses a backoff time of 1 bit time.
A will therefore begin transmission at t=246 bit times, which is one bit time after B schedules its retransmission at t=247 bit times.
Learn more about binary exponential backoff algorithm here
brainly.com/question/15689951
#SPJ4