An online retailer charges $30 for 12 cans of tennis balls. Which statement is correct ? Mark all that apply.
A.) The cost of 150 cans of tennis balls is $350.
B.) The cost of 100 cans of tennis balls is $250.
C.) The cost of 120 cans of tennis balls is $300.
D.) The cost of 180 cans of tennis balls is $500.
E.) The cost of 200 cans of tennis balls is $550.
F.) The cost of 250 cans of tennis balls is $625.
10 points !!
Answers
Answer:
The cost of 100 cans of tennis balls is $250
The cost of 120 cans of tennis balls is $300.
The cost of 250 cans of tennis balls is $625
Step-by-step explanation:
0/12 = 2.5 per can
100*2.5 = 250
120*2.5 = 300
250*2.5= 625
Related Questions
Solve the given differential equation by separation of variables. dP/dt =P-P2 P=
Answers
In accordance with the above assertion, the offered differential equation by variable separation is P = 1/ (k*e^t +1).
What does a math differential equation mean?A differential equation in mathematics is one that has one or more negatively influencing variables. Dy/dx provides the function's derivative. The phrase describes an equation with several ways to connect the dependent variable to one or more regressors.
dP/dt = P - P^2
1/(P - P^2)dP = dt
∫1/(P - P^2)dP = ∫dt
t + c = 1/(P - P2)dP, where c would be a constant
Use the partial fractions method to calculate the integrated on the left. We wish to rewrite 1/(P-P2) in the pattern A/P+B/(1-P) for those constants A and B since P-P2 factors to P(1-P). We therefore have:
1/[P(1-P)] = A/P + B/(1-P)
A(1-P) + BP = 1
When P is 1, we have A(1-1)+B(1)=1, or B=1.
When P is 0, we have A(1-0)+B(0)=1, or A=1.
So, we can rewrite 1/(P-P^2) as 1/P+1/(1-P).
Whilst doing the entire on the ODE's left side, we have:
∫1/(P - P^2)dP
∫[1/P + 1/(1-P)]dP
∫(1/P)dP + ∫1/(1-P)dP
ln(P) + ∫1/(1-P)dP
Make a u-substitution to perform the second integral:
u = 1-P, du = -dP
ln(P) - ∫(1/u)du
ln(P) - ln(u)
ln(P) - ln(1-P)
ln[P/(1-P)]
Reconnecting that to the ODE yields the following:
ln[P/(1-P)] = t + c
e^ln[P/(1-P)] = e^(t + c)
P/(1-P) = e^t * e^c
P/(1-P) = ke^t, where k is a constant equal to e^c
P = (1-P)ke^t
P = ke^t - Pke^t
P + Pke^t = ke^t
P(1 + ke^t) = ke^t
P = ke^t / (1 + ke^t)
P = e^t / (1/k + e^t)
P = e^t / (d + e^t), where d is a constant equal to 1/k
So, the general solution to the ODE is P = e^t / (d + e^t), where d is a constant.
p*(1-p) = k*e^t ( we say that e^k is a constant)
1-p/p = k*e^t
P = 1/ (k*e^t +1)
To know more about Differential equation visit:
https://brainly.com/question/23802083
#SPJ4
The complete question is-
Solve the given differential equation by separation of variables.
dP/dt = P - P²
please Evaluate 27 times ( 1/3) to the 3 power. A). 1 B). 3 C). 9 D). 27
Answers
Answer:
you want to follow PEMDAS so you would multiply 27 by 1/3 to get 81.003, which you would round to 81, then you would multiply 8 to the third power and you would get 512.
Step-by-step explanation:
27(1/3)^3
81^3
512
PLEASE HELP WITH MY HOMEWORK SCREEN SHOT ATTACTCHED

Answers
Answer:
first, second and fourth are all correct
Step-by-step explanation:
Please show the figure in a piece of paper

Answers
Step-by-step explanation:
If you have any dout you can ask me.

A colony of ants carried away 10 of your muffins. That was 5/9 of all of them! How many are left ?
Answers
Given that a colony of ants carried away 10 of your muffins which was 5/9 of the total muffins, the number of muffins left is 8.
How many muffins are left?Given the data in the question, let 'x' represent the total muffins.
Total muffins = xAmount carried away = 105/9 of all of total muffins = 10Number of muffins left = ?First we determine the total amount of muffins 'x'.
5/9 of all of total muffins = 10
5/9 × x = 10
5x/9 = 10
5x = 90
x = 90/5
x = 18
Total amount of muffins was 18.
Now,
Amount of muffins left = Total muffins - Amount carried away
Amount of muffins left = 18 - 10
Amount of muffins left = 8
Given that a colony of ants carried away 10 of your muffins which was 5/9 of the total muffins, the number of muffins left is 8.
Learn more word problems here: brainly.com/question/2610134
#SPJ1
Find the average rate of change for the interval [-4, 0] for the function below
Answer Choices
A. 3/4
B. -4/3
C. 4/3
D. -3/4
![Find the average rate of change for the interval [-4, 0] for the function below Answer Choices A. 3/4](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/HD4Dovozejh2uSkHDsA5NC8xVrwsNbuG.png)
Answers
Answer:
The average rate of change of the function for the interval [-4, 0] is \(\frac{3}{4}\) ⇒ A
Step-by-step explanation:
The average rate of change of the function is the slope of the line that represents the function, m = Δy/Δx, where
Δx = (x2 - x1)Δy = (y2 - y1)From the given figure
→ The values of x in the interval [-4, 0] are -4 and 0
∵ The point (-4, 0) and (0, 3) lie on the line
∴ x1 = -4 and x2 = 0
∴ x2 = 0 and y2 = 3
∵ Δx = 0 - (-4) = 0 + 4 = 4
∵ Δy = 3 - 0 = 3
→ By using the rule of the slope above
∴ m = \(\frac{3}{4}\)
∵ The average rate of change of the function = the slope of the line
∴ The average rate of change of the function for the interval [-4, 0] is \(\frac{3}{4}\)
y is inversely proportional to the square root of (x +4). When x = 5, y = 2. Find y when x = 77.

Answers
Answer:
y = \(\frac{2}{3}\)
Step-by-step explanation:
given y is inversely proportional to \(\sqrt{x+4}\) , then the equation relating them is
y = \(\frac{k}{\sqrt{x+4} }\) ← k is the constant of proportionality
to find k use the condition when x = 5, y = 2
2 = \(\frac{k}{\sqrt{5+4} }\) = \(\frac{k}{\sqrt{9} }\) = \(\frac{k}{3}\) ( multiply both sides by 3 )
6 = k
y = \(\frac{6}{\sqrt{x+4} }\) ← equation of proportion
when x = 77 , then
y = \(\frac{6}{\sqrt{77+4} }\) = \(\frac{6}{\sqrt{81} }\) = \(\frac{6}{9}\) = \(\frac{2}{3}\)
The most appropriate choice for proportionality will be given by - When x = 77, y = 6
What is proportionality?
Suppose there are two quantities. Proportionality indicates that if there is a change in the value of one quantity, the value of other quantity also changes but maintaining a constant ratio Proportionality can be direct or inverse Direct proportion. Two quantities are said to be in direct proportion if on increasing the value of one quantity, the value of other quantity also increases and vice versa.
For example cost of a commodity and quantity of a commodity are in direct proportion Inverse proportion Two quantities are said to be in inverse proportion if on increasing the value of one quantity, the value of other quantity decreases and vice versa.
For example Number of men and number of days taken by those men to complete a job.
Here, y is inversely proportional to \(\sqrt{x+4}\)
So, \(y = k\sqrt{x+4}\) where k is a constant known as constant of proportionality
When x = 2, y = 5Putting the value one quantity, the value of other quantity decreases and vice versa.
For example Number of men and number of days taken by those men to complete a job.
Here, y is inversely proportional to \(\sqrt{x+4}\)
So, \(y = k\sqrt{x+4}\) where k is a constant known as constant of proportionality
When x = 2, y = 5
Putting the value of x and y in the above equation,
\(2 = k\sqrt{5+4}\\2 = k\sqrt{9}\\3k = 2\\k = \frac{2}{3}\)
So,\(y = \frac{2}{3}\sqrt{x+ 4}\)
When x = 77
\(y = \frac{2}{3}\sqrt{77+4}\\y = \frac{2}{3}\sqrt{81}\\y = \frac{2}{3} \times 9\\y = 6\).
To learn more about proportion, refer to the link:
https://brainly.com/question/24868934
#SPJ2
FIND THE VALUE IF X.I REALLY NEED THIS OEN

Answers
The value of x in the given figure of parallel lines is x = 0.89.
What are alternate interior angles?When two parallel lines are sliced by a transversal, alternating interior angles and alternate exterior angles result in the shape "Z".
From the figure we observe that according to alternate interior angle, the angle adjacent to x + 94 is 95x.
Thus, the two angles form a straight line.
The angle of a straight line is 180 degrees.
Thus,
x + 94 + 95x = 180
96x + 94 = 180
x = 0.89
Hence, the value of x in the given figure of parallel lines is x = 0.89.
Learn more about alternate interior angles here:
https://brainly.com/question/28380652
#SPJ1
A basketball player scored 50 points during last nights game all two point and three point baskets the total number of basktes made was 17 how many of each type of basket did they make ?
Answers
The two point baskets are 16 and the three point basket is 1.
What is a linear system of equations?A system of linear equations consists of two or more equations made up of two or more variables such that all equations in the system are considered simultaneously. The solution to a system of linear equations in two variables is any ordered pair that satisfies each equation independently.
Given that, a basketball player scored 50 points.
Let the two point baskets be x and the three point baskets be y.
The total number of baskets made was 17.
Here, x+y=17 -------(i)
During last nights game all two point and three point baskets.
Now, 2x+3y=50 -------(ii)
Substitute x=17-y in the equation (ii), we get
2(17-y)+3y=50
34-2y+3y=50
y=16
Substitute y=16 in equation (i), we get
x=1
Therefore, the two point baskets are 16 and the three point basket is 1.
To learn more about the linear system of an equations visit:
https://brainly.com/question/27664510.
#SPJ9
PLS ADD EXPLANATION
Cylinder radius is 2 cm height is 10cm what is the surface area
Answers
Answer:
150.83 (cm²).
Step-by-step explanation:
1) the area of the bottom and top is: A₁=π*r²*2=2*3.1415*4≈25.13 (cm²);
2) the length of the circle in the bottom/top side is: l=2*π*r=2*3.1415*8≈12.57 (cm);
3) the area of the side surface of the cylinder is: A₂=l*h=12.57*10=125.7 (cm²);
4) the required area of the cylinder is:
A=A₁+A₂=25.13+125.7=150.83 (cm²).
A line passes through (1, 3) and (4, 7). Which line would be perpendicular to this line?
a) y=-x+5
b) y=-x-2
c) y= 4x + 2
d) y=-4x-4
Answers
Answer: Any line with slope of -3/4
Reason:
Let's calculate the slope of the line through those two points
\((x_1,y_1) = (1,3) \text{ and } (x_2,y_2) = (4,7)\\\\m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}\\\\m = \frac{7 - 3}{4 - 1}\\\\m = \frac{4}{3}\\\\\)
The slope of the line is 4/3
Anything perpendicular to this has a slope of -3/4. I flipped the fraction and flipped the sign (from positive to negative).
So for example, the answer may be something like \(y = -\frac{3}{4}x+5\) or \(y = -\frac{3}{4}x-2\). All that matters is the -3/4 out front of the x.
Side note: the original slope 4/3 and perpendicular slope -3/4 multiply to -1
What is the maximum number of turns in the graph of this function? f(x) = x5 – x2 – x+1
Answers
Answer:
4
Step-by-step explanation:
how to determine if a relation is a function calculator
Answers
Answer:
A relation is defined as the collection of inputs and outputs which are related to each other in some way. In case, if each input in relation has accurately one output, then the relation is called a function.
Based on the given relation, we found that it is not a function because it has repeating x-values. Remember, for a relation to be a function, each input (x-value) must correspond to exactly one output (y-value).
To determine if a relation is a function, you need to check if each input (x-value) corresponds to exactly one output (y-value). You can use the following steps:
1. Identify the given relation as a set of ordered pairs, where each ordered pair represents an input-output pair.
2. Check if there are any repeating x-values in the relation. If there are no repeating x-values, move to the next step. If there are repeating x-values, the relation is not a function.
3. For each unique x-value, check if there is only one corresponding y-value. If there is exactly one y-value for each x-value, then the relation is a function. If there is more than one y-value for any x-value, then the relation is not a function.
Let's consider an example relation: {(1, 2), (2, 3), (3, 4), (2, 5)}.
Step 1: Identify the relation as a set of ordered pairs: {(1, 2), (2, 3), (3, 4), (2, 5)}.
Step 2: Check for repeating x-values. In our example, we have a repeating x-value of 2. Therefore, the relation is not a function.
To know more about Relation, visit
https://brainly.com/question/30056459
#SPJ11
find area of the figure

Answers
Answer:
70 sq. in
Step-by-step explanation:
Area of the figure
= ( 10 x 5 ) + ( 5 x 4 )
= 50 + 20
= 70
= 70 sq. in
Give a recursive definition of: a. The set of strings {1, 11, 111, 1111, 11111, ....} b. The function f (n) = n + 1/3, n = 1, 2, 3, ...
Answers
a. The set of strings {1, 11, 111, 1111, 11111, ....} can be defined recursively as follows:
- Base case: S(1) = "1"
- Recursive step: S(n) = S(n-1) + "1", for n > 1
b. The function f(n) = n + 1/3, n = 1, 2, 3, ... can be defined recursive as:
- Base case: f(1) = 1 + 1/3
- Recursive step: f(n) = f(n-1) + 1, for n > 1
Recursion is the process of calling itself. This process provides a way to break complex problems into simpler processes that are easier to solve. Recursion can be a bit confusing. The best way to determine how it works is to experiment with it.
a. The recursive definition of the set of strings {1, 11, 111, 1111, 11111, ....} is as follows:
- The base case is the string "1".
- For any string in the set, we can obtain the next string by appending another "1" to the end. In other words, if s is a string in the set, then s + "1" is also in the set.
b. The recursive definition of the function f(n) = n + 1/3, n = 1, 2, 3, ... is as follows:
- The base case is f(1) = 4/3.
- For any n > 1, we can obtain f(n) by adding 1/3 to f(n-1). In other words, f(n) = f(n-1) + 1/3.
Learn more about Function:
brainly.com/question/12431044
#SPJ11
Which expression converts 45° to radians? 45 degrees times 180 degrees 45 degrees times StartFraction 180 degrees Over pi EndFraction 45 degrees times StartFraction pi Over 180 degrees EndFraction 45 degrees times pi.
Answers
One short cut to remember how the solution is found, remember that degree unit must be removed and radian has to come(to convert from degree to radian) and that will be removed only when division by degree will happen and multiplication by something in radian.
The correct expression that converts 45° to radian is given by:
Option C: \(45^\circ \times \dfrac{\pi^c}{180^\circ}\)
Both measure angles. Remember the fact that one full rotation is 360° or \(2\pi^c\) (this superscript c denotes that angle is in radians).
pi is 3.14159... and pi radians means 3.14.. radians which measures half of full rotation(since 2 times pi measures full rotation).
Thus, we have:
\(360^\circ = 2\pi^c\\\\ \text{Dividing by 360 on both sides}\\\\ 1^\circ = \dfrac{2\pi^c}{360}\\\\ 1^\circ = \dfrac{\pi^c}{180}\)
Thus, we have:
\(45^\circ = 45 \times 1^\circ = 45 \dfrac{\pi^c}{180} = \dfrac{45^\circ\pi^c}{180^\circ}\\ \)
Thus, the correct expression that converts 45° to radian is given by:
Option C: \(45^\circ \times \dfrac{\pi^c}{180^\circ}\)
Learn more about degree and radian here:
https://brainly.com/question/11521023
Answer:
Option C
Step-by-step explanation:
Got it right on edge
how do you solve it?
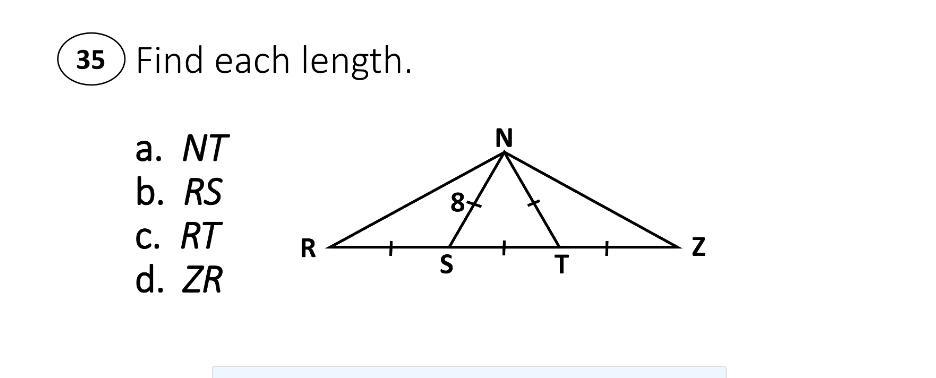
Answers
9514 1404 393
Answer:
a) NT = 8
b) RS = 8
c) RT = 16
d) ZR = 24
Step-by-step explanation:
All of the marked sides are congruent. (That's what the marks mean.) It might help you to put 8 next to each hash mark like it is on NS. So, you have ...
NT = RS = ST = TZ = NS = 8
Segments on the same line sum, so ...
RT = RS +ST = 2RS = 16
ZR = RS +ST +TZ = 3RS = 24
a) NT = 8
b) RS = 8
c) RT = 16
d) ZR = 24
Please answer this question correctly thank you

Answers
Step-by-step explanation:
9% of 200 = 1840% of 120 = 4845% of 90 = 40.5Which expression is equivalent to 27
?

Answers
Answer:
Last one
Step-by-step explanation:
3^4*3^-7
Multiply the polynomials (3x+4)(5x+1)
Answers
Answer:
15x^2 + 23x + 4
Step-by-step explanation:
(3x+4)(5x+1)
You put them around a square, like in the picture.
You then cross multiply them.
After that, add all the numbers together.
Hope this helped!

The chance of solving a problem by A and B is and 1/3 and 2/5 respectively. What is the probability the problem will be solved?
a)2/15
b)1
c)9/15
d)11/15
Books shows "c" as the answer.. I am confused..
Answers
We want to compute the probability P(A or B) because we could either solve it following path A, path B, or doing both paths.
P(A) = 1/3
P(B) = 2/5
P(A and B) = P(A)*P(B) assuming A,B are independent
P(A and B) = (1/3)*(2/5)
P(A and B) = 2/15
--------
P(A or B) = P(A) + P(B) - P(A and B)
P(A or B) = 1/3 + 2/5 - 2/15
P(A or B) = 5/15 + 6/15 - 2/15
P(A or B) = (5 + 6 - 2)/15
P(A or B) = 9/15
We could reduce this to 3/5, but it appears your teacher has chosen not to.
Jennifer made these measurements on ABC,BC must be-?

Answers
Answer:
between 10 and 12
Step-by-step explanation:
Given the measure of angles:
m∠B = 70°
m∠C = 60°
m∠A = 50°
We know m∠B = 70° because the sum of interior angles in a triangle is equal to 180°.Following this information, since the side lengths are directly proportional to the angle measure they see:
Angle B is the largest angle. Therefore, side AC is the longest side of the triangle since it is opposite of the largest angle.
Angle C is the smallest angle, so the side AB is the shortest side.
Therefore, side BC must be between 10 and 12 inches.
(3x+1)^ 2-(3x+1)(3x+5)+(3x+5)^
Answers
Answer:
1-9×
Step-by-step explanation:
its ur choice if ur gonna copy my ans
Evaluate 2-(-4) + (-g) where y= 7.
Answers
Answer:
-1Step-by-step explanation:
2 - (-4) + (-y)
Substitute y = 7 to the expression:
2 - (-4) + (-7) = 2 + 4 - 7 = 6 - 7 = -1
in the diagram, AB= BC. Prove that ABCD is a cyclic quadrilateral. Give reasons for any statements you make

Answers
Answer:
Step-by-step explanation:
Given : AB = BC.
To Prove : ABCD is a cyclic quadrilateral.
Solution : AB ≅ CD [Given]
m∠BAC = m∠BCA = x° [Property of an isosceles triangle]
m∠ABC = 180° - (m∠BAC + m∠ACB) [Triangular sum theorem]
m∠ABC = 180° - (x + x)
= 180° - 2x°
m∠ABC + m∠ADC = (180 - 2x) + 2x
= 180°
[Property of cyclic quadrilateral → Sum of opposite angles = 180°]
Hence proved.
Berto has $12 to put gas in his car. If gas costs $3.75 per gallon, which ordered pair relating number of gallons of gas, x, to the total cost of the gas, y, includes the greatest amount of gas Berto can buy?
(__,__ )
Answers
Answer:
If gas costs $3.75 per gallon and Berto has $12, then he can purchase 12/3.75 gallons. This is approximately 3.2 gallons. So the coordinate on this line would be (3.2, 12).
Actually... It's from web
21 m
15 m
Which is closest to the length of XY?

Answers
Answer:
18.0 i think
Step-by-step explanation:
True or False
A solution to 8 = -x + 10 is 2
Answers
Answer:
\(\huge\underline{Answer - }\)
\(\bold{8 = - x + 10} \\ \\ \bold{\implies \: - x = 8 - 10} \\ \\ \bold{\implies \: \cancel - x = \cancel - 2 }\\ \\ \bold{\implies x\: = 2}\)
hence , the given statement is true !
hope helpful ~
Answer:
TrueStep-by-step explanation:
So, Lets find out if the solution is true or not, So first let us find the value of x.
⇒ 8 = -x + 10
We can rewrite the equation as,
⇒ -x + 10 = 8
Subtracting 10 from both sides we get :
⇒ -x + 10 – 10 = 8 – 10
⇒ -x = -2
Multiplying both sides by (-1) :
⇒ -1(-x) = -1(-2)
⇒ x = 2
Therefore,
The statement "A solution to 8 = -x + 10 is 2" is trueif p = 2-5 and q = 8x3 find 3p-q
Answers
Answer:
3p - q = 3(2-5) - (8x3) = -9 - 24 = -33. Therefore, 3p-q=-33.
Alana and her classmates placed colored blocks on a scale during a science lab. The green block weighed 9 pounds and the purple block weighed 0.77 pounds. How much more did the green block weigh than the purple block?
Answers
The weight more the green block weigh than the purple block is 8.23 pounds
We are given that;
Weight= 0.77 pounds
Number of blocks= 9
Now,
To find how much more the green block weighed than the purple block, we can subtract the weight of the purple block from the weight of the green block. This is called finding the difference between two numbers. We can write this as:
Difference=Green block−Purple block
Plugging in the given values, we get:
Difference=9−0.77
To subtract these numbers, we need to align the decimal points and subtract each place value from right to left. We can also add a zero after the decimal point in 9 to make it easier to subtract. We get:
−9.000.778.23
Therefore, by algebra the answer will be 8.23 pounds.
More about the Algebra link is given below.
brainly.com/question/953809
#SPJ1