An investment of $600 is made into an account that earns 6. 5% annual simple interest for 15
years. Assuming no other deposits or withdrawals are made, what will be the balance in the
account?
Answers
According to the investment, after 15 years, the balance in the account would be $1185.
To calculate the final balance after 15 years, we can use the formula for simple interest:
Simple Interest = Principal x Interest Rate x Time
In this case, the principal is $600, the interest rate is 6.5%, and the time is 15 years.
Simple Interest = $600 x 0.065 x 15
Simple Interest = $585
So the investment of $600 earns $585 in simple interest over 15 years. To find the final balance, we add the interest earned to the initial investment:
Final Balance = Principal + Simple Interest
Final Balance = $600 + $585
Final Balance = $1185
To know more about investment here
https://brainly.com/question/365124
#SPJ4
Related Questions
consider let f be a differetiable function. what is the best estimate of 11 4 if a trapezoidal sum is used with 3 subintervals?verify
Answers
The best estimate of ∫(4 to 11) f(x) dx using a trapezoidal sum with 3 subintervals can be found by dividing the interval into three equal subintervals and applying the trapezoidal rule.
The trapezoidal rule is a method for approximating the definite integral of a function over an interval. It involves dividing the interval into subintervals and approximating the area under the curve by the sum of trapezoids formed between adjacent points.
In this case, we are given the interval from 4 to 11 and want to estimate the integral of f(x) over this interval using a trapezoidal sum with 3 subintervals. To do this, we divide the interval into three equal subintervals: [4, 6], [6, 8], and [8, 11]. Then, we apply the trapezoidal rule to each subinterval and sum up the results.
The trapezoidal rule states that the area under each subinterval can be approximated as (b-a) * (f(a) + f(b)) / 2, where a and b are the endpoints of the subinterval.
By applying the trapezoidal rule to each subinterval and summing the results, we obtain the best estimate of the integral.
To learn more about trapezoidal rule visit:
brainly.com/question/30401353
#SPJ11
Write a rule for g described by the transformations of the graph of f.
Let g be a horizontal shrink by a factor of 3/7, followed by a translation 5 units left
of the graph of f(x)=(21x)^1/2
Answers
Answer:\(g(x)=\frac{3}{7}(21(x+5))^{1/2}\)
Step-by-step explanation:
Transformation rule:
Shifting by k units left : \(f(x)\to f(x+5)\)
Dilation by a factor of h units: \(f(x)\to hf(x)\)
Let g be a horizontal shrink by a factor of 3/7, followed by a translation 5 units left of the graph of \(f(x)=(21x)^{1/2}\)
The rule for g described by the transformations of the graph of f. : \(g(x)=\frac{3}{7}(21(x+5))^{1/2}\)
Find the GCF from the two numbers, and rewrite the sum using the distributive property.
18-12=.
Answers
Answer:
ab+ac=a(b+c)
where a is the greatest common factor
find gcf of each
factor each
18=2*3*3
12=2*2*3
GCF=2*3=6
so
18+12=6(3)+6(2)=6(3+2)
Step-by-step explanation:
find the radius of convergence and interval of convergence of the series. [infinity] xn 9 7n! n = 1
Answers
The radius of convergence and interval of convergence of the series, [infinity] xn / 9^(7n!) n = 1, is R = ∞.
To determine the radius of convergence and interval of convergence of the series, [infinity] xn / 9^(7n!) n = 1, we shall apply the ratio test.
Firstly, let's write down the series to be tested with the general term written explicitly.
[infinity] xn / 9^(7n!) n
= 1x_n
= x_n9^(7n!)x_(n+1)
= x_(n+1)9^(7(n+1)!)
Thus, we can write out the ratio as: |x_(n+1)|9^(7(n+1)!)|x_n|9^(7n!)
The above equation is only valid when n is sufficiently large. This is because for n < N (N some positive integer), the values of the ratio test might be undefined (or meaningless) for one reason or another.
To make the calculation of the ratio easier, we shall take the absolute value of each term in the above equation.
Hence, |x_(n+1)| / |x_n| = 9^(7n! - 7(n+1)!)
Now we are able to find the radius of convergence. The ratio test tells us that a series is convergent if the ratio of successive terms approaches zero as n approaches infinity.
We can write this mathematically as: lim_(n->∞) |x_(n+1)| / |x_n| < 1
For the series given in this question, this condition is equivalent to: lim_(n->∞) 9^(7n! - 7(n+1)!) < 1
Simplifying, we get: lim_(n->∞) 9^(-7n!) / 9^(-7(n+1)!) < 1lim_(n->∞) 1 / 9^7 < 1
Since the limit is less than 1, the series is convergent.
The radius of convergence is: R = ∞
Interval of convergence can be obtained from the formula: [-R, R].
Therefore, interval of convergence of the series is (-∞, ∞).
Know more about the radius of convergence
https://brainly.com/question/17019250
#SPJ11
For my higher grade and i dint get this problem

Answers
Answer:
y = 9
Step-by-step explanation:
\(\frac{2}{6}\) = \(\frac{y}{27}\) ( cross- multiply )
6y = 2 × 27 = 54 ( divide both sides by 6 )
y = 9
Answer:
Step-by-step explanation: From the question 2/6 = y/ 27
Cross multiply
It becomes 2 * 27 = 6 * y
54 = 6y
Make y the subject
y = 54/ 6
y = 9
A restaurant would like to estimate the proportion of tips that exceed 18% of its dinner bills. Without any knowledge of the population proportion, determine the sample size needed to construct a 96% confidence interval with a margin of error of no more than 7% to estimate the proportion. The sample size needed is _____
Answers
The sample size needed is 103.
A restaurant would like to estimate the proportion of tips that exceed 18% of its dinner billsThe sample size needed to construct a 96% confidence interval with a margin of error of no more than 7% to estimate the proportion of tips is given by : \[n=\frac{{z}^{2}p(1-p)}{E^{2}}\] where, n is the sample size, z is the z-score, p is the population proportion, and E is the margin of errorA confidence interval provides an estimated range of values that’s likely to include an unknown population parameter, the estimated range being calculated from a given set of sample dataThe higher the confidence level required, the larger the sample size will be, which leads to narrower confidence intervalsA margin of error is a statistic expressing the amount of random sampling error in a survey's results. The larger the margin of error, the less confidence one should have that the poll's reported results are close to the true figures.Therefore, the sample size needed to construct a 96% confidence interval with a margin of error of no more than 7% to estimate the proportion, without any knowledge of the population proportion, to estimate the proportion of tips that exceed 18% of its dinner bills is 103.
To know more about simple random sampling, visit the link : https://brainly.com/question/13219833
#SPJ11
the diameter of a circle is 9 in . find its area to the nearest tenth.
Answers
Answer:
63.6
Step-by-step explanation:
diameter = 9
radius = 9/2= 4.5
Area of circle = 22/7 × radius²
so,
22/7×4.5×4.5 = 63.6428571
if we round off it to nearest tenth it will be = 63.6
Find the root of
\( \sqrt{2x { }^{2} } + x + \sqrt{2} = 0\)
Answers
Answer:
The root of x = -2 + √2
Step-by-step explanation:
Step(i):-
Given \(\sqrt{2x^{2} } + x +\sqrt{2} = 0\)
⇒ \(\sqrt{2} } ( x^2 ) ^{\frac{1}{2} } + x +\sqrt{2} = 0\)
⇒ \(\sqrt{2}x + x +\sqrt{2} = 0\)
⇒ \((\sqrt{2} + 1) x = - \sqrt{2}\)
\(x = \frac{-\sqrt{2} }{(\sqrt{2} + 1)}\)
Step(ii):-
Rationalizing
\(x = \frac{-\sqrt{2} }{(\sqrt{2} + 1)} X \frac{(\sqrt{2} - 1)}{(\sqrt{2} - 1)}\)
Apply ( a-b ) ( a+b) = a²-b²
\(x = \frac{-\sqrt{2}(\sqrt{2} -1) }{(\sqrt{2})^{2} - 1^{2} )} = \frac{-(2-\sqrt{2} }{2-1}\)
The root of x = -2 + √2
A rectangular piece of plywood 4 ft by 5.5 ft is cut from one corner to the opposite corner. What are the angles between the edges of the resulting pieces
Answers
The angles between the edges of the resulting pieces are approximately \($56.1^\circ$ and $42.5^\circ$.\)
We know that the rectangle has sides of length 4 ft and 5.5 ft, so we can use the Pythagorean Theorem to find the length of the diagonal \($BD$\):
\($$ BD^2 = 4^2 + 5.5^2 $$\)
\($$ BD^2 = 16 + 30.25 $$\)
\($$ BD^2 = 46.25 $$\)
\($$ BD = \sqrt{46.25} $$\)
\($$ BD = 6.8 \text{ ft (rounded to one decimal place)} $$\)
Now, we can use the Law of Cosines to find the angle between sides \($AB$\)and \($AD$\) in triangle \($ABD$\):
\($$ \cos(A) = \frac{BD^2 + AB^2 - AD^2}{2 \cdot BD \cdot AB} $$\)
\($$ \cos(A) = \frac{6.8^2 + 4^2 - 5.5^2}{2 \cdot 6.8 \cdot 4} $$\)
\($$ \cos(A) = 0.5471 $$\)
\($$ A = \cos^{-1}(0.5471) $$\)
\($$ A = 56.1^\circ \text{ (rounded to one decimal place)} $$\)
Similarly, we can use the Law of Cosines to find the angle between sides \($BC$\) and \($CD$\) in triangle:
\($$ \cos(B) = \frac{BD^2 + BC^2 - CD^2}{2 \cdot BD \cdot BC} $$\)
\($$ \cos(B) = \frac{6.8^2 + 5.5^2 - 4^2}{2 \cdot 6.8 \cdot 5.5} $$\)
\($$ \cos(B) = 0.7416 $$\)
\($$ B = \cos^{-1}(0.7416) $$\)
\($$ B = 42.5^\circ \text{ (rounded to one decimal place)} $$\)
Therefore, the angles between the edges of the resulting pieces are approximately \($56.1^\circ$ and $42.5^\circ$.\)
To learn more about Angles refer here:
https://brainly.com/question/7116550
#SPJ11
given the following measures of the side of triangles, which is a right triangle?

Answers
Answer:
Step-by-step explanation:
Essentially, we can use the pythagorean rule that:
a^2+b^2=c^2
c^2 resembles the hypotenuse, which is almost always the largest number. therefore, we simply have to find two which equal the largest side:
9^2+40^2=41^2
81+1600=1681
1681=1681
Based on this math, A is our right angle!
Hope this helps!
If a vector makes an angle of 295∘ counterclockwise with the positive x-axis, then the sign of the x-component and the y component of this vector will be, respectively negative, negative positive, positive positive, negative negative, positive -/2 Points] A vector A has an x component of 4m and a y component of 8 m. (a) Calculate the magnitude of vector A. m (b) Calculate the angle that vector A makes with the positive x-axis. Enter your answer correct to 3 significant figures.
Answers
The sign of the x-component and y-component of the vector will be negative and positive, respectively. The magnitude of vector A is approximately 8.944m, and the angle it makes with the positive x-axis is approximately 63.43 degrees.
(a) To calculate the magnitude of vector A with x-component 4m and y-component 8m, we can use the Pythagorean theorem. The magnitude (|A|) is given by the square root of the sum of the squares of the components: |A| = √(4^2 + 8^2) = √(16 + 64) = √80 ≈ 8.944m.
(b) To calculate the angle that vector A makes with the positive x-axis, we can use the inverse tangent function. The angle (θ) is given by the arctangent of the ratio of the y-component to the x-component: θ = tan^(-1)(8/4) ≈ 63.43 degrees.
In summary, the magnitude of vector A is approximately 8.944m, and the angle it makes with the positive x-axis is approximately 63.43 degrees.
Learn more about vector here:
https://brainly.com/question/24256726
#SPJ11
Golving Linear Equation Application Problems
Content attribution
Use a Formula to Solve a Real World Application
Question
On Saturday morning, it took Jennifer 3.6 hours to drive to her mother's house for the weekend. On Sunday evening, due to
heavy traffic, it took Jennifer 4 hours to return home. Her speed was 5 mi/hr slower on Sunday than on Saturday. What was
her speed on Sunday? Do not include units in your answer.
Provide your answer below:
FEEDBACK
Answers
Answer:
Speed of Jennifer on Sunday \(=45\) mi/hr
Step-by-step explanation:
Let speed of Jennifer on Saturday be x mi/hr
On Saturday morning, it took Jennifer 3.6 hours to drive to her mother's house for the weekend.
Distance travelled by Jennifer on Saturday = Speed × Time \(=3.6x\) miles
Speed of Jennifer on Sunday = \((x-5)\) mi/hr
On Sunday evening, due to heavy traffic, it took Jennifer 4 hours to return home.
Distance travelled by Jennifer on Sunday = Speed × Time \(=4(x-5)\) miles
As distance is obviously same on both Saturday and Sunday,
\(3.6x=4(x-5)\\3.6x=4x-20\\20=4x-3.6x\\20=0.4x\\x=\frac{20}{0.4}\\ x=50\)
Therefore,
Speed of Jennifer on Sunday = \((50-5)=45\) mi/hr
What is the area of the square adjacent to the third side of the triangle?
If known could u answer the other as well ?

Answers
Answer:
85 units^2 = Area of Blue Square
and
x = 5 units
Step-by-step explanation:
To do this we use the Pythagorean theorem (a^2 + b^2 = c^2). a and b represent the legs of the triangle whereas c represents the longest side of the triangle, or the hypotenuse.
Since we know the area of a square is the side length multiplied by itself (or the side length squared), \(\sqrt{35}\) is the side length of the pink square and \(\sqrt{50}\) is the side length of the green square.
That means a = \(\sqrt{35}\) and b = \(\sqrt{50}\) , so...
\((\sqrt{35} )^{2} + (\sqrt{50})^{2} = c^{2}\)
35 + 50 = c^2
85 = c^2
\(\sqrt{85} = c\)
Now we need to square the square root of 85 to find the area of the blue square.
\((\sqrt{85})^{2} = Area of blue square\)
85 units^2 = Area of Blue Square
To solve the other question we use the same formula again.
\(x^2 + 12^2 = 13^2\\x^2 +144 = 169\\-144\\x^2 = 25\\x=\sqrt{25} \\x=5\)
x = 5 units
Show that if m
∗
(A)=0, then m
∗
(AUB)=m
∗
(B)
Answers
A and B have the same elements, the measure of AUB will be equal to the measure of B.
To show that if m*(A) = 0, then m*(AUB) = m*(B), we need to prove the following:
1. If m*(A) = 0, then A is a null set.
2. If A is a null set, then AUB = B.
3. If AUB = B, then m*(AUB) = m*(B).
Let's break down each step:
1. If m*(A) = 0, then A is a null set:
- By definition, a null set has a measure of 0.
- Since m*(A) = 0, it implies that A has no elements or its measure is 0.
- Therefore, A is a null set.
2. If A is a null set, then AUB = B:
- Since A is a null set, it means that it has no elements or its measure is 0.
- In set theory, the union of a null set (A) with any set (B) results in B.
- Therefore, AUB = B.
3. If AUB = B, then m*(AUB) = m*(B):
- Since AUB = B, it implies that both sets have the same elements.
- The measure of a set is defined as the sum of the measures of its individual elements.
- Since A and B have the same elements, the measure of AUB will be equal to the measure of B.
- Therefore, m*(AUB) = m*(B).
By proving these three steps, we have shown that if m*(A) = 0, then m*(AUB) = m*(B).
To know more about measure, visit:
https://brainly.com/question/28913275
#SPJ11
in a standard deck of cards, what is the probability of drawing a face card followed by drawing a non-face card? answer choices are in the form of a percentage, rounded to the nearest whole number.
Answers
The probability of drawing a face card followed by condition of drawing non face card is equal to 18% ( approximately).
In a standard deck of cards,
There are 12 face cards 4 jacks, 4 queens, and 4 kings
And 40 non-face cards 10 numbered cards each for the 4 suits.
The probability of drawing a face card on the first draw is
= 12/52
= 3/13.
Assuming a face card was drawn on the first draw,
There are now 51 cards remaining in the deck.
Of which 40 are non-face cards.
Probability of drawing a non-face card on the second draw is
= 40/51.
Probability of both events happening drawing a face card followed by a non-face card
= Multiply the probabilities of the individual events
= (3/13) x (40/51)
= 120/663
= 0.181approximately
= 18% (rounded to the nearest whole number).
Therefore, the probability of drawing a face card followed by drawing a non-face card in a standard deck of cards is approximately 18%.
Learn more about probability here
brainly.com/question/28326750
#SPJ4
Discrete Random Variables
Answers
A discrete random variable may take on only a countable number of distinct values such as 0,1,2,3,4,...
Discrete random variables are usually (but not necessarily) counts. If a random variable can take only a finite number of distinct values, then it must be discrete. Examples of discrete random variables include the number of children in a family, the Friday night attendance at a cinema, the number of patients in a doctor's surgery, and the number of defective light bulbs in a box of ten.
The probability distribution of a discrete random variable is a list of probabilities associated with each of its possible values. It is also sometimes called the probability function or the probability mass function.
Example'
The cumulative distribution function for the above probability distribution is calculated as follows:
The probability that \(X\) is less than or equal to is 0.1,
the probability that \(X\) is less than or equal to 2 is 0.1+0.3 = 0.4,
the probability that \(X\) is less than or equal to 3 is 0.1+0.3+0.4 = 0.8, and
the probability that \(X\) is less than or equal to 4 is 0.1+0.3+0.4+0.2 = 1.
To learn more about cumulative distribution, visit
brainly.com/question/19884447
#SPJ4
find the critical value za/2 needed to construct a confidence interval with level 82%. round the answer to two decimal places.
Answers
Using the z table, the critical value \(z_{a/2}\) needed to construct a confidence interval with level 82% is 1.34.
In the given question,
We have to find the critical value \(z_{a/2}\) needed to construct a confidence interval with level 82%.
The confidence interval is 82%.
We can write 82% as 82/100 and 0.82.
Now the value of
\(\alpha\)=1−0.82
\(\alpha\)=0.18
Now finding the value of \(\alpha\)/2
\(\alpha\)/2=0.18/2
\(\alpha\)/2=0.09
Now finding the value of \(z_{a/2}\).
\(z_{0.82}\) = 1.34
Hence, the critical value \(z_{a/2}\) needed to construct a confidence interval with level 82% is 1.34.
To learn more about standard normal random variable link is here
brainly.com/question/14782203
#SPJ4
Look at the pattern below.
8, 17, 26, 35, 44, …
Which expression represents this pattern algebraically?
A: n+ 9
B: n - 9
C: 9n +1
D: 9n - 1
Answers
The pattern for the sequence 8, 17, 26, 35, 44, … is 9n - 1
Calculating the pattern for the expressionThe pattern in the question is given as
8, 17, 26, 35, 44, …
In the above expressions and pattern, we can see that
The current term is added to 9 to get the next term
From the above, we have the following
First term, a = 8Common difference, d = 9This means that the pattern is an arithmetic sequence with the following features
a = 8
d = 9
An arithmetic sequence is represented as
f(n) = a + (n - 1)d
When the values of "a" and "d" are substituted in the above equation, we have the pattern to be
f(n) = 8 + (n - 1)9
So, we have
f(n) = 8 + 9n - 9
Evaluate
f(n) = 9n - 1
Hence, the pattern for the sequence is 9n - 1
Read more about sequence at
brainly.com/question/6561461
#SPJ1
Topic: Determining if given values are solutions to a two variable equation

Answers
Answer:
2. a & c
3. a, b & c
Step-by-step explanation:
Substitute each solutions to the question to see if you get the answer
a. 5(2)-0=10 -- so (2,0) is the solution
b. 5(3)-0=15 -- (3,0) is not the solution
c. 5(0)-(-10)=10 -- (0,-10) is the solution
d. 5(1)-(1)=4 -- (1,1) is not the solution
a. -(-4)+ 6(1) = 10 -- so (-4,1) is the solution
b. -(-22)+ 6(-2) = 10 -- so (-22,-2) is the solution
c. -(2)+ 6(2) = 10 -- so (2,2) is the solution
d. -(10)+ 6(0) = - 10 -- so (10,0) is not the solution
help pls ill give brainlest

Answers
But in simplest form I’m pretty sure it’s 1/7
which of the following statistics determines whether there are differences between two nominally scaled variables?
Answers
The chi-square statistic is used to determine whether there are differences between two nominally scaled variables. Chi-Square is a statistical test used to compare two nominal variables to determine whether they differ.
The Chi-Square test is used to test for differences between two groups. When you want to compare groups or examine the relationship between two variables, this test is useful. The chi-square test is a method of statistical inference that can be used to compare observed frequencies with expected frequencies, allowing us to determine whether there is a meaningful difference between them. When the p-value obtained from a chi-square test is less than 0.05, it is generally considered statistically significant.
Learn more about Chi-Square
https://brainly.com/question/32595988
#SPJ11
6] A ship sails 70 km on a bearing of 38° and then changes course and sails 40 km on
a bearing of 150° By making a scale diagram find: -
a) The final distance of the port from the ship.
b) The final bearing of the port from the ship.
Answers
The final distance of the port from the ship is 75.63 km and the final bearing of the port from the ship is 263.57° using cosine and sine rules.
How to evaluate for the final distance and bearingConsidering the triangle formed by the ship ∆ABC where A, B and C are the points for; the port, where the ship changes its course, and its final bearing. The final distance "a" of the port from the ship is calculated with cosine rule as follows;
a² = b² + c² - 2(b)(c)cosA
a² = 40² + 70² - 2(40)(70)cos82°
a² = 1600 + 4900 - 5600cos82°
a² = 5720.63 {take square root of both sides}
a = 75.63
For the triangle ABC, by sine rule;
a/sinA = b/sinB = c/sinC
75.63/sin82° = 70/sinC
C = sin⁻¹(70 × sin82°/75.63) {by cross multiplication}
C = 66.43
angle C = 60 + 6.43 {60° is an alternate angle with angle 30° at the point B where the ship chenged course and 6.43° is a complementary angle at the 3rd quadrant of point C}
The final bearing of the port from the ship is calculated as;
180° + (90 - 6.43)° = 263.57°
Therefore, the final distance of the port from the ship is 75.63 km and the final bearing of the port from the ship is 263.57° using cosine and sine rules.
Know more about bearing here:https://brainly.com/question/22518031
#SPJ1
For triangle ABC. Points M, N are the midpoints of AB and AC respectively. Bn intersects CM at O. Know that the area of triangle MON is 4 square centimeters. Find the area of ABC
Answers
The area of triangle ABC = (40/3) sq.cm.
Given that triangle ABC with midpoints M and N for AB and AC respectively, Bn intersects CM at O and area of triangle MON is 4 square centimeters. To find the area of ABC, we need to use the concept of the midpoint theorem and apply the Area of Triangle Rule.
Solution: By midpoint theorem, we know that MO || BN and NO || BM Also, CM and BN intersect at point O. Therefore, triangles BOC and MON are similar (AA similarity).We know that the area of MON is 4 sq.cm. Then, the ratio of the area of triangle BOC to the area of triangle MON will be in the ratio of the square of their corresponding sides. Let's say BO = x and OC = y, then the area of triangle BOC will be (1/2) * x * y. The ratio of area of triangle BOC to the area of triangle MON is in the ratio of the square of the corresponding sides. Hence,(1/2)xy/4 = (BO/MO)^2 or (BO/MO)^2 = xy/8Also, BM = MC = MA and CN = NA = AN Thus, by the area of triangle rule, area of triangle BOC/area of triangle MON = CO/ON = BO/MO = x/(2/3)MO => CO/ON = x/(2/3)MO Also, BO/MO = (x/(2/3))MO => BO = (2/3)xNow, substitute the value of BO in (BO/MO)^2 = xy/8 equation, we get:(2/3)^2 x^2/MO^2 = xy/8 => MO^2 = (16/9)x^2/ySo, MO/ON = 2/3 => MO = (2/5)CO, then(2/5)CO/ON = 2/3 => CO/ON = 3/5Also, since BM = MC = MA and CN = NA = AN, BO = (2/3)x, CO = (3/5)y and MO = (2/5)x, NO = (3/5)y Now, area of triangle BOC = (1/2) * BO * CO = (1/2) * (2/3)x * (3/5)y = (2/5)xy Similarly, area of triangle MON = (1/2) * MO * NO = (1/2) * (2/5)x * (3/5)y = (3/25)xy Hence, area of triangle BOC/area of triangle MON = (2/5)xy / (3/25)xy = 10/3Now, we know the ratio of area of triangle BOC to the area of triangle MON, which is 10/3, and also we know that the area of triangle MON is 4 sq.cm. Substituting these values in the formula, we get, area of triangle BOC = (10/3)*4 = 40/3 sq.cm. Now, we need to find the area of triangle ABC. We know that the triangles ABC and BOC have the same base BC and also have the same height.
Know more about triangle here:
https://brainly.com/question/29083884
#SPJ11
what is the Recursive Formula and the Explicit Formula for Let a1=2, 9, 16, 23, and Let a1=2, 14, 98, 686, ...
Answers
Answer:
Step-by-step explanation:
I don’t know why they bother teaching recursive formulas as the explicit is almost always used :)
For 2,9,16,23...
Recursive is a(n+1)=an+7
Explicit is an=2+7(n-1)
(or more neatly an=7n-5)
For 2,14,98,686...
Recursive is a(n+1)=7an
Explicit is an=2(7^(n-1))
(or (2/7)7^n )
URGENT! BRAINLIEST ANSWER!
Determine whether the triangles are similar. If they are, write a similarity statement. Explain your reasoning.
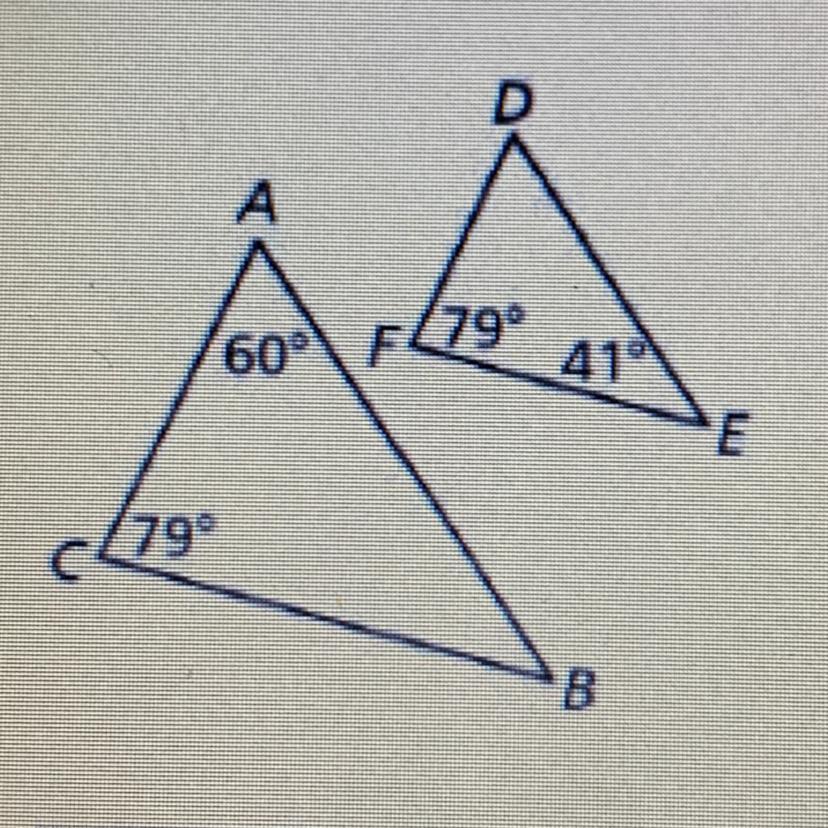
Answers
Answer: Yes, they are similar
Step-by-step explanation:
Angle A is congruent to angle D
Angle B is congruent to angle E
Angle C is congruent to angle F
Therefore, the triangles are similar by the AAA (angle-angle-angle) similarity theorem.
calculate the p-value associated with the null hypothesis that 50% of the students at eastern work more than 10 hours a week.
Answers
The p-value associated with the null hypothesis = 0.05
Fail to reject the null hypothesis. The P-value is greater than the level of significance.
Candice should reject the null hypothesis as the 50% confidence interval does not contain 10 hours
Small p-values offer proof that the null hypothesis is false. The stronger the evidence is against the null hypothesis, the smaller (closer to 0) the p-value. The null hypothesis is rejected if the p-value is less than or equal to the chosen significance level; otherwise, it is not.
You have the Hypothesis that "students study less than 10 hours, on average, per week"
Symbolically:
H₀:μ≥10hours
H₁:μ<10hours
The significant level for this case study is 50% - 0.05. If the results gotten is less than the significance level, we reject the null hypothesis, but if greater, we fail to reject the null hypothesis.
The p-value of 0.05 is one of the most often used numbers. When the calculated p-values are less than 0.05, the faulty hypothesis is considered to be fraudulent or invalid (subsequently the name invalid theory). Additionally, the faulty theory is taken into consideration to be clear if the value is greater than 0.05.
The edge for that likelihood in our model is 0.05, and it represents the probability that our results will be similar to the invalid speculation. Therefore, if the calculated p-value is less than 0.05, it actually means that there is a very little likelihood that we would have the same results as the flawed hypothesis. Additionally, if the p-value is greater than 0.05, there is a very strong probability that the results will be similar to the flawed speculation, leading us to conclude that it is legitimate.
Therefore,
Fail to reject the null hypothesis. The P-value is greater than the level of significance.
The p-value associated with the null hypothesis = 0.05
To learn more about Null Hypothesis visit :
brainly.com/question/16261813
#SPJ4
what is the square root of -1?
Answers
Answer:
It might be weird but i is the answer and I don't know why exactly.
Step-by-step explanation:
I think it's because there is no real number when having a negative square.
10
Select the correct answer
What is the factored form of 1.458x^3 - 27

Answers
Answer:
answer D is correct maybe that help
All I need is help on these two so plz help me finish !!


Answers
Answer:5.86 9.26
Step-by-step explanation:
Answer:
For the first one it's 53 small cubes can fit in the right rectangle prism. For the second one the answer is A=120
lou gehrig's disease is autosomal recessive disease. if a woman and her husband are both carriers, what is the probability that their first child will be a phenotypically normal girl?
Answers
The probability that their first child will be a phenotypically normal girl is 3/8 or 37.5%.
Lou Gehrig's disease, also known as amyotrophic lateral sclerosis (ALS), is typically considered as an autosomal recessive disease. This means that both copies of the gene responsible for the disease need to be inherited, one from each parent, in order for an individual to be affected by the disease.
Given that the woman and her husband are both carriers of the disease, they each have one copy of the mutated gene and one normal gene. The probability of passing on the mutated gene to their child is 1/2 for each parent since they are carriers.
To determine the probability of their first child being a phenotypically normal girl, we need to consider the inheritance pattern. Let's break it down:
Gender: The probability of having a girl is 1/2, as gender is determined by the combination of the father's sperm (containing either an X or a Y chromosome) and the mother's egg (containing an X chromosome).
Phenotypically normal: For the child to be phenotypically normal, they should inherit at least one normal gene from either parent. The probability of inheriting a normal gene from the mother is 1/2, and the same probability applies for inheriting a normal gene from the father.
Independence: The probability of having a girl and inheriting a normal gene are independent events, so we can multiply their individual probabilities to calculate the combined probability.
Therefore, the probability of having a phenotypically normal girl is:
Probability of being a girl × Probability of inheriting a normal gene
= (1/2) × (1/2)
= 1/4
However, we also need to consider the possibility of having a boy. The probability of having a phenotypically normal boy is also 1/4.
Adding the probabilities of having a phenotypically normal girl and a phenotypically normal boy, we get:
1/4 + 1/4 = 2/4 = 1/2
Since the question specifically asks for the probability of having a phenotypically normal girl, we divide the probability of a phenotypically normal girl by the total probability of having a child:
(1/4) / (1/2) = 1/4 * 2/1 = 1/2 = 2/4 = 1/2
Therefore, the probability that their first child will be a phenotypically normal girl is 1/2 or 50%.
Visit here to learn more about probability:
brainly.com/question/32117953
#SPJ11